初中数学人教版八年级上册13.2.2 用坐标表示轴对称 说课课件(共35张PPT)
文档属性
| 名称 | 初中数学人教版八年级上册13.2.2 用坐标表示轴对称 说课课件(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 00:00:00 | ||
图片预览





文档简介
(共35张PPT)
用坐标表示轴对称
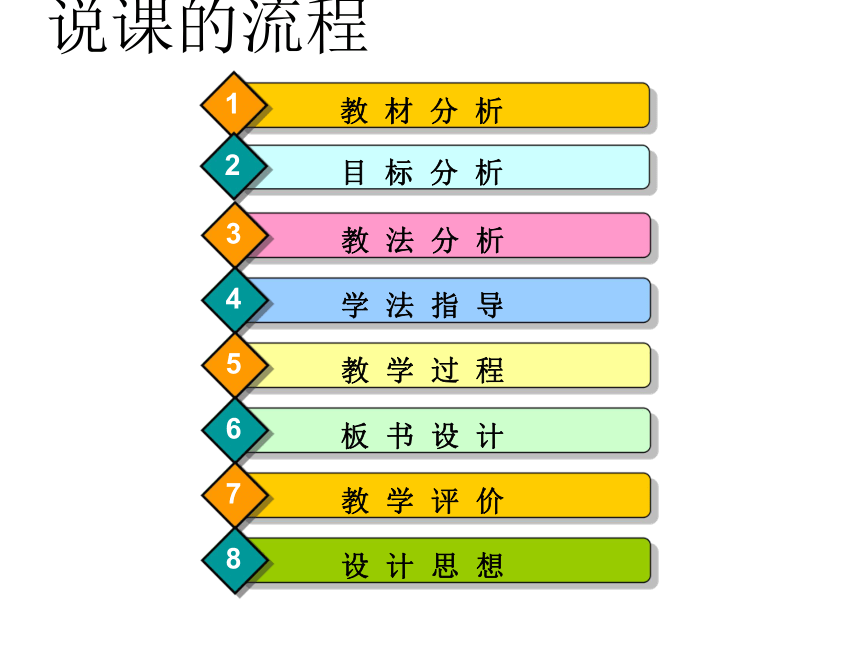
说课的流程
教 材 分 析
1
目 标 分 析
2
教 法 分 析
3
学 法 指 导
4
教 学 过 程
5
板 书 设 计
6
教 学 评 价
7
设 计 思 想
8
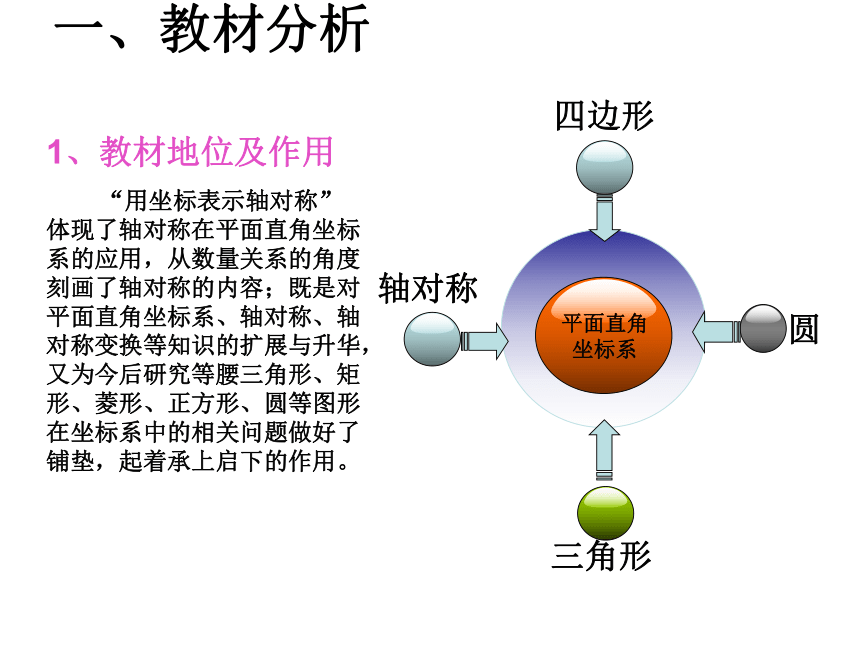
圆
平面直角
坐标系
四边形
轴对称
三角形
一、教材分析
1、教材地位及作用
“用坐标表示轴对称”体现了轴对称在平面直角坐标系的应用,从数量关系的角度刻画了轴对称的内容;既是对平面直角坐标系、轴对称、轴对称变换等知识的扩展与升华,又为今后研究等腰三角形、矩形、菱形、正方形、圆等图形在坐标系中的相关问题做好了铺垫,起着承上启下的作用。
一、教材分析
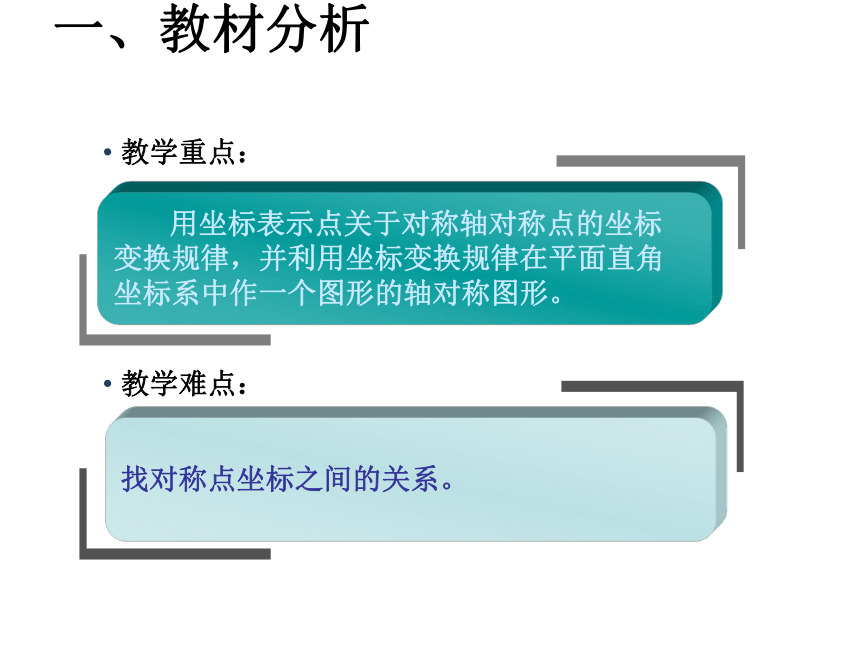
教学重点:
教学难点:
用坐标表示点关于对称轴对称点的坐标
变换规律,并利用坐标变换规律在平面直角
坐标系中作一个图形的轴对称图形。
找对称点坐标之间的关系。
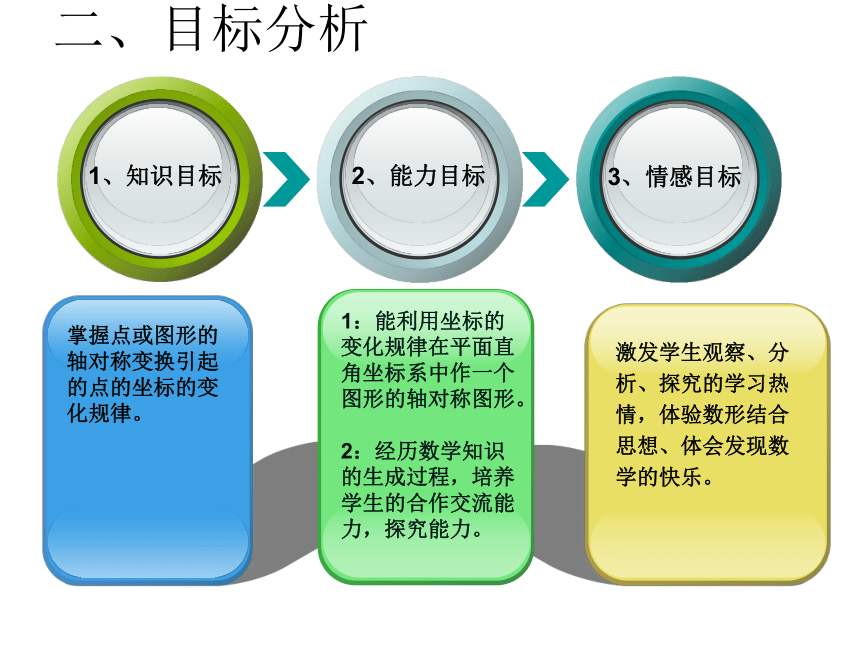
1、知识目标
2、能力目标
3、情感目标
二、目标分析
掌握点或图形的轴对称变换引起的点的坐标的变化规律。
激发学生观察、分析、探究的学习热情,体验数形结合思想、体会发现数学的快乐。
1:能利用坐标的变化规律在平面直角坐标系中作一个图形的轴对称图形。
2:经历数学知识的生成过程,培养学生的合作交流能力,探究能力。
三、教法分析
充分体现“以学生为主体,教师为主导”的教学原则
操
作
探
究
问题
驱动
探究
归纳
观察
思考
四、学法指导
8
作业布置,专题突破
7
归纳总结,形成系统
6
课堂测试,巩固提高
5
变式探究,层层递进
4
举例应用,加深认识
3
师生互动,探究新知
五、教学过程
教
学
流
程
图
1
创设情境、引入课题
2
回顾旧知,经典重现
1
创设情境、引入课题
1
创设情境、引入课题
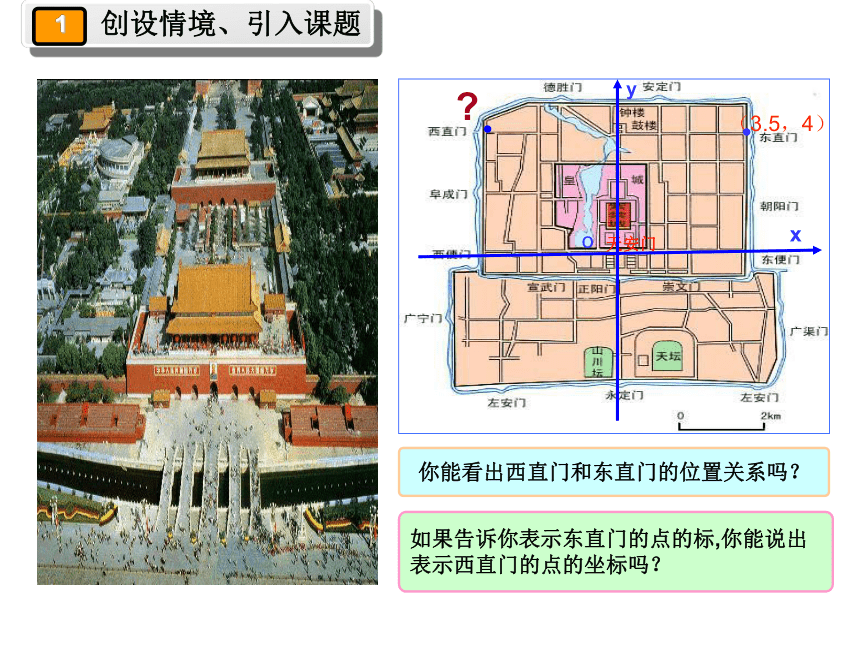
天安门
x
y
(3.5,4)
o
·
·
如果告诉你表示东直门的点的标,你能说出
表示西直门的点的坐标吗?
你能看出西直门和东直门的位置关系吗?
1
创设情境、引入课题
1
创设情境、引入课题
2
回顾旧知,经典重现
动动手画一画
已知点A和一条直线MN,你能画出
这个点关于已知直线的对称点吗 .
A
A’
M
N
O
∴ A ′就是点A关于直线MN的对称点。
过点A作AO⊥MN于O,然后延长AO至OA′,使AO=OA′.
探究1:在下图中,画出已知点关于X轴对称的点的坐标,并把坐
标填入表格中,
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B ′(-4, -2)
·
C ′(3, 4)
A (2,3)
·
A ′(2,-3)
·
已知点 关于X轴对称点
A (2,3)
B (-4, 2)
C (3, -4)
A’ 2, -3)
B’ ( -4, -2)
C’(3, 4)
关于x轴对称的点横坐标相同,纵坐标互为相反数.
3
师生互动,探究新知
x
y
探究1:在下图中,画出已知点关于X轴对称的点的坐标,并把坐
标填入表格中,
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B ′(4, 2)
·
C ′(-3, -4)
A (2,3)
·
A ′(-2,3)
·
已知点 关于Y轴对称点
A (2,3)
B (-4, 2)
C (3, -4)
A’ (-2, 3)
B’ ( 4, 2)
C’(-3, -4)
关于y 轴对称的点纵坐标相同,横坐标互为相反数.
3
师生互动,探究新知
x
y
探究结论
点(x, y)关于x轴对称的点的坐标为(x, -y)
点(x, y)关于y轴对称的点的坐标为(-x, y)
3
师生互动,探究新知
天安门
x
y
(3.5,4)
o
·
·
如果告诉你表示东直门的点的标,你能说出
表示西直门的点的坐标吗?
你能看出西直门和东直门的位置关系吗?
3
师生互动,探究新知
(-3.5,4)
1、点P(2,-4)关于x轴对称的点的坐标_____,关于y轴对称的点的坐标为_____.
2、已知点M(3,b)与点N(a,-3)关于x轴对称,则a=______, b=______
3、已知点P(3,x)与点Q(y,-3)关于y轴对称,则a=______, b=______
3
师生互动,探究新知
x
y
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
-5
-5
C
D
B
A
(-5,1)
(-2,1)
(-2,5)
(-5,4)
·
·
·
·
归纳:对于这类问题,关键要先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并顺次连接这些点,就可以得到这个图形的轴对称图形.
例题:四边形ABCD的四个顶点的坐标分别为A(-5,1)、B(-2,1)、
C(-2,5) 、D(-5,4),分别作出四边形关于x轴与y轴对称的图形。
4
举例应用,加深认识
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x=0
·
·
·
·
·
·
P(-2,3)
M(-1,1)
N’(3,-2)
N(-3,-2)
M’(-1,1)
P’(2,3)
x
y
纵坐标保持不变
1.如图,分别作出点P,M,N关于直线x=0(y轴)的对称点,你能发现它们坐标之间分别有什么关系吗
变式探究
5
变式探究,层层递进
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x=1
·
·
·
·
·
·
P(-2,3)
M(-1,1)
N’(5,-2)
N(-3,-2)
M’(3,1)
P’(4,3)
1.如图,分别作出点P,M,N关于直线x=1的对称点,你能发现它们坐标之间分别有什么关系吗
x
y
变式探究
纵坐标保持不变
x=
2x=x1+x2
5
变式探究,层层递进
y= -1
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
·
·
P(-2,3)
M(-1,1)
N’(-3,0)
N(-3,-2)
M’(-1,-3)
P’(-2,-5)
x
y
·
·
-5
1.如图,分别作出点P,M,N关于直线y=-1的对称点,你能发现它们坐标之间分别有什么关系吗
变式探究
横坐标保持不变
y=
2y=y1+y2
5
变式探究,层层递进
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x=1
·
·
·
·
·
·
P(-2,3)
M(-1,1)
N’(5,-2)
N(-3,-2)
M’(3,1)
P’(4,3)
x
y
y= -1
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
·
·
P(-2,3)
M(-1,1)
N’(-3,0)
N(-3,-2)
M’(-1,-3)
P’(-2,-5)
x
y
·
·
-5
5
变式探究,层层递进
第一关
太和殿
第二关
保和殿
第三关
乾清宫
第四关
坤宁宫
第五关
御花园
6
课堂测试,巩固提高
1.点A(3,7)关于x轴对称的点的坐标为 _______,关于y轴对称的点的坐标
为 _______.
2.已知点A(3,b)与点B(a,-3)关于x轴对称,则a+b=________.
3.点M(-4,0)关于y轴对称的点N的坐标
是_______,则MN的长为_______.
6
课堂测试,巩固提高
第一关:太和殿
4. 若点C(-2,-3)关于x轴的对称点为A,关于y轴的对称点为B,则△ABC的面积为 。
6
课堂测试,巩固提高
第二关:保和殿
5.当m 时,点P(2m+1,m-3)关于y轴的对称点在第四象限。
6
课堂测试,巩固提高
第三关:乾清宫
6.已知点A(a+2b,1),B(-2,2a-b)
(1)若点A,B关于x轴对称,求a、b的值
(2)若点A,B关于y轴对称,求a+b的值
6
课堂测试,巩固提高
第四关:坤宁宫
7. 思考:
(1)点(x,y)关于直线x=1对称点的坐标是多少 (2)点(x, y)关于直线x=-1对称点的坐标是多少 (3)点(x,y)关于直线y=1对称点的坐标是多少 (4)点(x,y)关于直线y=-1对称点的坐标是多少
6
课堂测试,巩固提高
第五关:御花园
1、我学会了:_____________________ 。
2 、我的疑惑是:_____________________ 。
这节课你有什么收获?还有什么疑惑吗?
丰收园
7
归纳总结,形成系统
1、必做题:课本第45--46页,第2、3、4题
2、选做题
如图,分别作点A(-3,0),B(-2,2)关于直线x=2的对称点A′、B′.
(1)求点A′、B′的坐标;
(2)求四边形ABB′A′的面积.
课
堂
内
外
8
作业布置,专题突破
§13.2.2 用坐标表示轴对称
例题1、-------------------------------
用坐标表示轴对称的点的坐标规律:
1:点(x,y)关于x轴对称的点的坐标
为(x,-y)
2:点(x,y)关于y轴对称的点的坐标
为(-x,y)
课堂练习区
六、板书设计
本节课能遵循教学规律,结合学生的认知特点,通过流畅、有层次的教学过程突出教学重点和难点,使学生在自主活动、主动探索以及合作交流的过程中获得了新知识,能力得到了提高。在相对轻松、有趣的探究活动中理解坐标思想,让学生由学会变为会学。
七、教学评价
以全面实施素质教育为指导思想,以“用坐标表示轴对称”知识为载体,以观察、探究、归纳的思维为主线,充分利用现代教育技术,让学生自觉主动地探究新知识。使教学不仅是传授知识的教学,更是一种开发思维,培养创新能力的教学。
八、设计思想
说课者:
用坐标表示轴对称
说课的流程
教 材 分 析
1
目 标 分 析
2
教 法 分 析
3
学 法 指 导
4
教 学 过 程
5
板 书 设 计
6
教 学 评 价
7
设 计 思 想
8
圆
平面直角
坐标系
四边形
轴对称
三角形
一、教材分析
1、教材地位及作用
“用坐标表示轴对称”体现了轴对称在平面直角坐标系的应用,从数量关系的角度刻画了轴对称的内容;既是对平面直角坐标系、轴对称、轴对称变换等知识的扩展与升华,又为今后研究等腰三角形、矩形、菱形、正方形、圆等图形在坐标系中的相关问题做好了铺垫,起着承上启下的作用。
一、教材分析
教学重点:
教学难点:
用坐标表示点关于对称轴对称点的坐标
变换规律,并利用坐标变换规律在平面直角
坐标系中作一个图形的轴对称图形。
找对称点坐标之间的关系。
1、知识目标
2、能力目标
3、情感目标
二、目标分析
掌握点或图形的轴对称变换引起的点的坐标的变化规律。
激发学生观察、分析、探究的学习热情,体验数形结合思想、体会发现数学的快乐。
1:能利用坐标的变化规律在平面直角坐标系中作一个图形的轴对称图形。
2:经历数学知识的生成过程,培养学生的合作交流能力,探究能力。
三、教法分析
充分体现“以学生为主体,教师为主导”的教学原则
操
作
探
究
问题
驱动
探究
归纳
观察
思考
四、学法指导
8
作业布置,专题突破
7
归纳总结,形成系统
6
课堂测试,巩固提高
5
变式探究,层层递进
4
举例应用,加深认识
3
师生互动,探究新知
五、教学过程
教
学
流
程
图
1
创设情境、引入课题
2
回顾旧知,经典重现
1
创设情境、引入课题
1
创设情境、引入课题
天安门
x
y
(3.5,4)
o
·
·
如果告诉你表示东直门的点的标,你能说出
表示西直门的点的坐标吗?
你能看出西直门和东直门的位置关系吗?
1
创设情境、引入课题
1
创设情境、引入课题
2
回顾旧知,经典重现
动动手画一画
已知点A和一条直线MN,你能画出
这个点关于已知直线的对称点吗 .
A
A’
M
N
O
∴ A ′就是点A关于直线MN的对称点。
过点A作AO⊥MN于O,然后延长AO至OA′,使AO=OA′.
探究1:在下图中,画出已知点关于X轴对称的点的坐标,并把坐
标填入表格中,
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B ′(-4, -2)
·
C ′(3, 4)
A (2,3)
·
A ′(2,-3)
·
已知点 关于X轴对称点
A (2,3)
B (-4, 2)
C (3, -4)
A’ 2, -3)
B’ ( -4, -2)
C’(3, 4)
关于x轴对称的点横坐标相同,纵坐标互为相反数.
3
师生互动,探究新知
x
y
探究1:在下图中,画出已知点关于X轴对称的点的坐标,并把坐
标填入表格中,
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B ′(4, 2)
·
C ′(-3, -4)
A (2,3)
·
A ′(-2,3)
·
已知点 关于Y轴对称点
A (2,3)
B (-4, 2)
C (3, -4)
A’ (-2, 3)
B’ ( 4, 2)
C’(-3, -4)
关于y 轴对称的点纵坐标相同,横坐标互为相反数.
3
师生互动,探究新知
x
y
探究结论
点(x, y)关于x轴对称的点的坐标为(x, -y)
点(x, y)关于y轴对称的点的坐标为(-x, y)
3
师生互动,探究新知
天安门
x
y
(3.5,4)
o
·
·
如果告诉你表示东直门的点的标,你能说出
表示西直门的点的坐标吗?
你能看出西直门和东直门的位置关系吗?
3
师生互动,探究新知
(-3.5,4)
1、点P(2,-4)关于x轴对称的点的坐标_____,关于y轴对称的点的坐标为_____.
2、已知点M(3,b)与点N(a,-3)关于x轴对称,则a=______, b=______
3、已知点P(3,x)与点Q(y,-3)关于y轴对称,则a=______, b=______
3
师生互动,探究新知
x
y
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
-5
-5
C
D
B
A
(-5,1)
(-2,1)
(-2,5)
(-5,4)
·
·
·
·
归纳:对于这类问题,关键要先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并顺次连接这些点,就可以得到这个图形的轴对称图形.
例题:四边形ABCD的四个顶点的坐标分别为A(-5,1)、B(-2,1)、
C(-2,5) 、D(-5,4),分别作出四边形关于x轴与y轴对称的图形。
4
举例应用,加深认识
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x=0
·
·
·
·
·
·
P(-2,3)
M(-1,1)
N’(3,-2)
N(-3,-2)
M’(-1,1)
P’(2,3)
x
y
纵坐标保持不变
1.如图,分别作出点P,M,N关于直线x=0(y轴)的对称点,你能发现它们坐标之间分别有什么关系吗
变式探究
5
变式探究,层层递进
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x=1
·
·
·
·
·
·
P(-2,3)
M(-1,1)
N’(5,-2)
N(-3,-2)
M’(3,1)
P’(4,3)
1.如图,分别作出点P,M,N关于直线x=1的对称点,你能发现它们坐标之间分别有什么关系吗
x
y
变式探究
纵坐标保持不变
x=
2x=x1+x2
5
变式探究,层层递进
y= -1
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
·
·
P(-2,3)
M(-1,1)
N’(-3,0)
N(-3,-2)
M’(-1,-3)
P’(-2,-5)
x
y
·
·
-5
1.如图,分别作出点P,M,N关于直线y=-1的对称点,你能发现它们坐标之间分别有什么关系吗
变式探究
横坐标保持不变
y=
2y=y1+y2
5
变式探究,层层递进
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x=1
·
·
·
·
·
·
P(-2,3)
M(-1,1)
N’(5,-2)
N(-3,-2)
M’(3,1)
P’(4,3)
x
y
y= -1
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
·
·
P(-2,3)
M(-1,1)
N’(-3,0)
N(-3,-2)
M’(-1,-3)
P’(-2,-5)
x
y
·
·
-5
5
变式探究,层层递进
第一关
太和殿
第二关
保和殿
第三关
乾清宫
第四关
坤宁宫
第五关
御花园
6
课堂测试,巩固提高
1.点A(3,7)关于x轴对称的点的坐标为 _______,关于y轴对称的点的坐标
为 _______.
2.已知点A(3,b)与点B(a,-3)关于x轴对称,则a+b=________.
3.点M(-4,0)关于y轴对称的点N的坐标
是_______,则MN的长为_______.
6
课堂测试,巩固提高
第一关:太和殿
4. 若点C(-2,-3)关于x轴的对称点为A,关于y轴的对称点为B,则△ABC的面积为 。
6
课堂测试,巩固提高
第二关:保和殿
5.当m 时,点P(2m+1,m-3)关于y轴的对称点在第四象限。
6
课堂测试,巩固提高
第三关:乾清宫
6.已知点A(a+2b,1),B(-2,2a-b)
(1)若点A,B关于x轴对称,求a、b的值
(2)若点A,B关于y轴对称,求a+b的值
6
课堂测试,巩固提高
第四关:坤宁宫
7. 思考:
(1)点(x,y)关于直线x=1对称点的坐标是多少 (2)点(x, y)关于直线x=-1对称点的坐标是多少 (3)点(x,y)关于直线y=1对称点的坐标是多少 (4)点(x,y)关于直线y=-1对称点的坐标是多少
6
课堂测试,巩固提高
第五关:御花园
1、我学会了:_____________________ 。
2 、我的疑惑是:_____________________ 。
这节课你有什么收获?还有什么疑惑吗?
丰收园
7
归纳总结,形成系统
1、必做题:课本第45--46页,第2、3、4题
2、选做题
如图,分别作点A(-3,0),B(-2,2)关于直线x=2的对称点A′、B′.
(1)求点A′、B′的坐标;
(2)求四边形ABB′A′的面积.
课
堂
内
外
8
作业布置,专题突破
§13.2.2 用坐标表示轴对称
例题1、-------------------------------
用坐标表示轴对称的点的坐标规律:
1:点(x,y)关于x轴对称的点的坐标
为(x,-y)
2:点(x,y)关于y轴对称的点的坐标
为(-x,y)
课堂练习区
六、板书设计
本节课能遵循教学规律,结合学生的认知特点,通过流畅、有层次的教学过程突出教学重点和难点,使学生在自主活动、主动探索以及合作交流的过程中获得了新知识,能力得到了提高。在相对轻松、有趣的探究活动中理解坐标思想,让学生由学会变为会学。
七、教学评价
以全面实施素质教育为指导思想,以“用坐标表示轴对称”知识为载体,以观察、探究、归纳的思维为主线,充分利用现代教育技术,让学生自觉主动地探究新知识。使教学不仅是传授知识的教学,更是一种开发思维,培养创新能力的教学。
八、设计思想
说课者:
