15.1-15.2分式的性质和运算 学案 2023--2024学年人教版八年级数学上册
文档属性
| 名称 | 15.1-15.2分式的性质和运算 学案 2023--2024学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 159.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 13:50:24 | ||
图片预览

文档简介
分式的性质和运算
一、分式的概念和性质
1.分式的意义
形如(A,B为整式),其中B中含有字母的式子叫分式.
当分子为零且分母不为零时,分式的值为零,而当分母为零时,分式没有意义.
2.分式的性质
(1)分式的基本性质:==(其中M是不为零的整式).
(2)约分和通分
题型一:分式的概念
例1代数式,,,+b,中,哪些是分式?
练1.1(1) 和 统称为有理式;
(2)- ,1+,,,,,中有 个是分式.
题型二:分式有意义的条件
例2当x取何值时,下列式子有意义?
(1) , (2), (3) .
练2.1(1)若分式不论x取何值,分式都有意义,则m的取值范围是( )
A.m≥1 B. m>1 C.m<1 D.m≤1
(2)使代数式÷有意义的x的值是 .
(3)x 时,分式 意义.
题型三:分式的值为零
例3当取何值时,下列分式的值为零?
(1); (2) .
练3.1当x取何值时,下列分式的值为零?
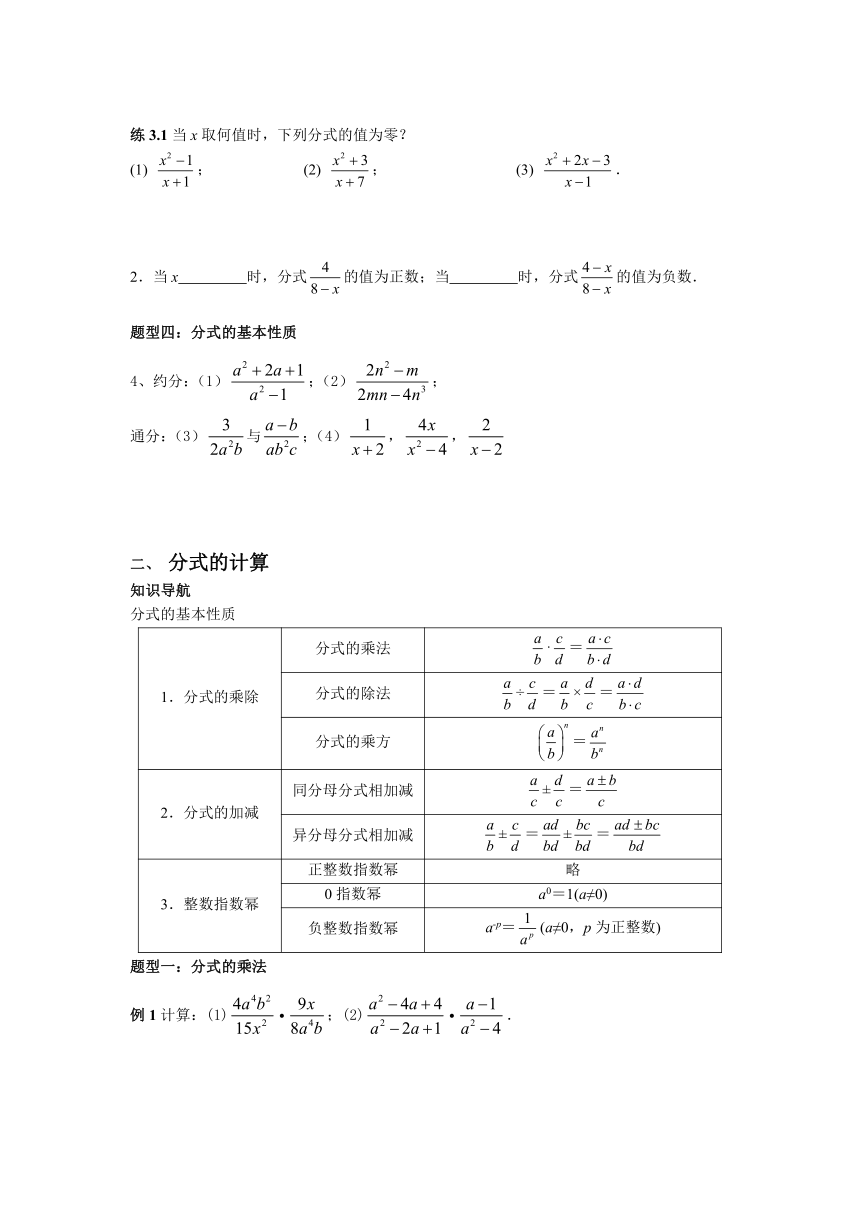
(1) ; (2) ; (3) .
当x 时,分式的值为正数;当 时,分式的值为负数.
题型四:分式的基本性质
4、约分:(1);(2);
通分:(3)与;(4),,
分式的计算
知识导航
分式的基本性质
1.分式的乘除 分式的乘法 ·=
分式的除法 ÷=×=
分式的乘方 =
2.分式的加减 同分母分式相加减 ±=
异分母分式相加减 ±=±=
3.整数指数幂 正整数指数幂 略
0指数幂 a0=1(a≠0)
负整数指数幂 a-p=(a≠0,p为正整数)
题型一:分式的乘法
例1计算:(1);(2).
练1计算.
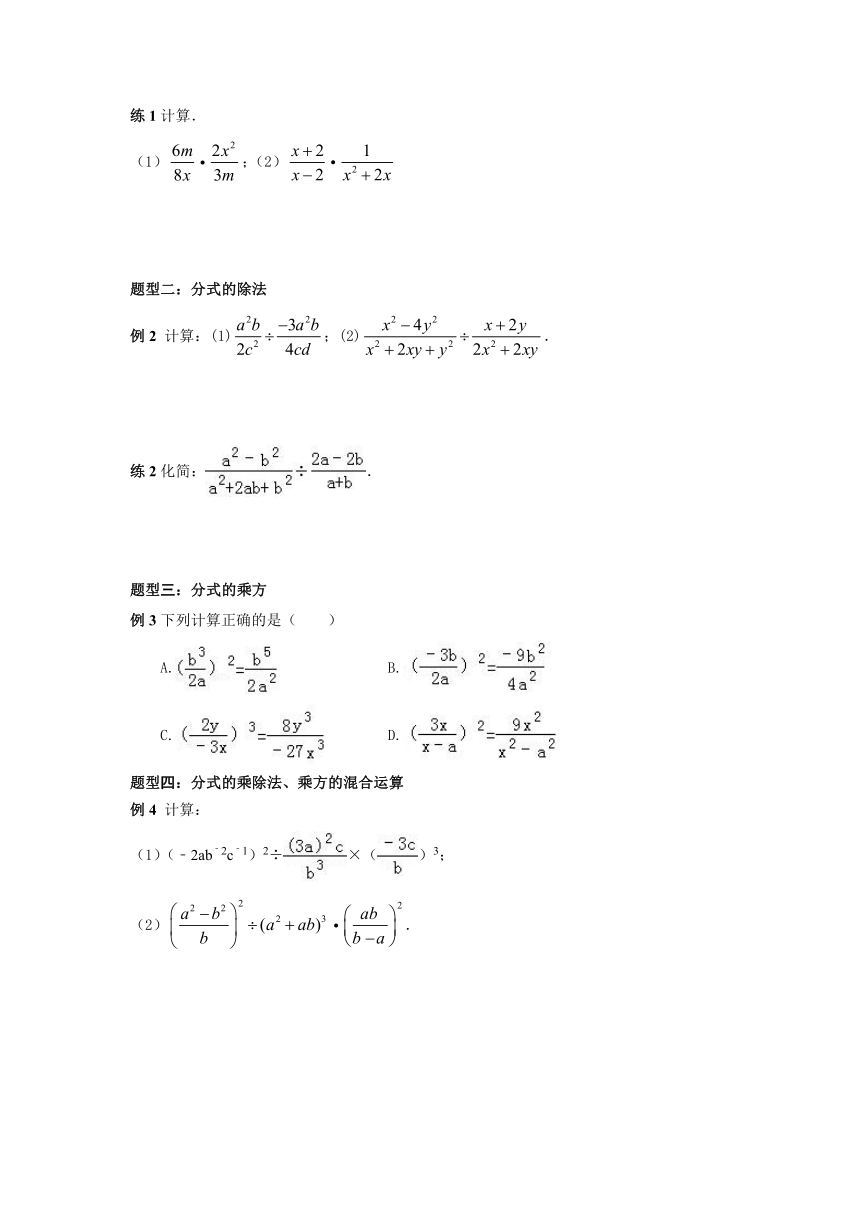
(1);(2)
题型二:分式的除法
例2 计算:(1);(2).
练2化简:.
题型三:分式的乘方
例3下列计算正确的是( )
A. B.
C. D.
题型四:分式的乘除法、乘方的混合运算
例4 计算:
(1)(﹣2ab﹣2c﹣1)2÷×()3;
(2).
练4计算:(1);
.
题型五:同分母分式的加减
例5计算:(1); (2);
(3); (4)
练5化简:
题型六:异分母分式的加减
例6计算:
(1);(2);(3).
练6计算:(1);(2).
题型七:分式的加减运算的应用
例7设A、B两地的距离为s,甲、乙两人同时从A地步行到B地,甲的速度为v,乙用v的速度行走了一半的距离,再用v的速度走完另一半的距离,那么谁先到达B地,说明理由.
【巩固练习】
一.选择题
1.的结果是( )
A. B. C. D.
2.化简的结果是( )
A.2 B. C. D.
3. 化简的结果是( )
A. B. C. D.1
4.化简,其结果是( )
A. B. C. D.
5.计算:,结果正确的是( )
A.2 B.1 C. D.
6.近似数0.33万表示为( )
A.3.3× B.3.3000× C.3.3× D.0.33×
二.填空题
7.计算的结果是______.
8.化简的结果是 .
9. ______,=______.
10. =______(≠0),______,______.
11. =______,=______.
12.环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为 .
三.解答题
13.化简:÷(1﹣)
14.计算下列各式,并把结果化成只含有正整数指数幂的形式:
(1) (2)
(3)
一、分式的概念和性质
1.分式的意义
形如(A,B为整式),其中B中含有字母的式子叫分式.
当分子为零且分母不为零时,分式的值为零,而当分母为零时,分式没有意义.
2.分式的性质
(1)分式的基本性质:==(其中M是不为零的整式).
(2)约分和通分
题型一:分式的概念
例1代数式,,,+b,中,哪些是分式?
练1.1(1) 和 统称为有理式;
(2)- ,1+,,,,,中有 个是分式.
题型二:分式有意义的条件
例2当x取何值时,下列式子有意义?
(1) , (2), (3) .
练2.1(1)若分式不论x取何值,分式都有意义,则m的取值范围是( )
A.m≥1 B. m>1 C.m<1 D.m≤1
(2)使代数式÷有意义的x的值是 .
(3)x 时,分式 意义.
题型三:分式的值为零
例3当取何值时,下列分式的值为零?
(1); (2) .
练3.1当x取何值时,下列分式的值为零?
(1) ; (2) ; (3) .
当x 时,分式的值为正数;当 时,分式的值为负数.
题型四:分式的基本性质
4、约分:(1);(2);
通分:(3)与;(4),,
分式的计算
知识导航
分式的基本性质
1.分式的乘除 分式的乘法 ·=
分式的除法 ÷=×=
分式的乘方 =
2.分式的加减 同分母分式相加减 ±=
异分母分式相加减 ±=±=
3.整数指数幂 正整数指数幂 略
0指数幂 a0=1(a≠0)
负整数指数幂 a-p=(a≠0,p为正整数)
题型一:分式的乘法
例1计算:(1);(2).
练1计算.
(1);(2)
题型二:分式的除法
例2 计算:(1);(2).
练2化简:.
题型三:分式的乘方
例3下列计算正确的是( )
A. B.
C. D.
题型四:分式的乘除法、乘方的混合运算
例4 计算:
(1)(﹣2ab﹣2c﹣1)2÷×()3;
(2).
练4计算:(1);
.
题型五:同分母分式的加减
例5计算:(1); (2);
(3); (4)
练5化简:
题型六:异分母分式的加减
例6计算:
(1);(2);(3).
练6计算:(1);(2).
题型七:分式的加减运算的应用
例7设A、B两地的距离为s,甲、乙两人同时从A地步行到B地,甲的速度为v,乙用v的速度行走了一半的距离,再用v的速度走完另一半的距离,那么谁先到达B地,说明理由.
【巩固练习】
一.选择题
1.的结果是( )
A. B. C. D.
2.化简的结果是( )
A.2 B. C. D.
3. 化简的结果是( )
A. B. C. D.1
4.化简,其结果是( )
A. B. C. D.
5.计算:,结果正确的是( )
A.2 B.1 C. D.
6.近似数0.33万表示为( )
A.3.3× B.3.3000× C.3.3× D.0.33×
二.填空题
7.计算的结果是______.
8.化简的结果是 .
9. ______,=______.
10. =______(≠0),______,______.
11. =______,=______.
12.环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为 .
三.解答题
13.化简:÷(1﹣)
14.计算下列各式,并把结果化成只含有正整数指数幂的形式:
(1) (2)
(3)
