2024年人教版中考数学微专题复习 尺规作图 课件(共49张PPT)
文档属性
| 名称 | 2024年人教版中考数学微专题复习 尺规作图 课件(共49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 13:28:34 | ||
图片预览





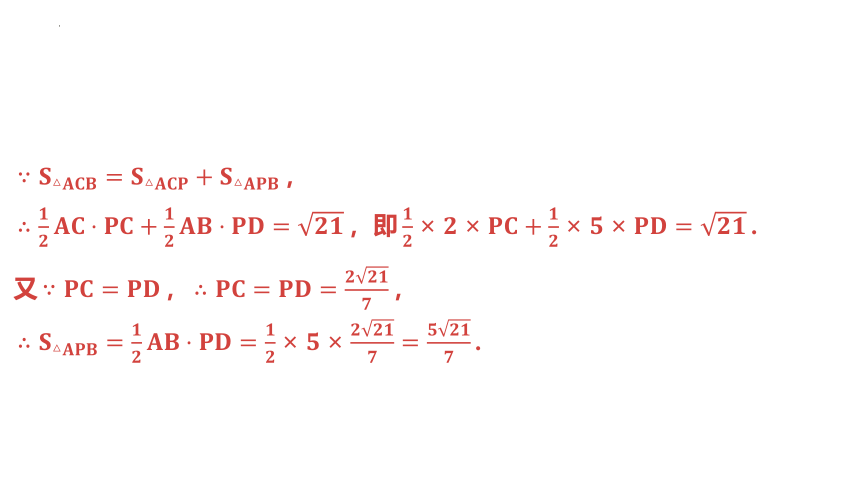


文档简介
(共49张PPT)
尺规作图
类型1 在几何图形中进行尺规作图
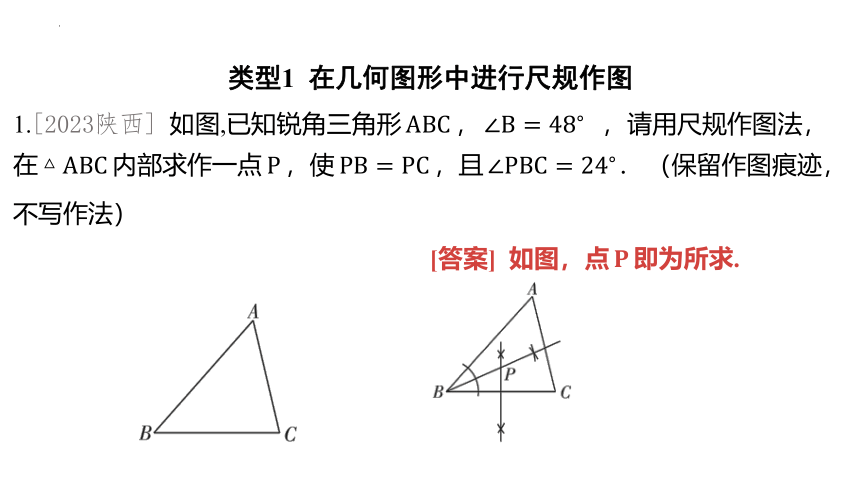
1.[2023陕西] 如图,已知锐角三角形 , ,请用尺规作图法,
在 内部求作一点 ,使 ,且 (保留作图痕迹,
不写作法)
[答案] 如图,点 即为所求.
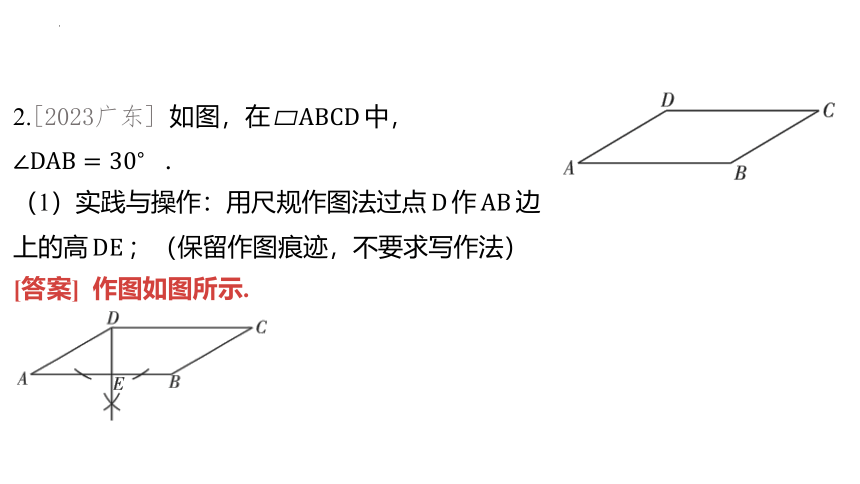
2.[2023广东] 如图,在 中,
.
(1)实践与操作:用尺规作图法过点 作 边
上的高 ;(保留作图痕迹,不要求写作法)
[答案] 作图如图所示.
(2)应用与计算:在(1)的条件下, , ,求 的长.
[答案] 在 中, , ,
,
.
3.[2023四川达州] 如图,在 中, , ,
.
(1)尺规作图:作 的平分线交 于点 (不写作法,保留作图痕迹);
[答案] 如图所示.
(2)在(1)所作图形中,求 的面积.
[答案] 如图,过点 作 于点 .
平分 , .
, , ,
,
.
,
,即 .
又 , ,
.
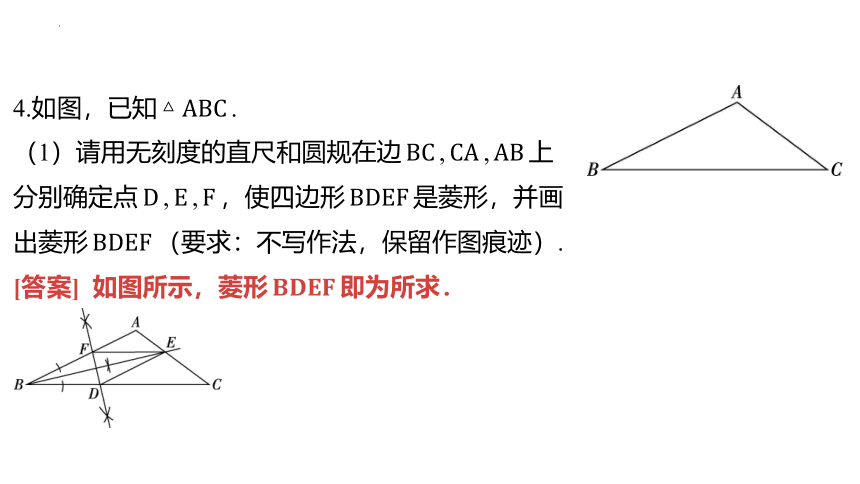
4.如图,已知 .
(1)请用无刻度的直尺和圆规在边 , , 上
分别确定点 , , ,使四边形 是菱形,并画
出菱形 (要求:不写作法,保留作图痕迹).
[答案] 如图所示,菱形 即为所求.
(2)若 , ,求(1)中所作菱形 的边长.
[答案] 四边形 是菱形, , ,
, .
设 ,则 ,
,解得 ,
中所作菱形 的边长为6.
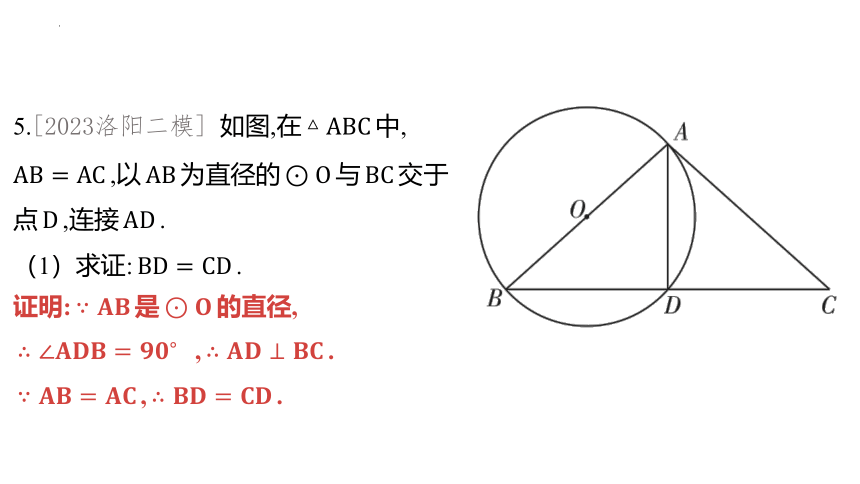
5.[2023洛阳二模] 如图,在 中,
,以 为直径的 与 交于
点 ,连接 .
(1)求证: .
证明: 是 的直径,
, .
, .
(2)若 与 相切,求 的度数.
[答案] 与 相切, .
又 , .
(3)用无刻度的直尺和圆规作出劣弧 的中点 .(不写作法,保留作图痕迹)
[答案] 如下图,点 就是所要作的 的中点.
法1
法2
法3
6.[2023郑州桐柏一中三模] 【材料】自从《义务教育数学课程标准(2022年
版)》实施以来,九年级的李老师通过查阅新课标获悉:切线长定理由“选
学”改为“必学”,并新增“会过圆外的一个点作圆的切线”.在学习完《切线的
性质与判定》后,她布置一题:“已知:如图所示, 及 外一点
.求作:直线 ,使 与 相切于点 .”李蕾同学经过探索,给出
了如下的一种作图方法:
①连接 ,分别以 , 为圆心,以大于 的长为半径作弧,两弧分别
交于 , 两点( , 分别位于直线 的上、下两侧);
②作直线 , 交 于点 ;
③以点 为圆心, 为半径作 , 交 于点 (点 位于直线
的上侧);
④连接 , 交 于点 ,则直线 即为所求.
(1)请按照步骤完成作图,并准确标注字母(尺规作图,保留作图痕迹);
[答案] 如图所示.
(2)结合图形,证明 是 的切线;
[答案] 由题意得, 为 的直径,
, .
为 的半径,
直线 为 的切线.
(3)若 的半径为2, ,依据作图痕迹求 的长.
[答案] 如图,连接 .
在 中, .
由图知 为 的垂直平分线, .
设 ,则 .
在 中, ,
,解得 ,
故 的长为 .
类型2 在函数图象中进行尺规作图
7.[2023洛阳三模] 如图,在平面直角坐标系中,一次函数
的图象与反比例函数 的图象
交于 , 两点(点 在点 左边),与 轴交于点 ,延
长 交反比例函数 的图象于点 .
(1)填空: _ __ (填“ ”“ ”或“ ”).
(2)请用无刻度的直尺和圆规作出 的平分线(要求:不写作法,保留作
图痕迹).
[答案] 如图(1)所示.
图(1)
(3)在 的平分线上取点 ,使 ,连接 ,当 时,
求 的面积.
图(2)
[答案] 如图(2),连接 ,
由 解得
点 在点 的左边, 点坐标为 .
当 时, , , ,
.
平分 , .
为 的中点, ,
, , , , .
8.[原创新题]如图,点 , 在反比例函数
的图象上, 轴于点 ,
轴于点 .已知 .
(1)若点 , 的横坐标相差1,纵坐标也相差1,求点 的坐标;
[答案] 由 ,可设 , .
由题意,得 , , , .
设点 , 的纵坐标分别为 , ,则 .
由题易得 , , ,
.
(2)请用无刻度的直尺和圆规作出过点 且垂直于 轴的垂线,垂足为点
(要求:不写作法,保留作图痕迹,使用 铅笔作图);
[答案] 作图如图(1)所示.
图(1)
(3)连接 ,若 , ,求 的值.
图(2)
[答案] 如图(2),设 与 交于点 ,
轴, 轴, 轴,
四边形 , 均是矩形,
, .
把 代入 ,得 ,
, .
, .
将 代入 ,得 ,
, .
在 中,由勾股定理,得 ,
即 ,解得 ,
易知 , .
9.如图,一次函数 的图象与反比例函数
的图象交于点 ,与反比例函数
的图象交于点 .连接 .
(1)求 , 的值.
[答案] 将 代入 ,得 , .
将 代入 ,
得 ,解得 ,
故一次函数的表达式为 .
将 代入 ,得 ,
.
将 代入 ,
得 ,解得 .
(2)请用无刻度的直尺和圆规作出线段 的垂直平分线 (要求:不写
作法,保留作图痕迹)
[答案] 如图(1),直线 即为所求.
图(1)
(3)求证: .
图(2)
证明:
方法一:如图(2),过点 作 轴于点 ,过
点 作 交 的延长线于点 ,
则 , , ,
,
, .
又 , ,
.
又 , ,
.
又 , .
方法二:连接 , , ,
, , ,
,
,即 .
又 , .
10.[原创新题]如图,一次函数 与反比例函数
的图象交于点 ,点 在 轴正半轴
上.
(1)求反比例函数的表达式.
[答案] 将 代入 ,得 , . 将 代入 ,
得 ,故反比例函数的表达式为 .
(2)请在 的内部作出满足下列条件的点 (尺规作图,不写作法,保留作图痕迹):
①点 到 两边的距离相等; .
[答案] 作图如图(1)所示.
图(1)
(3)请直接写出点 的坐标.
[答案] 点 的坐标是 .
图(2)
[解析] 解法提示:如图(2),延长 交 轴于点
,
则 轴, , ,
, ,
, .
类型3 在实际问题中进行尺规作图
11.如图,有一圆形破损盘子,已知圆弧上三点 , ,
,连接 , .
(1)请利用尺规,作出该盘子的圆心 ,并保留作图痕迹(不写作法).
[答案] 如图,点 即为所求.
(2)连接 ,若 是等腰三角形,且 , ,求该
盘子的半径 .
[答案] 如图,连接 交 于点 ,连接 ,则
,
,
,
.
在 中,根据勾股定理,得 ,
即 ,解得 .
12.如图(1)所示的拱桥为中承式钢筋砼 拱桥.桥的上部结构为2个钢
筋混凝土半月形拱肋,如图(2)是该桥拱肋的简化示意图,其中拱宽(弦 )
约100米.
(1)在图(2)中,请你用尺规作图的方法首先找出弧 所在圆的圆心 ,然
后确定弧 的中点 、弦 的中点 .(不要求写作法,但要保留作图痕迹)
[答案] 如图所示.
(2)在图(2)中,连接 , ,若 ,求该桥拱肋高 约为多
少米.(结果精确到0.1米.参考数据: , ,
)
[答案] 如图,由题可知 垂直平分 ,
米.
在 中, , ,
.
在 中, , ,
(米),
(米),
(米).
答:该桥拱肋高 约为18.6米.
13.[2023江苏徐州] 两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到:玉璧、玉环为我国的传统玉器,通常为正中带圆孔的扁圆形器物,据《尔雅·释器》记载:“肉倍好,谓之璧;肉好若一,谓之环.”如图(1),“肉”指边(阴影部分),“好”指孔,其比例关系见图示.以考古发现看,这两种玉器的“肉”与“好”未必符合该比例关系.
(1)若图(1)中两个大圆的直径相等,则璧与环的“肉”的面积之比为
_ ______.
[解析] 解法提示:设题图(1)中两个大圆的直径均为6.
易得璧中“肉”的面积为 ,
环中“肉”的面积为 ,
故璧和环中“肉”的面积之比为 .
(2)利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法).
①图(2)为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”.
[答案] 如图(1),用圆规比画可得 ,故该件玉器的比例关系符合
“肉好若一”.
图(1)
②图(3)表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
[答案] 如图(2)所示.
图(2)
尺规作图
类型1 在几何图形中进行尺规作图
1.[2023陕西] 如图,已知锐角三角形 , ,请用尺规作图法,
在 内部求作一点 ,使 ,且 (保留作图痕迹,
不写作法)
[答案] 如图,点 即为所求.
2.[2023广东] 如图,在 中,
.
(1)实践与操作:用尺规作图法过点 作 边
上的高 ;(保留作图痕迹,不要求写作法)
[答案] 作图如图所示.
(2)应用与计算:在(1)的条件下, , ,求 的长.
[答案] 在 中, , ,
,
.
3.[2023四川达州] 如图,在 中, , ,
.
(1)尺规作图:作 的平分线交 于点 (不写作法,保留作图痕迹);
[答案] 如图所示.
(2)在(1)所作图形中,求 的面积.
[答案] 如图,过点 作 于点 .
平分 , .
, , ,
,
.
,
,即 .
又 , ,
.
4.如图,已知 .
(1)请用无刻度的直尺和圆规在边 , , 上
分别确定点 , , ,使四边形 是菱形,并画
出菱形 (要求:不写作法,保留作图痕迹).
[答案] 如图所示,菱形 即为所求.
(2)若 , ,求(1)中所作菱形 的边长.
[答案] 四边形 是菱形, , ,
, .
设 ,则 ,
,解得 ,
中所作菱形 的边长为6.
5.[2023洛阳二模] 如图,在 中,
,以 为直径的 与 交于
点 ,连接 .
(1)求证: .
证明: 是 的直径,
, .
, .
(2)若 与 相切,求 的度数.
[答案] 与 相切, .
又 , .
(3)用无刻度的直尺和圆规作出劣弧 的中点 .(不写作法,保留作图痕迹)
[答案] 如下图,点 就是所要作的 的中点.
法1
法2
法3
6.[2023郑州桐柏一中三模] 【材料】自从《义务教育数学课程标准(2022年
版)》实施以来,九年级的李老师通过查阅新课标获悉:切线长定理由“选
学”改为“必学”,并新增“会过圆外的一个点作圆的切线”.在学习完《切线的
性质与判定》后,她布置一题:“已知:如图所示, 及 外一点
.求作:直线 ,使 与 相切于点 .”李蕾同学经过探索,给出
了如下的一种作图方法:
①连接 ,分别以 , 为圆心,以大于 的长为半径作弧,两弧分别
交于 , 两点( , 分别位于直线 的上、下两侧);
②作直线 , 交 于点 ;
③以点 为圆心, 为半径作 , 交 于点 (点 位于直线
的上侧);
④连接 , 交 于点 ,则直线 即为所求.
(1)请按照步骤完成作图,并准确标注字母(尺规作图,保留作图痕迹);
[答案] 如图所示.
(2)结合图形,证明 是 的切线;
[答案] 由题意得, 为 的直径,
, .
为 的半径,
直线 为 的切线.
(3)若 的半径为2, ,依据作图痕迹求 的长.
[答案] 如图,连接 .
在 中, .
由图知 为 的垂直平分线, .
设 ,则 .
在 中, ,
,解得 ,
故 的长为 .
类型2 在函数图象中进行尺规作图
7.[2023洛阳三模] 如图,在平面直角坐标系中,一次函数
的图象与反比例函数 的图象
交于 , 两点(点 在点 左边),与 轴交于点 ,延
长 交反比例函数 的图象于点 .
(1)填空: _ __ (填“ ”“ ”或“ ”).
(2)请用无刻度的直尺和圆规作出 的平分线(要求:不写作法,保留作
图痕迹).
[答案] 如图(1)所示.
图(1)
(3)在 的平分线上取点 ,使 ,连接 ,当 时,
求 的面积.
图(2)
[答案] 如图(2),连接 ,
由 解得
点 在点 的左边, 点坐标为 .
当 时, , , ,
.
平分 , .
为 的中点, ,
, , , , .
8.[原创新题]如图,点 , 在反比例函数
的图象上, 轴于点 ,
轴于点 .已知 .
(1)若点 , 的横坐标相差1,纵坐标也相差1,求点 的坐标;
[答案] 由 ,可设 , .
由题意,得 , , , .
设点 , 的纵坐标分别为 , ,则 .
由题易得 , , ,
.
(2)请用无刻度的直尺和圆规作出过点 且垂直于 轴的垂线,垂足为点
(要求:不写作法,保留作图痕迹,使用 铅笔作图);
[答案] 作图如图(1)所示.
图(1)
(3)连接 ,若 , ,求 的值.
图(2)
[答案] 如图(2),设 与 交于点 ,
轴, 轴, 轴,
四边形 , 均是矩形,
, .
把 代入 ,得 ,
, .
, .
将 代入 ,得 ,
, .
在 中,由勾股定理,得 ,
即 ,解得 ,
易知 , .
9.如图,一次函数 的图象与反比例函数
的图象交于点 ,与反比例函数
的图象交于点 .连接 .
(1)求 , 的值.
[答案] 将 代入 ,得 , .
将 代入 ,
得 ,解得 ,
故一次函数的表达式为 .
将 代入 ,得 ,
.
将 代入 ,
得 ,解得 .
(2)请用无刻度的直尺和圆规作出线段 的垂直平分线 (要求:不写
作法,保留作图痕迹)
[答案] 如图(1),直线 即为所求.
图(1)
(3)求证: .
图(2)
证明:
方法一:如图(2),过点 作 轴于点 ,过
点 作 交 的延长线于点 ,
则 , , ,
,
, .
又 , ,
.
又 , ,
.
又 , .
方法二:连接 , , ,
, , ,
,
,即 .
又 , .
10.[原创新题]如图,一次函数 与反比例函数
的图象交于点 ,点 在 轴正半轴
上.
(1)求反比例函数的表达式.
[答案] 将 代入 ,得 , . 将 代入 ,
得 ,故反比例函数的表达式为 .
(2)请在 的内部作出满足下列条件的点 (尺规作图,不写作法,保留作图痕迹):
①点 到 两边的距离相等; .
[答案] 作图如图(1)所示.
图(1)
(3)请直接写出点 的坐标.
[答案] 点 的坐标是 .
图(2)
[解析] 解法提示:如图(2),延长 交 轴于点
,
则 轴, , ,
, ,
, .
类型3 在实际问题中进行尺规作图
11.如图,有一圆形破损盘子,已知圆弧上三点 , ,
,连接 , .
(1)请利用尺规,作出该盘子的圆心 ,并保留作图痕迹(不写作法).
[答案] 如图,点 即为所求.
(2)连接 ,若 是等腰三角形,且 , ,求该
盘子的半径 .
[答案] 如图,连接 交 于点 ,连接 ,则
,
,
,
.
在 中,根据勾股定理,得 ,
即 ,解得 .
12.如图(1)所示的拱桥为中承式钢筋砼 拱桥.桥的上部结构为2个钢
筋混凝土半月形拱肋,如图(2)是该桥拱肋的简化示意图,其中拱宽(弦 )
约100米.
(1)在图(2)中,请你用尺规作图的方法首先找出弧 所在圆的圆心 ,然
后确定弧 的中点 、弦 的中点 .(不要求写作法,但要保留作图痕迹)
[答案] 如图所示.
(2)在图(2)中,连接 , ,若 ,求该桥拱肋高 约为多
少米.(结果精确到0.1米.参考数据: , ,
)
[答案] 如图,由题可知 垂直平分 ,
米.
在 中, , ,
.
在 中, , ,
(米),
(米),
(米).
答:该桥拱肋高 约为18.6米.
13.[2023江苏徐州] 两汉文化看徐州,桐桐在徐州博物馆“天工汉玉”展厅参观时了解到:玉璧、玉环为我国的传统玉器,通常为正中带圆孔的扁圆形器物,据《尔雅·释器》记载:“肉倍好,谓之璧;肉好若一,谓之环.”如图(1),“肉”指边(阴影部分),“好”指孔,其比例关系见图示.以考古发现看,这两种玉器的“肉”与“好”未必符合该比例关系.
(1)若图(1)中两个大圆的直径相等,则璧与环的“肉”的面积之比为
_ ______.
[解析] 解法提示:设题图(1)中两个大圆的直径均为6.
易得璧中“肉”的面积为 ,
环中“肉”的面积为 ,
故璧和环中“肉”的面积之比为 .
(2)利用圆规与无刻度的直尺,解决下列问题(保留作图痕迹,不写作法).
①图(2)为徐州狮子山楚王墓出土的“雷纹玉环”及其主视图,试判断该件玉器的比例关系是否符合“肉好若一”.
[答案] 如图(1),用圆规比画可得 ,故该件玉器的比例关系符合
“肉好若一”.
图(1)
②图(3)表示一件圆形玉坯,若将其加工成玉璧,且比例关系符合“肉倍好”,请画出内孔.
[答案] 如图(2)所示.
图(2)
同课章节目录
