2024年人教版中考数学微专题复习 规律探究题 课件(共29张PPT)
文档属性
| 名称 | 2024年人教版中考数学微专题复习 规律探究题 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 13:32:01 | ||
图片预览








文档简介
(共29张PPT)
规律探究题
类型1 数式或图形的规律探究
知识铺垫
解决数式或图形规律题的一般思路
1.标序号;
2.分析各式或图形中的“变”与“不变”的规律——重点分析“怎样变”,应结合各式或图形的序号进行前后对比分析;
3.猜想规律与“序号”之间的对应关系,并用关于“序号”的式子表示出来;
4.验证所归纳的结论,从而进行后续解答.
1.[2023山东济宁中考改编] 已知一列均不为1的数 , , , , ,
满足如下关系: , , , , .若
,则 的值是( )
B
A. B. C. D.2
2.[2023南阳宛城区一调改编] 观察下列等式: , ,
, , , , ,根据其中的规律
可得 的结果的个位数字是( )
B
A.0 B.1 C.7 D.8
3.[2023重庆B卷] 用圆圈按如图所示的规律拼图案,其中第①个图案中有2个
圆圈,第②个图案中有5个圆圈,第③个图案中有8个圆圈,第④个图案中有
11个圆圈……按此规律排列下去,则第⑦个图案中圆圈的个数为( )
B
A.14 B.20 C.23 D.26
4.[2023焦作二模改编] 如图,正方形 的边长为
1,以 为边作第2个正方形 ,再以 为边作
第3 个正方形 按照这样的规律作下去,
第2 024个正方形的面积为( )
C
A. B. C. D.
5.[2023湖南岳阳] 观察下列式子: , ,
, , , .依此规律,则第 (
为正整数)个等式是_ _________________.
6.[2023湖北恩施州] 观察下列两行数,探究第②行数与第①行数的关系:
,4, ,16, ,64, ①
0,7, ,21, ,71, ②
根据你的发现,完成填空:第①行数的第10个数为_______;取每行数的第2
023个数,则这两个数的和为_ _______________.
1 024
7.[2023湖北十堰] 用火柴棍拼成如图所示的图案,其中第①个图案由4个小等
边三角形围成1个小菱形,第②个图案由6个小等边三角形围成2个小菱形……
若按此规律拼下去,则第 个图案需要火柴棍的根数为________(用含 的式
子表示).
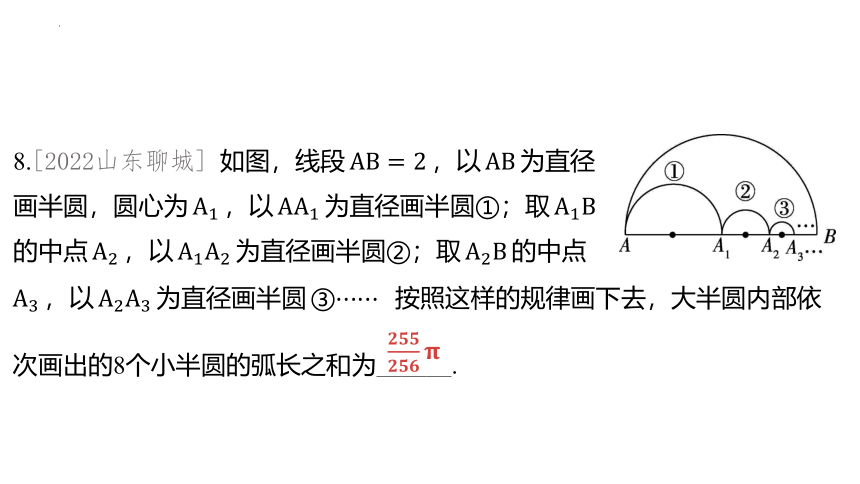
8.[2022山东聊城] 如图,线段 ,以 为直径
画半圆,圆心为 ,以 为直径画半圆①;取
的中点 ,以 为直径画半圆②;取 的中点
,以 为直径画半圆 按照这样的规律画下去,大半圆内部依
次画出的8个小半圆的弧长之和为_ _____.
类型2 平面直角坐标系中的规律探究
知识铺垫
解决平面直角坐标系中的规律探索题的一般步骤
第一步:分析图形的变化规律,根据图形的变化规律求出前面几个关键点的坐标.
第二步:通过分析变化规律得到一般规律(如点变换的循环规律或点运动的循环规律,点的横、纵坐标的变化规律等).
第三步:根据最后的变换次数或运动时间等,确定要求的点与哪个关键点重合,或要求的点与哪个关键点在同一象限内,或要求的点的横、纵坐标与哪个关键点的横、纵坐标相等,等等.
角度1 旋转型
(第9题)
9.如图,在平面直角坐标系中,半径为2的 与 轴的
正半轴交于点 .点 从点 出发,沿 按逆时针方向
运动,运动速度为每秒 个单位长度,则第2 024秒后点
的坐标为( )
B
A. B.
C. D.
(第10题)
10.[原创新题]如图,菱形 在平面直角坐标系
中的位置如图所示,其中 ,点 .
若将菱形 绕点 顺时针旋转,每秒旋转 ,
则第202秒时,点 的对应点的坐标为( )
B
A. B. ,
C. D.
(第11题)
11.如图,在平面直角坐标系中,点 在第一象限,点
到 轴的距离为4, ,点 为 轴上一点,且
,将 绕点 顺时针旋转,每秒旋转 ,
则第807秒时点 的坐标为( )
A
A. B.
C. D. ,
(第12题)
12.[2023洛阳二模改编] 如图,在 中,顶
点 在 轴的负半轴上, , ,
,将 绕点 逆时针旋转,每秒旋
转 ,则第2 024秒旋转结束时,点 的坐标为
( )
D
A. B.
C. D.
(第13题)
13.如图,在 中, ,
顶点 在第一象限,点 , 分别在 轴、
轴上, , , .将
绕点 顺时针旋转,每次旋转 ,
若旋转结束时,点 的对应点 的坐标是
,则旋转的次数可能是( )
C
A.2 022 B.2 023 C.2 024 D.2 025
(第14题)
14.[2023郑州二模改编] 如图,在平面直角坐标系中,
边长为2的等边三角形 在第二象限, 与 轴
重合,将 绕点 顺时针旋转 ,得到
,再作 关于原点 的中心对称图形,
得到 ,再将 绕点 顺时针旋转
B
A. B. C. D.
得到 ,再作 关于原点 的中心对称图形,得到 ,以此
类推,则点 的坐标是( )
15.[原创新题]如图,在平面直角坐标系中,正方形 的顶点
, .半圆与正方形 组成一个新的图形,点 为
(靠近点 )的三等分点,将此组合图形绕点 顺时针旋转,
每次旋转 ,则第102次旋转结束时,点 的对应点的坐标为
_ ____________.
角度2 平移或翻滚型
(第16题)
16.[2023驻马店二模] 如图,在平面直角坐标系中,点
为 轴上一点, ,以 为底构造等腰三角形
,且 ,将 沿着射线 方向平
移,每次平移的距离都等于线段 的长,则第70次平移
结束时,点 的对应点 的坐标为( )
C
A. B.
C. D.
(第17题)
17.如图,在平面直角坐标系中,正方形 的两
个顶点为 , ,规定把正方形
“先沿 轴翻折,再向下平移1个单位长度”为
一次变换,这样连续经过2 023次变换后,正方形
的中心的坐标为( )
C
A. B.
C. D.
18.如图,在 中, , , ,点 在 轴上.将
沿 轴正方向连续无滑动翻转100次,点 依次落在点 , , ,
, 处,则点 的坐标为_ ______.
19.如图,矩形 的顶点 , 在 轴的负半轴上,顶点 .
对角线 与 的交点为点 .将矩形 沿 轴向右滚动(无滑动),
使其一边保持落在 轴上,点 的对应点依次记为点 , , , ,
则点 的坐标为_ _________.
角度3 渐变型
20.[2023山东烟台] 如图,在直角坐标系中,每个网格小正方
形的边长均为1个单位长度,以点 为位似中心作正方形
,正方形 , ,按此规律作下去,所作正方
形的顶点均在格点上,其中正方形 的顶点坐标分别
A
A. B. C. D.
为 , , , ,则顶点 的坐标为( )
21.[2023山东枣庄] 如图,在反比例函数 的图象上有 ,
, , , 等点,它们的横坐标依次为1,2,3, , ,
分别过这些点作 轴与 轴的垂线,图中所构成的阴影部分的面积从左到右
依次为 , , , , ,则 _ _____.
22.[2023南阳宛城区二模改编] 如图,正方形 的中心与坐标原点 重
合,将顶点 绕点 逆时针旋转 得点 ,再将 绕点 逆
时针旋转 得点 ,再将 绕点 逆时针旋转 得点 ,再将 绕
点 逆时针旋转 得点 ,再将 绕点 逆时针旋转 得点
以此类推,则点 的坐标是_ _____________.
(第23题)
23.[2023山东东营中考改编] 如图,在平面直角坐标系
中,直线 与 轴交于点 ,以 为
边作正方形 ,点 在 轴上,延长 交直线
于点 ,以 为边作正方形 ,点 在 轴
上,以同样的方式依次作正方形 , ,正方
形 ,则点 的横坐标是
_ ____________.
(第24题)
24.[2023湖南怀化中考改编] 在平面直角坐标系
中, 为等边三角形,点 的坐标为 .
把 按如图所示的方式放置,并将 进
行变换:第一次变换将 绕着原点 顺时针旋
转 ,同时边长扩大为 边长的2倍,得到
;第二次旋转将 绕着原点 顺时针旋转 ,同时边长
扩大为 边长的2倍,得到 以此类推,得到
.则 的边长为_______,点 的坐标为
_ ___________________.
角度4 徘徊型
(第25题)
25.如图,四边形 是矩形, , ,
轴.点 从点 出发,沿 以每秒2个单位
长度的速度运动,当运动到第167秒时, 的长为( )
B
A.0 B.2 C.3 D.
(第26题)
26.[2023三门峡二模改编] 如图,菱形 的四个顶点均
在坐标轴上.已知 , , .点 是菱形
边上的一个动点,连接 ,把 绕着点 顺时针旋
转 得到 ,连接 .若点 从点 出发,以每秒5个
单位长度沿 方向运动,则第2 024秒时,
点 的坐标为( )
C
A. B. C. D.
27.[2023洛阳三模改编] 如图,在平面直角坐标系中,一动点从原点 出发,按
向上、向右、向下、向右的方向不断地移动,每次移动一个单位长度,得到点
, , , , ,那么点 的坐标为( )
A
A. B. C. D.
规律探究题
类型1 数式或图形的规律探究
知识铺垫
解决数式或图形规律题的一般思路
1.标序号;
2.分析各式或图形中的“变”与“不变”的规律——重点分析“怎样变”,应结合各式或图形的序号进行前后对比分析;
3.猜想规律与“序号”之间的对应关系,并用关于“序号”的式子表示出来;
4.验证所归纳的结论,从而进行后续解答.
1.[2023山东济宁中考改编] 已知一列均不为1的数 , , , , ,
满足如下关系: , , , , .若
,则 的值是( )
B
A. B. C. D.2
2.[2023南阳宛城区一调改编] 观察下列等式: , ,
, , , , ,根据其中的规律
可得 的结果的个位数字是( )
B
A.0 B.1 C.7 D.8
3.[2023重庆B卷] 用圆圈按如图所示的规律拼图案,其中第①个图案中有2个
圆圈,第②个图案中有5个圆圈,第③个图案中有8个圆圈,第④个图案中有
11个圆圈……按此规律排列下去,则第⑦个图案中圆圈的个数为( )
B
A.14 B.20 C.23 D.26
4.[2023焦作二模改编] 如图,正方形 的边长为
1,以 为边作第2个正方形 ,再以 为边作
第3 个正方形 按照这样的规律作下去,
第2 024个正方形的面积为( )
C
A. B. C. D.
5.[2023湖南岳阳] 观察下列式子: , ,
, , , .依此规律,则第 (
为正整数)个等式是_ _________________.
6.[2023湖北恩施州] 观察下列两行数,探究第②行数与第①行数的关系:
,4, ,16, ,64, ①
0,7, ,21, ,71, ②
根据你的发现,完成填空:第①行数的第10个数为_______;取每行数的第2
023个数,则这两个数的和为_ _______________.
1 024
7.[2023湖北十堰] 用火柴棍拼成如图所示的图案,其中第①个图案由4个小等
边三角形围成1个小菱形,第②个图案由6个小等边三角形围成2个小菱形……
若按此规律拼下去,则第 个图案需要火柴棍的根数为________(用含 的式
子表示).
8.[2022山东聊城] 如图,线段 ,以 为直径
画半圆,圆心为 ,以 为直径画半圆①;取
的中点 ,以 为直径画半圆②;取 的中点
,以 为直径画半圆 按照这样的规律画下去,大半圆内部依
次画出的8个小半圆的弧长之和为_ _____.
类型2 平面直角坐标系中的规律探究
知识铺垫
解决平面直角坐标系中的规律探索题的一般步骤
第一步:分析图形的变化规律,根据图形的变化规律求出前面几个关键点的坐标.
第二步:通过分析变化规律得到一般规律(如点变换的循环规律或点运动的循环规律,点的横、纵坐标的变化规律等).
第三步:根据最后的变换次数或运动时间等,确定要求的点与哪个关键点重合,或要求的点与哪个关键点在同一象限内,或要求的点的横、纵坐标与哪个关键点的横、纵坐标相等,等等.
角度1 旋转型
(第9题)
9.如图,在平面直角坐标系中,半径为2的 与 轴的
正半轴交于点 .点 从点 出发,沿 按逆时针方向
运动,运动速度为每秒 个单位长度,则第2 024秒后点
的坐标为( )
B
A. B.
C. D.
(第10题)
10.[原创新题]如图,菱形 在平面直角坐标系
中的位置如图所示,其中 ,点 .
若将菱形 绕点 顺时针旋转,每秒旋转 ,
则第202秒时,点 的对应点的坐标为( )
B
A. B. ,
C. D.
(第11题)
11.如图,在平面直角坐标系中,点 在第一象限,点
到 轴的距离为4, ,点 为 轴上一点,且
,将 绕点 顺时针旋转,每秒旋转 ,
则第807秒时点 的坐标为( )
A
A. B.
C. D. ,
(第12题)
12.[2023洛阳二模改编] 如图,在 中,顶
点 在 轴的负半轴上, , ,
,将 绕点 逆时针旋转,每秒旋
转 ,则第2 024秒旋转结束时,点 的坐标为
( )
D
A. B.
C. D.
(第13题)
13.如图,在 中, ,
顶点 在第一象限,点 , 分别在 轴、
轴上, , , .将
绕点 顺时针旋转,每次旋转 ,
若旋转结束时,点 的对应点 的坐标是
,则旋转的次数可能是( )
C
A.2 022 B.2 023 C.2 024 D.2 025
(第14题)
14.[2023郑州二模改编] 如图,在平面直角坐标系中,
边长为2的等边三角形 在第二象限, 与 轴
重合,将 绕点 顺时针旋转 ,得到
,再作 关于原点 的中心对称图形,
得到 ,再将 绕点 顺时针旋转
B
A. B. C. D.
得到 ,再作 关于原点 的中心对称图形,得到 ,以此
类推,则点 的坐标是( )
15.[原创新题]如图,在平面直角坐标系中,正方形 的顶点
, .半圆与正方形 组成一个新的图形,点 为
(靠近点 )的三等分点,将此组合图形绕点 顺时针旋转,
每次旋转 ,则第102次旋转结束时,点 的对应点的坐标为
_ ____________.
角度2 平移或翻滚型
(第16题)
16.[2023驻马店二模] 如图,在平面直角坐标系中,点
为 轴上一点, ,以 为底构造等腰三角形
,且 ,将 沿着射线 方向平
移,每次平移的距离都等于线段 的长,则第70次平移
结束时,点 的对应点 的坐标为( )
C
A. B.
C. D.
(第17题)
17.如图,在平面直角坐标系中,正方形 的两
个顶点为 , ,规定把正方形
“先沿 轴翻折,再向下平移1个单位长度”为
一次变换,这样连续经过2 023次变换后,正方形
的中心的坐标为( )
C
A. B.
C. D.
18.如图,在 中, , , ,点 在 轴上.将
沿 轴正方向连续无滑动翻转100次,点 依次落在点 , , ,
, 处,则点 的坐标为_ ______.
19.如图,矩形 的顶点 , 在 轴的负半轴上,顶点 .
对角线 与 的交点为点 .将矩形 沿 轴向右滚动(无滑动),
使其一边保持落在 轴上,点 的对应点依次记为点 , , , ,
则点 的坐标为_ _________.
角度3 渐变型
20.[2023山东烟台] 如图,在直角坐标系中,每个网格小正方
形的边长均为1个单位长度,以点 为位似中心作正方形
,正方形 , ,按此规律作下去,所作正方
形的顶点均在格点上,其中正方形 的顶点坐标分别
A
A. B. C. D.
为 , , , ,则顶点 的坐标为( )
21.[2023山东枣庄] 如图,在反比例函数 的图象上有 ,
, , , 等点,它们的横坐标依次为1,2,3, , ,
分别过这些点作 轴与 轴的垂线,图中所构成的阴影部分的面积从左到右
依次为 , , , , ,则 _ _____.
22.[2023南阳宛城区二模改编] 如图,正方形 的中心与坐标原点 重
合,将顶点 绕点 逆时针旋转 得点 ,再将 绕点 逆
时针旋转 得点 ,再将 绕点 逆时针旋转 得点 ,再将 绕
点 逆时针旋转 得点 ,再将 绕点 逆时针旋转 得点
以此类推,则点 的坐标是_ _____________.
(第23题)
23.[2023山东东营中考改编] 如图,在平面直角坐标系
中,直线 与 轴交于点 ,以 为
边作正方形 ,点 在 轴上,延长 交直线
于点 ,以 为边作正方形 ,点 在 轴
上,以同样的方式依次作正方形 , ,正方
形 ,则点 的横坐标是
_ ____________.
(第24题)
24.[2023湖南怀化中考改编] 在平面直角坐标系
中, 为等边三角形,点 的坐标为 .
把 按如图所示的方式放置,并将 进
行变换:第一次变换将 绕着原点 顺时针旋
转 ,同时边长扩大为 边长的2倍,得到
;第二次旋转将 绕着原点 顺时针旋转 ,同时边长
扩大为 边长的2倍,得到 以此类推,得到
.则 的边长为_______,点 的坐标为
_ ___________________.
角度4 徘徊型
(第25题)
25.如图,四边形 是矩形, , ,
轴.点 从点 出发,沿 以每秒2个单位
长度的速度运动,当运动到第167秒时, 的长为( )
B
A.0 B.2 C.3 D.
(第26题)
26.[2023三门峡二模改编] 如图,菱形 的四个顶点均
在坐标轴上.已知 , , .点 是菱形
边上的一个动点,连接 ,把 绕着点 顺时针旋
转 得到 ,连接 .若点 从点 出发,以每秒5个
单位长度沿 方向运动,则第2 024秒时,
点 的坐标为( )
C
A. B. C. D.
27.[2023洛阳三模改编] 如图,在平面直角坐标系中,一动点从原点 出发,按
向上、向右、向下、向右的方向不断地移动,每次移动一个单位长度,得到点
, , , , ,那么点 的坐标为( )
A
A. B. C. D.
同课章节目录
