八年级数学上册第12章《全等三角形》期末复习题 (1)(含答案)
文档属性
| 名称 | 八年级数学上册第12章《全等三角形》期末复习题 (1)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 140.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 13:36:48 | ||
图片预览



文档简介
第12章《全等三角形》期末复习题
一、选择题
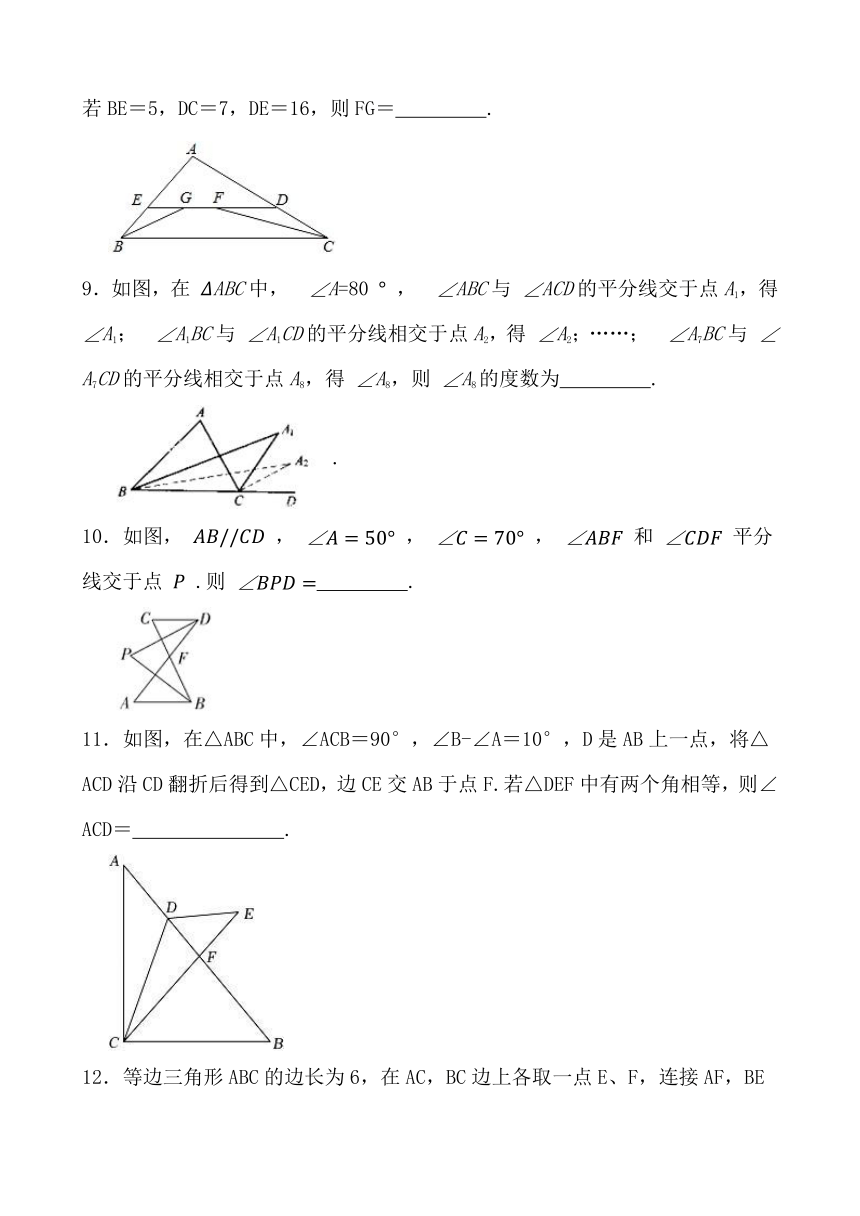
1.如图,已知∠CAB=∠DBA,那么还应添加一个条件,才能推出△ABC≌△BAD.则从下列条件中补充一个条件后,仍不能判定△ABC≌△BAD的是( )
A.∠C=∠D B.BC=AD
C.∠CBA=∠DAB D.AC=BD
2.以下四组图形中,与如下图形全等的是( )
A. B.
C. D.
3.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB,交AC于点E,ED=3,则AE的长为( )
A.1.5 B.2 C.3 D.3.5
4.如图,在 中, , 是 的中点,若 ,则 ( )
A.108° B.720° C.54° D.36°
5.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )
A.(S、S、S) B.(S、A、S)
C.(A、S、A) D.(A、A、S)
6.如图, , 和 , 和 为对应边,若 , ,则 等于( )
A. B. C. D.
二、填空题
7.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是 .
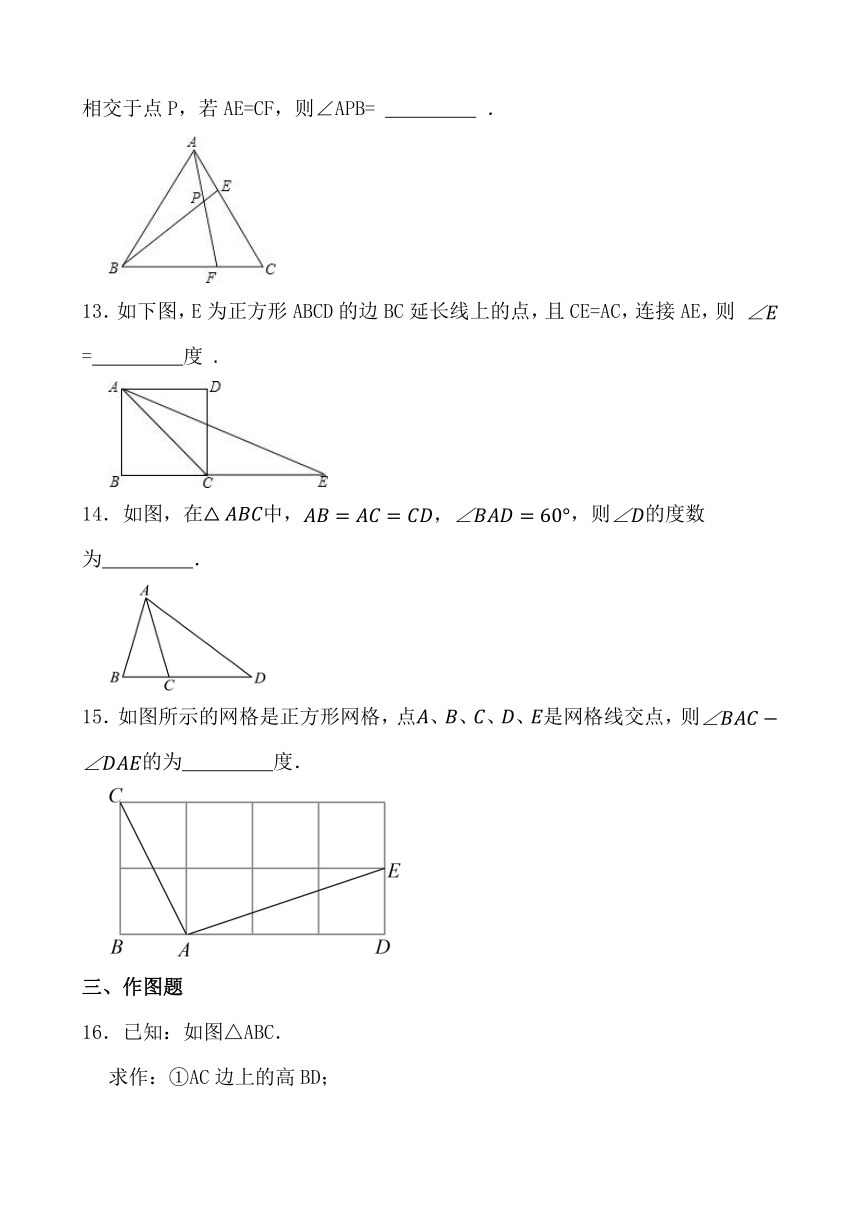
8.如图,在△ABC中,ED//BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若BE=5,DC=7,DE=16,则FG= .
9.如图,在 ABC中, A=80 , ABC与 ACD的平分线交于点A1,得 A1; A1BC与 A1CD的平分线相交于点A2,得 A2;……; A7BC与 A7CD的平分线相交于点A8,得 A8,则 A8的度数为 .
.
10.如图, , , , 和 平分线交于点 .则 .
11.如图,在△ABC中,∠ACB=90°,∠B-∠A=10°,D是AB上一点,将△ACD沿CD翻折后得到△CED,边CE交AB于点F.若△DEF中有两个角相等,则∠ACD= .
12.等边三角形ABC的边长为6,在AC,BC边上各取一点E、F,连接AF,BE相交于点P,若AE=CF,则∠APB= .
13.如下图,E为正方形ABCD的边BC延长线上的点,且CE=AC,连接AE,则 = 度
14.如图,在中,,则的度数为 .
15.如图所示的网格是正方形网格,点、、、、是网格线交点,则的为 度.
三、作图题
16.已知:如图△ABC.
求作:①AC边上的高BD;
②△ABC的角平分线CE.
四、解答题
17.如图所示,已知在中,,,直线m经过点A,,,垂足分别为D,E,求证:.
18. 如图,已知AC平分,于E,于F,且.
(1)求证:;
(2)若,,求DF的长.
19.已知:如图,在 中,D是BC的中点,点E、F分别在AB、AC上,且 , .求证: , .
20.如图,AC为矩形ABCD的对角线,DE⊥AC于E,BF⊥AC于F。
求证:DE=BF
21.如图,已知:∠1=∠2,∠C=∠D.求证:BC=BD.
22.如图,两根旗杆相距12m,某人从B点沿BA走向A点,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,求:这个人从B点到M点运动了多长时间?
答案解析部分
1.B
2.B
3.C
4.C
5.A
6.A
7.5
8.4
9.
10.60°
11.15°或30°
12.120°
13.
14.40°
15.45
16.解: 如图所示:
17.证明:∵ , ,
∴
,
∴ ,
,
∴ ,
在 和 中,
,
∴ ,
∴ , ,
∴ .
18.(1)证明:∵AC平分,于E,于F,∴,
在和中,,,
∴(HL).
(2)解:在和中,,
∵(HL),∴,
∵,∴,
∵,,∴,
∴,∴.
19.证明:∵D是BC的中点,
∴BD=DC,
∵ , .
∴∠EBD=∠FDC,∠EDB=∠C,
在△EBD和△FDC中
∴△EBD≌△FDC(ASA),
∴ , .
20.证明:由题知DC∥AB,
则∠DCA=∠BAC,
又DE⊥AC,BF⊥AC
∠DEC=∠BFA=90°,
又DC=BA,
可得△DEC≌△BFA,
则DE=BF,
得证
21.证明:在△ABC和△ABD中,
∴△ABC≌△ABD(AAS),
∴BC=BD.
22.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°
∴∠CMA+∠ACM=90°,
∴∠ACM=∠DMB,
在Rt△ACM和Rt△BMD中,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴AC=BM=3m,
∴他到达点M时,运动时间为3÷1=3(s).
答:这个人从B点到M点运动了3s.
一、选择题
1.如图,已知∠CAB=∠DBA,那么还应添加一个条件,才能推出△ABC≌△BAD.则从下列条件中补充一个条件后,仍不能判定△ABC≌△BAD的是( )
A.∠C=∠D B.BC=AD
C.∠CBA=∠DAB D.AC=BD
2.以下四组图形中,与如下图形全等的是( )
A. B.
C. D.
3.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB,交AC于点E,ED=3,则AE的长为( )
A.1.5 B.2 C.3 D.3.5
4.如图,在 中, , 是 的中点,若 ,则 ( )
A.108° B.720° C.54° D.36°
5.用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )
A.(S、S、S) B.(S、A、S)
C.(A、S、A) D.(A、A、S)
6.如图, , 和 , 和 为对应边,若 , ,则 等于( )
A. B. C. D.
二、填空题
7.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是 .
8.如图,在△ABC中,ED//BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若BE=5,DC=7,DE=16,则FG= .
9.如图,在 ABC中, A=80 , ABC与 ACD的平分线交于点A1,得 A1; A1BC与 A1CD的平分线相交于点A2,得 A2;……; A7BC与 A7CD的平分线相交于点A8,得 A8,则 A8的度数为 .
.
10.如图, , , , 和 平分线交于点 .则 .
11.如图,在△ABC中,∠ACB=90°,∠B-∠A=10°,D是AB上一点,将△ACD沿CD翻折后得到△CED,边CE交AB于点F.若△DEF中有两个角相等,则∠ACD= .
12.等边三角形ABC的边长为6,在AC,BC边上各取一点E、F,连接AF,BE相交于点P,若AE=CF,则∠APB= .
13.如下图,E为正方形ABCD的边BC延长线上的点,且CE=AC,连接AE,则 = 度
14.如图,在中,,则的度数为 .
15.如图所示的网格是正方形网格,点、、、、是网格线交点,则的为 度.
三、作图题
16.已知:如图△ABC.
求作:①AC边上的高BD;
②△ABC的角平分线CE.
四、解答题
17.如图所示,已知在中,,,直线m经过点A,,,垂足分别为D,E,求证:.
18. 如图,已知AC平分,于E,于F,且.
(1)求证:;
(2)若,,求DF的长.
19.已知:如图,在 中,D是BC的中点,点E、F分别在AB、AC上,且 , .求证: , .
20.如图,AC为矩形ABCD的对角线,DE⊥AC于E,BF⊥AC于F。
求证:DE=BF
21.如图,已知:∠1=∠2,∠C=∠D.求证:BC=BD.
22.如图,两根旗杆相距12m,某人从B点沿BA走向A点,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,求:这个人从B点到M点运动了多长时间?
答案解析部分
1.B
2.B
3.C
4.C
5.A
6.A
7.5
8.4
9.
10.60°
11.15°或30°
12.120°
13.
14.40°
15.45
16.解: 如图所示:
17.证明:∵ , ,
∴
,
∴ ,
,
∴ ,
在 和 中,
,
∴ ,
∴ , ,
∴ .
18.(1)证明:∵AC平分,于E,于F,∴,
在和中,,,
∴(HL).
(2)解:在和中,,
∵(HL),∴,
∵,∴,
∵,,∴,
∴,∴.
19.证明:∵D是BC的中点,
∴BD=DC,
∵ , .
∴∠EBD=∠FDC,∠EDB=∠C,
在△EBD和△FDC中
∴△EBD≌△FDC(ASA),
∴ , .
20.证明:由题知DC∥AB,
则∠DCA=∠BAC,
又DE⊥AC,BF⊥AC
∠DEC=∠BFA=90°,
又DC=BA,
可得△DEC≌△BFA,
则DE=BF,
得证
21.证明:在△ABC和△ABD中,
∴△ABC≌△ABD(AAS),
∴BC=BD.
22.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°
∴∠CMA+∠ACM=90°,
∴∠ACM=∠DMB,
在Rt△ACM和Rt△BMD中,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴AC=BM=3m,
∴他到达点M时,运动时间为3÷1=3(s).
答:这个人从B点到M点运动了3s.
