江苏省南通市部分学校2023-2024学年九年级上学期12月月考数学试题(PDF版无答案)
文档属性
| 名称 | 江苏省南通市部分学校2023-2024学年九年级上学期12月月考数学试题(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 15:41:07 | ||
图片预览


文档简介
九年级数学试卷 20231213
注 意 事 项
考生在答题前请认真阅读本注意事项:
1.本试卷共 6 页,满分为 150 分,考试时间为 120 分钟。考试结束后,请将本试卷和答题卡一并交回。
2.答题前,请务必将自己的姓名、考试证号用 0.5 毫米黑色字迹的签字笔填写在试卷及答题卡上指定的位
置。
3.答案必须按要求填涂、书写在答题卡上,在试卷、草稿纸上答题一律无效。
一、选择题(本大题共 10 小题,每小题 3 分,共 30 分.在每小题给出的四个选项中,恰有一项是符合题
目要求的,请将正确选项的字母代号填涂在答.题.卡.相.应.位.置.上.)
1. 已知点 P 到圆心 O 的距离为 5,若点 P 在圆内,则⊙O 的半径可能为
A.3 B.4 C.5 D.6
2. 在△ABC 中,∠C=90°,AB=5,AC=4,下列三角函数表示正确的是
4 4 4 3
A.sinA B.cosA C.tanA D.tanB
5 5 3 4
k
3. 若点(2,3)在反比例函数 y= (k≠0)的图象上,那么下列各点在此图象上的是
x
A.(-2,3) B.(1,5) C.(1,6) D.(1,-6)
4. 如图,将∠CAB 放置在 5×5 的正方形网格中,则 tan∠CAB 的值是
5 10 1
A. B. C.2 D.
5 5 2
B
A A
C
A
C P
B
O
B α
A
B C C O
(第 4 题) (第 5 题) (第 6 题) (第 7 题) O
1
5. 如图,A,B,C 是⊙O 上的三个点,∠AOB= ∠BOC,∠BAC=45°,则∠ACB 的度数为
3
A.15° B.20° C.22.5° D.30°
6. 如图,若 P 为△ABC 的边 AB 上一点(AB>AC),则下列条件不一定能保证△ACP∽△ABC 的是
A.∠ACP=∠B B.∠APC=∠ACB
. AC AP . PC ACC D
AB AC BC AB
7. 如图,两个相邻的直角三角形,恰好能组合得到四边形 OABC.若 AB=BC=1,∠AOB=α,则 OC2
的值为
数学试卷 第 1 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
1
A. +1 B.sin2
1
α+1 C. +1 D.cos2α+1
sin 2 cos 2
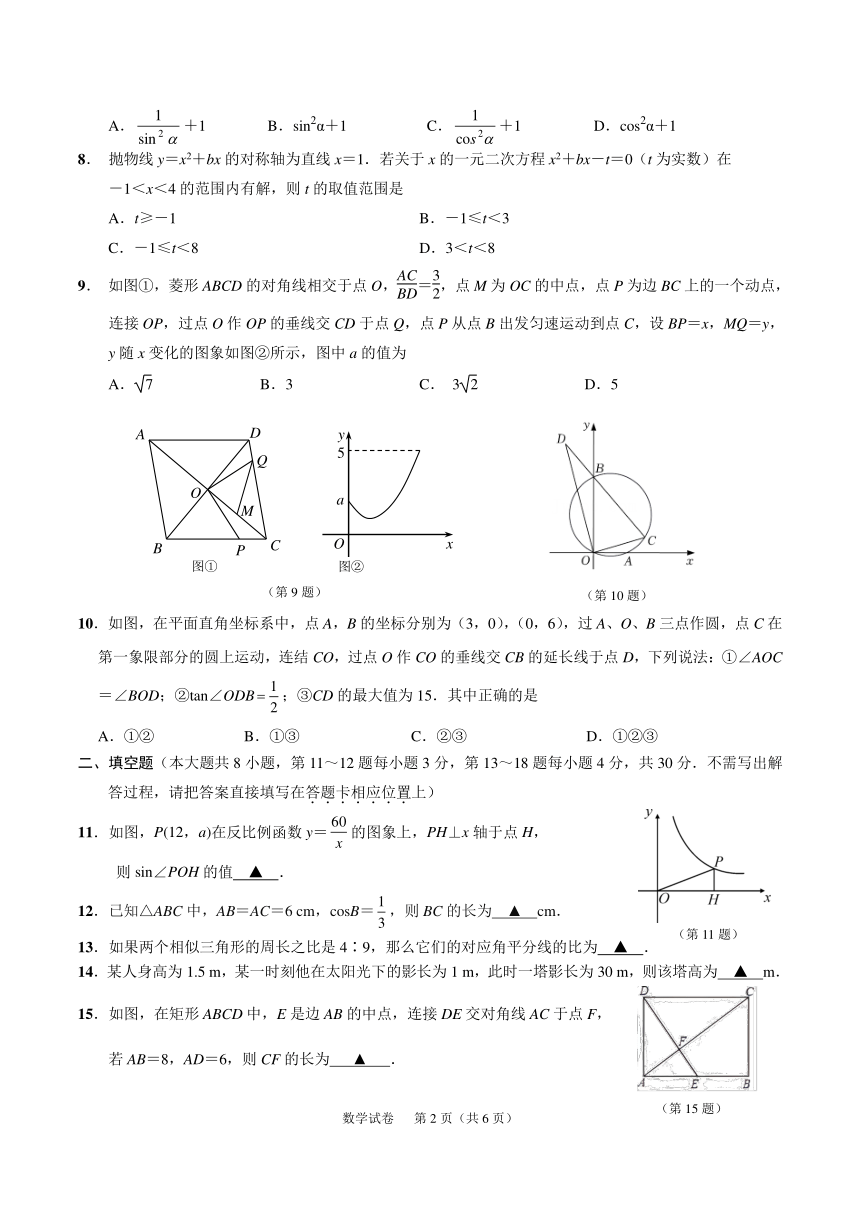
8. 抛物线 y=x2+bx 的对称轴为直线 x=1.若关于 x 的一元二次方程 x2+bx-t=0(t 为实数)在
-1<x<4 的范围内有解,则 t 的取值范围是
A.t≥-1 B.-1≤t<3
C.-1≤t<8 D.3<t<8
AC 3
9. 如图①,菱形 ABCD 的对角线相交于点 O, = ,点 M 为 OC 的中点,点 P 为边 BC 上的一个动点,
BD 2
连接 OP,过点 O 作 OP 的垂线交 CD 于点 Q,点 P 从点 B 出发匀速运动到点 C,设 BP=x,MQ=y,
y 随 x 变化的图象如图②所示,图中 a 的值为
A. 7 B.3 C. 3 2 D.5
A D y
5 Q
O a
M
B P C O x
图① 图②
(第 9 题) (第 10 题)
10.如图,在平面直角坐标系中,点 A,B 的坐标分别为(3,0),(0,6),过 A、O、B 三点作圆,点 C 在
第一象限部分的圆上运动,连结 CO,过点 O 作 CO 的垂线交 CB 的延长线于点 D,下列说法:①∠AOC
1
=∠BOD;②tan∠ODB ;③CD 的最大值为 15.其中正确的是
2
A.①② B.①③ C.②③ D.①②③
二、填空题(本大题共 8 小题,第 11~12 题每小题 3 分,第 13~18 题每小题 4 分,共 30 分.不需写出解
答过程,请把答案直接填写在答.题.卡.相.应.位.置.上)
60
11.如图,P(12,a)在反比例函数 y= 的图象上,PH⊥x 轴于点 H,
x
则 sin∠POH 的值 ▲ .
1
12.已知△ABC 中,AB=AC=6 cm,cosB= ,则 BC 的长为 ▲ cm.
3
(第 11 题)
13.如果两个相似三角形的周长之比是 4∶9,那么它们的对应角平分线的比为 ▲ .
14.某人身高为 1.5 m,某一时刻他在太阳光下的影长为 1 m,此时一塔影长为 30 m,则该塔高为 ▲ m.
15.如图,在矩形 ABCD 中,E 是边 AB 的中点,连接 DE 交对角线 AC 于点 F,
若 AB=8,AD=6,则 CF 的长为 ▲ .
(第 15 题)
数学试卷 第 2 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
16.如图,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点 O 到球心的长度为 50 cm,小球在左
右两个最高位置时,细绳相应所成的角为 74°,那么小球在最高和最低位置时的高度差为 ▲ cm.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
17.如图所示,在 Rt△OAB 中,∠OBA=90°,OA 在 x 轴上,AC 平分∠OAB,OD 平分∠AOB,AC 与 OD
k
相交于点 E,且 OC= 5.CE= 2,反比例函数 y= (k≠0,x>0)图象经过点 E,则 k 的值为 ▲ .
x
y
B
D
C
E
O
(第 17 题)
(第 16题)
18.定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等
弦圆”,现在有一个斜边长为 2 的等腰直角三角形,当等弦圆最大时,这个圆的半径为 ▲ .
三、解答题(本大题共 8 小题,共 90 分.请在答.题.卡.指.定.区.域.内作答,解答时应写出文字说明、证明过程
或演算步骤)
19.(本小题满分 10 分)
(1)计算:(1)sin245°+tan 60°cos 30°-tan 45°; (2) 2 (cos60 tan 30 )0 8 3(cos45 ) 1
20.(本小题满分 10 分)
在平面直角坐标系中,△ABC 的位置如图所示,每个小正方形的边长为 1,以原点 O 为位似中心,在
第一象限内,对△ABC 进行位似变换,得到△DEF(点 A,B,C 分别对应点 D,E,F),且△ABC 与△DEF
的相似比为 2:1.其中点 B 坐标为(4,2).
(1)画出△DEF;
(2)点 E 坐标为 ▲ ;
(3)线段 AC 上一点(x,y)经过变换后
对应的点的坐标为 ▲ .
(第 20 题)
数学试卷 第 3 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
21.(本小题满分 10 分)
如图,一扇窗户垂直打开,即 OM⊥OP,AC 是长度不变的滑动支架,其中一端固定在窗户的点 A 处,
另一端在 OP 上滑动,将窗户 OM 按图示方向向内旋转 45°到达 ON 位置,此时,点 A、C 的对应位置
分别是点 B、D.测量出∠ODB 为 30°,点 D 到点 O 的距离为 40 cm.
(1)求 B 点到 OP 的距离;(2)求滑动支架的长.(结果保留根号).
(第 21 题)
22.(本小题满分 10 分)
如图,AB 与⊙O 相切于点 A,半径 OC∥AB,BC 与⊙O 相交于点 D,连接 AD.
(1)求证:∠OCA=∠ADC;
1
(2)若 AD=2,tanB= ,求 OC 的长.
3
C O
D
A
B
(第 22 题)
23.(本小题满分 12 分)
1 k
如图,在平面直角坐标系中,一次函数 y x b与反比例函数 y 交于第一象限内 A,B(6,1)
2 x
两点(B 在 A 右侧),分别交 x 轴,y 轴于 C,D 两点.
(1)求 k 和 b 的值;
(2)求点 A 的坐标;
(3)在 y 轴上是否存在一点 P,使以 A,D,P 为顶点的三角形与△CDO 相似?若存在,求出点 P 的
坐标.若不存在,请说明理由.
.
(第 23 题)
数学试卷 第 4 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
24.(本小题满分 10 分)
如图,△ABC 中,∠ACB=90°,AC=4 厘米,BC=6 厘米,D 是 BC 的中点.点 E 从 A 出发,以 a 厘
米/秒(a>0)的速度沿 AC 匀速向点 C 运动,点 F 同时以 1 厘米/秒的速度从 C 出发,沿 CB匀速向点
B 运动,其中一个动点到达端点时,另一个动点也随之停止运动,过点 E 作 AC 的垂线,交 AD 于点 G,
连接 EF,FG.设它们运动的时间为 t 秒(t>0).
(1)当 t=2 时,△ECF∽△BCA,求 a 的值;
1
(2)当 a= 时,以点 E、F、D、G 为顶点的四边形是平行四边形,求 t 的值;
2
(第 24 题)
25.(本小题满分 14 分)
已知:矩形 ABCD 中,AB=6,BC=8,点 E,F 分别在边 AD,边 AB 的延长线上,且 4DE=3BF.
CE
(1)如图 1,连接 CF,CE,求 的值;
EF
3
(2)如图 2,点 M,N 分别在 AB,AD 上,MN 与 EF 交于点 G,且 tan∠EGN= ,若 MN=4 5,
4
求 BF 的长;
(3)如图 3,BD 与 EF 交于点 K,连接 CK,若 DE=3,求 CK 的长.
D D N C
D C
C
E
E E
G
K
A B F A M F
B A B F
图 1 图 2 图 3
(第 25 题)
数学试卷 第 5 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
26.(本小题满分 14 分)
1
抛物线 y= x2+bx+c 经过点 A(0,-4)且与 x 轴相交于点 B(-1, 0)和 C,O 为坐标原点.
2
(1)求抛物线的解析式;
1
(2)将抛物线 y= x2+bx+c 向上平移 7 个单位长度,再向左平移 m(m>0)个单位长度,得到新抛
2
物线,若新抛物线的顶点 P 在△ABC 内,求 m 的取值范围;
(3)将 x 轴下方的抛物线图象关于 x 轴对称,得到新的函数图象 C,若直线 y=x+k 与图象 C 始终有
3 个交点,求满足条件的 k 的值.
数学试卷 第 6 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
注 意 事 项
考生在答题前请认真阅读本注意事项:
1.本试卷共 6 页,满分为 150 分,考试时间为 120 分钟。考试结束后,请将本试卷和答题卡一并交回。
2.答题前,请务必将自己的姓名、考试证号用 0.5 毫米黑色字迹的签字笔填写在试卷及答题卡上指定的位
置。
3.答案必须按要求填涂、书写在答题卡上,在试卷、草稿纸上答题一律无效。
一、选择题(本大题共 10 小题,每小题 3 分,共 30 分.在每小题给出的四个选项中,恰有一项是符合题
目要求的,请将正确选项的字母代号填涂在答.题.卡.相.应.位.置.上.)
1. 已知点 P 到圆心 O 的距离为 5,若点 P 在圆内,则⊙O 的半径可能为
A.3 B.4 C.5 D.6
2. 在△ABC 中,∠C=90°,AB=5,AC=4,下列三角函数表示正确的是
4 4 4 3
A.sinA B.cosA C.tanA D.tanB
5 5 3 4
k
3. 若点(2,3)在反比例函数 y= (k≠0)的图象上,那么下列各点在此图象上的是
x
A.(-2,3) B.(1,5) C.(1,6) D.(1,-6)
4. 如图,将∠CAB 放置在 5×5 的正方形网格中,则 tan∠CAB 的值是
5 10 1
A. B. C.2 D.
5 5 2
B
A A
C
A
C P
B
O
B α
A
B C C O
(第 4 题) (第 5 题) (第 6 题) (第 7 题) O
1
5. 如图,A,B,C 是⊙O 上的三个点,∠AOB= ∠BOC,∠BAC=45°,则∠ACB 的度数为
3
A.15° B.20° C.22.5° D.30°
6. 如图,若 P 为△ABC 的边 AB 上一点(AB>AC),则下列条件不一定能保证△ACP∽△ABC 的是
A.∠ACP=∠B B.∠APC=∠ACB
. AC AP . PC ACC D
AB AC BC AB
7. 如图,两个相邻的直角三角形,恰好能组合得到四边形 OABC.若 AB=BC=1,∠AOB=α,则 OC2
的值为
数学试卷 第 1 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
1
A. +1 B.sin2
1
α+1 C. +1 D.cos2α+1
sin 2 cos 2
8. 抛物线 y=x2+bx 的对称轴为直线 x=1.若关于 x 的一元二次方程 x2+bx-t=0(t 为实数)在
-1<x<4 的范围内有解,则 t 的取值范围是
A.t≥-1 B.-1≤t<3
C.-1≤t<8 D.3<t<8
AC 3
9. 如图①,菱形 ABCD 的对角线相交于点 O, = ,点 M 为 OC 的中点,点 P 为边 BC 上的一个动点,
BD 2
连接 OP,过点 O 作 OP 的垂线交 CD 于点 Q,点 P 从点 B 出发匀速运动到点 C,设 BP=x,MQ=y,
y 随 x 变化的图象如图②所示,图中 a 的值为
A. 7 B.3 C. 3 2 D.5
A D y
5 Q
O a
M
B P C O x
图① 图②
(第 9 题) (第 10 题)
10.如图,在平面直角坐标系中,点 A,B 的坐标分别为(3,0),(0,6),过 A、O、B 三点作圆,点 C 在
第一象限部分的圆上运动,连结 CO,过点 O 作 CO 的垂线交 CB 的延长线于点 D,下列说法:①∠AOC
1
=∠BOD;②tan∠ODB ;③CD 的最大值为 15.其中正确的是
2
A.①② B.①③ C.②③ D.①②③
二、填空题(本大题共 8 小题,第 11~12 题每小题 3 分,第 13~18 题每小题 4 分,共 30 分.不需写出解
答过程,请把答案直接填写在答.题.卡.相.应.位.置.上)
60
11.如图,P(12,a)在反比例函数 y= 的图象上,PH⊥x 轴于点 H,
x
则 sin∠POH 的值 ▲ .
1
12.已知△ABC 中,AB=AC=6 cm,cosB= ,则 BC 的长为 ▲ cm.
3
(第 11 题)
13.如果两个相似三角形的周长之比是 4∶9,那么它们的对应角平分线的比为 ▲ .
14.某人身高为 1.5 m,某一时刻他在太阳光下的影长为 1 m,此时一塔影长为 30 m,则该塔高为 ▲ m.
15.如图,在矩形 ABCD 中,E 是边 AB 的中点,连接 DE 交对角线 AC 于点 F,
若 AB=8,AD=6,则 CF 的长为 ▲ .
(第 15 题)
数学试卷 第 2 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
16.如图,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点 O 到球心的长度为 50 cm,小球在左
右两个最高位置时,细绳相应所成的角为 74°,那么小球在最高和最低位置时的高度差为 ▲ cm.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
17.如图所示,在 Rt△OAB 中,∠OBA=90°,OA 在 x 轴上,AC 平分∠OAB,OD 平分∠AOB,AC 与 OD
k
相交于点 E,且 OC= 5.CE= 2,反比例函数 y= (k≠0,x>0)图象经过点 E,则 k 的值为 ▲ .
x
y
B
D
C
E
O
(第 17 题)
(第 16题)
18.定义:有一个圆分别和一个三角形的三条边各有两个交点,截得的三条弦相等,我们把这个圆叫作“等
弦圆”,现在有一个斜边长为 2 的等腰直角三角形,当等弦圆最大时,这个圆的半径为 ▲ .
三、解答题(本大题共 8 小题,共 90 分.请在答.题.卡.指.定.区.域.内作答,解答时应写出文字说明、证明过程
或演算步骤)
19.(本小题满分 10 分)
(1)计算:(1)sin245°+tan 60°cos 30°-tan 45°; (2) 2 (cos60 tan 30 )0 8 3(cos45 ) 1
20.(本小题满分 10 分)
在平面直角坐标系中,△ABC 的位置如图所示,每个小正方形的边长为 1,以原点 O 为位似中心,在
第一象限内,对△ABC 进行位似变换,得到△DEF(点 A,B,C 分别对应点 D,E,F),且△ABC 与△DEF
的相似比为 2:1.其中点 B 坐标为(4,2).
(1)画出△DEF;
(2)点 E 坐标为 ▲ ;
(3)线段 AC 上一点(x,y)经过变换后
对应的点的坐标为 ▲ .
(第 20 题)
数学试卷 第 3 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
21.(本小题满分 10 分)
如图,一扇窗户垂直打开,即 OM⊥OP,AC 是长度不变的滑动支架,其中一端固定在窗户的点 A 处,
另一端在 OP 上滑动,将窗户 OM 按图示方向向内旋转 45°到达 ON 位置,此时,点 A、C 的对应位置
分别是点 B、D.测量出∠ODB 为 30°,点 D 到点 O 的距离为 40 cm.
(1)求 B 点到 OP 的距离;(2)求滑动支架的长.(结果保留根号).
(第 21 题)
22.(本小题满分 10 分)
如图,AB 与⊙O 相切于点 A,半径 OC∥AB,BC 与⊙O 相交于点 D,连接 AD.
(1)求证:∠OCA=∠ADC;
1
(2)若 AD=2,tanB= ,求 OC 的长.
3
C O
D
A
B
(第 22 题)
23.(本小题满分 12 分)
1 k
如图,在平面直角坐标系中,一次函数 y x b与反比例函数 y 交于第一象限内 A,B(6,1)
2 x
两点(B 在 A 右侧),分别交 x 轴,y 轴于 C,D 两点.
(1)求 k 和 b 的值;
(2)求点 A 的坐标;
(3)在 y 轴上是否存在一点 P,使以 A,D,P 为顶点的三角形与△CDO 相似?若存在,求出点 P 的
坐标.若不存在,请说明理由.
.
(第 23 题)
数学试卷 第 4 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
24.(本小题满分 10 分)
如图,△ABC 中,∠ACB=90°,AC=4 厘米,BC=6 厘米,D 是 BC 的中点.点 E 从 A 出发,以 a 厘
米/秒(a>0)的速度沿 AC 匀速向点 C 运动,点 F 同时以 1 厘米/秒的速度从 C 出发,沿 CB匀速向点
B 运动,其中一个动点到达端点时,另一个动点也随之停止运动,过点 E 作 AC 的垂线,交 AD 于点 G,
连接 EF,FG.设它们运动的时间为 t 秒(t>0).
(1)当 t=2 时,△ECF∽△BCA,求 a 的值;
1
(2)当 a= 时,以点 E、F、D、G 为顶点的四边形是平行四边形,求 t 的值;
2
(第 24 题)
25.(本小题满分 14 分)
已知:矩形 ABCD 中,AB=6,BC=8,点 E,F 分别在边 AD,边 AB 的延长线上,且 4DE=3BF.
CE
(1)如图 1,连接 CF,CE,求 的值;
EF
3
(2)如图 2,点 M,N 分别在 AB,AD 上,MN 与 EF 交于点 G,且 tan∠EGN= ,若 MN=4 5,
4
求 BF 的长;
(3)如图 3,BD 与 EF 交于点 K,连接 CK,若 DE=3,求 CK 的长.
D D N C
D C
C
E
E E
G
K
A B F A M F
B A B F
图 1 图 2 图 3
(第 25 题)
数学试卷 第 5 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
26.(本小题满分 14 分)
1
抛物线 y= x2+bx+c 经过点 A(0,-4)且与 x 轴相交于点 B(-1, 0)和 C,O 为坐标原点.
2
(1)求抛物线的解析式;
1
(2)将抛物线 y= x2+bx+c 向上平移 7 个单位长度,再向左平移 m(m>0)个单位长度,得到新抛
2
物线,若新抛物线的顶点 P 在△ABC 内,求 m 的取值范围;
(3)将 x 轴下方的抛物线图象关于 x 轴对称,得到新的函数图象 C,若直线 y=x+k 与图象 C 始终有
3 个交点,求满足条件的 k 的值.
数学试卷 第 6 页(共 6 页)
{#{QQABaYwQggCIABIAABhCEQWqCAKQkAEACAoORAAEMAABQBFABAA=}#}
同课章节目录
