正方形教案
图片预览

文档简介
公开课《正方形》教案
课 题: 2 1.3 正方形
授课教师: 王 南 林
授课班级:安庆市外国语学校初二(5)班
授课时间:2007.05.25.
一、教学目标
知识与技能
1、理解正方形的概念,了解正方形与平行四边形、菱形、矩形的关系.
2、掌握正方形的有关性质和判定方法.
3、能运用正方形的性质解决有关计算和证明问题.
过程与方法
1、通过观察、实验、归纳、类比获得数学猜想,发展学生的合情推理能力,进一步提高学生逻辑思维能力.
2、通过四边形从属关系的教学,渗透集合思想.
情感态度与价值观
1、经历探索正方形有关性质和四边形成为正方形的条件过程,培养学生动手操作的能力、主动探究的习惯和合作交流的意识.
2、通过理解特殊的平行四边形之间的内在联系,培养学生辩证观点.
二、教学重难点
教学重点:正方形的定义和性质
教学难点:四边形成为正方形的条件
教学关键:正方形与平行四边形、菱形、矩形的关系
三、教学方法
教学方法:探究法
教学手段:多媒体辅助教学 几何模型
四、教学流程
(一)创设情境,导入新知
Ⅰ、导言 我们已学习了矩形、菱形,它们都是特殊的平行四边形.
Ⅱ、抢答 1、让学生根据所准备的模型分别叙述矩形、菱形的定义及其性质.
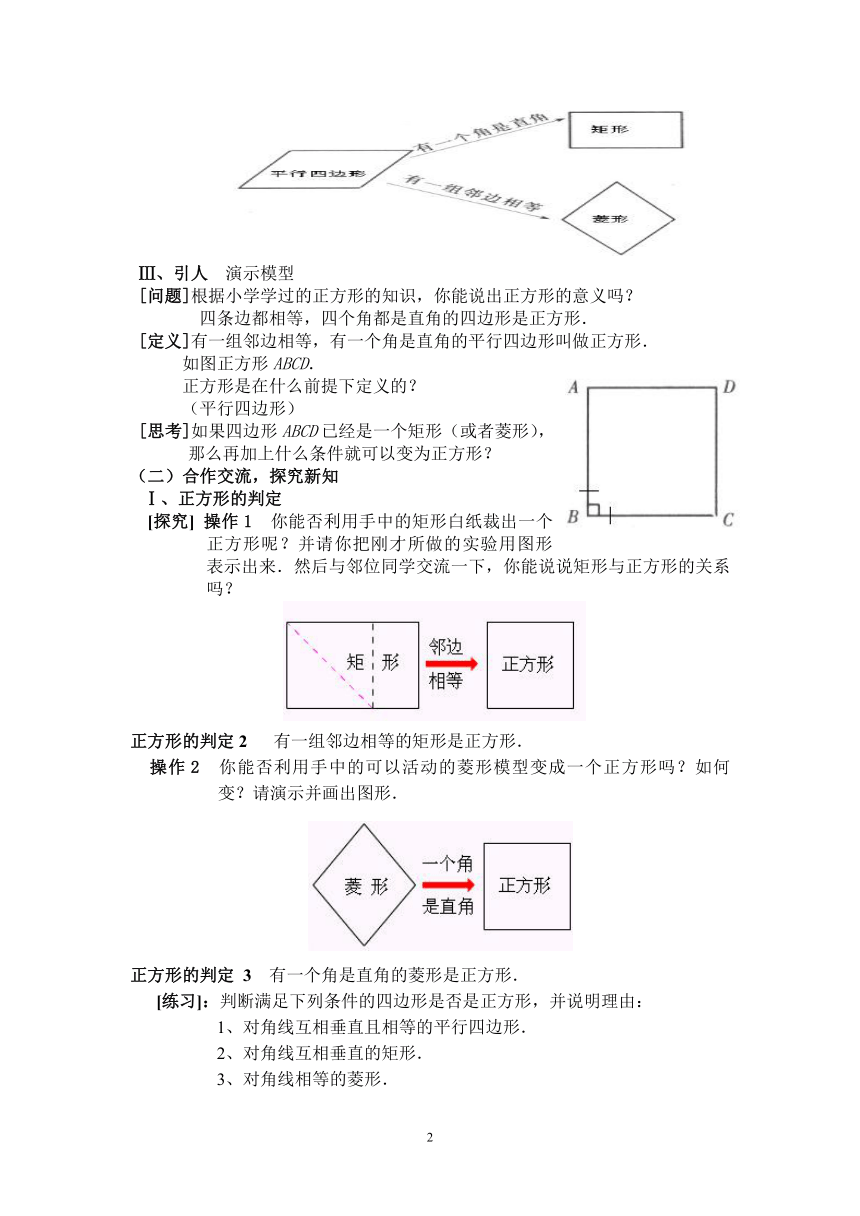
2、平行四边形,矩形,菱形的内在联系.
Ⅲ、引人 演示模型
[问题]根据小学学过的正方形的知识,你能说出正方形的意义吗?
四条边都相等,四个角都是直角的四边形是正方形.
[定义]有一组邻边相等,有一个角是直角的平行四边形叫做正方形.
如图正方形ABCD.
正方形是在什么前提下定义的?
(平行四边形)
[思考]如果四边形ABCD已经是一个矩形(或者菱形), 那么再加上什么条件就可以变为正方形?
(二)合作交流,探究新知
Ⅰ、正方形的判定
[探究] 操作1 你能否利用手中的矩形白纸裁出一个正方形呢?并请你把刚才所做的实验用图形表示出来.然后与邻位同学交流一下,你能说说矩形与正方形的关系吗?
正方形的判定2 有一组邻边相等的矩形是正方形.
操作2 你能否利用手中的可以活动的菱形模型变成一个正方形吗?如何变?请演示并画出图形.
正方形的判定 3 有一个角是直角的菱形是正方形.
[练习]:判断满足下列条件的四边形是否是正方形,并说明理由:
1、对角线互相垂直且相等的平行四边形.
2、对角线互相垂直的矩形.
3、对角线相等的菱形.
4、对角线互相垂直平分且相等的四边形.
[归纳]正方形与矩形、菱形、平行四边形间的关系如图.
Ⅱ、正方形的性质
[交流]根据上述关系可知,正方形既是特殊的矩 形、又是特殊的菱形,更是的特殊的平行四边形,你能说出正方形的性质吗?
[点拨]从边、角、对角线等方面考虑.
边:对边平行、四条边都相等
角:四个角都是直角
对角线:对角线相等,互相垂直平分,每条对角线平分一组对角
[归纳]性质1:正方形的四条边都相等,四个角都是直角.
性质2:正方形的两条对角线相等且互相垂直平分,每条对角线平分一组对角.
[问题]正方形是中心对称图形吗?如是,对称中心在哪里?
正方形是轴对称图形吗?如是,它有几条对称轴?
对称性:正方形是中心对称图形;同时还是轴对称图形,它有四条对称轴(两条对角线,两组对边的中垂线.),对称轴通过对称中心.如图
正方形具有平行四边形、矩形、菱形的一切性质.
(三)应用迁移,巩固提高
Ⅰ、[问题] 如图,四边形ABCD是正方形,两条对角线相交于点O.
(1)一条对角线把它分成_______个全等的________ 三角形;
(2)两条对角线把它分成_______个全等的________三角形;
图中一共有________个等腰直角三角形;
(3)∠AOB=_____度,∠OAB=_____度.
(4)AB: AO: AC=________.
Ⅱ、例6、如图,点A'、B'、C'、D'分别是正方形ABCD 四条边上的点,并且AA'=BB'=CC'=DD'.
求证:四边形A'B'C'D'是正方形.
证明: 因为四边形ABCD是正方形,所以
AB=BC=CD=DA.
又 ∵AA'=BB'=CC'=DD',
∴D'A=A'B=B'C=C'D.
∵∠A=∠B=∠C=∠D=900,
∴△AA'D'≌△BB'A'
≌△CC'B'≌△DD'C',(SAS)
∴A'B'=B'C'=C'D'=D'A',
即四边形A'B'C'D'是菱形.
又 ∵∠1=∠3,∠1+∠2=900,
∴∠2+∠3=900,∴∠D'A'B'=900.
所以四边形A'B'C'D'是正方形.
Ⅲ、[论证]课本第77页练习3:
如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形.求证:△ABF≌△DAE.
证明:∵四边形EFGH是正方形,
∴∠AFB=∠DEA=900, 且 ∠ABF+∠BAF=900,
又∵∠BAF+∠DAE=900, ∴∠ABF=∠DAE.
又∵AB=DA, ∴△ABF≌△DAE(AAS).
(四)整理反思、评价体验
通过这节课的学习,我们有哪些收获?
引导学生从知识内容、数学思想方法两方面进行小结.
正方形的定义、判定方法和性质.
1、正方形与 矩形,菱形,平行四边形的关系.
2、正方形的性质:
正方形具有矩形和菱形的一切性质
a 边: 四条边都相等
(性质1)
b 角: 四个角都是直角
c 对角线:相等.互相垂直平分,
每条对角线平分一组对角 (性质2)
正方形的性质与平行四边形、矩形、菱形的性质可比较如下:
(师生同完成,凡是图形所具有的性质,在表中相应的空格中填上“√”,没有的性质不要填写)
由表中可知:因为正方形既是特殊的平行四边形,又是特殊的矩形,特殊的菱形,所以正方形具有平行四边形、矩形、菱形的一切性质,又具有自身的特殊性质.
(五)课后作业
Ⅰ、课本P78习题21.3 3(2)、 12
P89习题A组复习题 11
Ⅱ、课本P77“阅读与思考----完美矩形与完美正方形”
PAGE
1
课 题: 2 1.3 正方形
授课教师: 王 南 林
授课班级:安庆市外国语学校初二(5)班
授课时间:2007.05.25.
一、教学目标
知识与技能
1、理解正方形的概念,了解正方形与平行四边形、菱形、矩形的关系.
2、掌握正方形的有关性质和判定方法.
3、能运用正方形的性质解决有关计算和证明问题.
过程与方法
1、通过观察、实验、归纳、类比获得数学猜想,发展学生的合情推理能力,进一步提高学生逻辑思维能力.
2、通过四边形从属关系的教学,渗透集合思想.
情感态度与价值观
1、经历探索正方形有关性质和四边形成为正方形的条件过程,培养学生动手操作的能力、主动探究的习惯和合作交流的意识.
2、通过理解特殊的平行四边形之间的内在联系,培养学生辩证观点.
二、教学重难点
教学重点:正方形的定义和性质
教学难点:四边形成为正方形的条件
教学关键:正方形与平行四边形、菱形、矩形的关系
三、教学方法
教学方法:探究法
教学手段:多媒体辅助教学 几何模型
四、教学流程
(一)创设情境,导入新知
Ⅰ、导言 我们已学习了矩形、菱形,它们都是特殊的平行四边形.
Ⅱ、抢答 1、让学生根据所准备的模型分别叙述矩形、菱形的定义及其性质.
2、平行四边形,矩形,菱形的内在联系.
Ⅲ、引人 演示模型
[问题]根据小学学过的正方形的知识,你能说出正方形的意义吗?
四条边都相等,四个角都是直角的四边形是正方形.
[定义]有一组邻边相等,有一个角是直角的平行四边形叫做正方形.
如图正方形ABCD.
正方形是在什么前提下定义的?
(平行四边形)
[思考]如果四边形ABCD已经是一个矩形(或者菱形), 那么再加上什么条件就可以变为正方形?
(二)合作交流,探究新知
Ⅰ、正方形的判定
[探究] 操作1 你能否利用手中的矩形白纸裁出一个正方形呢?并请你把刚才所做的实验用图形表示出来.然后与邻位同学交流一下,你能说说矩形与正方形的关系吗?
正方形的判定2 有一组邻边相等的矩形是正方形.
操作2 你能否利用手中的可以活动的菱形模型变成一个正方形吗?如何变?请演示并画出图形.
正方形的判定 3 有一个角是直角的菱形是正方形.
[练习]:判断满足下列条件的四边形是否是正方形,并说明理由:
1、对角线互相垂直且相等的平行四边形.
2、对角线互相垂直的矩形.
3、对角线相等的菱形.
4、对角线互相垂直平分且相等的四边形.
[归纳]正方形与矩形、菱形、平行四边形间的关系如图.
Ⅱ、正方形的性质
[交流]根据上述关系可知,正方形既是特殊的矩 形、又是特殊的菱形,更是的特殊的平行四边形,你能说出正方形的性质吗?
[点拨]从边、角、对角线等方面考虑.
边:对边平行、四条边都相等
角:四个角都是直角
对角线:对角线相等,互相垂直平分,每条对角线平分一组对角
[归纳]性质1:正方形的四条边都相等,四个角都是直角.
性质2:正方形的两条对角线相等且互相垂直平分,每条对角线平分一组对角.
[问题]正方形是中心对称图形吗?如是,对称中心在哪里?
正方形是轴对称图形吗?如是,它有几条对称轴?
对称性:正方形是中心对称图形;同时还是轴对称图形,它有四条对称轴(两条对角线,两组对边的中垂线.),对称轴通过对称中心.如图
正方形具有平行四边形、矩形、菱形的一切性质.
(三)应用迁移,巩固提高
Ⅰ、[问题] 如图,四边形ABCD是正方形,两条对角线相交于点O.
(1)一条对角线把它分成_______个全等的________ 三角形;
(2)两条对角线把它分成_______个全等的________三角形;
图中一共有________个等腰直角三角形;
(3)∠AOB=_____度,∠OAB=_____度.
(4)AB: AO: AC=________.
Ⅱ、例6、如图,点A'、B'、C'、D'分别是正方形ABCD 四条边上的点,并且AA'=BB'=CC'=DD'.
求证:四边形A'B'C'D'是正方形.
证明: 因为四边形ABCD是正方形,所以
AB=BC=CD=DA.
又 ∵AA'=BB'=CC'=DD',
∴D'A=A'B=B'C=C'D.
∵∠A=∠B=∠C=∠D=900,
∴△AA'D'≌△BB'A'
≌△CC'B'≌△DD'C',(SAS)
∴A'B'=B'C'=C'D'=D'A',
即四边形A'B'C'D'是菱形.
又 ∵∠1=∠3,∠1+∠2=900,
∴∠2+∠3=900,∴∠D'A'B'=900.
所以四边形A'B'C'D'是正方形.
Ⅲ、[论证]课本第77页练习3:
如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形.求证:△ABF≌△DAE.
证明:∵四边形EFGH是正方形,
∴∠AFB=∠DEA=900, 且 ∠ABF+∠BAF=900,
又∵∠BAF+∠DAE=900, ∴∠ABF=∠DAE.
又∵AB=DA, ∴△ABF≌△DAE(AAS).
(四)整理反思、评价体验
通过这节课的学习,我们有哪些收获?
引导学生从知识内容、数学思想方法两方面进行小结.
正方形的定义、判定方法和性质.
1、正方形与 矩形,菱形,平行四边形的关系.
2、正方形的性质:
正方形具有矩形和菱形的一切性质
a 边: 四条边都相等
(性质1)
b 角: 四个角都是直角
c 对角线:相等.互相垂直平分,
每条对角线平分一组对角 (性质2)
正方形的性质与平行四边形、矩形、菱形的性质可比较如下:
(师生同完成,凡是图形所具有的性质,在表中相应的空格中填上“√”,没有的性质不要填写)
由表中可知:因为正方形既是特殊的平行四边形,又是特殊的矩形,特殊的菱形,所以正方形具有平行四边形、矩形、菱形的一切性质,又具有自身的特殊性质.
(五)课后作业
Ⅰ、课本P78习题21.3 3(2)、 12
P89习题A组复习题 11
Ⅱ、课本P77“阅读与思考----完美矩形与完美正方形”
PAGE
1
