2.2.1直线与平面平行的判定
文档属性
| 名称 | 2.2.1直线与平面平行的判定 |

|
|
| 格式 | rar | ||
| 文件大小 | 241.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-29 00:00:00 | ||
图片预览


文档简介
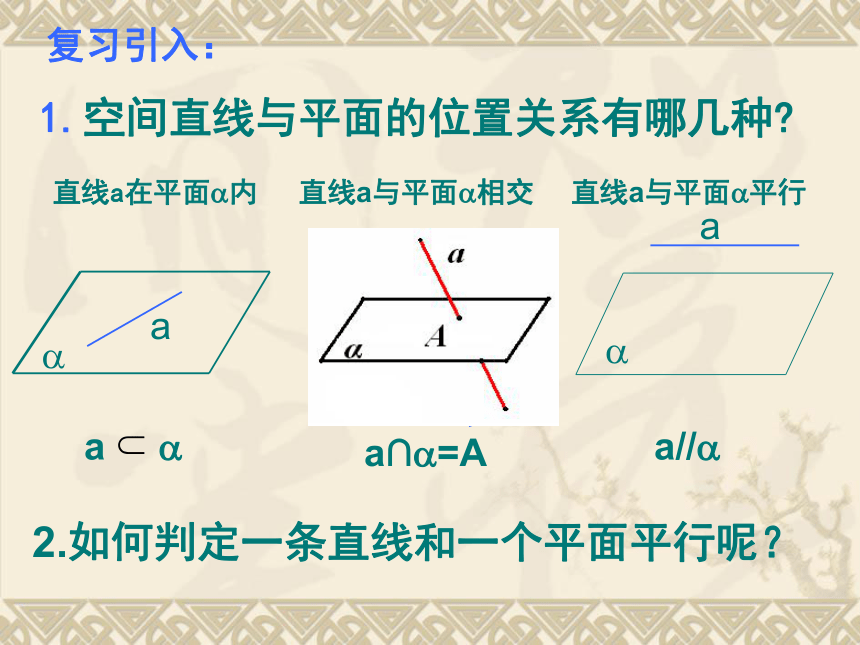
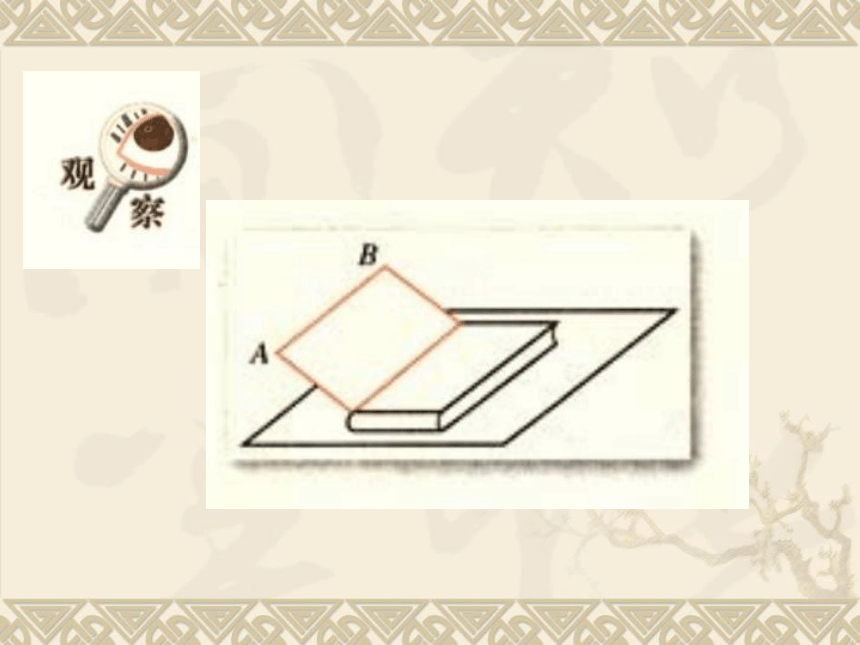
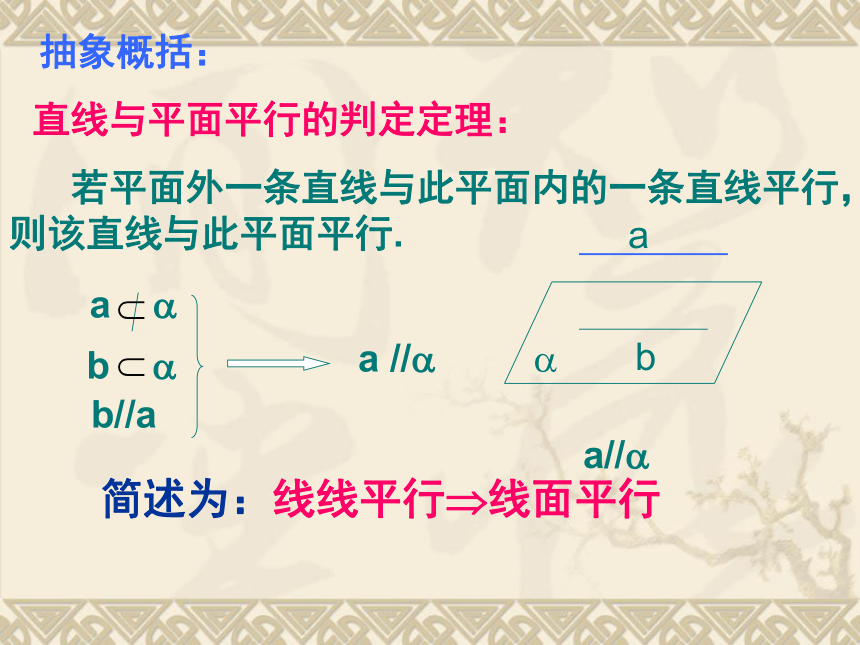
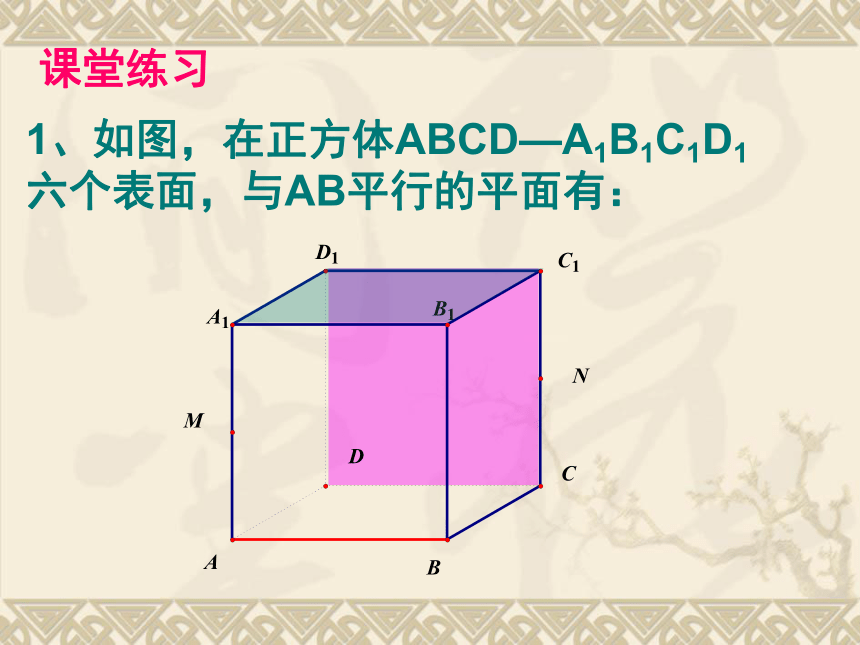
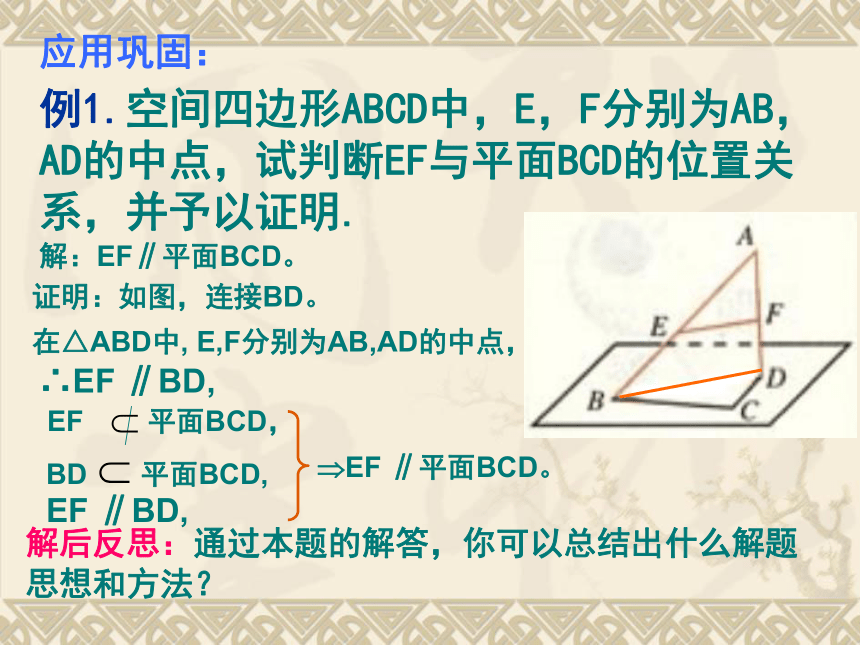
课件14张PPT。2.2.1直线与平面平行的判定1.空间直线与平面的位置关系有哪几种?复习引入:2.如何判定一条直线和一个平面平行呢?实例探究:抽象概括:直线与平面平行的判定定理: 若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.简述为:线线平行?线面平行课堂练习1、如图,在正方体ABCD—A1B1C1D1 六个表面,与AB平行的平面有: 应用巩固:例1.空间四边形ABCD中,E,F分别为AB,AD的中点,试判断EF与平面BCD的位置关系,并予以证明.解:EF∥平面BCD。证明:如图,连接BD。∴EF ∥BD,?EF ∥平面BCD。解后反思:通过本题的解答,你可以总结出什么解题思想和方法?在△ABD中, E,F分别为AB,AD的中点,EF ∥BD,反思1:要证明直线与平面平行可以运用判定定理;反思2:能够运用定理的条件是要满足六个字,
“面外、面内、平行”。反思3:运用定理的关键是找平行线。找平行线经常用三角形中位线定理。例2、如图,在正方体ABCD-A1B1C1D1中,E、F分别是棱BC与C1D1的中点。
求证:EF//平面BDD1B1.例2、如图,在正方体ABCD-A1B1C1D1中,E、F分别是棱BC与C1D1的中点。求证:EF//平面BDD1B1.P56 练习2FE练习3: 3.如图,四棱锥A—DBCE中,
O为底面正方形DBCE对角线
的交点,F为AE的中点.
求证:AB//平面DCF. 分析:要证明AB//平面DCF,只需要在平面DCF中找一条
直线与AB平行即可。2.应用判定定理判定线面平行时应注意六个字:
(1)面外,(2)面内,(3)平行。小结:1.直线与平面平行的判定:3.应用判定定理判定线面平行的关键是找平行线方法一:三角形的中位线定理;方法二:平行四边形的平行关系。作业:
A:P61 1、2做书上
B:P62 3、4做作业本上
“面外、面内、平行”。反思3:运用定理的关键是找平行线。找平行线经常用三角形中位线定理。例2、如图,在正方体ABCD-A1B1C1D1中,E、F分别是棱BC与C1D1的中点。
求证:EF//平面BDD1B1.例2、如图,在正方体ABCD-A1B1C1D1中,E、F分别是棱BC与C1D1的中点。求证:EF//平面BDD1B1.P56 练习2FE练习3: 3.如图,四棱锥A—DBCE中,
O为底面正方形DBCE对角线
的交点,F为AE的中点.
求证:AB//平面DCF. 分析:要证明AB//平面DCF,只需要在平面DCF中找一条
直线与AB平行即可。2.应用判定定理判定线面平行时应注意六个字:
(1)面外,(2)面内,(3)平行。小结:1.直线与平面平行的判定:3.应用判定定理判定线面平行的关键是找平行线方法一:三角形的中位线定理;方法二:平行四边形的平行关系。作业:
A:P61 1、2做书上
B:P62 3、4做作业本上
