选修三 基本计数原理
图片预览











文档简介
课件30张PPT。基本计数原理青州二中 王明华
课堂引入 张、黄、李、赵四位好朋友约定在寒假中要互寄贺年片一张,他们一共寄了多少张贺年片?
如果他们约定在寒假中每两人通话一次,以祝贺新年,那么,他们的通话次数一共有多少呢?
问题 1. 从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有4 班, 汽车有2班,轮船有3班。那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法?
分析: 从甲地到乙地有3类办法,
第一类办法, 乘火车,有4种方法;
第二类办法, 乘汽车,有2种方法;
第三类办法, 乘轮船, 有3种方法;
所以 从甲地到乙地共有 4 + 2 + 3 = 9 种方法。
分类加法计数原理 做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法。那么完成这件事共有
N=m1+m2+…+mn
种不同的方法。
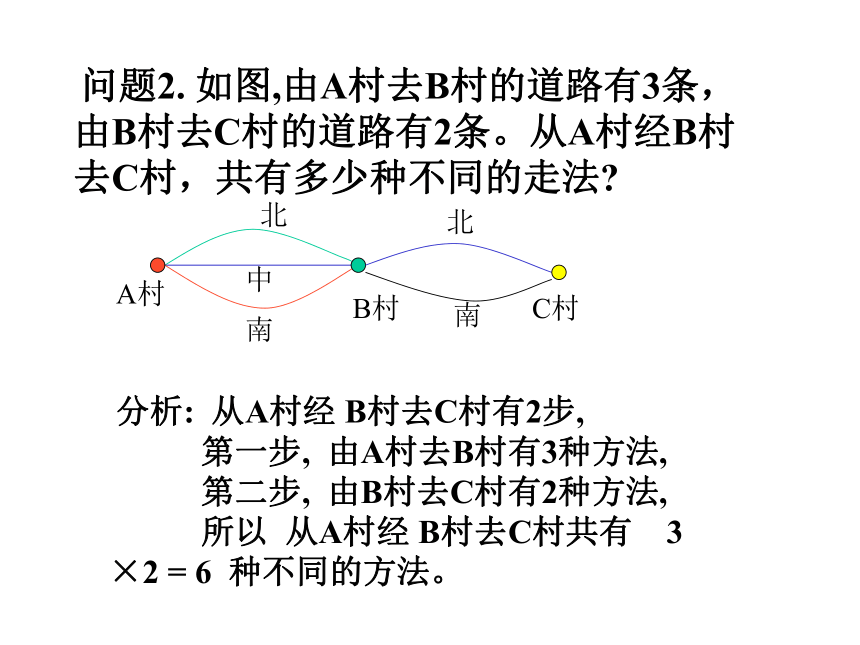
问题2. 如图,由A村去B村的道路有3条,由B村去C村的道路有2条。从A村经B村去C村,共有多少种不同的走法?
A村B村C村北南中北南 分析: 从A村经 B村去C村有2步,
第一步, 由A村去B村有3种方法,
第二步, 由B村去C村有2种方法,
所以 从A村经 B村去C村共有 3 ×2 = 6 种不同的方法。
分步乘法计数原理 做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
N=m1×m2×…×mn
种不同的方法。
思考: 分类加法计数原理与分步乘法计数原理有何共同之处?它们的区别在哪里?1 两个原理都用来研究解决完成一件事情,共有多少种不同方法的问题。
2 区别在于:它们研究完成一件事情的方式不同。分类计数原理是“分类”完成,即各类方法中的任何一种都可以把这件事做完;而分步计数原理是“分步”完成,即每一个步骤中的任何一种方法都不能把这件事情做完,各个步骤顺次相依,只有把各个步骤依次完成,才能把这件事情做完。
例题
例 1 一个三层书架的上层放有5本不同的数学书,中间放有3本不同的语文书,下层放有2本不同的英语书。
(1)从书架上任取一本书,有多少种不同的取法?
(2)从书架上任取三本书,其中数学书、语文书、英语书各一本,有多少种不同的取法?
解:(1)从书架上任取一本书,有三类办法:
第一类办法 从书架上层任取一本数学书,有5种不同的方法;
第二类办法 从书架中层任取一本语文书,有3种不同的方法;
第三类办法 从书架下层任取一本英语书,有2种不同的方法.
只要从书架上任意取出一本书,任务即完成,由分类加法计数原理,不同的取法共有
N=5+3+2=10(种)
解:
(2)从书架上任取三本书,其中数学书、语文书、英语书各一本,可以分三个步骤完成:
第一步 从书架上任取一本数学书,有5种不同的方法;
第二步 从书架上任取一本语文书,有3种不同的方法;
第三步 从书架上任取一本英语书,有2种不同的方法;
由分步乘法计数原理,不同的取法共有
N=5×3×2=30(种)
所以从书架上任取三本书,其中数学书、语文书、英语书各一本,共有30种不同的取法。
总结: 解题的关键是从总体上看完成这件事情是“分类”完成,还是“分步”完成。“分类”完成用分类加法计数原理;“分步”完成用分步乘法计数原理。
例2:用0,1,2,3,4这五个数字可以组成多少个无重复数字的:
(1)银行存折的四位密码?
(2)四位数?
(3)四位奇数?
解:(1)完成“组成无重复数字的四位密码”这件事,可以分四个步骤:
第一步 选取左边第一个位置上的数字,有5种选取方法;
第二步 选取左边第二个位置上的数字,有4种选取方法;
第三步 选取左边第三个位置上的数字,有3种选取方法;
第四步 选取左边第四个位置上的数字,有2种选取方法;
由分步乘法计数原理,可组成不同的四位密码共有
N=5×4×3×2=120(个)
解:(2)完成“组成无重复数字的四位数”这件事,可以分四个步骤:
第一步 从1,2,3,4中选取一个数字做千位数字,有4种不同的选取方法;
第二步 从1,2,3,4中剩余的三个数字和0共四个数字中选取一个数字做百位数字,有4种不同的选取方法;
第三步 从剩余的三个数字中选取一个数字做十位数字,有3种不同的选取方法;
第四步 从剩余的两个数字中选取一个数字做个位数字,有2种不同的选取方法;
由分步乘法计数原理,可组成不同的四位数共有
N=4×4×3×2=96(个)
(3)完成“组成无重复数字的四位奇数”这件事,有两类办法:
第一类办法 四位奇数的个位数字为1,这件事分三个步骤完成:
第一步 从2,3,4中选取一个数字做千位数字,有3种不同的选取方法;
第二步 从2,3,4中剩余的两个数字和0共三个数字中选取一个数字做百位数字,有3种不同的选取方法;
第三步 从剩余的两个数字中,选取一个数字做十位数字,有2种不同的选取方法;
由分步乘法计数原理,第一类的四位奇数共有
N1=3×3×2=18(个)
第二类办法 四位奇数的个位数字为3,这件事分三个步骤完成:
第一步 从1,2,4中选取一个数字做千位数字,有3种不同的选取方法;
第二步 从1,2,4中剩余的两个数字和0共三个数字中选取一个数字做百位数字,有3种不同的选取方法;
第三步 从剩余的两个数字中,选取一个数字做十位数字,有2种不同的选取方法;
由分步乘法计数原理,第二类的四位奇数共有
N2=3×3×2=18(个)
最后,由分类加法计数原理,符合条件的四位奇数共有
N=N1+N2=18+18=36(个)
例3.在所有的两位数中,个位数字大于十位数字的两位数共有多少个?
分析2: 按个位数字是2,3,4,5,6,7,8,9分成8类,在每一类中满足条件的两位数分别是
1个,2个,3个,4个,5个,6个,7 个,8 个.
则根据分类加法计数原理共有 1 +2 +3 +4 + 5 + 6 + 7 + 8 =36 (个).
分析1: 按十位数字是1,2,3,4,5,6,7,8分成8类,在每一类中满足条件的两位数分别是
8个,7个,6个,5个,4个,3个,2个,1个.
则根据分类加法计数原理共有 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36 (个)
思考:利用分类加法计数原理解 决问题应注意什么问题? 首先要根据问题的特点确定一个分类的标准,分类的标准并不唯一,但分类的过程中,标准必须一致。其次要做到不重不漏。
点评: 分类加法计数原理中的“分类”要全面, 不能遗漏; 也不能重复、交叉;“类”与“类之间是并列的、互斥的、独立的,也就是说,完成一件事情,每次只能选择其中的一类办法中的某一种方法。若完成某件事情有n类办法, 即它们两两的交为空集,这n类的并为全集。
分步乘法计数原理中的“分步”程序要正确。“步”与“步”之间是连续的,不间断的,缺一不可;但也不能重复、交叉;若完成某件事情需n步, 则必须且只需依次完成这n个步骤后,这件事情才算完成。
在运用“分类加法计数原理、分步乘法计数原理”处理具体应用题时,除要弄清是“分类”还是“分步”外,还要搞清楚“分类”或“分步”的具体标准。在“分类”或“分步”过程中,标准必须一致,才能保证不重复、不遗漏。
课堂练习:1、(1)一件工作可以用两种方法完成。有5个人会用第一种方法完成,另有4个人会用第二种方法完成。从这9个人中选出一个人来完成这件工作,不同的选法共有_____种;
(2)一个科技小组中有3名女同学,5名男同学。从中任选一名同学参加学科竞赛,共有不同的选派方法____种;若从中任选一名女同学和一名男同学参加学科竞赛,共有不同的选派方法_____种。2、一名学生做除法游戏。在一个红口袋中装着20张分别标有数1,2,...,20的红卡片中,从中任意取一张,把卡片上的数作为被除数;在另一个黄口袋中装有10张分别标有1,2,...,10得黄卡片,从中任意取一张,把卡片上的数作为除数。问他一共可以列出多少个不同的除法式子?3、从一个小组的6名学生中产生一名组长,一名学生代表,在下列条件下各有多少种不同的选法?(1)不允许兼职(2)允许兼职。4、有数字0,1,2,3这4个数字,可组成多少个:
(1)无重复数字的三位数?
(2)可以有重复数字的三位数?
(3)无重复数字的三位偶数?
2.如图,从甲地到乙地有2条路可通,从乙地到丙地有3条路可通;从甲地到丁地有4条路可通, 从丁地到丙地有2条路可通。从甲地到丙地共有多少种不同的走法?
甲地乙地丙地丁地 解:从总体上看,由甲到丙有两类不同的走法,
第一类, 由甲经乙去丙,又需分两步, 所以 m1 = 2×3 = 6 种不同的走法;
第二类, 由甲经丁去丙,也需分两步, 所以 m2 = 4×2 = 8 种不同的走法;
所以从甲地到丙地共有 N = 6 + 8 = 14 种不同的走法。
课堂小结 :
1. 本节课学习了哪些主要内容? 答: 分类加法计数原理和分步乘法计数原理。 2. 分类加法计数原理和分步乘法计数原理的共同点是什么?不同点什么? 答: 共同点是, 它们都是研究完成一件事情, 共有多少种不同的方法。
不同点是, 它们研究完成一件事情的方式不同, 分类加法计数原理是“分类”完成, 即任何一类办法中的任何一个方法都能完成这件事。分步乘法计数原理是“分步”完成, 即这些方法需要分步,各个步骤顺次相依,且每一步都完成了,才能完成这件事情。这也是本节课的重点。
探索研究
1 .如图,要给地图A、B、C、D四个区域分别涂上红、蓝、黄3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
解: 按地图A、B、C、D四个区域依次分四步完成,
第一步, m1 = 3 种,
第二步, m2 = 2 种,
第三步, m3 = 1 种,
第四步, m4 = 1 种,
所以根据分步乘法计数原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。
㈣ 课堂练习
1 .如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
问: 若用2色、4色等,结果又怎样呢? 答:它们的涂色方案种数分别是 0, 4×3×2×2 = 48种等。
谢谢指导
髙二实验部 王明华
课堂引入 张、黄、李、赵四位好朋友约定在寒假中要互寄贺年片一张,他们一共寄了多少张贺年片?
如果他们约定在寒假中每两人通话一次,以祝贺新年,那么,他们的通话次数一共有多少呢?
问题 1. 从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船。一天中,火车有4 班, 汽车有2班,轮船有3班。那么一天中乘坐这些交通工具从甲地到乙地共有多少种不同的走法?
分析: 从甲地到乙地有3类办法,
第一类办法, 乘火车,有4种方法;
第二类办法, 乘汽车,有2种方法;
第三类办法, 乘轮船, 有3种方法;
所以 从甲地到乙地共有 4 + 2 + 3 = 9 种方法。
分类加法计数原理 做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法。那么完成这件事共有
N=m1+m2+…+mn
种不同的方法。
问题2. 如图,由A村去B村的道路有3条,由B村去C村的道路有2条。从A村经B村去C村,共有多少种不同的走法?
A村B村C村北南中北南 分析: 从A村经 B村去C村有2步,
第一步, 由A村去B村有3种方法,
第二步, 由B村去C村有2种方法,
所以 从A村经 B村去C村共有 3 ×2 = 6 种不同的方法。
分步乘法计数原理 做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
N=m1×m2×…×mn
种不同的方法。
思考: 分类加法计数原理与分步乘法计数原理有何共同之处?它们的区别在哪里?1 两个原理都用来研究解决完成一件事情,共有多少种不同方法的问题。
2 区别在于:它们研究完成一件事情的方式不同。分类计数原理是“分类”完成,即各类方法中的任何一种都可以把这件事做完;而分步计数原理是“分步”完成,即每一个步骤中的任何一种方法都不能把这件事情做完,各个步骤顺次相依,只有把各个步骤依次完成,才能把这件事情做完。
例题
例 1 一个三层书架的上层放有5本不同的数学书,中间放有3本不同的语文书,下层放有2本不同的英语书。
(1)从书架上任取一本书,有多少种不同的取法?
(2)从书架上任取三本书,其中数学书、语文书、英语书各一本,有多少种不同的取法?
解:(1)从书架上任取一本书,有三类办法:
第一类办法 从书架上层任取一本数学书,有5种不同的方法;
第二类办法 从书架中层任取一本语文书,有3种不同的方法;
第三类办法 从书架下层任取一本英语书,有2种不同的方法.
只要从书架上任意取出一本书,任务即完成,由分类加法计数原理,不同的取法共有
N=5+3+2=10(种)
解:
(2)从书架上任取三本书,其中数学书、语文书、英语书各一本,可以分三个步骤完成:
第一步 从书架上任取一本数学书,有5种不同的方法;
第二步 从书架上任取一本语文书,有3种不同的方法;
第三步 从书架上任取一本英语书,有2种不同的方法;
由分步乘法计数原理,不同的取法共有
N=5×3×2=30(种)
所以从书架上任取三本书,其中数学书、语文书、英语书各一本,共有30种不同的取法。
总结: 解题的关键是从总体上看完成这件事情是“分类”完成,还是“分步”完成。“分类”完成用分类加法计数原理;“分步”完成用分步乘法计数原理。
例2:用0,1,2,3,4这五个数字可以组成多少个无重复数字的:
(1)银行存折的四位密码?
(2)四位数?
(3)四位奇数?
解:(1)完成“组成无重复数字的四位密码”这件事,可以分四个步骤:
第一步 选取左边第一个位置上的数字,有5种选取方法;
第二步 选取左边第二个位置上的数字,有4种选取方法;
第三步 选取左边第三个位置上的数字,有3种选取方法;
第四步 选取左边第四个位置上的数字,有2种选取方法;
由分步乘法计数原理,可组成不同的四位密码共有
N=5×4×3×2=120(个)
解:(2)完成“组成无重复数字的四位数”这件事,可以分四个步骤:
第一步 从1,2,3,4中选取一个数字做千位数字,有4种不同的选取方法;
第二步 从1,2,3,4中剩余的三个数字和0共四个数字中选取一个数字做百位数字,有4种不同的选取方法;
第三步 从剩余的三个数字中选取一个数字做十位数字,有3种不同的选取方法;
第四步 从剩余的两个数字中选取一个数字做个位数字,有2种不同的选取方法;
由分步乘法计数原理,可组成不同的四位数共有
N=4×4×3×2=96(个)
(3)完成“组成无重复数字的四位奇数”这件事,有两类办法:
第一类办法 四位奇数的个位数字为1,这件事分三个步骤完成:
第一步 从2,3,4中选取一个数字做千位数字,有3种不同的选取方法;
第二步 从2,3,4中剩余的两个数字和0共三个数字中选取一个数字做百位数字,有3种不同的选取方法;
第三步 从剩余的两个数字中,选取一个数字做十位数字,有2种不同的选取方法;
由分步乘法计数原理,第一类的四位奇数共有
N1=3×3×2=18(个)
第二类办法 四位奇数的个位数字为3,这件事分三个步骤完成:
第一步 从1,2,4中选取一个数字做千位数字,有3种不同的选取方法;
第二步 从1,2,4中剩余的两个数字和0共三个数字中选取一个数字做百位数字,有3种不同的选取方法;
第三步 从剩余的两个数字中,选取一个数字做十位数字,有2种不同的选取方法;
由分步乘法计数原理,第二类的四位奇数共有
N2=3×3×2=18(个)
最后,由分类加法计数原理,符合条件的四位奇数共有
N=N1+N2=18+18=36(个)
例3.在所有的两位数中,个位数字大于十位数字的两位数共有多少个?
分析2: 按个位数字是2,3,4,5,6,7,8,9分成8类,在每一类中满足条件的两位数分别是
1个,2个,3个,4个,5个,6个,7 个,8 个.
则根据分类加法计数原理共有 1 +2 +3 +4 + 5 + 6 + 7 + 8 =36 (个).
分析1: 按十位数字是1,2,3,4,5,6,7,8分成8类,在每一类中满足条件的两位数分别是
8个,7个,6个,5个,4个,3个,2个,1个.
则根据分类加法计数原理共有 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36 (个)
思考:利用分类加法计数原理解 决问题应注意什么问题? 首先要根据问题的特点确定一个分类的标准,分类的标准并不唯一,但分类的过程中,标准必须一致。其次要做到不重不漏。
点评: 分类加法计数原理中的“分类”要全面, 不能遗漏; 也不能重复、交叉;“类”与“类之间是并列的、互斥的、独立的,也就是说,完成一件事情,每次只能选择其中的一类办法中的某一种方法。若完成某件事情有n类办法, 即它们两两的交为空集,这n类的并为全集。
分步乘法计数原理中的“分步”程序要正确。“步”与“步”之间是连续的,不间断的,缺一不可;但也不能重复、交叉;若完成某件事情需n步, 则必须且只需依次完成这n个步骤后,这件事情才算完成。
在运用“分类加法计数原理、分步乘法计数原理”处理具体应用题时,除要弄清是“分类”还是“分步”外,还要搞清楚“分类”或“分步”的具体标准。在“分类”或“分步”过程中,标准必须一致,才能保证不重复、不遗漏。
课堂练习:1、(1)一件工作可以用两种方法完成。有5个人会用第一种方法完成,另有4个人会用第二种方法完成。从这9个人中选出一个人来完成这件工作,不同的选法共有_____种;
(2)一个科技小组中有3名女同学,5名男同学。从中任选一名同学参加学科竞赛,共有不同的选派方法____种;若从中任选一名女同学和一名男同学参加学科竞赛,共有不同的选派方法_____种。2、一名学生做除法游戏。在一个红口袋中装着20张分别标有数1,2,...,20的红卡片中,从中任意取一张,把卡片上的数作为被除数;在另一个黄口袋中装有10张分别标有1,2,...,10得黄卡片,从中任意取一张,把卡片上的数作为除数。问他一共可以列出多少个不同的除法式子?3、从一个小组的6名学生中产生一名组长,一名学生代表,在下列条件下各有多少种不同的选法?(1)不允许兼职(2)允许兼职。4、有数字0,1,2,3这4个数字,可组成多少个:
(1)无重复数字的三位数?
(2)可以有重复数字的三位数?
(3)无重复数字的三位偶数?
2.如图,从甲地到乙地有2条路可通,从乙地到丙地有3条路可通;从甲地到丁地有4条路可通, 从丁地到丙地有2条路可通。从甲地到丙地共有多少种不同的走法?
甲地乙地丙地丁地 解:从总体上看,由甲到丙有两类不同的走法,
第一类, 由甲经乙去丙,又需分两步, 所以 m1 = 2×3 = 6 种不同的走法;
第二类, 由甲经丁去丙,也需分两步, 所以 m2 = 4×2 = 8 种不同的走法;
所以从甲地到丙地共有 N = 6 + 8 = 14 种不同的走法。
课堂小结 :
1. 本节课学习了哪些主要内容? 答: 分类加法计数原理和分步乘法计数原理。 2. 分类加法计数原理和分步乘法计数原理的共同点是什么?不同点什么? 答: 共同点是, 它们都是研究完成一件事情, 共有多少种不同的方法。
不同点是, 它们研究完成一件事情的方式不同, 分类加法计数原理是“分类”完成, 即任何一类办法中的任何一个方法都能完成这件事。分步乘法计数原理是“分步”完成, 即这些方法需要分步,各个步骤顺次相依,且每一步都完成了,才能完成这件事情。这也是本节课的重点。
探索研究
1 .如图,要给地图A、B、C、D四个区域分别涂上红、蓝、黄3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
解: 按地图A、B、C、D四个区域依次分四步完成,
第一步, m1 = 3 种,
第二步, m2 = 2 种,
第三步, m3 = 1 种,
第四步, m4 = 1 种,
所以根据分步乘法计数原理, 得到不同的涂色方案种数共有 N = 3 × 2 ×1×1 = 6 种。
㈣ 课堂练习
1 .如图,要给地图A、B、C、D四个区域分别涂上3种不同颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有多少种?
问: 若用2色、4色等,结果又怎样呢? 答:它们的涂色方案种数分别是 0, 4×3×2×2 = 48种等。
谢谢指导
髙二实验部 王明华
