第24章圆期末复习(1)旋转课件(共25张PPT)
文档属性
| 名称 | 第24章圆期末复习(1)旋转课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 21:11:06 | ||
图片预览




文档简介
(共25张PPT)
第24章 圆 期末复习(1)
沪科版
旋转
θ
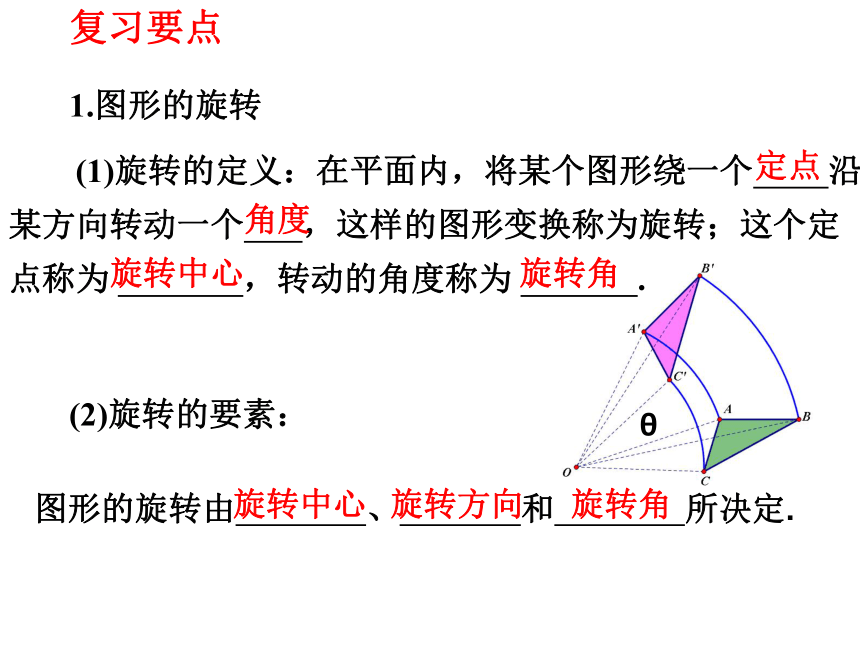
图形的旋转由 、 和 所决定.
(1)旋转的定义:在平面内,将某个图形绕一个 沿某方向转动一个 ,这样的图形变换称为旋转;这个定点称为 ,转动的角度称为 .
1.图形的旋转
(2)旋转的要素:
定点
角度
旋转中心
旋转角
旋转中心
旋转方向
旋转角
复习要点
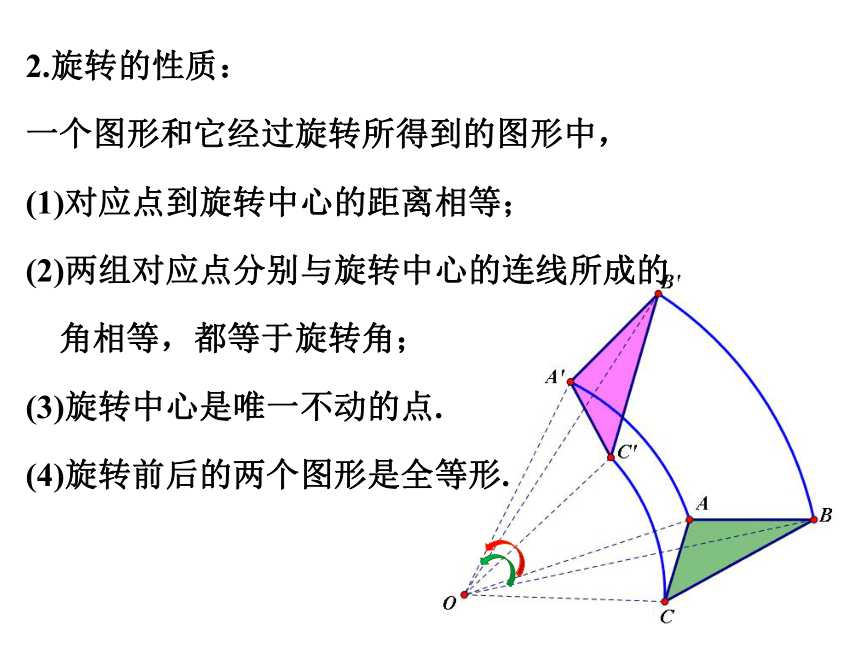
2.旋转的性质:
一个图形和它经过旋转所得到的图形中,
(1)对应点到旋转中心的距离相等;
(2)两组对应点分别与旋转中心的连线所成的
角相等,都等于旋转角;
(3)旋转中心是唯一不动的点.
(4)旋转前后的两个图形是全等形.
一个图形只要满足绕一点旋转后能与原图形重合
这一条件,就是旋转对称图形.
3. 旋转对称图形.
在平面直角坐标系中,点P(x,y)关于原点
O对称的点P‘的坐标为(-x ,-y ).
4.关于原点对称的点的坐标特征
5.旋转作图
(1)旋转作图的依据是旋转的特征.
(2)旋转作图的步骤如下:
①确定旋转中心、旋转方向和旋转角度;
②确定图形的关键点(如三角形的三个顶点);
③将这些关键点沿旋转方向转动一定的角度;
④按照原图形的连结方式,顺次连结这些对应点,
得到旋转后的图形.
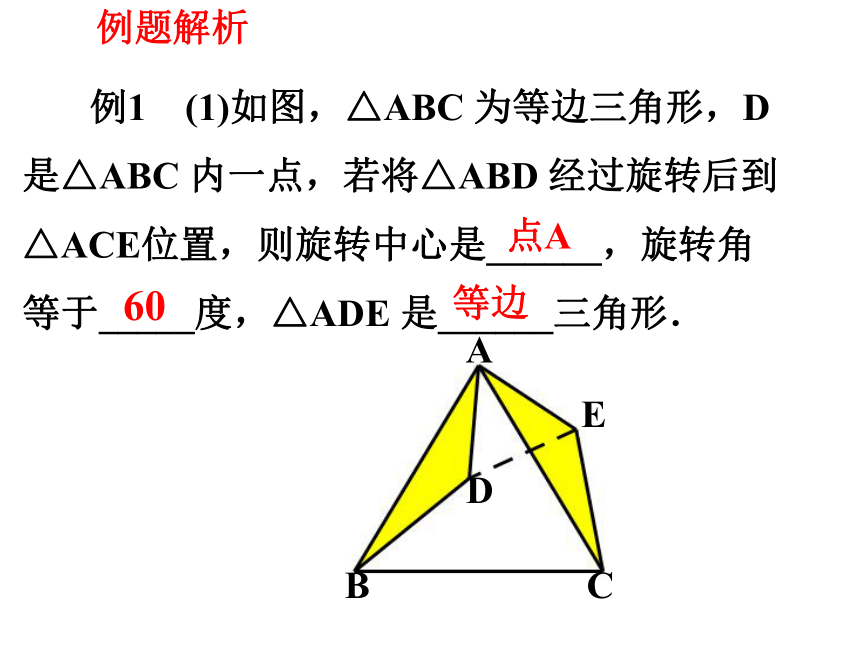
例1 (1)如图,△ABC 为等边三角形,D 是△ABC 内一点,若将△ABD 经过旋转后到△ACE位置,则旋转中心是______,旋转角等于_____度,△ADE 是______三角形.
A
B
D
E
C
例题解析
点A
60
等边
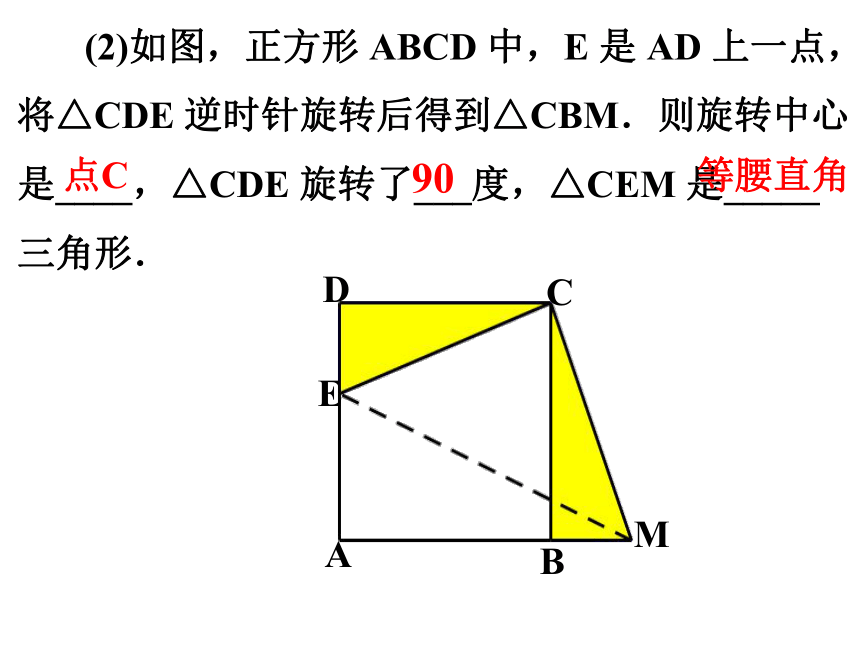
(2)如图,正方形 ABCD 中,E 是 AD 上一点,
将△CDE 逆时针旋转后得到△CBM.则旋转中心是____,△CDE 旋转了___度,△CEM 是_____
三角形.
D
A
E
B
C
M
点C
90
等腰直角
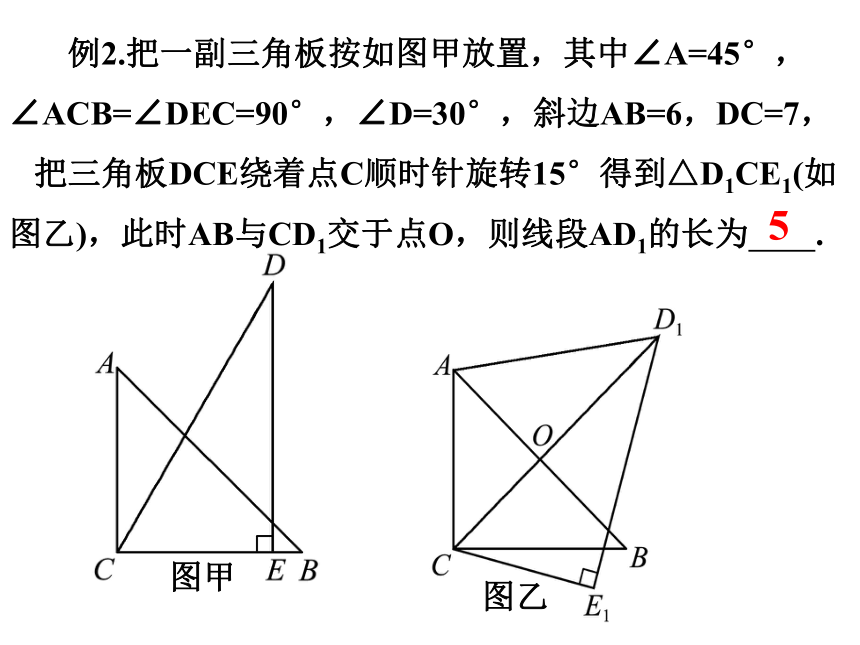
例2.把一副三角板按如图甲放置,其中∠A=45°,∠ACB=∠DEC=90°,∠D=30°,斜边AB=6,DC=7,
把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为 .
图甲
图乙
5
∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°-30°=60°,
∴∠ACD=90°-60°=30°,
∵旋转角为15°,
∴∠ACD1=30°+15°=45°.
∵∠CAB=45°,
∴ △ACO是等腰直角三角形,
∴AO=CO=AB= ×6=3,AB⊥CO.
∵DC=7,∴D1C=DC=7,
∴D1O=7-3=4,
在Rt△AOD1中,AD1=5.
图乙
例3.如图,△ABO 与△CDO 关于点O成中心对称,
点EF在线段AC上,且AF=CE.求证: DF=BE.
A
D
B
C
O
E
F
证明:
∵△ABO 与△CDO 关于点O成中心对称,
∴△ABO ≌△CDO.
∴AO =CO,
BO =DO,
∠AOB =∠COD.
∴∠EOB=∠FOD.
∵AF=CE,
∴FO=EO.
∴△BOE ≌△DOF
∴DF=BE.
(SAS).
1.下列图形中,既是轴对称图形,又是中心对 称图形的是( ).
A. B. C. D.
D
练习巩固
2.下列图形中,是中心对称图形但不是轴对称图形的是( ).
B
3.五星红旗上的每一个五角星( ).
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
A
4.如图,在 Rt△ ACB中, ∠B=60°,将△ Rt△ ACB绕点 A逆时针旋转70°后得到△AC′B′,则∠ CAB′=( ).
A. 60° B. 70°
C. 100° D. 120°
A
B
C
C′
B′
C
5.如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( ).
A.30° B.35° C.40° D.50°
A
6.如图,△ ABC以点 O为旋转中心,旋转180°后得到△A′B′C′. ED是△ABC 的中位线,经旋转后为线段E′D′. 已知BC=6 ,则 E′D′= ( ).
A.3 B.4 C.4.5 D.5
.
D′
A
B
C
D
E
A′
B′
C′
E′
O
A
7.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( ).
A.60° B.75°
C.85° D.90°
C
8.在平面直角坐标系中,线段OP的两个端点坐标分别是O(0,0),P(6,8),将线段OP绕点O逆时针旋转90°到OP′位置,则点P′的坐标为( ).
A.(8,6) B.(-6,8)
C.(-8,6) D.(6,-8)
C
9.在平面直角坐标系中,点P(-3,2)关于原点
O对称的点P'的坐标为( ).
A.(3,2) B.(2, -3)
C.(-3,-2) D.(3,-2)
D
10.如图,Rt△ABO的点A的坐标是(6,4),将△ABO绕原点O按逆时针方向旋转90°,得到△A′B′O ,则点A的对应点 A′的坐标是 .
A
(6,4)
B
O
A′
B′
x
y
(-4, 6)
11.如图,在△ABC中,∠A=70°,AC=BC,以点B为旋转中心把 △ABC按顺时针旋转α度,得到△A′BC′,点A恰好落在AC上,连接 CC′,
则∠ACC′= .
A
B
C
C′
A′
α
110°
12.如图,在 Rt△ABC中, ∠C=90°,∠ABC=30° , AC=1.将 Rt△ABC绕点A逆时针旋转 30°后得到△AB′C′,则图中阴影部分的面积是 .
A
B
C
D
B′
C′
3
π
-
3
13. 如图,在矩形ABCD中,AB=6,BC=8,以D为旋转中心,顺时针旋转180°后停止,矩形ABCD在旋转过程中所扫过的面积是 .
。
A
B
C
D
50π+48
A
y
x
B
O
C
14.如图 ,在平面直角坐标系中,点A与点B 的坐
标分别为(2,0), (0,1).AC由AB绕点A顺时
针旋转90°而得,则AC所在直线的函数表达
式是 .
(3 ,2)
(2 ,0)
2k+b=0
3k+b=2
k=2
b=-4
y=2x-4
15.已知:△ABC 中,A(-2,4),B(-4,1), C(-1, -2).请画出△ABC 关于原点 O 对称的△A1B1C1.
A
y
x
B
O
C
A1
B1
C1
第24章 圆 期末复习(1)
沪科版
旋转
θ
图形的旋转由 、 和 所决定.
(1)旋转的定义:在平面内,将某个图形绕一个 沿某方向转动一个 ,这样的图形变换称为旋转;这个定点称为 ,转动的角度称为 .
1.图形的旋转
(2)旋转的要素:
定点
角度
旋转中心
旋转角
旋转中心
旋转方向
旋转角
复习要点
2.旋转的性质:
一个图形和它经过旋转所得到的图形中,
(1)对应点到旋转中心的距离相等;
(2)两组对应点分别与旋转中心的连线所成的
角相等,都等于旋转角;
(3)旋转中心是唯一不动的点.
(4)旋转前后的两个图形是全等形.
一个图形只要满足绕一点旋转后能与原图形重合
这一条件,就是旋转对称图形.
3. 旋转对称图形.
在平面直角坐标系中,点P(x,y)关于原点
O对称的点P‘的坐标为(-x ,-y ).
4.关于原点对称的点的坐标特征
5.旋转作图
(1)旋转作图的依据是旋转的特征.
(2)旋转作图的步骤如下:
①确定旋转中心、旋转方向和旋转角度;
②确定图形的关键点(如三角形的三个顶点);
③将这些关键点沿旋转方向转动一定的角度;
④按照原图形的连结方式,顺次连结这些对应点,
得到旋转后的图形.
例1 (1)如图,△ABC 为等边三角形,D 是△ABC 内一点,若将△ABD 经过旋转后到△ACE位置,则旋转中心是______,旋转角等于_____度,△ADE 是______三角形.
A
B
D
E
C
例题解析
点A
60
等边
(2)如图,正方形 ABCD 中,E 是 AD 上一点,
将△CDE 逆时针旋转后得到△CBM.则旋转中心是____,△CDE 旋转了___度,△CEM 是_____
三角形.
D
A
E
B
C
M
点C
90
等腰直角
例2.把一副三角板按如图甲放置,其中∠A=45°,∠ACB=∠DEC=90°,∠D=30°,斜边AB=6,DC=7,
把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为 .
图甲
图乙
5
∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°-30°=60°,
∴∠ACD=90°-60°=30°,
∵旋转角为15°,
∴∠ACD1=30°+15°=45°.
∵∠CAB=45°,
∴ △ACO是等腰直角三角形,
∴AO=CO=AB= ×6=3,AB⊥CO.
∵DC=7,∴D1C=DC=7,
∴D1O=7-3=4,
在Rt△AOD1中,AD1=5.
图乙
例3.如图,△ABO 与△CDO 关于点O成中心对称,
点EF在线段AC上,且AF=CE.求证: DF=BE.
A
D
B
C
O
E
F
证明:
∵△ABO 与△CDO 关于点O成中心对称,
∴△ABO ≌△CDO.
∴AO =CO,
BO =DO,
∠AOB =∠COD.
∴∠EOB=∠FOD.
∵AF=CE,
∴FO=EO.
∴△BOE ≌△DOF
∴DF=BE.
(SAS).
1.下列图形中,既是轴对称图形,又是中心对 称图形的是( ).
A. B. C. D.
D
练习巩固
2.下列图形中,是中心对称图形但不是轴对称图形的是( ).
B
3.五星红旗上的每一个五角星( ).
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
A
4.如图,在 Rt△ ACB中, ∠B=60°,将△ Rt△ ACB绕点 A逆时针旋转70°后得到△AC′B′,则∠ CAB′=( ).
A. 60° B. 70°
C. 100° D. 120°
A
B
C
C′
B′
C
5.如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( ).
A.30° B.35° C.40° D.50°
A
6.如图,△ ABC以点 O为旋转中心,旋转180°后得到△A′B′C′. ED是△ABC 的中位线,经旋转后为线段E′D′. 已知BC=6 ,则 E′D′= ( ).
A.3 B.4 C.4.5 D.5
.
D′
A
B
C
D
E
A′
B′
C′
E′
O
A
7.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,若∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( ).
A.60° B.75°
C.85° D.90°
C
8.在平面直角坐标系中,线段OP的两个端点坐标分别是O(0,0),P(6,8),将线段OP绕点O逆时针旋转90°到OP′位置,则点P′的坐标为( ).
A.(8,6) B.(-6,8)
C.(-8,6) D.(6,-8)
C
9.在平面直角坐标系中,点P(-3,2)关于原点
O对称的点P'的坐标为( ).
A.(3,2) B.(2, -3)
C.(-3,-2) D.(3,-2)
D
10.如图,Rt△ABO的点A的坐标是(6,4),将△ABO绕原点O按逆时针方向旋转90°,得到△A′B′O ,则点A的对应点 A′的坐标是 .
A
(6,4)
B
O
A′
B′
x
y
(-4, 6)
11.如图,在△ABC中,∠A=70°,AC=BC,以点B为旋转中心把 △ABC按顺时针旋转α度,得到△A′BC′,点A恰好落在AC上,连接 CC′,
则∠ACC′= .
A
B
C
C′
A′
α
110°
12.如图,在 Rt△ABC中, ∠C=90°,∠ABC=30° , AC=1.将 Rt△ABC绕点A逆时针旋转 30°后得到△AB′C′,则图中阴影部分的面积是 .
A
B
C
D
B′
C′
3
π
-
3
13. 如图,在矩形ABCD中,AB=6,BC=8,以D为旋转中心,顺时针旋转180°后停止,矩形ABCD在旋转过程中所扫过的面积是 .
。
A
B
C
D
50π+48
A
y
x
B
O
C
14.如图 ,在平面直角坐标系中,点A与点B 的坐
标分别为(2,0), (0,1).AC由AB绕点A顺时
针旋转90°而得,则AC所在直线的函数表达
式是 .
(3 ,2)
(2 ,0)
2k+b=0
3k+b=2
k=2
b=-4
y=2x-4
15.已知:△ABC 中,A(-2,4),B(-4,1), C(-1, -2).请画出△ABC 关于原点 O 对称的△A1B1C1.
A
y
x
B
O
C
A1
B1
C1
