第24章圆期末复习(2)圆的基本性质课件(共26张PPT)
文档属性
| 名称 | 第24章圆期末复习(2)圆的基本性质课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 601.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 21:17:39 | ||
图片预览






文档简介
(共26张PPT)
第24章 圆 期末复习(2)
沪科版
圆的基本性质
1.圆
(1)平面上到定点的 等于定长的所有 组成的图形叫做圆; 称为圆心, 称为半径.
(2)圆是轴对称图形,其对称轴是任意一条过 的直线;圆又是中心对称图形,对称中心是 .
(3)不在同一条直线上的 点确定一个圆.
距离
点
定点
定长
圆心
圆心
三个
复习要点
2.弧、弦
(1)圆上任意 间的部分叫做弧.
(2)连接圆上任意两点的 叫做弦,经过 的弦叫做直径.
(3)垂直于弦的 平分这条弦,并且平分弦所对的两条 .
(4)平分弦 (不是 )的直径垂直于 ,并且平分弦所对的两条 .
两点
线段
圆心
直径
弧
直径
弦
弧
3.弧、弦、圆心角的关系
(1)在同圆或等圆中,相等的 所对的弧相等,所对的弦相等.
(2)在同圆或等圆中,如果两个圆心角、两条 、两条 中有一组量相等,那么它们所对的其余各组量都分别相等.
圆心角
弧
弦
4.圆周角与圆心角
(1)顶点在圆上,两条边分别与圆 的角叫做圆周角.
(2)在同圆或等圆中,同弧或等弧所对的圆周角 .
(3)直径所对的 角是直角,
的圆周角所对的弦是直径.
(4)一条弧所对的圆周角等于它所对的 角的一半.
相交
相等
圆周
90°
圆心
5.三角形的外接圆
(1)三角形的三个 所确定的圆叫做三角形的外接圆;外接圆的圆心是三角形三边 的交点,叫做三角形的 .
(2)圆内接四边形的对角 ,且任何一个外角都
等于它的内对角.
顶点
垂直平分线
外心
互补
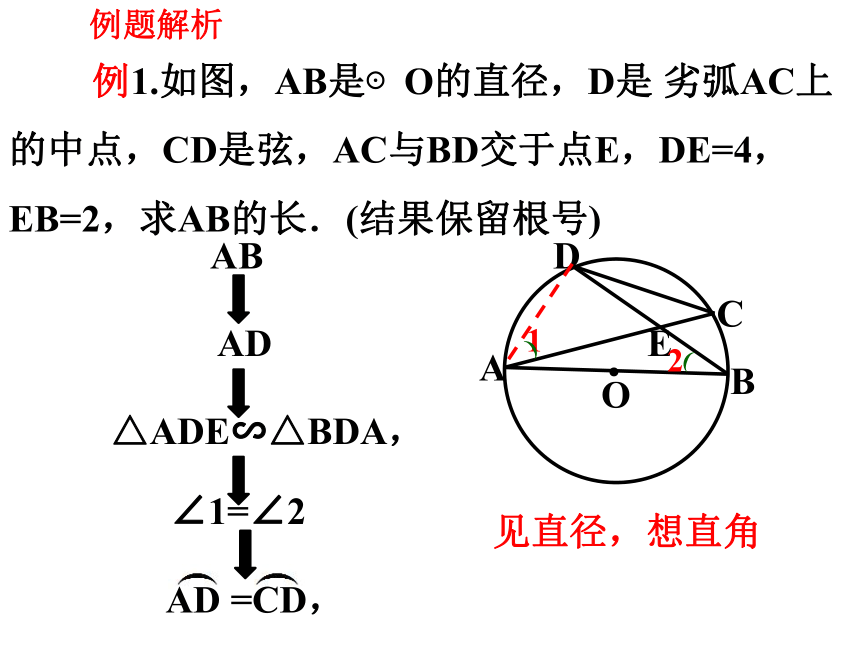
例1.如图,AB是⊙O的直径,D是 劣弧AC上的中点,CD是弦,AC与BD交于点E,DE=4,EB=2,求AB的长.(结果保留根号)
●
O
D
E
C
B
A
见直径,想直角
AB
△ADE∽△BDA,
1
2
∠1=∠2
AD =CD,
AD
)
)
例题解析
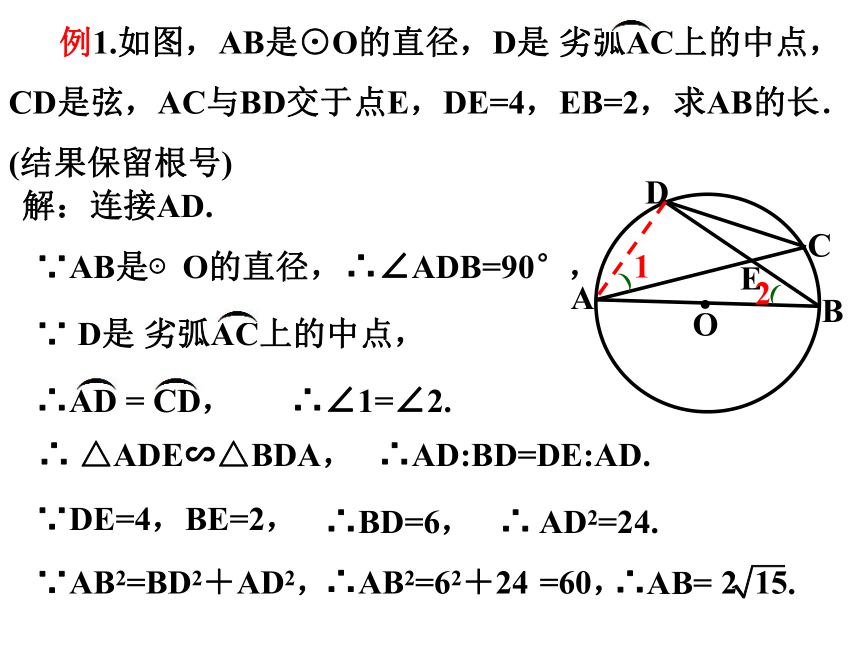
例1.如图,AB是⊙O的直径,D是 劣弧AC上的中点,CD是弦,AC与BD交于点E,DE=4,EB=2,求AB的长.
(结果保留根号)
●
O
D
E
C
B
A
解:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD = CD,
∴∠1=∠2.
∴ △ADE∽△BDA,
∴AD:BD=DE:AD.
∵DE=4,BE=2,
∴BD=6,
∴ AD2=24.
∵AB2=BD2+AD2,
∴AB2=62+24
=60,
∴AB= .
15
2
)
)
1
2
∵ D是 劣弧AC上的中点,
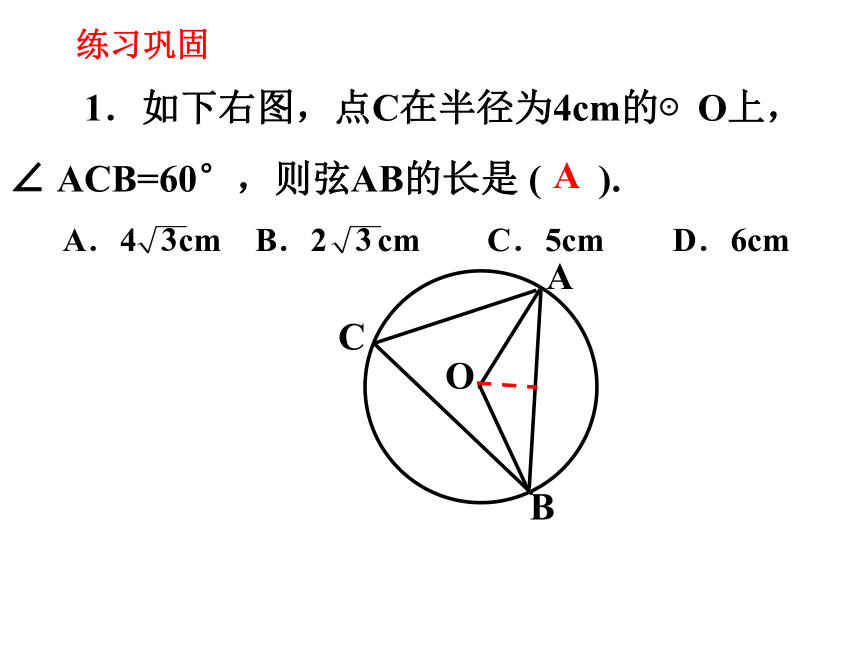
1.如下右图,点C在半径为4cm的⊙O上,
∠ ACB=60°,则弦AB的长是 ( ).
A
C
O
B
A.4 cm B.2 cm C.5cm D.6cm
3
3
A
练习巩固
·
D
A
C
B
O
E
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论一定正确的个数有 ( ).
①CE=DE;②BE=OE;③ CB=BD ;
④∠CAB=∠DAB;⑤AC=AD.
A.4个 B.3个 C.2个 D.1个
︵
︵
A
3. 如下左图,在⊙O中,若∠AOB=120°,则∠C的度数是 ( ).
A. 70° B. 65° C. 60° D. 50°
A
B
C
O
C
4.如图,AB是⊙O的直径,AB垂直于
弦CD, ∠BOC=70°,则∠ABD= ( ).
A.20° B.46° C.55° D.70°
A
B
C
O
D
C
5.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD,若∠DOB=140°,则∠ACD= ( ).
A.20° B. 30° C. 40° D.70°
A
B
C
D
O
A
6.如图,⊙O的直径CD过弦EF的中点G, 连接CF,∠C=30°,CF= ,则OG的长是( ).
A.1 B. C. 2 D.
3
2
2
2
3
A
7.如图,已知四边形ABCD 内接于⊙O ,直径AC=6 ,对角线AC 、BD交于点E,且AB=BD,EC=1 ,则 AD的长为 ( ).
A. B. C. D.
A
B
C
D
O
E
17
3
11
2
2
3
2
15
3
A
1
AD
△CDE∽△OBE,
∠1=∠2
CD
CD ∥ BO
2
)
)
BO⊥AD
8.如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:①若AC=AB,则DE=CE;②若∠C=45°,记△CDE的面积为S1,四边形DABE的面积为S2,则S1=S2,那么( ).
A.①是真命题 ②是假命题
B.①是假命题 ②是真命题
C.①是假命题 ②是假命题
D.①是真命题 ②是真命题
A
C
B
D
O
E
D
9.如图,在半径为 的⊙O中,弦AB与CD交于点E, ∠DEB=75°,AB=6,AE=1,则CD的长是( ).
A. B. C. D.
6
2
10
2
11
2
3
4
13
O
A
B
C
D
E
G
F
C
10.如图, ⊙O是△ABC的外接圆,且AB=AC, ∠ BAC=36°,在AB上取点D(不与点A,B重合),连接BD,AD,则∠BAD+
∠ ABD的度数是( ).
A.60° B.62°
C.72° D. 73°
A
B
C
O
D
C
11.已知⊙O的半径为13cm,弦AB//CD,
AB=24cm,CD=10cm,则AB、CD之间的
距离为( ).
A.17cm B.7 cm
C.12 cm D.7 cm或17 cm
图(1) 图(2)
D
D
B
A
O
C
12.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为 m.
4
13.如下左图, AB是⊙O的直径,点 C在⊙O上, ∠COB =58°,则∠CAB= .
A
B
C
O
29°
14.如图,已知在⊙O 中,半径 OA= ,弦 AB=2,∠BAD=18°,OD 与AB 交于点 C,则∠ACO= 度
2
81
A
B
C
D
O
15.如图,MN是⊙O的弦,正方形OABC的顶点B,C在MN上,且点B是CM的中点.若正方形OABC的边长为7,则MN的长为 .
A
B
C
M
O
N
28
16.如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD于点M点.
求证:(1)△ACO≌△BDO;(2)CE=DF.
A
B
C
D
E
F
O
M
16.如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD于点M.求证:(1)△ACO≌△BDO;
A
B
C
D
E
F
O
M
证明:(1)
∵ AC、DB分别切⊙O于A、B两点,
∴AO⊥AC,OB⊥BD,
∴∠A=∠B= 90°.
∵OA=OB,
∠AOC=∠BOD,
∴△ACO≌△BDO(ASA).
16.如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD于点M.
求证: (2)CE=DF.
A
B
C
D
E
F
O
M
∴OC=OD,
∵△ACO≌△BDO,
(2)
∵OM⊥CD,
∴CM=DM,
EM=FM,
∴CM-EM=DM-FM.
∴CE=DF.
第24章 圆 期末复习(2)
沪科版
圆的基本性质
1.圆
(1)平面上到定点的 等于定长的所有 组成的图形叫做圆; 称为圆心, 称为半径.
(2)圆是轴对称图形,其对称轴是任意一条过 的直线;圆又是中心对称图形,对称中心是 .
(3)不在同一条直线上的 点确定一个圆.
距离
点
定点
定长
圆心
圆心
三个
复习要点
2.弧、弦
(1)圆上任意 间的部分叫做弧.
(2)连接圆上任意两点的 叫做弦,经过 的弦叫做直径.
(3)垂直于弦的 平分这条弦,并且平分弦所对的两条 .
(4)平分弦 (不是 )的直径垂直于 ,并且平分弦所对的两条 .
两点
线段
圆心
直径
弧
直径
弦
弧
3.弧、弦、圆心角的关系
(1)在同圆或等圆中,相等的 所对的弧相等,所对的弦相等.
(2)在同圆或等圆中,如果两个圆心角、两条 、两条 中有一组量相等,那么它们所对的其余各组量都分别相等.
圆心角
弧
弦
4.圆周角与圆心角
(1)顶点在圆上,两条边分别与圆 的角叫做圆周角.
(2)在同圆或等圆中,同弧或等弧所对的圆周角 .
(3)直径所对的 角是直角,
的圆周角所对的弦是直径.
(4)一条弧所对的圆周角等于它所对的 角的一半.
相交
相等
圆周
90°
圆心
5.三角形的外接圆
(1)三角形的三个 所确定的圆叫做三角形的外接圆;外接圆的圆心是三角形三边 的交点,叫做三角形的 .
(2)圆内接四边形的对角 ,且任何一个外角都
等于它的内对角.
顶点
垂直平分线
外心
互补
例1.如图,AB是⊙O的直径,D是 劣弧AC上的中点,CD是弦,AC与BD交于点E,DE=4,EB=2,求AB的长.(结果保留根号)
●
O
D
E
C
B
A
见直径,想直角
AB
△ADE∽△BDA,
1
2
∠1=∠2
AD =CD,
AD
)
)
例题解析
例1.如图,AB是⊙O的直径,D是 劣弧AC上的中点,CD是弦,AC与BD交于点E,DE=4,EB=2,求AB的长.
(结果保留根号)
●
O
D
E
C
B
A
解:连接AD.
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD = CD,
∴∠1=∠2.
∴ △ADE∽△BDA,
∴AD:BD=DE:AD.
∵DE=4,BE=2,
∴BD=6,
∴ AD2=24.
∵AB2=BD2+AD2,
∴AB2=62+24
=60,
∴AB= .
15
2
)
)
1
2
∵ D是 劣弧AC上的中点,
1.如下右图,点C在半径为4cm的⊙O上,
∠ ACB=60°,则弦AB的长是 ( ).
A
C
O
B
A.4 cm B.2 cm C.5cm D.6cm
3
3
A
练习巩固
·
D
A
C
B
O
E
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论一定正确的个数有 ( ).
①CE=DE;②BE=OE;③ CB=BD ;
④∠CAB=∠DAB;⑤AC=AD.
A.4个 B.3个 C.2个 D.1个
︵
︵
A
3. 如下左图,在⊙O中,若∠AOB=120°,则∠C的度数是 ( ).
A. 70° B. 65° C. 60° D. 50°
A
B
C
O
C
4.如图,AB是⊙O的直径,AB垂直于
弦CD, ∠BOC=70°,则∠ABD= ( ).
A.20° B.46° C.55° D.70°
A
B
C
O
D
C
5.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD,若∠DOB=140°,则∠ACD= ( ).
A.20° B. 30° C. 40° D.70°
A
B
C
D
O
A
6.如图,⊙O的直径CD过弦EF的中点G, 连接CF,∠C=30°,CF= ,则OG的长是( ).
A.1 B. C. 2 D.
3
2
2
2
3
A
7.如图,已知四边形ABCD 内接于⊙O ,直径AC=6 ,对角线AC 、BD交于点E,且AB=BD,EC=1 ,则 AD的长为 ( ).
A. B. C. D.
A
B
C
D
O
E
17
3
11
2
2
3
2
15
3
A
1
AD
△CDE∽△OBE,
∠1=∠2
CD
CD ∥ BO
2
)
)
BO⊥AD
8.如图,AB是⊙O的直径,AC,BC分别与⊙O相交于点D,E,连接DE,现给出两个命题:①若AC=AB,则DE=CE;②若∠C=45°,记△CDE的面积为S1,四边形DABE的面积为S2,则S1=S2,那么( ).
A.①是真命题 ②是假命题
B.①是假命题 ②是真命题
C.①是假命题 ②是假命题
D.①是真命题 ②是真命题
A
C
B
D
O
E
D
9.如图,在半径为 的⊙O中,弦AB与CD交于点E, ∠DEB=75°,AB=6,AE=1,则CD的长是( ).
A. B. C. D.
6
2
10
2
11
2
3
4
13
O
A
B
C
D
E
G
F
C
10.如图, ⊙O是△ABC的外接圆,且AB=AC, ∠ BAC=36°,在AB上取点D(不与点A,B重合),连接BD,AD,则∠BAD+
∠ ABD的度数是( ).
A.60° B.62°
C.72° D. 73°
A
B
C
O
D
C
11.已知⊙O的半径为13cm,弦AB//CD,
AB=24cm,CD=10cm,则AB、CD之间的
距离为( ).
A.17cm B.7 cm
C.12 cm D.7 cm或17 cm
图(1) 图(2)
D
D
B
A
O
C
12.某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为 m.
4
13.如下左图, AB是⊙O的直径,点 C在⊙O上, ∠COB =58°,则∠CAB= .
A
B
C
O
29°
14.如图,已知在⊙O 中,半径 OA= ,弦 AB=2,∠BAD=18°,OD 与AB 交于点 C,则∠ACO= 度
2
81
A
B
C
D
O
15.如图,MN是⊙O的弦,正方形OABC的顶点B,C在MN上,且点B是CM的中点.若正方形OABC的边长为7,则MN的长为 .
A
B
C
M
O
N
28
16.如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD于点M点.
求证:(1)△ACO≌△BDO;(2)CE=DF.
A
B
C
D
E
F
O
M
16.如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD于点M.求证:(1)△ACO≌△BDO;
A
B
C
D
E
F
O
M
证明:(1)
∵ AC、DB分别切⊙O于A、B两点,
∴AO⊥AC,OB⊥BD,
∴∠A=∠B= 90°.
∵OA=OB,
∠AOC=∠BOD,
∴△ACO≌△BDO(ASA).
16.如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD于点M.
求证: (2)CE=DF.
A
B
C
D
E
F
O
M
∴OC=OD,
∵△ACO≌△BDO,
(2)
∵OM⊥CD,
∴CM=DM,
EM=FM,
∴CM-EM=DM-FM.
∴CE=DF.
