第24章圆期末复习(3)圆与直线的位置关系课件(共28张PPT)
文档属性
| 名称 | 第24章圆期末复习(3)圆与直线的位置关系课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 767.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 18:11:09 | ||
图片预览






文档简介
(共28张PPT)
第24章 圆 期末复习(3)
沪科版
圆与直线的位置关系
如果圆的半径是r,点到圆心的距离为d,那么:
(1)点在圆外 d r;
(2)点在圆上 d r;
(3)点在圆内 d r。
1.点和圆的位置关系:
点和圆的位置关系有: 、 和
.
点在圆外
点在圆内
点在圆上
>
=
<
复习要点
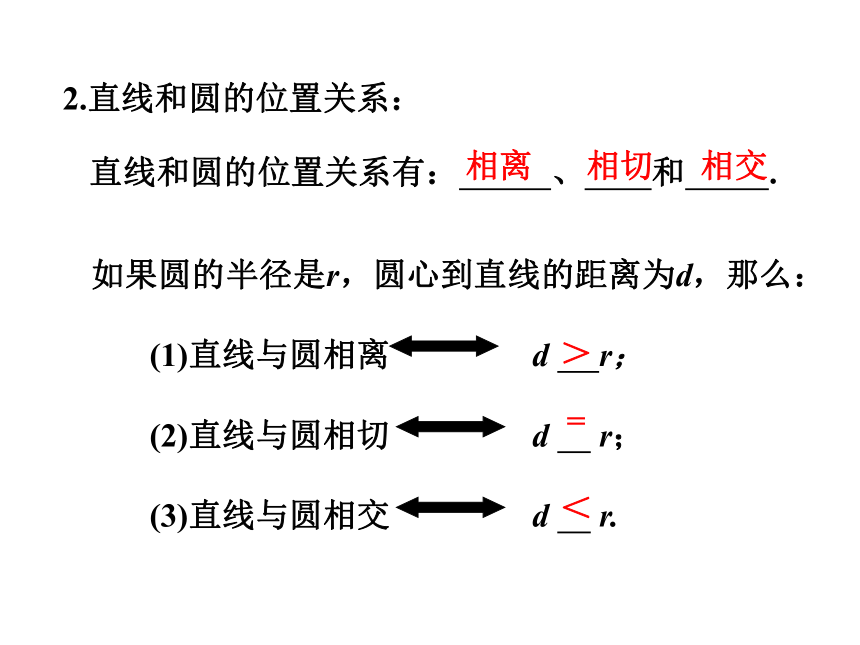
如果圆的半径是r,圆心到直线的距离为d,那么:
(1)直线与圆相离 d r;
(2)直线与圆相切 d r;
(3)直线与圆相交 d r.
2.直线和圆的位置关系:
直线和圆的位置关系有: 、 和 .
相离
相交
相切
>
=
<
直线和圆只有 公共点时,这条直线叫做圆的切线;这个唯一的公共点叫做 .
5.圆的切线的性质
圆的切线垂直于过切点的 ;
6.圆的切线的判定
经过直径的 ,并且 这条的直线是圆的切线.
4.圆的切线的定义
一个
切点
半径
外端
垂直于
7.切线长
经过圆外一点作圆的切线,这点和 之间的线段的长,叫做这点到圆的切线长。从圆外一点可以作出 条圆的切线,它们的切线长 ;这点与圆心的连线 两切线的夹角.
8.三角形内切圆
和三角形各边都 的圆叫做三角形的内切圆,内切圆的圆心是三角形三条 的交点,它到三边的距离相等,叫做三角形的 心.
切点
两
相等
平分
相切
角平分线
内
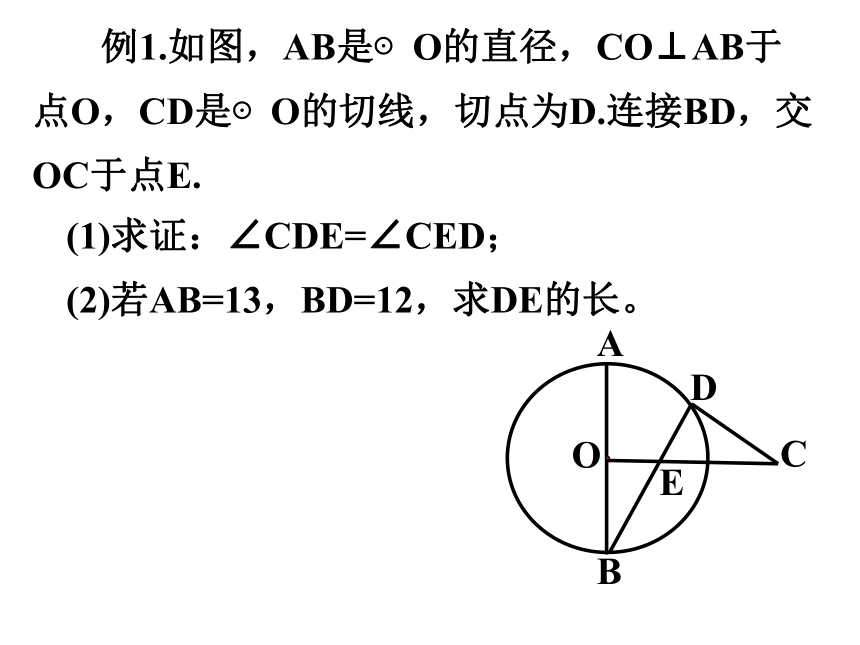
例1.如图,AB是⊙O的直径,CO⊥AB于点O,CD是⊙O的切线,切点为D.连接BD,交OC于点E.
(1)求证:∠CDE=∠CED;
(2)若AB=13,BD=12,求DE的长。
A
B
E
C
O
D
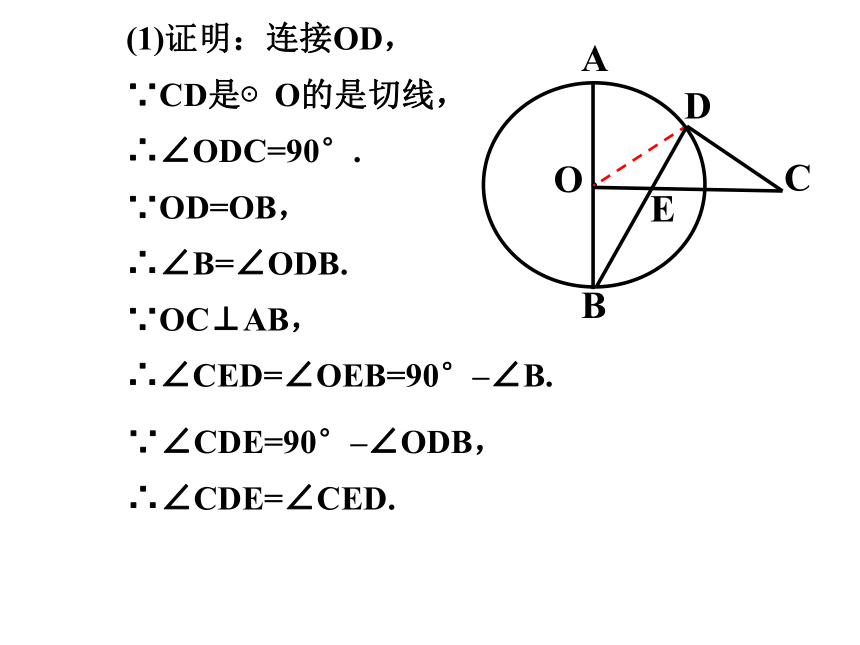
(1)证明:连接OD,
∵CD是⊙O的是切线,
∴∠ODC=90°.
∵OD=OB,
∴∠B=∠ODB.
∵OC⊥AB,
∴∠CED=∠OEB=90°–∠B.
∵∠CDE=90°–∠ODB,
∴∠CDE=∠CED.
A
B
E
C
O
D
(2)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°.
∵AB=13,
∵∠ADB=∠BOE=90°,∠B=∠B,
∴△ABD∽△EBO.
∴AB:EB=DB:BO,
13:EB=12:6.5.
∴
∴EB=
∴DE=BD–EB=12–
∴OB=6.5
A
B
E
C
O
D
169
24
169
24
=
119
24
例2.已知,点C 在以AB为直径的半圆上,∠CAB的平分线AD交BC于点D,⊙O 经过A、D 两点,且圆心O在AB上.
(1)求证:BD是⊙O的切线.
,BC =
(2)若
,求⊙O的面积.
AC
AB
=
1
4
5
4
A
B
E
C
O
D
解:(1)连接OD.
∵AB为直径,
∴∠ACB=900,
∵OA=OD,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∴∠ODB=∠ACB=90°,
∴BD是⊙O的切线.
A
B
E
C
O
D
(2)∵
∵BC2=AB2-AC2, ∴15AC2=80.
∴AC= ,
∴AB=4
设⊙O的半径为r,
∵OD∥AC, ∴OB:AB=OD:AC
解得:r=
∴πr2=
=
∴⊙O的面积为
.
AC
AB
= ,
1
4
15
3
16
256
75
π.
π( )2
15
3
16
256
75
π.
16
3
16
3
4
16
3
r
4
16
3
=
-r
16
3
,
A
B
E
C
O
D
∴AB=4AC,
1.已知⊙O的半径是 5,点A 到圆心O的距离是7 ,则点 A与⊙O的位置关系是 ( ).
A.点 A在⊙O上 B.点A 在⊙O内
C.点A 在⊙O外 D.点 A与圆心O重合
2.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为 ( ).
A.相离 B.相切
C.相交 D.无法确定
练习巩固
C
C
3.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,以点C为圆心,r为半径作圆,若
⊙C与AB的相切,则r的值为( ):
A. r=4cm; B. r=4.8cm
C. r=6cm. D. r=8cm
B
4.如图,△ ABC中,AB=6,BC=10,AC=8,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( ).
相离 B.相切
C.相交 D.不确定
A
B
C
F
G
AF =
GF=
DE =
D
E
C
5.如图,在矩形ABCD中,AB=6,AD=8,
点O在对角线BD上,以OB为半径作⊙O,交BC于
点E,连接DE,若DE是的切线,此时⊙O的半径
为( ).
B.
A. 2 B. C. D.
5
2
35
16
21
10
O
A
B
C
D
E
C
6.如图, ⊙O为△ABC的内切圆,切点分别为D,E,F,P是弧FDE上的一点,若∠A+ ∠C=110度,则∠FPE=_____度
C
O
D
E
A
B
.
F
P
55
7.以O为圆心 的两个同心圆中,大圆的弦AB与小圆相切于点C.若大圆的半径为13cm,小圆的半径为5cm,则弦AB的长为 ,
圆环的面积为 .
O
A
B
C
AC =
24cm
144πcm2
8.如图,已知⊙O 是△ ABC的内切圆,∠A=54°,则∠BOC的度数为 .
O
A
B
C
117°
∠BOC=
90°+ ∠A
2
1
9.如图 ,PA,PB 是⊙O 的切线, ∠P=102°,
则∠DAP+∠C的度数为 .
O
A
B
P
D
C
219°
10.如图,已知⊙P 的半径为2,圆心P在抛物线y= x2-1上运动.当P与x轴相切时,圆心P的坐标为 .
x
y
O
P
P
P
( - , 2)
或( , 2)
y= x2-1
6
6
2
1
2
1
2= x2-1
2
1
4=x2-2
x2=6
x=±
6
11.AB 是⊙O 的弦,C 是⊙O 外一点,BC 是⊙O 的切线,AB 交过 C 点的直径于点 D,OA⊥CD,试判断△BCD 的形状,并说明你的理由.
A
C
O
B
D
∵BC 是⊙O 的切线,
解:△BCD是等腰三角形.
理由如下:
∴OB⊥BC,
∵OA⊥CD,
∴∠AOD=90°,
1
2
3
4
∴∠1+∠2=90°.
∴∠A+∠3=90°.
∵OA=OB,
∴∠A=∠1.
∴∠2=∠3.
∵∠3=∠4.
∴∠2=∠4.
△BCD是等腰三角形.
12.如图,已知P是⊙O 外一点,PO交⊙O 于点C ,OC=CP=2.AB⊥OC,劣弧AB的度数为120°.连接PB.
(1)求BC的长;
(2)求证:PB是⊙O 的切线.
(1)连结OB,
∵弦AB⊥OC,
∴AC=BC= AB,
∵劣弧AB为120°,
∴∠COB=60°.
又∵OC=OB,
∴△OBC是等边三角形,
∴BC=OC=2.
12.如图,已知P是⊙O 外一点,PO交⊙O 于点C ,OC=CP=2.AB⊥OC,劣弧AB的度数为120°.连接PB.
(1)求BC的长;
(2)证明:∵BC=CP=OC=2,
∴BC= OP.
∴△OBP是直角三角形,
∴∠OBP=90°,
∴OB⊥BP.
∵点B在⊙O上,
∴PB是⊙O的切线.
12.如图,已知P是⊙O 外一点,PO交⊙O 于点C ,OC=CP=2.AB⊥OC,劣弧AB的度数为120°.连接PB.
(2)求证:PB是⊙O 的切线.
2
1
13.如图,已知⊙O 是以 BC为直径的△ABC 的外接圆,PO∥AC ,且与BC 的垂线交于点P , OP交AB 于点 D, BC、PA 的延长线交于点E .
(1)求证: PA是⊙O 的切线;
(2)若sinE= ,PA=6 ,求AC 的长.
3
5
A
P
B
E
C
O
D
A
P
B
E
C
O
D
(1)证明:连接OA.
∵AC∥OP,
∴PA是⊙O的切线.
∠2=∠3,
∵OA=OC,
∴∠3=∠4.
∴∠1=∠2.
∵OA=OB,
OP=OP,
∴ ΔAOP≌ΔBOP,
∴∠OAP=∠OBP.
∴∠OAP=∠OBP=90°,
∵OB⊥PB,
∴PA⊥OA,
∴∠1=∠4,
3
4
1
2
3
5
A
P
B
E
C
O
D
∵PB⊥BC,
∴PB是⊙O的切线.
∵PA是⊙O的切线,
∴PA=PB=6.
∵sinE= ,
sinE= ,
PB
PE
∴ = .
6
PE
3
5
∴PE=10.
∴AE=PE-PA=4.
3
5
∵sinE= ,
sinE= ,
OA
OE
∴ = .
OA
OE
3
5
设OA=3x,
∴OE=5x.
∴(5x)2=42+ (3x)2.
∴OA=OB=3.
∴x=1,
∵OP2=OA2+ AP2,
∴OP= .
∵AC∥OP,
∴AC:OP=AE:PE,
∴AC= .
5
3
5
5
6
第24章 圆 期末复习(3)
沪科版
圆与直线的位置关系
如果圆的半径是r,点到圆心的距离为d,那么:
(1)点在圆外 d r;
(2)点在圆上 d r;
(3)点在圆内 d r。
1.点和圆的位置关系:
点和圆的位置关系有: 、 和
.
点在圆外
点在圆内
点在圆上
>
=
<
复习要点
如果圆的半径是r,圆心到直线的距离为d,那么:
(1)直线与圆相离 d r;
(2)直线与圆相切 d r;
(3)直线与圆相交 d r.
2.直线和圆的位置关系:
直线和圆的位置关系有: 、 和 .
相离
相交
相切
>
=
<
直线和圆只有 公共点时,这条直线叫做圆的切线;这个唯一的公共点叫做 .
5.圆的切线的性质
圆的切线垂直于过切点的 ;
6.圆的切线的判定
经过直径的 ,并且 这条的直线是圆的切线.
4.圆的切线的定义
一个
切点
半径
外端
垂直于
7.切线长
经过圆外一点作圆的切线,这点和 之间的线段的长,叫做这点到圆的切线长。从圆外一点可以作出 条圆的切线,它们的切线长 ;这点与圆心的连线 两切线的夹角.
8.三角形内切圆
和三角形各边都 的圆叫做三角形的内切圆,内切圆的圆心是三角形三条 的交点,它到三边的距离相等,叫做三角形的 心.
切点
两
相等
平分
相切
角平分线
内
例1.如图,AB是⊙O的直径,CO⊥AB于点O,CD是⊙O的切线,切点为D.连接BD,交OC于点E.
(1)求证:∠CDE=∠CED;
(2)若AB=13,BD=12,求DE的长。
A
B
E
C
O
D
(1)证明:连接OD,
∵CD是⊙O的是切线,
∴∠ODC=90°.
∵OD=OB,
∴∠B=∠ODB.
∵OC⊥AB,
∴∠CED=∠OEB=90°–∠B.
∵∠CDE=90°–∠ODB,
∴∠CDE=∠CED.
A
B
E
C
O
D
(2)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°.
∵AB=13,
∵∠ADB=∠BOE=90°,∠B=∠B,
∴△ABD∽△EBO.
∴AB:EB=DB:BO,
13:EB=12:6.5.
∴
∴EB=
∴DE=BD–EB=12–
∴OB=6.5
A
B
E
C
O
D
169
24
169
24
=
119
24
例2.已知,点C 在以AB为直径的半圆上,∠CAB的平分线AD交BC于点D,⊙O 经过A、D 两点,且圆心O在AB上.
(1)求证:BD是⊙O的切线.
,BC =
(2)若
,求⊙O的面积.
AC
AB
=
1
4
5
4
A
B
E
C
O
D
解:(1)连接OD.
∵AB为直径,
∴∠ACB=900,
∵OA=OD,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∴∠ODB=∠ACB=90°,
∴BD是⊙O的切线.
A
B
E
C
O
D
(2)∵
∵BC2=AB2-AC2, ∴15AC2=80.
∴AC= ,
∴AB=4
设⊙O的半径为r,
∵OD∥AC, ∴OB:AB=OD:AC
解得:r=
∴πr2=
=
∴⊙O的面积为
.
AC
AB
= ,
1
4
15
3
16
256
75
π.
π( )2
15
3
16
256
75
π.
16
3
16
3
4
16
3
r
4
16
3
=
-r
16
3
,
A
B
E
C
O
D
∴AB=4AC,
1.已知⊙O的半径是 5,点A 到圆心O的距离是7 ,则点 A与⊙O的位置关系是 ( ).
A.点 A在⊙O上 B.点A 在⊙O内
C.点A 在⊙O外 D.点 A与圆心O重合
2.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为 ( ).
A.相离 B.相切
C.相交 D.无法确定
练习巩固
C
C
3.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,以点C为圆心,r为半径作圆,若
⊙C与AB的相切,则r的值为( ):
A. r=4cm; B. r=4.8cm
C. r=6cm. D. r=8cm
B
4.如图,△ ABC中,AB=6,BC=10,AC=8,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( ).
相离 B.相切
C.相交 D.不确定
A
B
C
F
G
AF =
GF=
DE =
D
E
C
5.如图,在矩形ABCD中,AB=6,AD=8,
点O在对角线BD上,以OB为半径作⊙O,交BC于
点E,连接DE,若DE是的切线,此时⊙O的半径
为( ).
B.
A. 2 B. C. D.
5
2
35
16
21
10
O
A
B
C
D
E
C
6.如图, ⊙O为△ABC的内切圆,切点分别为D,E,F,P是弧FDE上的一点,若∠A+ ∠C=110度,则∠FPE=_____度
C
O
D
E
A
B
.
F
P
55
7.以O为圆心 的两个同心圆中,大圆的弦AB与小圆相切于点C.若大圆的半径为13cm,小圆的半径为5cm,则弦AB的长为 ,
圆环的面积为 .
O
A
B
C
AC =
24cm
144πcm2
8.如图,已知⊙O 是△ ABC的内切圆,∠A=54°,则∠BOC的度数为 .
O
A
B
C
117°
∠BOC=
90°+ ∠A
2
1
9.如图 ,PA,PB 是⊙O 的切线, ∠P=102°,
则∠DAP+∠C的度数为 .
O
A
B
P
D
C
219°
10.如图,已知⊙P 的半径为2,圆心P在抛物线y= x2-1上运动.当P与x轴相切时,圆心P的坐标为 .
x
y
O
P
P
P
( - , 2)
或( , 2)
y= x2-1
6
6
2
1
2
1
2= x2-1
2
1
4=x2-2
x2=6
x=±
6
11.AB 是⊙O 的弦,C 是⊙O 外一点,BC 是⊙O 的切线,AB 交过 C 点的直径于点 D,OA⊥CD,试判断△BCD 的形状,并说明你的理由.
A
C
O
B
D
∵BC 是⊙O 的切线,
解:△BCD是等腰三角形.
理由如下:
∴OB⊥BC,
∵OA⊥CD,
∴∠AOD=90°,
1
2
3
4
∴∠1+∠2=90°.
∴∠A+∠3=90°.
∵OA=OB,
∴∠A=∠1.
∴∠2=∠3.
∵∠3=∠4.
∴∠2=∠4.
△BCD是等腰三角形.
12.如图,已知P是⊙O 外一点,PO交⊙O 于点C ,OC=CP=2.AB⊥OC,劣弧AB的度数为120°.连接PB.
(1)求BC的长;
(2)求证:PB是⊙O 的切线.
(1)连结OB,
∵弦AB⊥OC,
∴AC=BC= AB,
∵劣弧AB为120°,
∴∠COB=60°.
又∵OC=OB,
∴△OBC是等边三角形,
∴BC=OC=2.
12.如图,已知P是⊙O 外一点,PO交⊙O 于点C ,OC=CP=2.AB⊥OC,劣弧AB的度数为120°.连接PB.
(1)求BC的长;
(2)证明:∵BC=CP=OC=2,
∴BC= OP.
∴△OBP是直角三角形,
∴∠OBP=90°,
∴OB⊥BP.
∵点B在⊙O上,
∴PB是⊙O的切线.
12.如图,已知P是⊙O 外一点,PO交⊙O 于点C ,OC=CP=2.AB⊥OC,劣弧AB的度数为120°.连接PB.
(2)求证:PB是⊙O 的切线.
2
1
13.如图,已知⊙O 是以 BC为直径的△ABC 的外接圆,PO∥AC ,且与BC 的垂线交于点P , OP交AB 于点 D, BC、PA 的延长线交于点E .
(1)求证: PA是⊙O 的切线;
(2)若sinE= ,PA=6 ,求AC 的长.
3
5
A
P
B
E
C
O
D
A
P
B
E
C
O
D
(1)证明:连接OA.
∵AC∥OP,
∴PA是⊙O的切线.
∠2=∠3,
∵OA=OC,
∴∠3=∠4.
∴∠1=∠2.
∵OA=OB,
OP=OP,
∴ ΔAOP≌ΔBOP,
∴∠OAP=∠OBP.
∴∠OAP=∠OBP=90°,
∵OB⊥PB,
∴PA⊥OA,
∴∠1=∠4,
3
4
1
2
3
5
A
P
B
E
C
O
D
∵PB⊥BC,
∴PB是⊙O的切线.
∵PA是⊙O的切线,
∴PA=PB=6.
∵sinE= ,
sinE= ,
PB
PE
∴ = .
6
PE
3
5
∴PE=10.
∴AE=PE-PA=4.
3
5
∵sinE= ,
sinE= ,
OA
OE
∴ = .
OA
OE
3
5
设OA=3x,
∴OE=5x.
∴(5x)2=42+ (3x)2.
∴OA=OB=3.
∴x=1,
∵OP2=OA2+ AP2,
∴OP= .
∵AC∥OP,
∴AC:OP=AE:PE,
∴AC= .
5
3
5
5
6
