第24章 圆期末复习(3)与圆有关的计算课件(共24张PPT)
文档属性
| 名称 | 第24章 圆期末复习(3)与圆有关的计算课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 698.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 14:11:51 | ||
图片预览






文档简介
(共24张PPT)
第24章 圆 期末复习(3)
沪科版
与圆有关的计算
1.正多边形的有关概念.
A
B
C
E
D
F
O
(
半径R
中心角
边心距r
(3)正多边形的半径
(1)正多边形的中心
(2)正多边形的中心角
(4)正多边形的边心距
正多边形的外接圆和内切圆的公共圆心.
正多边形外接圆的半径
正多边形内切圆的半径.
正多边形的每一条边所对的圆心角.
复习要点
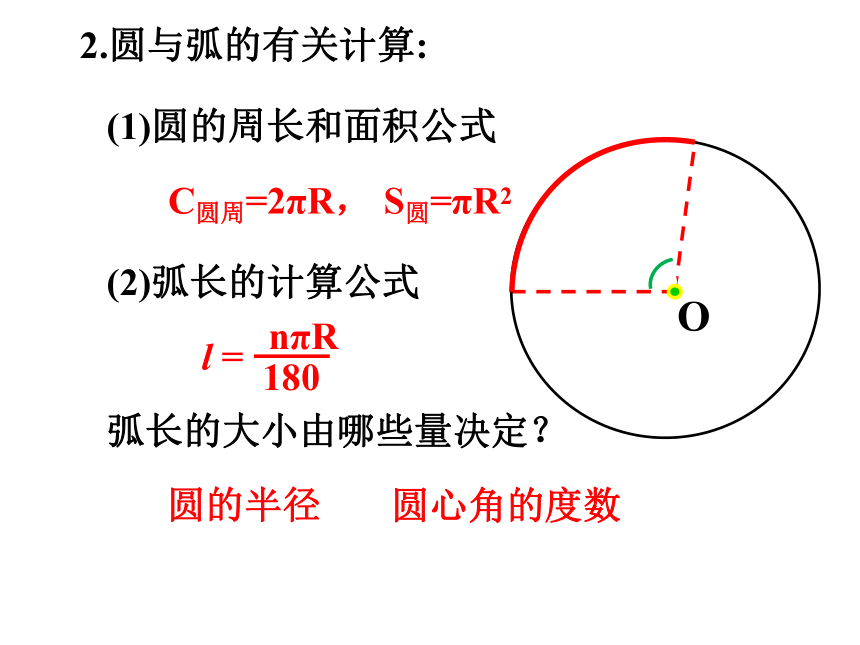
(1)圆的周长和面积公式
(2)弧长的计算公式
2.圆与弧的有关计算:
C圆周=2πR,
S圆=πR2
l =
nπR
180
O
弧长的大小由哪些量决定?
圆的半径
圆心角的度数
A
B
O
S扇形=
=
1
2
×
×R
=
1
2
C1R
n°
nπR
180
nπR2
360
扇形面积公式
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
3.扇形与扇形面积公式
4.圆柱的展开图:
D
B
C
A
r
h
S侧 =2πr h
S全=2πr h+2 π r2
圆柱的侧面展开图是矩形,矩形的两边长
分别是圆柱的母线长和底面圆的周长.
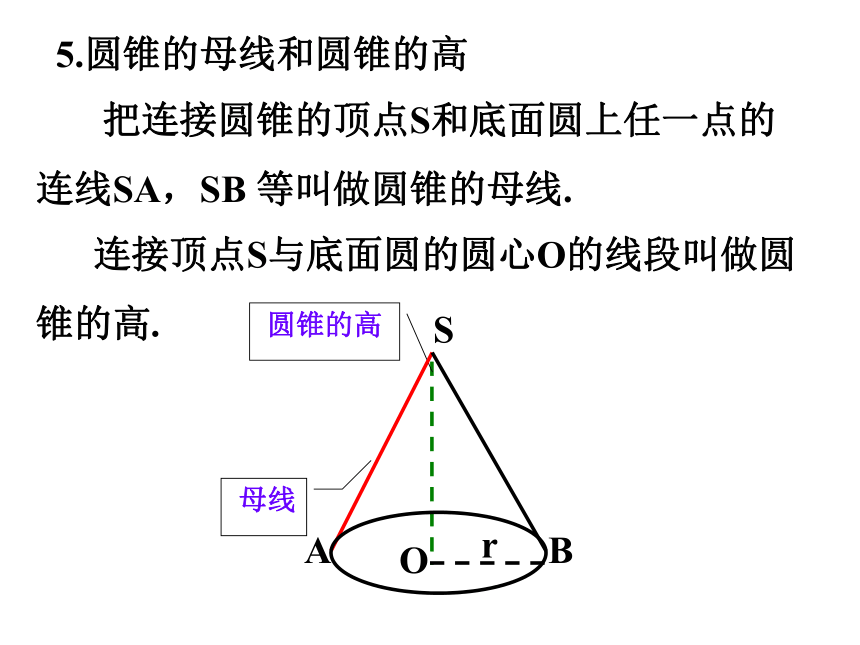
圆锥的高
母线
S
A
O
B
r
把连接圆锥的顶点S和底面圆上任一点的连线SA,SB 等叫做圆锥的母线.
连接顶点S与底面圆的圆心O的线段叫做圆锥的高.
5.圆锥的母线和圆锥的高
h
r
由勾股定理得:
r2+h2= 2
如果用r表示圆锥底面的半径, h表示圆锥的高线长, l表示圆锥的母线长,那么r,h, l之间有怎样的数量关系呢?
O
S
A
6.圆锥的母线长
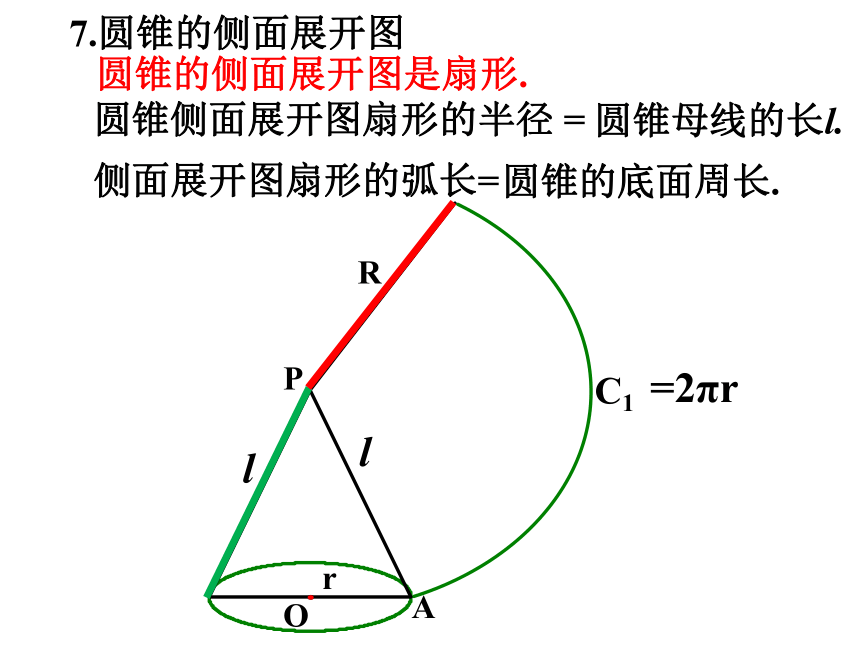
7.圆锥的侧面展开图
O
A
P
r
l
圆锥侧面展开图扇形的半径 =
侧面展开图扇形的弧长=
C1
圆锥母线的长l.
R
l
圆锥的底面周长.
=2πr
圆锥的侧面展开图是扇形.
8.圆锥的侧面积
O
A
S
r
l
C1
∴ S 侧 = πrl
(r表示圆锥底面的半径, l表示圆锥的母线长 )
∴
∵
S扇形=
C1l,
1
2
R
S侧=
C1l,
1
2
C1
=2πr,
S侧=
l,
1
2
2πr
9.圆锥的全面积
O
A
S
r
l
圆锥的侧面积与底面积的和叫做圆锥的全面积.
=πr(r+l)
例1.如下图,所示的三角形铁皮余料,剪下扇形制成圆锥形玩具,已知∠C=90°,AC=BC=4cm,使剪下的扇形边缘半径在三角形边上,弧与其他边相切,设计裁剪的方案图,直接写出扇形的半径长.
O
AB=
2
4
R1=
2
2
R2=
4
R3=
2
R4=
2
4
-4
例题解析
例2.如图,圆锥的底面半径为2cm,母线长为8cm,一只蚂蚁从底面圆周上一点A出发,沿圆锥侧面爬行一周回到A点,求蚂蚁爬行的最短路线长是多少?
B
A
O
A′
解:
nπR
180
=2π r,
R=8,
r=2,
∴n=90.
∴∠AOA′=90°.
在Rt△ABC中,
∵AA′2=AO2+OA′2
∴AA′2=82+82
∴AA′=8
2
∵
∴蚂蚁爬行的最短路线长是
8
2
cm.
1.如图,在正六边形ABCDEF中,AC= ,
那么它的边长是( ).
A. 1 B.
C. D. 2
A
B
C
D
E
F
3
2
3
2
D
练习巩固
2.一条弧所对的圆心角是135°,弧长等于半径
为5 cm的圆的周长的3倍,则这条弧所在的圆
的半径是( ).
A.40 cm B.30 cm C.20 cm D.15 cm
A
3.扇形的半径为3,且圆心角为60°,则此扇形的弧长是( ) .
A. B. C. D.
1
2
π
π
3
2
π
2π
B
4.一个圆锥的侧面积是底面积的2倍,则这个圆锥的侧面展开图的扇形的圆心角是( ).
A. 30° B. 60° C. 90° D. 180°
D
5.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为 ( ).
A.9 B. 18 C. 36 D.72
5
5
5
5
B
6.一个扇形所在圆的半径为3cm,扇形的圆心角为120°,则扇形的面积是 cm2. (结果保留π)
7. 120°的圆心角所对的弧长是12πcm,
则此弧所在的圆的半径是 cm.
3π
18
8.如图,AC⊥BC,AC=BC=4.以AC为直径作半圆,圆心为点O,以点C为圆心,BC为半径作AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 .
︵
A
B
E
O
C
D
3
5π
-2
3
9.若一个正多边形的一个外角等于18°,则这个正多边形的边数是 .
10.如图,点B、C把AD分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=1,则图中阴影部分的面积是 .
︵
20
8
π
11.如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 .
A
B
C
D
8+8
2
12.如图,圆锥侧面展开得到扇形,此扇形半径CA=6,圆心角∠ACB=120°, 则此圆锥高 OC 的长度是 .
4
2
13.如图,已知半径为 1的⊙O上有三点
A、B、C,OC与AB交于点D, ∠ADO=85°, ∠CAB=20°,则阴影部分的扇形面积OAC是
.
O
A
B
C
D
36
5π
14.如图,已知⊙O是正六边形ABCDEF的外接圆,AB的长为 ,
2
3
则阴影部分的
面积是 .
π
O
A
B
C
D
E
F
︵
3
2π
-
3
15.如图,正六边形ABCDEF的周长为 24cm,连接这个六边形的各边中点G,H,K,
L,M,N,则六边形GHKLMN的周长是 cm.
F
A
B
C
D
E
K
N
H
G
L
M
3
12
16.如图,四边形ABCD是⊙O的内接正四边形,分别以点A,O为圆心,取大于 OA的定长为半径
画弧,两弧相交于点M,N,作直线MN. MB 交
⊙O于点E,F,若OA=1,则BE,AE,AB所围成
的阴影面积为 .
A
B
C
O
D
M
N
E
F
1
2
︵
12
π
-
2
1
3
4
+
第24章 圆 期末复习(3)
沪科版
与圆有关的计算
1.正多边形的有关概念.
A
B
C
E
D
F
O
(
半径R
中心角
边心距r
(3)正多边形的半径
(1)正多边形的中心
(2)正多边形的中心角
(4)正多边形的边心距
正多边形的外接圆和内切圆的公共圆心.
正多边形外接圆的半径
正多边形内切圆的半径.
正多边形的每一条边所对的圆心角.
复习要点
(1)圆的周长和面积公式
(2)弧长的计算公式
2.圆与弧的有关计算:
C圆周=2πR,
S圆=πR2
l =
nπR
180
O
弧长的大小由哪些量决定?
圆的半径
圆心角的度数
A
B
O
S扇形=
=
1
2
×
×R
=
1
2
C1R
n°
nπR
180
nπR2
360
扇形面积公式
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
3.扇形与扇形面积公式
4.圆柱的展开图:
D
B
C
A
r
h
S侧 =2πr h
S全=2πr h+2 π r2
圆柱的侧面展开图是矩形,矩形的两边长
分别是圆柱的母线长和底面圆的周长.
圆锥的高
母线
S
A
O
B
r
把连接圆锥的顶点S和底面圆上任一点的连线SA,SB 等叫做圆锥的母线.
连接顶点S与底面圆的圆心O的线段叫做圆锥的高.
5.圆锥的母线和圆锥的高
h
r
由勾股定理得:
r2+h2= 2
如果用r表示圆锥底面的半径, h表示圆锥的高线长, l表示圆锥的母线长,那么r,h, l之间有怎样的数量关系呢?
O
S
A
6.圆锥的母线长
7.圆锥的侧面展开图
O
A
P
r
l
圆锥侧面展开图扇形的半径 =
侧面展开图扇形的弧长=
C1
圆锥母线的长l.
R
l
圆锥的底面周长.
=2πr
圆锥的侧面展开图是扇形.
8.圆锥的侧面积
O
A
S
r
l
C1
∴ S 侧 = πrl
(r表示圆锥底面的半径, l表示圆锥的母线长 )
∴
∵
S扇形=
C1l,
1
2
R
S侧=
C1l,
1
2
C1
=2πr,
S侧=
l,
1
2
2πr
9.圆锥的全面积
O
A
S
r
l
圆锥的侧面积与底面积的和叫做圆锥的全面积.
=πr(r+l)
例1.如下图,所示的三角形铁皮余料,剪下扇形制成圆锥形玩具,已知∠C=90°,AC=BC=4cm,使剪下的扇形边缘半径在三角形边上,弧与其他边相切,设计裁剪的方案图,直接写出扇形的半径长.
O
AB=
2
4
R1=
2
2
R2=
4
R3=
2
R4=
2
4
-4
例题解析
例2.如图,圆锥的底面半径为2cm,母线长为8cm,一只蚂蚁从底面圆周上一点A出发,沿圆锥侧面爬行一周回到A点,求蚂蚁爬行的最短路线长是多少?
B
A
O
A′
解:
nπR
180
=2π r,
R=8,
r=2,
∴n=90.
∴∠AOA′=90°.
在Rt△ABC中,
∵AA′2=AO2+OA′2
∴AA′2=82+82
∴AA′=8
2
∵
∴蚂蚁爬行的最短路线长是
8
2
cm.
1.如图,在正六边形ABCDEF中,AC= ,
那么它的边长是( ).
A. 1 B.
C. D. 2
A
B
C
D
E
F
3
2
3
2
D
练习巩固
2.一条弧所对的圆心角是135°,弧长等于半径
为5 cm的圆的周长的3倍,则这条弧所在的圆
的半径是( ).
A.40 cm B.30 cm C.20 cm D.15 cm
A
3.扇形的半径为3,且圆心角为60°,则此扇形的弧长是( ) .
A. B. C. D.
1
2
π
π
3
2
π
2π
B
4.一个圆锥的侧面积是底面积的2倍,则这个圆锥的侧面展开图的扇形的圆心角是( ).
A. 30° B. 60° C. 90° D. 180°
D
5.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心,ED为半径作半圆,交A、B所在的直线于M、N两点,分别以直径MD、ND为直径作半圆,则阴影部分面积为 ( ).
A.9 B. 18 C. 36 D.72
5
5
5
5
B
6.一个扇形所在圆的半径为3cm,扇形的圆心角为120°,则扇形的面积是 cm2. (结果保留π)
7. 120°的圆心角所对的弧长是12πcm,
则此弧所在的圆的半径是 cm.
3π
18
8.如图,AC⊥BC,AC=BC=4.以AC为直径作半圆,圆心为点O,以点C为圆心,BC为半径作AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 .
︵
A
B
E
O
C
D
3
5π
-2
3
9.若一个正多边形的一个外角等于18°,则这个正多边形的边数是 .
10.如图,点B、C把AD分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=1,则图中阴影部分的面积是 .
︵
20
8
π
11.如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是 .
A
B
C
D
8+8
2
12.如图,圆锥侧面展开得到扇形,此扇形半径CA=6,圆心角∠ACB=120°, 则此圆锥高 OC 的长度是 .
4
2
13.如图,已知半径为 1的⊙O上有三点
A、B、C,OC与AB交于点D, ∠ADO=85°, ∠CAB=20°,则阴影部分的扇形面积OAC是
.
O
A
B
C
D
36
5π
14.如图,已知⊙O是正六边形ABCDEF的外接圆,AB的长为 ,
2
3
则阴影部分的
面积是 .
π
O
A
B
C
D
E
F
︵
3
2π
-
3
15.如图,正六边形ABCDEF的周长为 24cm,连接这个六边形的各边中点G,H,K,
L,M,N,则六边形GHKLMN的周长是 cm.
F
A
B
C
D
E
K
N
H
G
L
M
3
12
16.如图,四边形ABCD是⊙O的内接正四边形,分别以点A,O为圆心,取大于 OA的定长为半径
画弧,两弧相交于点M,N,作直线MN. MB 交
⊙O于点E,F,若OA=1,则BE,AE,AB所围成
的阴影面积为 .
A
B
C
O
D
M
N
E
F
1
2
︵
12
π
-
2
1
3
4
+
