第26章概率初步期末复习 课件(共30张PPT)
文档属性
| 名称 | 第26章概率初步期末复习 课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 08:06:02 | ||
图片预览










文档简介
(共30张PPT)
第26章 概率初步 期末复习
沪科版
①必然事件:在一定的条件下, 会发生的事件.
(2)相关定义
②不可能事件:在一定的条件下,必然 发生的事件.
③确定事件: 事件和 事件统称确定事件.
④随机事件:在一定条件下,可能 也可能不发生
的事件.
必定
(1)事件按可能性分类:
1.事件发生的可能性
事件
不
必然
不可能
发生
确定事件
随机事件
必然事件
不可能事件
复习要点
2.概率的定义
(1)定义:表示一个事件发生的 大小
的这个数叫做概率,通常用字母P表示.
(2)P(必然事件)= ;
P(不可能事件)= ;
P(随机事件)满足 .
可能性
1
0
0<P <1
②复杂情况下的概率用列举法求,包括 法和 法.
③利用频率估计概率:通过反复试验,用平稳时的 估计随机事件的概率.
列表
画树状图
频率
3.概率的求法
①较简单问题情境下的概率:在一次实验中,有n种可能的结果,事件A包含其中的m种结果,则P(A)= .
m
n
5.游戏的公平与否
游戏双方获胜的概率 的游戏是公平的,否则是不公平的
相等
4.用树状(形)图或列表法求等可能事件的概率
1.画树状(形)图是列举随机事件的所有可能结果的重要方法,通过树状(形)图,把所有可能的结果一一列出,有利于帮助我们分析问题,并且可以避免出现重复和遗漏,既形象直观又条理分明.
2.列表法也是列举随机事件的所有可能结果的一个重要的方法,列表法是画“树状(形)图”的必要补充.
例题解析
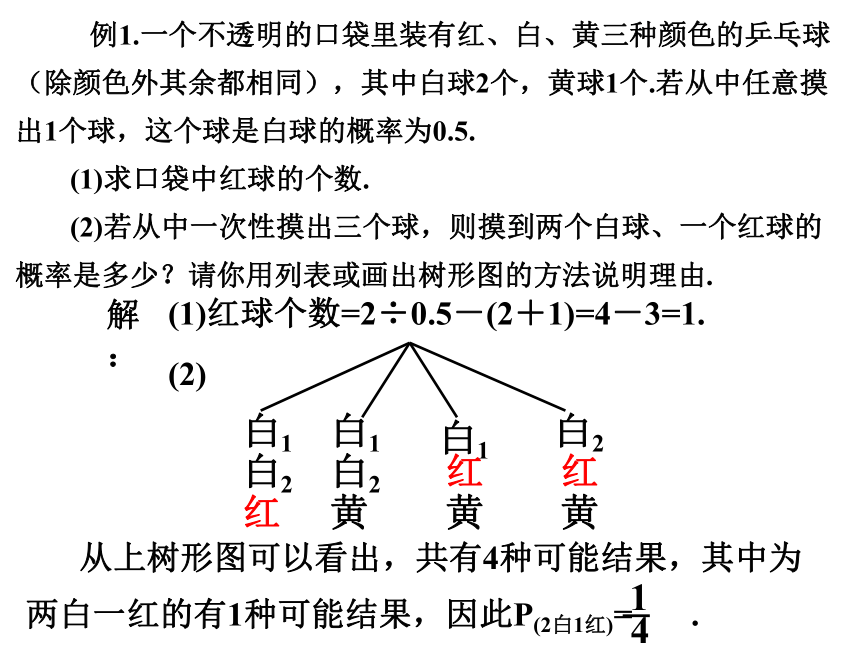
例1.一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中白球2个,黄球1个.若从中任意摸出1个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)若从中一次性摸出三个球,则摸到两个白球、一个红球的概率是多少?请你用列表或画出树形图的方法说明理由.
解:
(1)红球个数=2÷0.5-(2+1)=4-3=1.
白1
白1
白1
白2
白2
白2
红
红
红
黄
黄
黄
从上树形图可以看出,共有4种可能结果,其中为
两白一红的有1种可能结果,因此P(2白1红)= .
(2)
例1.一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中白球2个,黄球1个.若从中任意摸出1个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)若从中一次性摸出三个球,则摸到两个白球、一个红球的概率是多少?请你用列表或画出树形图的方法说明理由.
1
4
例2.在数学课上,老师拿出4张牌,牌面分别是1、2、3和4. 老师提出以下两个问题:
(1)若随机抽取两张牌,则抽出牌面数字刚好
是方程x2-4x+3=0的两个根的概率是多少?
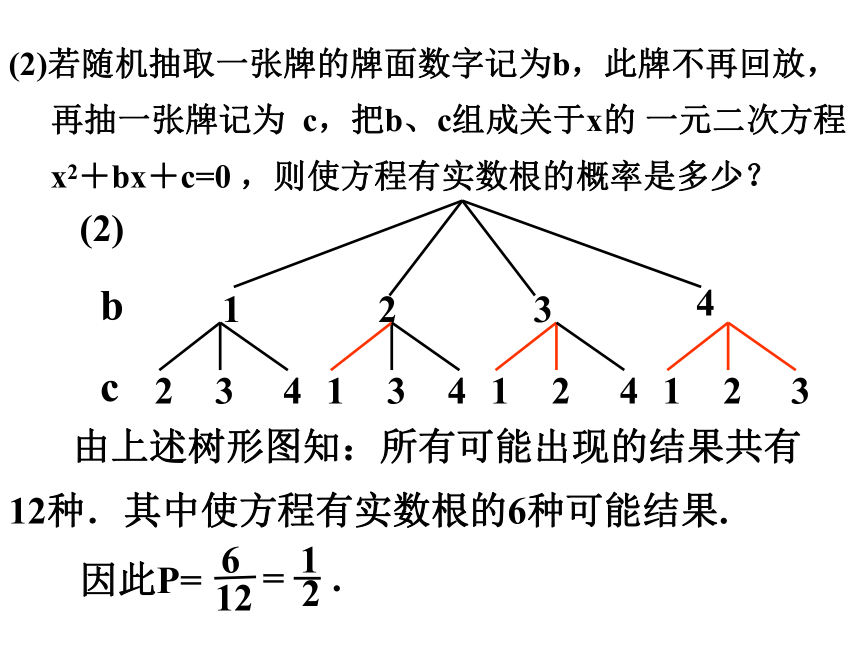
(2)若随机抽取一张牌的牌面数字记为b,此牌不再
回放,再抽一张牌记为 c,把b、c组成关于x的
一元二次方程:x2+bx+c=0 ,则使方程有实
数根的概率是多少?
解:(1)
若随机抽取两张牌,则抽出牌面数字的所有可能结果有(1,2)、(1,3)、(1,4)、(2,3)、(2,4)、(3,4)这6种,
因此P(方程两根)=
而满足是方程 x2-4x+3=0的根的只有(1,3)1种.
1
6
(1)若随机抽取两张牌,则抽出牌面数字刚好
是方程x2-4x+3=0的两个根的概率是多少?
例2.在数学课上,老师拿出4张牌,牌面分别是1、2、3和4. 老师提出以下两个问题:
(2)
1
2
3
4
b
3
2
4
3
1
4
2
1
4
2
1
3
c
由上述树形图知:所有可能出现的结果共有12种.其中使方程有实数根的6种可能结果.
(2)若随机抽取一张牌的牌面数字记为b,此牌不再回放,
再抽一张牌记为 c,把b、c组成关于x的 一元二次方程
x2+bx+c=0 ,则使方程有实数根的概率是多少?
6
12
1
2
= .
因此P=
1.下列事件是必然事件的是( ).
A.随意掷两个质地均匀的骰子,朝上面的
点数之和为 7
B.抛一枚硬币,正面朝下
C.5 个人分成4组,一定有 2 个人分在一组
D.打开电视,正在播放电视连续剧《西游记》
练习巩固
C
2.下列事件中,属于随机事件的有( ).
① 太阳从东边升起;
② 任意摸一张福利彩票会中奖;
③ 随意掷一枚骰子,朝上面的点数为 3;
④ 小聪长大后成为一名警察
A.①②③ B.①③④
C.②③④ D.①②④
C
3.在一次游戏中,小明连掷两枚骰子,骰子点数的和是7的概率是( ) .
A. B. C. D.
1
2
1
36
1
6
1
12
4.把分别写有1,2,3的三张卡片排成三位数,其中是奇数的概率是( ).
A. B. C. D.
1
6
1
3
1
2
2
3
C
D
5.一个布袋中有4个除颜色外其余都相同的小球,其中3个白球,1个红球.从袋中任意摸出1个球是白球的概率是( ).
A. B. C. D.
3
4
1
4
2
3
1
3
6.小李是9人队伍中的一员,他们随机排成一列队伍, 从1开始按顺序报数,小李报到偶数的概率是( ).
A. B. C. D.
2
3
4
9
1
2
1
9
A
B
7.从一幅扑克牌中取出的两组牌,分别是黑桃1,2,3,4红桃1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌面数字之和等于7的概率是( ).
A. B. C. D.
1
4
1
8
1
16
1
32
B
8. 在一个不透明的袋子中,装有红球、黄球、蓝球、白球各1个,这些球除颜色外无其他差别,从袋中随机取出一个球,取出红球的概率为( ).
A. B. C. D.
1
2
1
3
1
4
1
C
9.三张背面完全相同的数字牌,它们的正面分别印有数字“1”、“2”、“3”,将它们背面朝上,洗匀后随机抽取一张,记录牌上的数字并把牌放回,再重复这样的步骤两次,得到三个数字a、b、c,则以a、b、c为边长正好构成等边三角形的概率是( ).
A. B. C. D.
1
9
1
27
5
9
1
3
A
10.小燕一家三口在商场参加抽奖活动,每人只有一次抽奖机会:在一个不透明的箱子中装有红、黄、白三种球各 1 个,这些球除颜色外无其他差别,从箱子中随机摸出 1 个球,然后放回箱子中轮到下一个人摸球,三人摸到球的颜色都不相同的概率是( ).
A. B. C. D.
1
27
1
3
1
9
2
9
D
11.在一个不透明的布袋中装有红色、白色玻璃球共 40 个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的概率稳定在 15% 左右,则口袋中红色球可能有( ). A.4个 B.6个 C.34个 D.36个
B
12.一个口袋中有 3 个红球和若干个黄球,在不允许将球倒出来数的前提下,小强为估计其中的黄球数,采用如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,……不断重复上述过程.小强共摸了 100 次,其中 20 次摸到红球.根据上述数据,小明可估计口袋中的黄球大约有( ). A.18个 B.15个 C.12个 D.10个
C
13.把4个完全相同的乒乓球标上数字2,3,4,5,然后放到一个不透明的口袋中,第一次任意摸出一个球(不放回),第二次再任意摸出一个球. (1)请补充完整下面的树形图.
(2)根据树形图可知,两次摸出的球所标数字之和是7的概率是 .
开始
第一次
2
3
5
4
5
9
4
9
第二次
两数之和为
2
6
2
7
5
6
4
4
2
5
7
8
8
3
3
5
5
7
3
7
1
3
14. 某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售.每种型号的打印机均需要一种芯片配套才能打印.
(1)下列是该店用树形图或列表设计的配套方案,
①的位置应填写____,②的位置应填写_____ ;
(2)若仅有B型打印机与E种芯片不配套,则上面
(1)中的方案配套成功率是____.
芯片
打印机 C D E
A (A,C) (A,D) ②
B (B,C) (B,D) (B,E)
配套
方案
A
C
D
E
B
C
D
①
E
(A,E)
5
6
15.如图是一个被等分成 6 个扇形,可自由转动的转盘. 转动转盘,当转盘停止后,指针指向红色区域的概率是_____.
1
2
16.从某玉米种子中抽取 6 批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 100 400 800 1 000 2 000 5 000
发芽种子粒数 85 298 652 793 1 604 4 005
发芽频率 0.850 0.745 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为______(精确到0.1).
0.8
17. 在军事选拔赛中,某部队一名战士射击了160次,其成绩记录如下:
射击次数 20 40 60 80 100 120 140 160
射中9环以上的次数 31 49 63 81 97 110 132
射中9环以上的频率 0.80 0.78 0.82 0.79 0.81 0.81 0.79
(1)补全上表两个空格的数据
(射中9环以上的次数为整数,频率精确到0.01);
(2)根据上表估计该战士射击一次时“射中9环以上”
的概率(精确到0.1),并简述理由.
16
0.83
18.在一个不透明的口袋里装有白、黄、蓝三种颜色的小球(除颜色外其余部分都相同),其中白球有2个,黄球有1个,蓝球有1 个.(1)试求从袋中任意摸出一个是白球的概率;(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树形图或列表法,求两次摸出都是白球的概率.
(1)P=
1
3
(2)
白1
白2
黄
蓝
白2
蓝
黄
黄
白1
蓝
白1
白2
黄
蓝
白1
白2
∴P=
2
12
1
6
=
19.在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸取一个小球然后放回,再随机地摸出一个小球,求两次取的小球的标号和大于或等于5的概率.解答过程要求列表或画出具体的树形图.
由上述树形图知:所有可能出现的结果共有16种.其中数字和大于或等于5共有10种可能结果.
解:
2
1
3
4
1
2
3
4
1
2
3
4
3
1
2
4
1
2
4
3
第一次
第二次
10
16
5
8
= .
因此P=
19.一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y.
(1)用列表法或树状图法,列出点M(x,y)的所有可能结果;
(2)求点M(x,y)在双曲线y=- 上的概率.
2
x
19.一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y.
(1)用列表法或树状图法,列出点M(x,y)的所有可能结果;
(1)用列表法
∴点M的所有可能结果有:
(-1,1),
(-1,2),
(1,-1),
(1,2),
(2,-1),
(2,1)六种.
-1 1 2
-1
1
2
(-1,1)
(-1,2)
(1,-1)
(1,2)
(2,-1)
(2,1)
19.一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y.
(1)用列表法或树状图法,列出点M(x,y)的所有可能结果;
(2)用树状图法
-1
1
2
1
2
-1
2
-1
1
∴点M的所有可能结果有:
(-1,1),
(-1,2),
(1,-1),
(1,2),
(2,-1),
(2,1)六种.
19.一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y.
(2)求点M(x,y)在双曲线y=- 上的概率.
2
x
∴结果有6种可能性,且出现的可能性相等,
其中符合条件的有2种.
∴P=
2
6
1
3
=
∴点M(x,y)在双曲线上的概率为 .
1
3
(2)
第26章 概率初步 期末复习
沪科版
①必然事件:在一定的条件下, 会发生的事件.
(2)相关定义
②不可能事件:在一定的条件下,必然 发生的事件.
③确定事件: 事件和 事件统称确定事件.
④随机事件:在一定条件下,可能 也可能不发生
的事件.
必定
(1)事件按可能性分类:
1.事件发生的可能性
事件
不
必然
不可能
发生
确定事件
随机事件
必然事件
不可能事件
复习要点
2.概率的定义
(1)定义:表示一个事件发生的 大小
的这个数叫做概率,通常用字母P表示.
(2)P(必然事件)= ;
P(不可能事件)= ;
P(随机事件)满足 .
可能性
1
0
0<P <1
②复杂情况下的概率用列举法求,包括 法和 法.
③利用频率估计概率:通过反复试验,用平稳时的 估计随机事件的概率.
列表
画树状图
频率
3.概率的求法
①较简单问题情境下的概率:在一次实验中,有n种可能的结果,事件A包含其中的m种结果,则P(A)= .
m
n
5.游戏的公平与否
游戏双方获胜的概率 的游戏是公平的,否则是不公平的
相等
4.用树状(形)图或列表法求等可能事件的概率
1.画树状(形)图是列举随机事件的所有可能结果的重要方法,通过树状(形)图,把所有可能的结果一一列出,有利于帮助我们分析问题,并且可以避免出现重复和遗漏,既形象直观又条理分明.
2.列表法也是列举随机事件的所有可能结果的一个重要的方法,列表法是画“树状(形)图”的必要补充.
例题解析
例1.一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中白球2个,黄球1个.若从中任意摸出1个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)若从中一次性摸出三个球,则摸到两个白球、一个红球的概率是多少?请你用列表或画出树形图的方法说明理由.
解:
(1)红球个数=2÷0.5-(2+1)=4-3=1.
白1
白1
白1
白2
白2
白2
红
红
红
黄
黄
黄
从上树形图可以看出,共有4种可能结果,其中为
两白一红的有1种可能结果,因此P(2白1红)= .
(2)
例1.一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中白球2个,黄球1个.若从中任意摸出1个球,这个球是白球的概率为0.5.
(1)求口袋中红球的个数.
(2)若从中一次性摸出三个球,则摸到两个白球、一个红球的概率是多少?请你用列表或画出树形图的方法说明理由.
1
4
例2.在数学课上,老师拿出4张牌,牌面分别是1、2、3和4. 老师提出以下两个问题:
(1)若随机抽取两张牌,则抽出牌面数字刚好
是方程x2-4x+3=0的两个根的概率是多少?
(2)若随机抽取一张牌的牌面数字记为b,此牌不再
回放,再抽一张牌记为 c,把b、c组成关于x的
一元二次方程:x2+bx+c=0 ,则使方程有实
数根的概率是多少?
解:(1)
若随机抽取两张牌,则抽出牌面数字的所有可能结果有(1,2)、(1,3)、(1,4)、(2,3)、(2,4)、(3,4)这6种,
因此P(方程两根)=
而满足是方程 x2-4x+3=0的根的只有(1,3)1种.
1
6
(1)若随机抽取两张牌,则抽出牌面数字刚好
是方程x2-4x+3=0的两个根的概率是多少?
例2.在数学课上,老师拿出4张牌,牌面分别是1、2、3和4. 老师提出以下两个问题:
(2)
1
2
3
4
b
3
2
4
3
1
4
2
1
4
2
1
3
c
由上述树形图知:所有可能出现的结果共有12种.其中使方程有实数根的6种可能结果.
(2)若随机抽取一张牌的牌面数字记为b,此牌不再回放,
再抽一张牌记为 c,把b、c组成关于x的 一元二次方程
x2+bx+c=0 ,则使方程有实数根的概率是多少?
6
12
1
2
= .
因此P=
1.下列事件是必然事件的是( ).
A.随意掷两个质地均匀的骰子,朝上面的
点数之和为 7
B.抛一枚硬币,正面朝下
C.5 个人分成4组,一定有 2 个人分在一组
D.打开电视,正在播放电视连续剧《西游记》
练习巩固
C
2.下列事件中,属于随机事件的有( ).
① 太阳从东边升起;
② 任意摸一张福利彩票会中奖;
③ 随意掷一枚骰子,朝上面的点数为 3;
④ 小聪长大后成为一名警察
A.①②③ B.①③④
C.②③④ D.①②④
C
3.在一次游戏中,小明连掷两枚骰子,骰子点数的和是7的概率是( ) .
A. B. C. D.
1
2
1
36
1
6
1
12
4.把分别写有1,2,3的三张卡片排成三位数,其中是奇数的概率是( ).
A. B. C. D.
1
6
1
3
1
2
2
3
C
D
5.一个布袋中有4个除颜色外其余都相同的小球,其中3个白球,1个红球.从袋中任意摸出1个球是白球的概率是( ).
A. B. C. D.
3
4
1
4
2
3
1
3
6.小李是9人队伍中的一员,他们随机排成一列队伍, 从1开始按顺序报数,小李报到偶数的概率是( ).
A. B. C. D.
2
3
4
9
1
2
1
9
A
B
7.从一幅扑克牌中取出的两组牌,分别是黑桃1,2,3,4红桃1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌面数字之和等于7的概率是( ).
A. B. C. D.
1
4
1
8
1
16
1
32
B
8. 在一个不透明的袋子中,装有红球、黄球、蓝球、白球各1个,这些球除颜色外无其他差别,从袋中随机取出一个球,取出红球的概率为( ).
A. B. C. D.
1
2
1
3
1
4
1
C
9.三张背面完全相同的数字牌,它们的正面分别印有数字“1”、“2”、“3”,将它们背面朝上,洗匀后随机抽取一张,记录牌上的数字并把牌放回,再重复这样的步骤两次,得到三个数字a、b、c,则以a、b、c为边长正好构成等边三角形的概率是( ).
A. B. C. D.
1
9
1
27
5
9
1
3
A
10.小燕一家三口在商场参加抽奖活动,每人只有一次抽奖机会:在一个不透明的箱子中装有红、黄、白三种球各 1 个,这些球除颜色外无其他差别,从箱子中随机摸出 1 个球,然后放回箱子中轮到下一个人摸球,三人摸到球的颜色都不相同的概率是( ).
A. B. C. D.
1
27
1
3
1
9
2
9
D
11.在一个不透明的布袋中装有红色、白色玻璃球共 40 个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的概率稳定在 15% 左右,则口袋中红色球可能有( ). A.4个 B.6个 C.34个 D.36个
B
12.一个口袋中有 3 个红球和若干个黄球,在不允许将球倒出来数的前提下,小强为估计其中的黄球数,采用如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,……不断重复上述过程.小强共摸了 100 次,其中 20 次摸到红球.根据上述数据,小明可估计口袋中的黄球大约有( ). A.18个 B.15个 C.12个 D.10个
C
13.把4个完全相同的乒乓球标上数字2,3,4,5,然后放到一个不透明的口袋中,第一次任意摸出一个球(不放回),第二次再任意摸出一个球. (1)请补充完整下面的树形图.
(2)根据树形图可知,两次摸出的球所标数字之和是7的概率是 .
开始
第一次
2
3
5
4
5
9
4
9
第二次
两数之和为
2
6
2
7
5
6
4
4
2
5
7
8
8
3
3
5
5
7
3
7
1
3
14. 某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售.每种型号的打印机均需要一种芯片配套才能打印.
(1)下列是该店用树形图或列表设计的配套方案,
①的位置应填写____,②的位置应填写_____ ;
(2)若仅有B型打印机与E种芯片不配套,则上面
(1)中的方案配套成功率是____.
芯片
打印机 C D E
A (A,C) (A,D) ②
B (B,C) (B,D) (B,E)
配套
方案
A
C
D
E
B
C
D
①
E
(A,E)
5
6
15.如图是一个被等分成 6 个扇形,可自由转动的转盘. 转动转盘,当转盘停止后,指针指向红色区域的概率是_____.
1
2
16.从某玉米种子中抽取 6 批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 100 400 800 1 000 2 000 5 000
发芽种子粒数 85 298 652 793 1 604 4 005
发芽频率 0.850 0.745 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为______(精确到0.1).
0.8
17. 在军事选拔赛中,某部队一名战士射击了160次,其成绩记录如下:
射击次数 20 40 60 80 100 120 140 160
射中9环以上的次数 31 49 63 81 97 110 132
射中9环以上的频率 0.80 0.78 0.82 0.79 0.81 0.81 0.79
(1)补全上表两个空格的数据
(射中9环以上的次数为整数,频率精确到0.01);
(2)根据上表估计该战士射击一次时“射中9环以上”
的概率(精确到0.1),并简述理由.
16
0.83
18.在一个不透明的口袋里装有白、黄、蓝三种颜色的小球(除颜色外其余部分都相同),其中白球有2个,黄球有1个,蓝球有1 个.(1)试求从袋中任意摸出一个是白球的概率;(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树形图或列表法,求两次摸出都是白球的概率.
(1)P=
1
3
(2)
白1
白2
黄
蓝
白2
蓝
黄
黄
白1
蓝
白1
白2
黄
蓝
白1
白2
∴P=
2
12
1
6
=
19.在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机地摸取一个小球然后放回,再随机地摸出一个小球,求两次取的小球的标号和大于或等于5的概率.解答过程要求列表或画出具体的树形图.
由上述树形图知:所有可能出现的结果共有16种.其中数字和大于或等于5共有10种可能结果.
解:
2
1
3
4
1
2
3
4
1
2
3
4
3
1
2
4
1
2
4
3
第一次
第二次
10
16
5
8
= .
因此P=
19.一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y.
(1)用列表法或树状图法,列出点M(x,y)的所有可能结果;
(2)求点M(x,y)在双曲线y=- 上的概率.
2
x
19.一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y.
(1)用列表法或树状图法,列出点M(x,y)的所有可能结果;
(1)用列表法
∴点M的所有可能结果有:
(-1,1),
(-1,2),
(1,-1),
(1,2),
(2,-1),
(2,1)六种.
-1 1 2
-1
1
2
(-1,1)
(-1,2)
(1,-1)
(1,2)
(2,-1)
(2,1)
19.一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y.
(1)用列表法或树状图法,列出点M(x,y)的所有可能结果;
(2)用树状图法
-1
1
2
1
2
-1
2
-1
1
∴点M的所有可能结果有:
(-1,1),
(-1,2),
(1,-1),
(1,2),
(2,-1),
(2,1)六种.
19.一个不透明的口袋中有三个完全相同的小球,球上分别标有数字-1,1,2,第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y.
(2)求点M(x,y)在双曲线y=- 上的概率.
2
x
∴结果有6种可能性,且出现的可能性相等,
其中符合条件的有2种.
∴P=
2
6
1
3
=
∴点M(x,y)在双曲线上的概率为 .
1
3
(2)
