苏教版五年级下册数学3.3 3的倍数的特征(课件)(共25张PPT)
文档属性
| 名称 | 苏教版五年级下册数学3.3 3的倍数的特征(课件)(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 10:43:25 | ||
图片预览





文档简介
(共25张PPT)
因数和倍数
3的倍数的特征
苏教版五年级下册数学
1.探索3的倍数的特征,能判断一个数是不是3的倍
数。
2.经历探究3的倍数特征的过程,体会归纳思想,能
运用3的倍数特征来解决生活中的一些实际问题。
3.在探索活动中感受学习数学的乐趣,发展分析、
比较、猜测、验证的能力。
学习目标
按要求写出符合要求的数。
一个四位数235 :
(1)要使它是2的倍数, 里可以填: 。
(2)要使它是5的倍数, 里可以填: 。
(3)要使它既是2的倍数又有因数5倍数, 里可以填: 。
0,2,4,6,8
0,5
0
复习导入
5
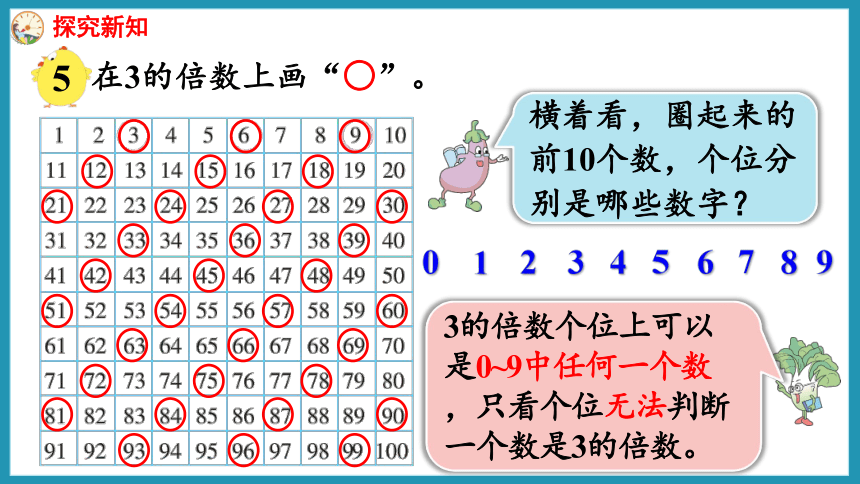
在3的倍数上画“○”。
横着看,圈起来的前10个数,个位分别是哪些数字?
3
6
9
2
5
8
1
4
7
0
3的倍数个位上可以是0~9中任何一个数,只看个位无法判断一个数是3的倍数。
探究新知
百 十 个
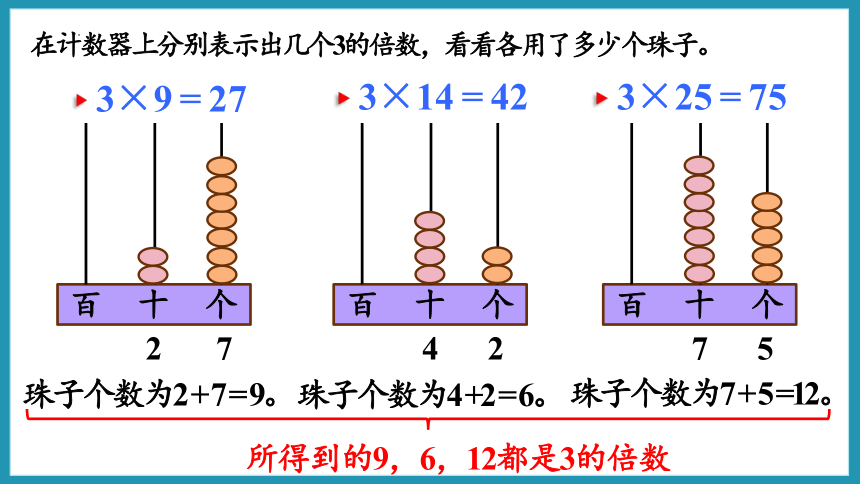
在计数器上分别表示出几个3的倍数,看看各用了多少个珠子。
2 7
珠子个数为2 + 7 = 9。
百 十 个
4 2
百 十 个
7 5
珠子个数为4 +2 = 6。
珠子个数为7 + 5 =12。
所得到的9,6,12都是3的倍数
3×9=27
3×14=42
3×25=75
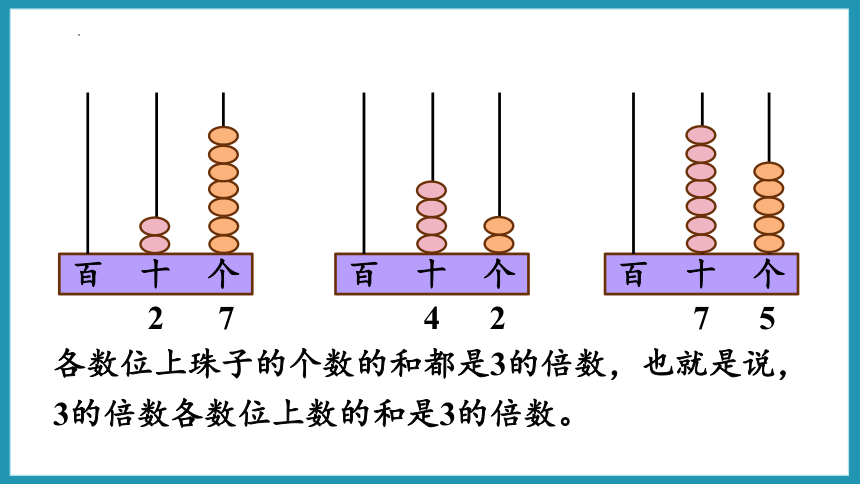
各数位上珠子的个数的和都是3的倍数,也就是说,3的倍数各数位上数的和是3的倍数。
百 十 个
2 7
百 十 个
4 2
百 十 个
7 5
213
2+1+3=6
213÷3=71
741
7+4+1=12
741÷3=247
1566
1+5+6+6=18
1566÷3=522
再找几个比较大的 3 的倍数,并在计数器上表示出来。算一算,每个数所用珠的个数各是多少?你有什么发现?
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
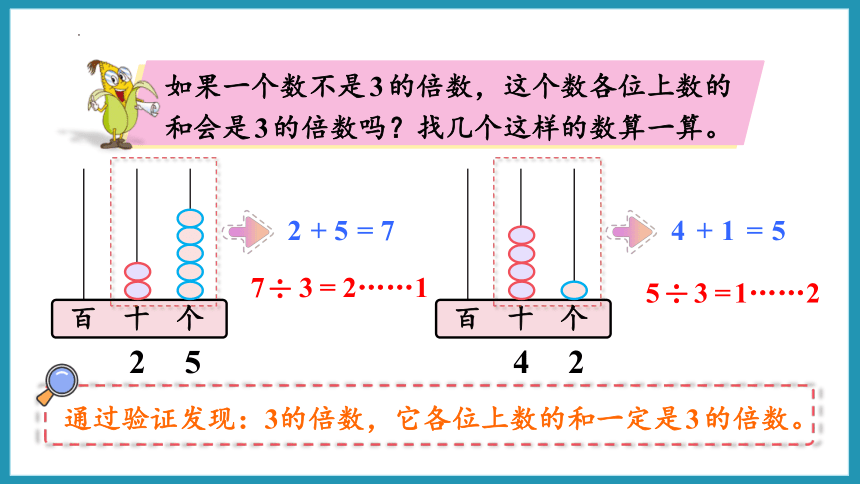
如果一个数不是3的倍数,这个数各位上数的和会是3的倍数吗?找几个这样的数算一算。
百
十
个
2
5
2
5
+
=
7
百
十
个
4
2
4
1
+
=
5
7
3
÷
=
2……1
5
3
÷
=
1……2
通过验证发现:3的倍数,它各位上数的和一定是3的倍数。
245
2+4+5=11
245÷3=81……2
679
6+7+9=22
679÷3=226……1
4580
4+5+8+0=17
4580÷3=1526……2
再找几个比较大的 不是3 的倍数,并在计数器上表示出来。算一算,每个数所用珠的个数各是多少?你有什么发现?
不是3的倍数的数,各位上的数的和也不是3的倍数。
6的因数有1,2,3,6,这几个因数之间的关系是: 1+2+3=6。像6这样的数叫做完全数(也叫做完美数)。
公元前6世纪,古希腊的毕达哥拉斯已经知道6和28是完全数。公元1世纪,尼克马修斯发现第3、4个完全数是496、8128。而第5个完全数直到1000多年后的15世纪才被发现。
随着计算机的问世,寻找完全数的工作较大进展。目前一共发现的47个完全数都是偶数,个位上都是6或8。
1.不计算,直接判断下面算式有没有余数,没有余数的画
“√”,有余数的画“ ”。
34÷3( ) 207÷3( √ )
71÷3( ) 741÷3( √ )
984÷3( √ ) 210÷3( √ )
√
√
√
√
课堂练习
(1)组成是3的倍数的两位数。
78、87、30
(2)组成是3的倍数的三位数。
708、780、738、783、807、870、837、873、378、387
2.按要求组数。
7 0 3 8
4,12,8,30,24,40,120
3. 按要求把下列各数填入相应的圈里。
4,12,25,8,30,45,24,40,120
12,30,45,24,120
25,30,45,40,120
12,30,24,120
30,120
4. 用哪种盒子装正好装完
用装3块的盒子或装5块的盒子都能正好装完。
[提示]405是3和5的倍数,不是2的倍数。
5. 41至少减去几才是3的倍数 50至少加上几才是3的倍数
41÷3=13……2
41至少减去2才是3的倍数。
50÷3=16……2 3-2=1
50至少加上1才是3的倍数。
[提示]先用41和50分别除以3求得余数,再根据余数判断加上几或减去几。
6.秦始皇陵兵马俑是世界文化遗产,其中三号坑中有68个兵马
俑,2个2个地数,能正好数完吗?如果3个3个地数,至少减少
几个才能正好数完?
2个2个地数,能正好数完。3个3个地数,至少减少2个
才能正好数完。
7.王阿姨买了225块月饼,想装在一些盒子里,有如图所示
的三种类型的盒子。
装在几号盒子里刚好装满且没有剩余?需要多少个这种类型的盒子?
225不是2的倍数,225是3和5的倍数,所以装在②号
或③号盒子里刚好装满且没有剩余。
225÷3=75(个)
225÷5=45(个)
答:装在②号或③号盒子里刚好装满且没有剩余,需要
75个②号盒子或45个③号盒子。
8. 唐老师在体育课上给五(3)班的同学分组,每3人一组,最后还多出2人。已知这个班的人数在40~51之间,则这个班可能有多少人
这个班可能有41人、44人、47人或50人。
[提示]人数比3的倍数多2,这里特别要注意的是3的倍数中的39,39+2=41(人),也在40~51之间,再用41依次加3。
提升练习
9. 三位数4 是一个偶数,同时是3和5的倍数,这样的三位数最小是多少 最大呢
最小:420
最大:480
[提示]因为这个三位数是偶数,所以这个三位数是2的倍数。因为这个三位数同时是5的倍数,所以它的个位上是0。最后根据3的倍数的特征确定十位上的数。
10. 把122连续写多少次所组成的数有因数3,并且这个数最小 请写出这个数。
3次
122122122
[提示]写1次时,各个数位上数的和为5;写2次时,各个数位上数的和为10;写3次时,各个数位上数的和为15;此时有因数3,所以这个数最小是122122122。
1. 一个两位数不是3的倍数,也不是6和9的倍数,加上8后就同时是3,6,9的倍数。这个两位数最大是
( )。
82
[提示]用倒推的方法,先求出同时是3,6,9的倍数的最大两位数是90,再用90减去8就是所求的两位数。
思维拓展
2. 的方框里最小填几时,这个数是3的倍数
2
[提示]2×2021=4042,4+0+4+2=10,因此在 里填2,5,8时,这个数是3的倍数, 里最小填2。
3.将自然数1、2、3、4、5、6、7、8、9依次重复写下去,得
到一个多位数123456789123456789……一共是2024位,这个数
是3的倍数吗?
2024÷9=224……8
(1+2+3+4+5+6+7+8+9)×224+1+2+3+4+
5+6+7+8=10116
1+0+1+1+6=9
9是3的倍数。
答:这个数是3的倍数。
这节课你有什么收获?
3的倍数特征
一个数的各个数位上的数字之和是3的倍数,这个数就一定是3的倍数。
课堂小结
这节课你有什么收获?
判断一个数是不是3的倍数,还可以用“筛选法”把各个数位上的数先筛去3的倍数,若剩下的数的和是3的倍数,则原来的数就是3的倍数,否则就不是。
课堂小结
因数和倍数
3的倍数的特征
苏教版五年级下册数学
1.探索3的倍数的特征,能判断一个数是不是3的倍
数。
2.经历探究3的倍数特征的过程,体会归纳思想,能
运用3的倍数特征来解决生活中的一些实际问题。
3.在探索活动中感受学习数学的乐趣,发展分析、
比较、猜测、验证的能力。
学习目标
按要求写出符合要求的数。
一个四位数235 :
(1)要使它是2的倍数, 里可以填: 。
(2)要使它是5的倍数, 里可以填: 。
(3)要使它既是2的倍数又有因数5倍数, 里可以填: 。
0,2,4,6,8
0,5
0
复习导入
5
在3的倍数上画“○”。
横着看,圈起来的前10个数,个位分别是哪些数字?
3
6
9
2
5
8
1
4
7
0
3的倍数个位上可以是0~9中任何一个数,只看个位无法判断一个数是3的倍数。
探究新知
百 十 个
在计数器上分别表示出几个3的倍数,看看各用了多少个珠子。
2 7
珠子个数为2 + 7 = 9。
百 十 个
4 2
百 十 个
7 5
珠子个数为4 +2 = 6。
珠子个数为7 + 5 =12。
所得到的9,6,12都是3的倍数
3×9=27
3×14=42
3×25=75
各数位上珠子的个数的和都是3的倍数,也就是说,3的倍数各数位上数的和是3的倍数。
百 十 个
2 7
百 十 个
4 2
百 十 个
7 5
213
2+1+3=6
213÷3=71
741
7+4+1=12
741÷3=247
1566
1+5+6+6=18
1566÷3=522
再找几个比较大的 3 的倍数,并在计数器上表示出来。算一算,每个数所用珠的个数各是多少?你有什么发现?
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
如果一个数不是3的倍数,这个数各位上数的和会是3的倍数吗?找几个这样的数算一算。
百
十
个
2
5
2
5
+
=
7
百
十
个
4
2
4
1
+
=
5
7
3
÷
=
2……1
5
3
÷
=
1……2
通过验证发现:3的倍数,它各位上数的和一定是3的倍数。
245
2+4+5=11
245÷3=81……2
679
6+7+9=22
679÷3=226……1
4580
4+5+8+0=17
4580÷3=1526……2
再找几个比较大的 不是3 的倍数,并在计数器上表示出来。算一算,每个数所用珠的个数各是多少?你有什么发现?
不是3的倍数的数,各位上的数的和也不是3的倍数。
6的因数有1,2,3,6,这几个因数之间的关系是: 1+2+3=6。像6这样的数叫做完全数(也叫做完美数)。
公元前6世纪,古希腊的毕达哥拉斯已经知道6和28是完全数。公元1世纪,尼克马修斯发现第3、4个完全数是496、8128。而第5个完全数直到1000多年后的15世纪才被发现。
随着计算机的问世,寻找完全数的工作较大进展。目前一共发现的47个完全数都是偶数,个位上都是6或8。
1.不计算,直接判断下面算式有没有余数,没有余数的画
“√”,有余数的画“ ”。
34÷3( ) 207÷3( √ )
71÷3( ) 741÷3( √ )
984÷3( √ ) 210÷3( √ )
√
√
√
√
课堂练习
(1)组成是3的倍数的两位数。
78、87、30
(2)组成是3的倍数的三位数。
708、780、738、783、807、870、837、873、378、387
2.按要求组数。
7 0 3 8
4,12,8,30,24,40,120
3. 按要求把下列各数填入相应的圈里。
4,12,25,8,30,45,24,40,120
12,30,45,24,120
25,30,45,40,120
12,30,24,120
30,120
4. 用哪种盒子装正好装完
用装3块的盒子或装5块的盒子都能正好装完。
[提示]405是3和5的倍数,不是2的倍数。
5. 41至少减去几才是3的倍数 50至少加上几才是3的倍数
41÷3=13……2
41至少减去2才是3的倍数。
50÷3=16……2 3-2=1
50至少加上1才是3的倍数。
[提示]先用41和50分别除以3求得余数,再根据余数判断加上几或减去几。
6.秦始皇陵兵马俑是世界文化遗产,其中三号坑中有68个兵马
俑,2个2个地数,能正好数完吗?如果3个3个地数,至少减少
几个才能正好数完?
2个2个地数,能正好数完。3个3个地数,至少减少2个
才能正好数完。
7.王阿姨买了225块月饼,想装在一些盒子里,有如图所示
的三种类型的盒子。
装在几号盒子里刚好装满且没有剩余?需要多少个这种类型的盒子?
225不是2的倍数,225是3和5的倍数,所以装在②号
或③号盒子里刚好装满且没有剩余。
225÷3=75(个)
225÷5=45(个)
答:装在②号或③号盒子里刚好装满且没有剩余,需要
75个②号盒子或45个③号盒子。
8. 唐老师在体育课上给五(3)班的同学分组,每3人一组,最后还多出2人。已知这个班的人数在40~51之间,则这个班可能有多少人
这个班可能有41人、44人、47人或50人。
[提示]人数比3的倍数多2,这里特别要注意的是3的倍数中的39,39+2=41(人),也在40~51之间,再用41依次加3。
提升练习
9. 三位数4 是一个偶数,同时是3和5的倍数,这样的三位数最小是多少 最大呢
最小:420
最大:480
[提示]因为这个三位数是偶数,所以这个三位数是2的倍数。因为这个三位数同时是5的倍数,所以它的个位上是0。最后根据3的倍数的特征确定十位上的数。
10. 把122连续写多少次所组成的数有因数3,并且这个数最小 请写出这个数。
3次
122122122
[提示]写1次时,各个数位上数的和为5;写2次时,各个数位上数的和为10;写3次时,各个数位上数的和为15;此时有因数3,所以这个数最小是122122122。
1. 一个两位数不是3的倍数,也不是6和9的倍数,加上8后就同时是3,6,9的倍数。这个两位数最大是
( )。
82
[提示]用倒推的方法,先求出同时是3,6,9的倍数的最大两位数是90,再用90减去8就是所求的两位数。
思维拓展
2. 的方框里最小填几时,这个数是3的倍数
2
[提示]2×2021=4042,4+0+4+2=10,因此在 里填2,5,8时,这个数是3的倍数, 里最小填2。
3.将自然数1、2、3、4、5、6、7、8、9依次重复写下去,得
到一个多位数123456789123456789……一共是2024位,这个数
是3的倍数吗?
2024÷9=224……8
(1+2+3+4+5+6+7+8+9)×224+1+2+3+4+
5+6+7+8=10116
1+0+1+1+6=9
9是3的倍数。
答:这个数是3的倍数。
这节课你有什么收获?
3的倍数特征
一个数的各个数位上的数字之和是3的倍数,这个数就一定是3的倍数。
课堂小结
这节课你有什么收获?
判断一个数是不是3的倍数,还可以用“筛选法”把各个数位上的数先筛去3的倍数,若剩下的数的和是3的倍数,则原来的数就是3的倍数,否则就不是。
课堂小结
