苏教版五年级下册数学4.7 分数的基本性质(课件)(共28张PPT)
文档属性
| 名称 | 苏教版五年级下册数学4.7 分数的基本性质(课件)(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
分数的意义和性质
分数的基本性质
苏教版五年级下册数学
1.经历探索分数基本性质的过程,初步理解分数的基本性质。
2.能应用分数的基本性质,把一个分数化成指定分母或分子而大小不变的分数。
3.在观察、操作、思考和交流等活动中,培养分析、综合、抽象、概括的能力,体验数学学习的乐趣。
学习目标
动物园有3只猴子,管理员拿来一个西瓜分给它们吃:西瓜平均分,每只吃3块怎么样?小猴子们很不高兴,都嫌太少了。管理员:那西瓜平均分,每只4块怎么样?小猴子们都很高兴。同学们,你们说,猴子吃到的西瓜变多了吗?为什么?
没有变多,因为每只猴子吃得还是这个西瓜的三分之一。
课堂导入
11
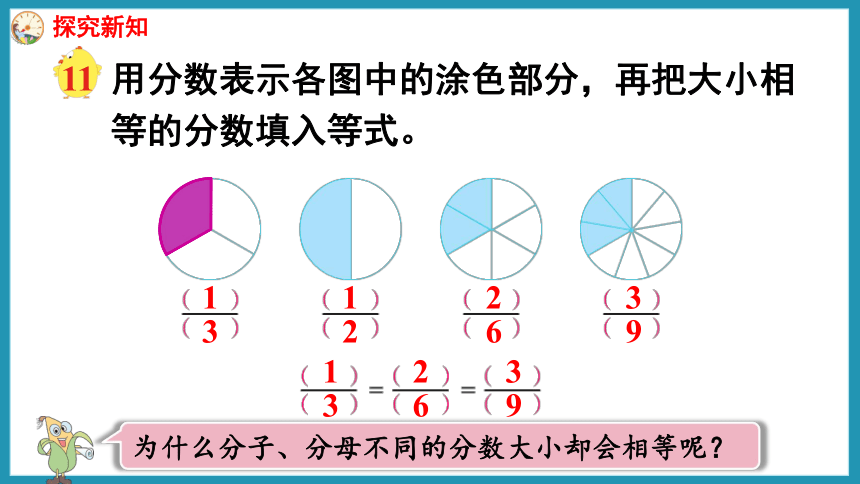
用分数表示各图中的涂色部分,再把大小相等的分数填入等式。
3
1
2
1
6
2
9
3
3
1
6
2
9
3
探究新知
为什么分子、分母不同的分数大小却会相等呢?
把一张正方形纸对折, 涂色表示它的 。
继续对折,每次找出一个和 相等的分数,并用等式表示。
请同学们借助学具,自己动手折一折吧!
12
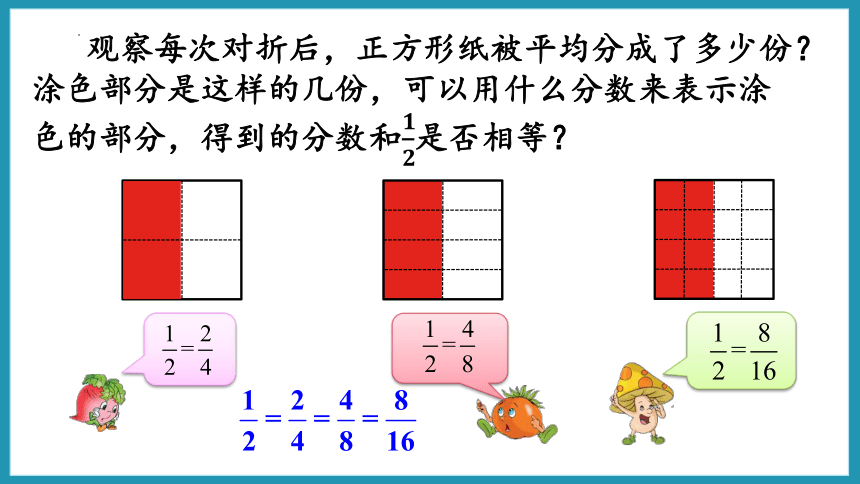
观察每次对折后,正方形纸被平均分成了多少份?涂色部分是这样的几份,可以用什么分数来表示涂色的部分,得到的分数和是否相等?
=
=
=
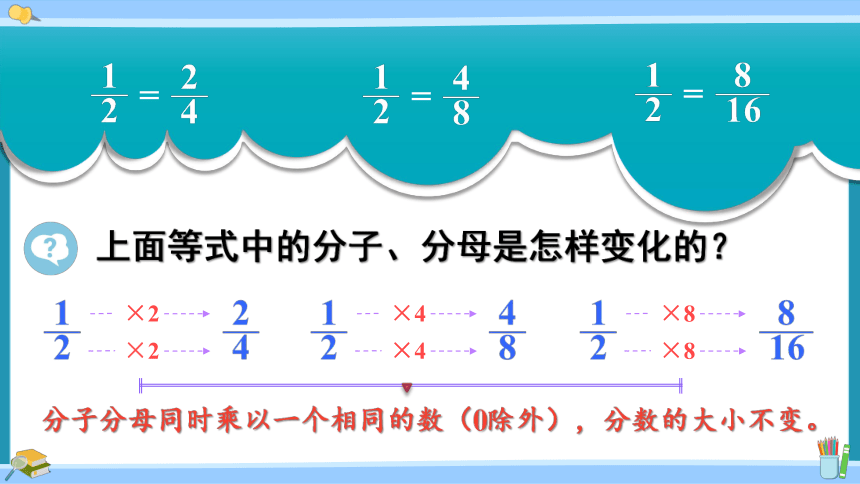
上面等式中的分子、分母是怎样变化的?
×2
×2
×4
×4
×8
×8
分子分母同时乘以一个相同的数(0除外),分数的大小不变。
完成下面的填空。
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
2
2
2
2
4
4
4
4
8
8
8
8
4
2
8
4
16
8
1
3
2
6
3
9
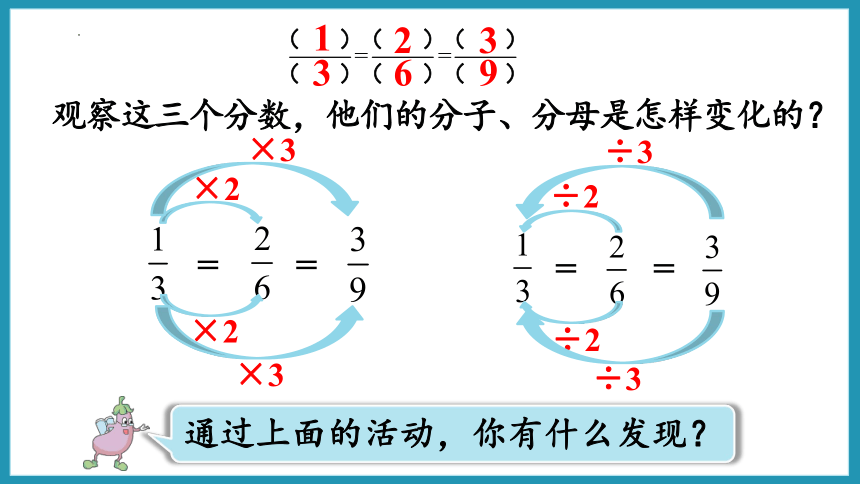
观察这三个分数,他们的分子、分母是怎样变化的?
×2
×2
×3
×3
= =
÷2
÷2
÷3
÷3
= =
通过上面的活动,你有什么发现?
×2
×2
×2
×2
×2
×2
2÷
2÷
2÷
2÷
2÷
2÷
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
根据分数与除法的关系,你能用除法中商不变的规律来说明分数的基本性质吗?
回顾发现分数基本性质的过程,你有哪些收获?
学习过程中,要注意沟通知识之间的联系。
画图和操作能帮助我们发现规律。
一个分数,有无数个与它相等的分数。
1. 先用分数表示下面各图中的涂色部分,再用适当的符号把三个分数连接起来。
= =
课堂练习
2. 涂一涂,填一填。
=
=
3. 在括号里填适当的数。
= =
= =
==
==
==
==
==
====
====
4. (1)把和都化成分子是6而大小不变的分数。
=
=
(2)把和都化成分母是10而大小不变的分数。
=
=
5. 如果一个分数的分母除以3,分子不变,那么分数的大小有什么变化 如果分子乘3,分母不变呢
分数扩大到原来的3倍。
分数扩大到原来的3倍。
6.唐僧师徒四人分吃一个大西瓜,唐僧吃了这个西瓜的,
孙悟空吃了这个西瓜的,沙和尚吃了这个西瓜的,猪八
戒吃了这个西瓜的。他们四人谁吃得多?
== ==
== ===
答:他们四人吃得一样多。
7. 把的分子加2n后,要使分数的大小不变,分母应该增加多少
2n÷n=2 2×m=2m
[提示]分母加的数应该是原来分母的2倍。
提升练习
8. 一个分数的分子、分母之和是40,将分子、分母都除以同一个数,得到一个新的分数是。原来的分数是几分之几
40÷(7+1)=5
==
9. 一个分数,分子缩小到原来的,分母缩小到原来的,这个分数变为。求原来这个分数。
=
[提示]本题运用倒推法求出原来分数的大小。
1. 一个分数,分母比分子大12,它与相等。这个分数是多少
[提示]原来分母与分子的差是12,12÷(5-2)=4,=。
思维拓展
2.一个分数与相等,且它的分子加上6后,得到的分数等于1。这个分数原来是多少?
13-11=2 6÷2=3
==
的分子加上6后,变成=1。
答:这个分数原来是。
3. 一个分数,分子加上1后得;分子减去1后得。这个分数是多少
[提示]因为=,=,所以这个分数是。
4.一个分数的分子与分母的和是86,如果分子和分母都减去9,那么得到的分数与相等。原来的分数是多少?
86-9-9=68 8+9=17
现在的分子:68÷17×8=32
现在的分母:68-32=36
原来的分数:=
答:原来的分数是。
这节课你有什么收获?
分数的分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变。这是分数的基本性质。
课堂小结
分数的意义和性质
分数的基本性质
苏教版五年级下册数学
1.经历探索分数基本性质的过程,初步理解分数的基本性质。
2.能应用分数的基本性质,把一个分数化成指定分母或分子而大小不变的分数。
3.在观察、操作、思考和交流等活动中,培养分析、综合、抽象、概括的能力,体验数学学习的乐趣。
学习目标
动物园有3只猴子,管理员拿来一个西瓜分给它们吃:西瓜平均分,每只吃3块怎么样?小猴子们很不高兴,都嫌太少了。管理员:那西瓜平均分,每只4块怎么样?小猴子们都很高兴。同学们,你们说,猴子吃到的西瓜变多了吗?为什么?
没有变多,因为每只猴子吃得还是这个西瓜的三分之一。
课堂导入
11
用分数表示各图中的涂色部分,再把大小相等的分数填入等式。
3
1
2
1
6
2
9
3
3
1
6
2
9
3
探究新知
为什么分子、分母不同的分数大小却会相等呢?
把一张正方形纸对折, 涂色表示它的 。
继续对折,每次找出一个和 相等的分数,并用等式表示。
请同学们借助学具,自己动手折一折吧!
12
观察每次对折后,正方形纸被平均分成了多少份?涂色部分是这样的几份,可以用什么分数来表示涂色的部分,得到的分数和是否相等?
=
=
=
上面等式中的分子、分母是怎样变化的?
×2
×2
×4
×4
×8
×8
分子分母同时乘以一个相同的数(0除外),分数的大小不变。
完成下面的填空。
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
2
2
2
2
4
4
4
4
8
8
8
8
4
2
8
4
16
8
1
3
2
6
3
9
观察这三个分数,他们的分子、分母是怎样变化的?
×2
×2
×3
×3
= =
÷2
÷2
÷3
÷3
= =
通过上面的活动,你有什么发现?
×2
×2
×2
×2
×2
×2
2÷
2÷
2÷
2÷
2÷
2÷
分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
根据分数与除法的关系,你能用除法中商不变的规律来说明分数的基本性质吗?
回顾发现分数基本性质的过程,你有哪些收获?
学习过程中,要注意沟通知识之间的联系。
画图和操作能帮助我们发现规律。
一个分数,有无数个与它相等的分数。
1. 先用分数表示下面各图中的涂色部分,再用适当的符号把三个分数连接起来。
= =
课堂练习
2. 涂一涂,填一填。
=
=
3. 在括号里填适当的数。
= =
= =
==
==
==
==
==
====
====
4. (1)把和都化成分子是6而大小不变的分数。
=
=
(2)把和都化成分母是10而大小不变的分数。
=
=
5. 如果一个分数的分母除以3,分子不变,那么分数的大小有什么变化 如果分子乘3,分母不变呢
分数扩大到原来的3倍。
分数扩大到原来的3倍。
6.唐僧师徒四人分吃一个大西瓜,唐僧吃了这个西瓜的,
孙悟空吃了这个西瓜的,沙和尚吃了这个西瓜的,猪八
戒吃了这个西瓜的。他们四人谁吃得多?
== ==
== ===
答:他们四人吃得一样多。
7. 把的分子加2n后,要使分数的大小不变,分母应该增加多少
2n÷n=2 2×m=2m
[提示]分母加的数应该是原来分母的2倍。
提升练习
8. 一个分数的分子、分母之和是40,将分子、分母都除以同一个数,得到一个新的分数是。原来的分数是几分之几
40÷(7+1)=5
==
9. 一个分数,分子缩小到原来的,分母缩小到原来的,这个分数变为。求原来这个分数。
=
[提示]本题运用倒推法求出原来分数的大小。
1. 一个分数,分母比分子大12,它与相等。这个分数是多少
[提示]原来分母与分子的差是12,12÷(5-2)=4,=。
思维拓展
2.一个分数与相等,且它的分子加上6后,得到的分数等于1。这个分数原来是多少?
13-11=2 6÷2=3
==
的分子加上6后,变成=1。
答:这个分数原来是。
3. 一个分数,分子加上1后得;分子减去1后得。这个分数是多少
[提示]因为=,=,所以这个分数是。
4.一个分数的分子与分母的和是86,如果分子和分母都减去9,那么得到的分数与相等。原来的分数是多少?
86-9-9=68 8+9=17
现在的分子:68÷17×8=32
现在的分母:68-32=36
原来的分数:=
答:原来的分数是。
这节课你有什么收获?
分数的分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变。这是分数的基本性质。
课堂小结
