苏教版小学数学五年级下册3.7 《练习六》课件(共23张PPT)
文档属性
| 名称 | 苏教版小学数学五年级下册3.7 《练习六》课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
因数和倍数
练习六
苏教版五年级下册数学
质数和合数
1.一个数,如果只有1和它本身两个因数,这样的数叫作质数(或素数)。
2.一个数,如果除了1和本身还有别的因数,这样的数 叫作合数。
知识回顾
3. 1既不是质数,也不是合数。
质数与合数的个数都是无限的,没有最大的质数或合数。最小的质数是2,最小的合数是4。其中,2是唯一一个既是偶数又是质数的数。
自然数(不包括0)可以分成质数、合数和1三大类。
知识回顾
分解质因数
1.质因数:如果一个数的因数是质数,这个因数就是它的质因数。
2.分解质因数:把一个合数用质数相乘的形式表示出来,叫作分解质因数。
3.质因数是一个具体的数。分解质因数是把一个合数拆分成几个质数相乘的形式的过程。
知识回顾
方法一:枝状图分解法
30
( )
( )
( )
( )
×
×
2
15
3
5
30=2×3×5
方法二:短除法
3 0
2
1 5
3
5
30=2×3×5
把30分解质因数
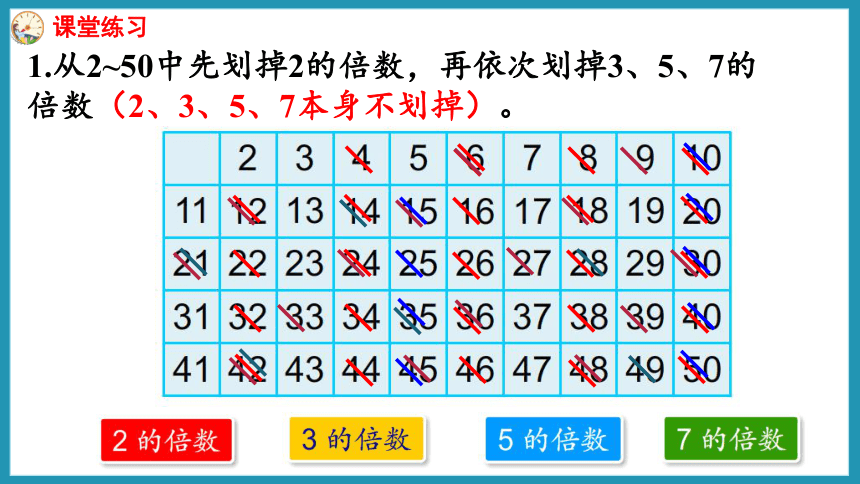
1.从2~50中先划掉2的倍数,再依次划掉3、5、7的倍数(2、3、5、7本身不划掉)。
课堂练习
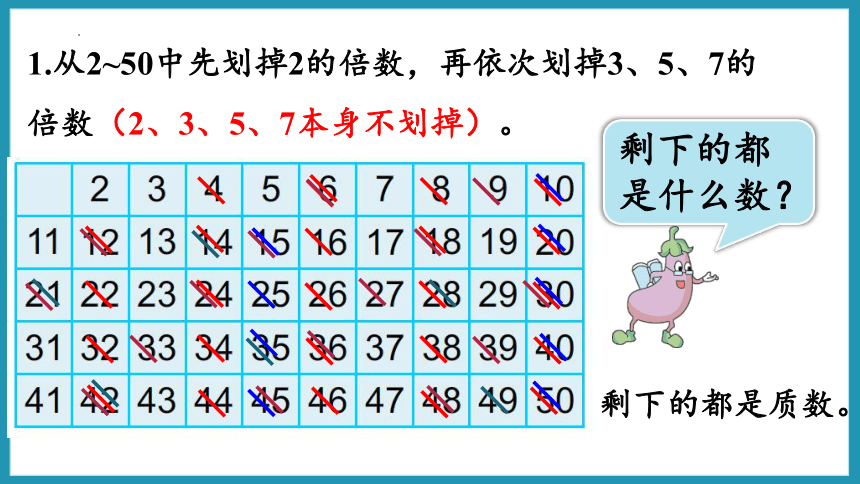
1.从2~50中先划掉2的倍数,再依次划掉3、5、7的倍数(2、3、5、7本身不划掉)。
剩下的都是什么数?
剩下的都是质数。
2.填一填。
(1)在1~9这些数中,相邻两个数都是质数的是( 2 )和
( 3 ),相邻两个数都是合数的是( 8 )和
( 9 )。
(2)10以内的质数的积是( 210 ),20以内的质数的和是
( 77 )。
(3)一个数的最小倍数是34,这个数是( 34 ),把这个
数分解质因数是( 34=2×17 )。
2
3
8
9
210
77
34
34=2×17
(4)一个三位数,百位上的数是奇数也是合数,十位上的数
是一位数中最大的质数,个位上的数是最小的合数,这个数是
( 974 )。
974
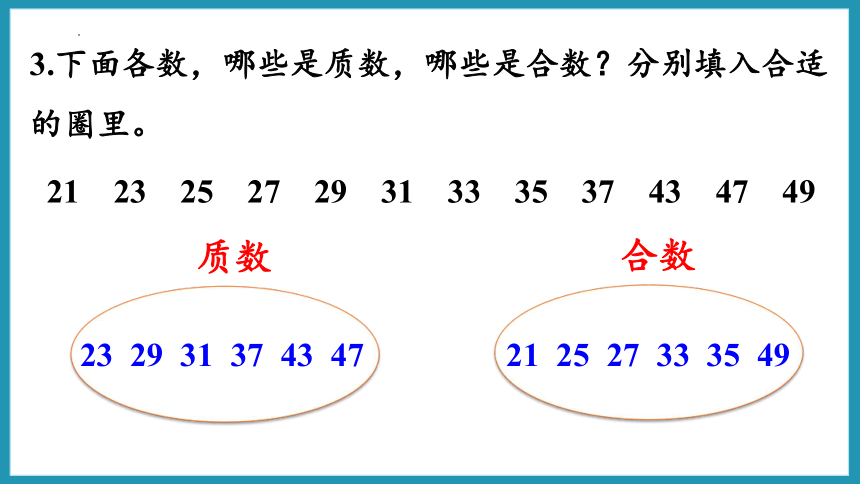
3.下面各数,哪些是质数,哪些是合数?分别填入合适的圈里。
21 23 25 27 29 31 33 35 37 43 47 49
质数
合数
23 29 31 37 43 47
21 25 27 33 35 49
4.下面各数是由哪些质数相乘得到的?
15=( )×( )
26=( )×( )
5
3
15
3
5
13
2
26
2
13
42=( )×( )×( )
66=( )×( )×( )
4.下面各数是由哪些质数相乘得到的?
21
2
42
7
3
3 3
2
6 6
1 1
3
2
7
3
2
11
3
5.在括号里填上不同的质数。
19=( 17 )+( 2 )
21=( 3 )×( 7 )
38=( 31 )+( 7 )
110=( 2 )×( 5 )×( 11 )
17
2
3
7
31
7
2
5
11
6.我是一个四位数,同时是2和5的倍数。我的最高位上的
数是最小的质数,百位上的数是一位数中最大的合数,十
位上的数既不是质数,也不是合数。我是( 2910 )。
7.向阳小学跆拳道社的同学们排成长方形队伍进行训
练,长方形队伍的行数和列数都是质数,有三名同学分别数出
长方形队伍的人数为68人、77人、70人,只有一名同学数对
了,长方形队伍的人数是多少?为什么?
长方形队伍的人数是77人。因为68=2×2×17,77=
7×11,70=2×5×7,三个数分别分解质因数后,只有
77可以分解成两个质数相乘的形式,所以长方形队伍的
人数是77人。
2910
8. 学校数学老师办公室最近装了一部电话,电话号码如下:
A B C D E F G H
A:10以内最大的奇数。
B:两个连续自然数且都是质数的乘积。
C:既不是质数也不是合数,而且不是0。
提升练习
D:10以内最大的质数。
E:最小的合数。
F:既是质数又是奇数的最小数。
G:最小的质数。
H:既是合数又是奇数。
你知道电话号码是多少吗 快来猜一猜吧。
96174329
9.陈小英代表五(2)班参加学校的数学竞赛。你知道陈小英
的分数、名次和年龄分别是多少吗?
2134=2×11×97
因为陈小英的分数、名次和年龄都是质数,所以陈小英
的分数是97分,名次是第2名,年龄是11岁。
10. 一个长方形的长和宽均为质数,并且周长是36厘米。这个长方形的面积最大是多少平方厘米
36÷2=18(厘米)
18=5+13=7+11
11×7=77(平方厘米)
[提示]两个数的和是18时,这两个数相差越小乘积越大。
1.有一个三位数,它的个位上的数字和百位上的数字之和
是10,且个位上的数字既是偶数又是质数,又知道这个三
位数是21的倍数,求这个三位数是多少。
这个三位数是882。
思维拓展
2. 三个小朋友,他们的年龄正好是三个连续的自然数,且他们年龄的乘积是60,这三个小朋友分别是多少岁?
解析:三个小朋友的年龄正好是三个连续的自然数,并且它们的乘积是60,可以先把60 分解质因数,然后把分解的结果写成三个连续自然数的积的形式,即可求得这三个小朋友的年龄。
60=2×2×3×5=3×4×5
答:这三个小朋友分别是3 岁、4 岁和5 岁。
3. 班主任李老师带领五年级一班的学生去植树,学生恰好被平均分成 4 组,师生一共植树 174 棵。如果李老师和学生每人植树的棵数都相同,那么五年级一班有学生多少人?每人植树多少棵?
174=2×3×29
29-1=28(人)
28 人恰好能被平均分成4 组。
174÷29=6(棵)
答:五年级一班有学生28 人,每人植树6 棵。
200多年前,德国的数学家哥德巴赫发现每一个大于4的偶数都可以表示成两个奇素数之和,例如,6=3+3,8=3+5, 10=5+5,12=5+7。通过举例检验是完全可信的,但他却无法在理论上加以证明。于是,哥德巴赫于1742年6月7日写信给当时世界上最优秀的大数学家欧拉,请他帮助解决这个问题,欧拉回信表示:这个问题我虽然不能证明,但我确信它是正确的。同时,欧拉又补充指出:任何大于2的偶数都是两个素数之和。后来,这两个命题被合称为“哥德巴赫猜想”。
人们通常把数学誉为科学的皇后,而数论(研
究自然数性质的数学分支)是数学的皇冠。由于哥
德巴赫猜想的证明难度实在太高了,人们把这个猜
想比喻为“数学皇冠上的明珠”。在摘取“明珠”
的过程中,我国数学家做出了重要的贡献。1958~1962年,王元和潘承洞的研究取得了重大进展。1966年,陈景润更上一层楼,在“哥德巴赫猜想”的研究上取得了更加显著的进展,轰动了国内外数学界。他的研究成果被公认为最具有突破性和创造性,“是当代在哥德巴赫猜想的研究方面最好的成果”。
教你一招:
1.质数与合数的个数都是无限的,没有最大的质数
或合数。最小的质数是2,最小的合数是4。其中,
2是唯一一个既是偶数又是质数的数。
2.自然数(不包括0)可以分成质数、合数和1
大类。
课堂小结
因数和倍数
练习六
苏教版五年级下册数学
质数和合数
1.一个数,如果只有1和它本身两个因数,这样的数叫作质数(或素数)。
2.一个数,如果除了1和本身还有别的因数,这样的数 叫作合数。
知识回顾
3. 1既不是质数,也不是合数。
质数与合数的个数都是无限的,没有最大的质数或合数。最小的质数是2,最小的合数是4。其中,2是唯一一个既是偶数又是质数的数。
自然数(不包括0)可以分成质数、合数和1三大类。
知识回顾
分解质因数
1.质因数:如果一个数的因数是质数,这个因数就是它的质因数。
2.分解质因数:把一个合数用质数相乘的形式表示出来,叫作分解质因数。
3.质因数是一个具体的数。分解质因数是把一个合数拆分成几个质数相乘的形式的过程。
知识回顾
方法一:枝状图分解法
30
( )
( )
( )
( )
×
×
2
15
3
5
30=2×3×5
方法二:短除法
3 0
2
1 5
3
5
30=2×3×5
把30分解质因数
1.从2~50中先划掉2的倍数,再依次划掉3、5、7的倍数(2、3、5、7本身不划掉)。
课堂练习
1.从2~50中先划掉2的倍数,再依次划掉3、5、7的倍数(2、3、5、7本身不划掉)。
剩下的都是什么数?
剩下的都是质数。
2.填一填。
(1)在1~9这些数中,相邻两个数都是质数的是( 2 )和
( 3 ),相邻两个数都是合数的是( 8 )和
( 9 )。
(2)10以内的质数的积是( 210 ),20以内的质数的和是
( 77 )。
(3)一个数的最小倍数是34,这个数是( 34 ),把这个
数分解质因数是( 34=2×17 )。
2
3
8
9
210
77
34
34=2×17
(4)一个三位数,百位上的数是奇数也是合数,十位上的数
是一位数中最大的质数,个位上的数是最小的合数,这个数是
( 974 )。
974
3.下面各数,哪些是质数,哪些是合数?分别填入合适的圈里。
21 23 25 27 29 31 33 35 37 43 47 49
质数
合数
23 29 31 37 43 47
21 25 27 33 35 49
4.下面各数是由哪些质数相乘得到的?
15=( )×( )
26=( )×( )
5
3
15
3
5
13
2
26
2
13
42=( )×( )×( )
66=( )×( )×( )
4.下面各数是由哪些质数相乘得到的?
21
2
42
7
3
3 3
2
6 6
1 1
3
2
7
3
2
11
3
5.在括号里填上不同的质数。
19=( 17 )+( 2 )
21=( 3 )×( 7 )
38=( 31 )+( 7 )
110=( 2 )×( 5 )×( 11 )
17
2
3
7
31
7
2
5
11
6.我是一个四位数,同时是2和5的倍数。我的最高位上的
数是最小的质数,百位上的数是一位数中最大的合数,十
位上的数既不是质数,也不是合数。我是( 2910 )。
7.向阳小学跆拳道社的同学们排成长方形队伍进行训
练,长方形队伍的行数和列数都是质数,有三名同学分别数出
长方形队伍的人数为68人、77人、70人,只有一名同学数对
了,长方形队伍的人数是多少?为什么?
长方形队伍的人数是77人。因为68=2×2×17,77=
7×11,70=2×5×7,三个数分别分解质因数后,只有
77可以分解成两个质数相乘的形式,所以长方形队伍的
人数是77人。
2910
8. 学校数学老师办公室最近装了一部电话,电话号码如下:
A B C D E F G H
A:10以内最大的奇数。
B:两个连续自然数且都是质数的乘积。
C:既不是质数也不是合数,而且不是0。
提升练习
D:10以内最大的质数。
E:最小的合数。
F:既是质数又是奇数的最小数。
G:最小的质数。
H:既是合数又是奇数。
你知道电话号码是多少吗 快来猜一猜吧。
96174329
9.陈小英代表五(2)班参加学校的数学竞赛。你知道陈小英
的分数、名次和年龄分别是多少吗?
2134=2×11×97
因为陈小英的分数、名次和年龄都是质数,所以陈小英
的分数是97分,名次是第2名,年龄是11岁。
10. 一个长方形的长和宽均为质数,并且周长是36厘米。这个长方形的面积最大是多少平方厘米
36÷2=18(厘米)
18=5+13=7+11
11×7=77(平方厘米)
[提示]两个数的和是18时,这两个数相差越小乘积越大。
1.有一个三位数,它的个位上的数字和百位上的数字之和
是10,且个位上的数字既是偶数又是质数,又知道这个三
位数是21的倍数,求这个三位数是多少。
这个三位数是882。
思维拓展
2. 三个小朋友,他们的年龄正好是三个连续的自然数,且他们年龄的乘积是60,这三个小朋友分别是多少岁?
解析:三个小朋友的年龄正好是三个连续的自然数,并且它们的乘积是60,可以先把60 分解质因数,然后把分解的结果写成三个连续自然数的积的形式,即可求得这三个小朋友的年龄。
60=2×2×3×5=3×4×5
答:这三个小朋友分别是3 岁、4 岁和5 岁。
3. 班主任李老师带领五年级一班的学生去植树,学生恰好被平均分成 4 组,师生一共植树 174 棵。如果李老师和学生每人植树的棵数都相同,那么五年级一班有学生多少人?每人植树多少棵?
174=2×3×29
29-1=28(人)
28 人恰好能被平均分成4 组。
174÷29=6(棵)
答:五年级一班有学生28 人,每人植树6 棵。
200多年前,德国的数学家哥德巴赫发现每一个大于4的偶数都可以表示成两个奇素数之和,例如,6=3+3,8=3+5, 10=5+5,12=5+7。通过举例检验是完全可信的,但他却无法在理论上加以证明。于是,哥德巴赫于1742年6月7日写信给当时世界上最优秀的大数学家欧拉,请他帮助解决这个问题,欧拉回信表示:这个问题我虽然不能证明,但我确信它是正确的。同时,欧拉又补充指出:任何大于2的偶数都是两个素数之和。后来,这两个命题被合称为“哥德巴赫猜想”。
人们通常把数学誉为科学的皇后,而数论(研
究自然数性质的数学分支)是数学的皇冠。由于哥
德巴赫猜想的证明难度实在太高了,人们把这个猜
想比喻为“数学皇冠上的明珠”。在摘取“明珠”
的过程中,我国数学家做出了重要的贡献。1958~1962年,王元和潘承洞的研究取得了重大进展。1966年,陈景润更上一层楼,在“哥德巴赫猜想”的研究上取得了更加显著的进展,轰动了国内外数学界。他的研究成果被公认为最具有突破性和创造性,“是当代在哥德巴赫猜想的研究方面最好的成果”。
教你一招:
1.质数与合数的个数都是无限的,没有最大的质数
或合数。最小的质数是2,最小的合数是4。其中,
2是唯一一个既是偶数又是质数的数。
2.自然数(不包括0)可以分成质数、合数和1
大类。
课堂小结
