苏教版五年级下册数学综合与实践 球的反弹高度课件(共28张PPT)
文档属性
| 名称 | 苏教版五年级下册数学综合与实践 球的反弹高度课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 11:37:24 | ||
图片预览







文档简介
(共28张PPT)
分数的意义和性质
综合与实践 球的反弹高度
苏教版五年级下册数学
通过实验收集数据、记录比较数据,能用分数表示球的反弹高度与下落高度的关系,进一步掌握求一个数是另一个数的几分之几的方法,加深对分数意义的理解。
经历操作实验、收集数据、计算比较等活动,感受用实验方法探究问题结论的过程,体会实验数据的重要性,积累基本活动经验,进一步发展数据分析观念。
学习目标
打篮球、踢足球、拍皮球等都是同学们喜爱的运动,大家有没有注意到这些球从高处落地后都会怎样?
球从高处落地后都会反弹。
课堂导入
通过上图中的活动,你想到了哪些问题?
如果把这些球,从同一高度自由落下,它们的反弹高度会一样吗?
如果同一个球,从不同的高度自由落下,反弹高度一样吗?
把它们从同一高度自由落下,哪种球反弹得高一些?
球的反弹高度和下落高度之间有什么关系?
选择一块靠墙的平地,在墙上量出一个高度并做上标记。再选择一个球从这个高度自由落下,在墙上标出球的反弹高度,量出结果并记录下来。
准备活动材料
一个皮球
卷尺
记录本
活动一 用皮球测反弹
活动内容:
组织活动
(1)确定投球、观察、测量和记录数据的同学。
(2)明确活动要求:①几次扔球的力度要一致,尽量让球自由落体;②观察和标记反弹高度的同学要认真,保持标记的位置尽量准确;③及时记录数据。
操作方法
(1)选一块靠墙的平地,在墙上量出三个不同的高度并做上标记。
(2)选择皮球从这三个不同的高度自由落下,在墙上标出球的反弹高度。
(3)量出结果并记录。
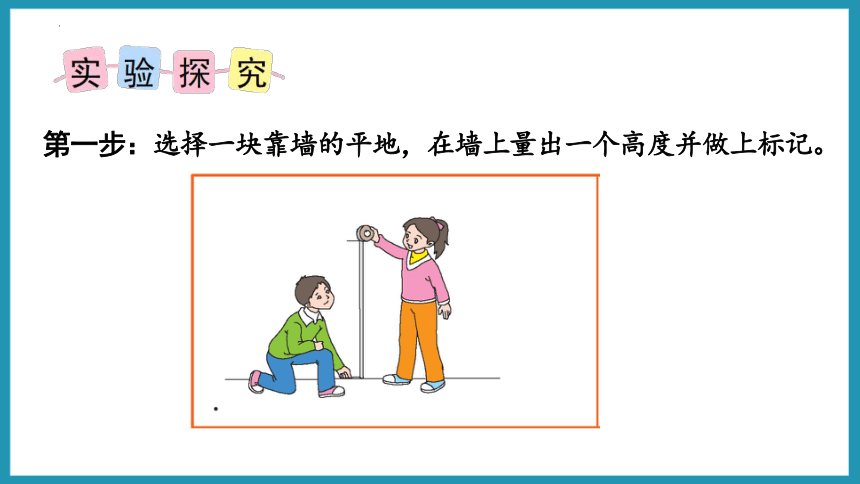
第一步:选择一块靠墙的平地,在墙上量出一个高度并做上标记。
第二步:让球的最下沿与墙上的高度标记齐平,松手,让球自由落下。
第三步:看清楚球的最下沿反弹的最高点,并迅速在墙上做上标记。
若看不清楚可以重复一次。
第四步:用尺子量出反弹高度并记录下来(测量结果取整厘米数,
以便于计算和比较)。
把球的上沿对齐墙上的刻度线,要看清球的反弹高度并迅速做好标记,测量要准确,记录的结果取整厘米数就可以了。
选择不同的高度做三次实验,记录量得的数据,并求出每次反弹的高度是下落高度的几分之几。
( )球 第一次 第二次 第三次
下落高度
反弹高度
反弹高度是下落高度的几分之几
皮
200厘米
240厘米
180厘米
80厘米
96厘米
72厘米
用同一个球做实验,你发现了什么?
球的反弹高度与下落的高度有关。
在同一个地点,同一个球从不同高度下落,其反弹高度是不一样的,但表示同一个球反弹高度与下落高度关系的分数大致不变,说明同一个球的弹性是一样的。
选择其他的球再做三次实验,记录实验的结果,并与同学交流。
( )球 第一次 第二次 第三次
下落高度
反弹高度
反弹高度是下落高度的几分之几
在小组内分享实验数据吧。
仍在刚才靠墙的平地,用排球和网球各做三次实验,记录实验的结果,并求出每次反弹的高度是下落高度的几分之几。
活动过程:
准备实验材料:
小组合作,通过实验标记、测量并记录实验结果,求出反弹高度是下落高度的几分之几。
网球
卷尺
记录本
羽毛球
( )球 第一次 第二次 第三次
下落高度
反弹高度
反弹高度是下落高度的几分之几
网
100厘米
120厘米
140厘米
50厘米
60厘米
70厘米
( )球 第一次 第二次 第三次
下落高度
反弹高度
反弹高度是下落高度的几分之几
排
100厘米
120厘米
140厘米
30厘米
36厘米
42厘米
用不同的球做实验,你发现了什么?
在同一个地点,不同的球从同一高度下落,其反弹高度一般不同,表示相应反弹高度与下落高度关系的分数也不同,说明不同的球的弹性是不一样的。
探究球的反弹高度与下落高度的关系时,要联系已学过的统计知识、测量方法以及本单元学过的分数知识;
日常生活中有很多有趣的数学问题,要善于用发现的眼光观察,并勇于探索;
解决一些实际问题时,需要认真实验才可能得到准确的数据和结论;
在实验中收集数据时,要注意准确操作、实事求是。收集的数据越多,越容易发现规律、获得结论。
通过这一次活动,你有什么收获?
同一种球的弹性主要取决于球内部所受到的压力,而压力的大小与球内充进的空气多少有关。在正式球类比赛时,对球的弹性都有明确的规定。例如,比赛用的篮球,从1.8米的高度自由落下后,第一次反弹的高度应大于1.2米、小于1.4米。
1. 填一填。
(1)同一个球从不同高度自由落地,反弹高度( 不同)。
(2)同一个球从不同高度下落,表示反弹高度与下落高度关系的分数大致( 相同 ),这说明同一个球的弹性是一样的。
不同
相同
(3)一个球从100米高度自由落下,每次落地后返弹回原高度的一半。反弹两次后,反弹的高度是100米的( )。
课堂练习
2. 一个球从50米高度自由落下,落地后反弹高度是24米,反弹高度是下落高度的几分之几
24÷50=
第一次 第二次 第三次
下落高度/厘米 200 240 180
反弹高度/厘米 80 96 72
反弹高度是下落高度的几分之几
(1)完成上表。 (2)通过计算比较,你发现了什么
(3)如果这个皮球从10米的高度落下,那么它第一次反弹的高度可能是多少米
(4)如果这个皮球落下后第一次反弹的高度是2米,那么这个皮球可能是从什么高度落下的
3. 下表是一个皮球从不同高度下落与反弹高度的测量记录。
(2)通过计算比较,你发现了什么
(3)如果这个皮球从10米的高度落下,那么它第一次反弹的高度可能是多少米
同一个球从不同高度下落,表示反弹高度与下落高度关系的分数相同。
10÷5×2=4(米)
(4)如果这个皮球落下后第一次反弹的高度是2米,那么这个皮球可能是从什么高度落下的
2÷2×5=5(米)
4. 在研究球的反弹高度的实验活动中,淘气让一个篮球从1.8米的高度自由落下。他一共做了5次实验,每次反弹的高度记录如下:(单位:米)
1.2 1.3 1.25 1.3 1.35
(1)这个篮球从1.8米的高度自由落下,平均每次的反弹高度是多少
(2)你觉得怎样可以让这个实验的数据更为准确
(1)这个篮球从1.8米的高度自由落下,平均每次的反弹高度是多少
(1.2+1.3+1.25+1.3+1.35)÷5=1.28(米)
(2)你觉得怎样可以让这个实验的数据更为准确
多进行几次实验。
5. 一个球从48米的高度自由落下,每次落地后反弹回原高度的一半,再落下。
(1)第几次落地之后反弹高度小于1米
(2)在第4次落地时共经过多少米
第1次反弹:48÷2=24(米)
第2次反弹:24÷2=12(米)
第3次反弹:12÷2=6(米)
第4次反弹:6÷2=3(米)
第5次反弹:3÷2=1.5(米)
第6次反弹:1.5÷2=0.75(米)
0.75<1,第六次落地之后反弹高度小于1米。
(1)第几次落地之后反弹高度小于1米
(2)在第4次落地时共经过多少米
48+24×2+12×2+6×2=132(米)
回顾观察记录的过程,你有什么体会?
要用发现的眼光、探索求知的精神对待日常生活中有趣的现象;在探索过程中,只有认真做实验,才可能
得到准确的数据,实验才有价值;实验的次数越多,
收集的数据越多,就越容易发现规律。
课堂小结
分数的意义和性质
综合与实践 球的反弹高度
苏教版五年级下册数学
通过实验收集数据、记录比较数据,能用分数表示球的反弹高度与下落高度的关系,进一步掌握求一个数是另一个数的几分之几的方法,加深对分数意义的理解。
经历操作实验、收集数据、计算比较等活动,感受用实验方法探究问题结论的过程,体会实验数据的重要性,积累基本活动经验,进一步发展数据分析观念。
学习目标
打篮球、踢足球、拍皮球等都是同学们喜爱的运动,大家有没有注意到这些球从高处落地后都会怎样?
球从高处落地后都会反弹。
课堂导入
通过上图中的活动,你想到了哪些问题?
如果把这些球,从同一高度自由落下,它们的反弹高度会一样吗?
如果同一个球,从不同的高度自由落下,反弹高度一样吗?
把它们从同一高度自由落下,哪种球反弹得高一些?
球的反弹高度和下落高度之间有什么关系?
选择一块靠墙的平地,在墙上量出一个高度并做上标记。再选择一个球从这个高度自由落下,在墙上标出球的反弹高度,量出结果并记录下来。
准备活动材料
一个皮球
卷尺
记录本
活动一 用皮球测反弹
活动内容:
组织活动
(1)确定投球、观察、测量和记录数据的同学。
(2)明确活动要求:①几次扔球的力度要一致,尽量让球自由落体;②观察和标记反弹高度的同学要认真,保持标记的位置尽量准确;③及时记录数据。
操作方法
(1)选一块靠墙的平地,在墙上量出三个不同的高度并做上标记。
(2)选择皮球从这三个不同的高度自由落下,在墙上标出球的反弹高度。
(3)量出结果并记录。
第一步:选择一块靠墙的平地,在墙上量出一个高度并做上标记。
第二步:让球的最下沿与墙上的高度标记齐平,松手,让球自由落下。
第三步:看清楚球的最下沿反弹的最高点,并迅速在墙上做上标记。
若看不清楚可以重复一次。
第四步:用尺子量出反弹高度并记录下来(测量结果取整厘米数,
以便于计算和比较)。
把球的上沿对齐墙上的刻度线,要看清球的反弹高度并迅速做好标记,测量要准确,记录的结果取整厘米数就可以了。
选择不同的高度做三次实验,记录量得的数据,并求出每次反弹的高度是下落高度的几分之几。
( )球 第一次 第二次 第三次
下落高度
反弹高度
反弹高度是下落高度的几分之几
皮
200厘米
240厘米
180厘米
80厘米
96厘米
72厘米
用同一个球做实验,你发现了什么?
球的反弹高度与下落的高度有关。
在同一个地点,同一个球从不同高度下落,其反弹高度是不一样的,但表示同一个球反弹高度与下落高度关系的分数大致不变,说明同一个球的弹性是一样的。
选择其他的球再做三次实验,记录实验的结果,并与同学交流。
( )球 第一次 第二次 第三次
下落高度
反弹高度
反弹高度是下落高度的几分之几
在小组内分享实验数据吧。
仍在刚才靠墙的平地,用排球和网球各做三次实验,记录实验的结果,并求出每次反弹的高度是下落高度的几分之几。
活动过程:
准备实验材料:
小组合作,通过实验标记、测量并记录实验结果,求出反弹高度是下落高度的几分之几。
网球
卷尺
记录本
羽毛球
( )球 第一次 第二次 第三次
下落高度
反弹高度
反弹高度是下落高度的几分之几
网
100厘米
120厘米
140厘米
50厘米
60厘米
70厘米
( )球 第一次 第二次 第三次
下落高度
反弹高度
反弹高度是下落高度的几分之几
排
100厘米
120厘米
140厘米
30厘米
36厘米
42厘米
用不同的球做实验,你发现了什么?
在同一个地点,不同的球从同一高度下落,其反弹高度一般不同,表示相应反弹高度与下落高度关系的分数也不同,说明不同的球的弹性是不一样的。
探究球的反弹高度与下落高度的关系时,要联系已学过的统计知识、测量方法以及本单元学过的分数知识;
日常生活中有很多有趣的数学问题,要善于用发现的眼光观察,并勇于探索;
解决一些实际问题时,需要认真实验才可能得到准确的数据和结论;
在实验中收集数据时,要注意准确操作、实事求是。收集的数据越多,越容易发现规律、获得结论。
通过这一次活动,你有什么收获?
同一种球的弹性主要取决于球内部所受到的压力,而压力的大小与球内充进的空气多少有关。在正式球类比赛时,对球的弹性都有明确的规定。例如,比赛用的篮球,从1.8米的高度自由落下后,第一次反弹的高度应大于1.2米、小于1.4米。
1. 填一填。
(1)同一个球从不同高度自由落地,反弹高度( 不同)。
(2)同一个球从不同高度下落,表示反弹高度与下落高度关系的分数大致( 相同 ),这说明同一个球的弹性是一样的。
不同
相同
(3)一个球从100米高度自由落下,每次落地后返弹回原高度的一半。反弹两次后,反弹的高度是100米的( )。
课堂练习
2. 一个球从50米高度自由落下,落地后反弹高度是24米,反弹高度是下落高度的几分之几
24÷50=
第一次 第二次 第三次
下落高度/厘米 200 240 180
反弹高度/厘米 80 96 72
反弹高度是下落高度的几分之几
(1)完成上表。 (2)通过计算比较,你发现了什么
(3)如果这个皮球从10米的高度落下,那么它第一次反弹的高度可能是多少米
(4)如果这个皮球落下后第一次反弹的高度是2米,那么这个皮球可能是从什么高度落下的
3. 下表是一个皮球从不同高度下落与反弹高度的测量记录。
(2)通过计算比较,你发现了什么
(3)如果这个皮球从10米的高度落下,那么它第一次反弹的高度可能是多少米
同一个球从不同高度下落,表示反弹高度与下落高度关系的分数相同。
10÷5×2=4(米)
(4)如果这个皮球落下后第一次反弹的高度是2米,那么这个皮球可能是从什么高度落下的
2÷2×5=5(米)
4. 在研究球的反弹高度的实验活动中,淘气让一个篮球从1.8米的高度自由落下。他一共做了5次实验,每次反弹的高度记录如下:(单位:米)
1.2 1.3 1.25 1.3 1.35
(1)这个篮球从1.8米的高度自由落下,平均每次的反弹高度是多少
(2)你觉得怎样可以让这个实验的数据更为准确
(1)这个篮球从1.8米的高度自由落下,平均每次的反弹高度是多少
(1.2+1.3+1.25+1.3+1.35)÷5=1.28(米)
(2)你觉得怎样可以让这个实验的数据更为准确
多进行几次实验。
5. 一个球从48米的高度自由落下,每次落地后反弹回原高度的一半,再落下。
(1)第几次落地之后反弹高度小于1米
(2)在第4次落地时共经过多少米
第1次反弹:48÷2=24(米)
第2次反弹:24÷2=12(米)
第3次反弹:12÷2=6(米)
第4次反弹:6÷2=3(米)
第5次反弹:3÷2=1.5(米)
第6次反弹:1.5÷2=0.75(米)
0.75<1,第六次落地之后反弹高度小于1米。
(1)第几次落地之后反弹高度小于1米
(2)在第4次落地时共经过多少米
48+24×2+12×2+6×2=132(米)
回顾观察记录的过程,你有什么体会?
要用发现的眼光、探索求知的精神对待日常生活中有趣的现象;在探索过程中,只有认真做实验,才可能
得到准确的数据,实验才有价值;实验的次数越多,
收集的数据越多,就越容易发现规律。
课堂小结
