4.3.1 等比数列的概念(第1课时) 课件(共22张PPT)
文档属性
| 名称 | 4.3.1 等比数列的概念(第1课时) 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-01 14:29:42 | ||
图片预览








文档简介
(共22张PPT)
4.3.1
等比数列的概念
第1课时
人教A版(2019)选择性必修第一册
学习目标
1.理解等比数列的含义.
2.掌握等比数列通项公式的推导过程及其运用.
3.理解等比数列与指数函数的关系.
4.核心素养:直观想象、数学运算、数学抽象
一、复习导入
等差数列:如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,通常用字母表示.
类比等差数列的研究思路和方法,从运算角度出发,我们还可以怎样研究数列?
二、新课讲授
1、等比数列的概念
问题:1.两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
, ,…, ; ①
, ,…, ; ②
, ,…, ③
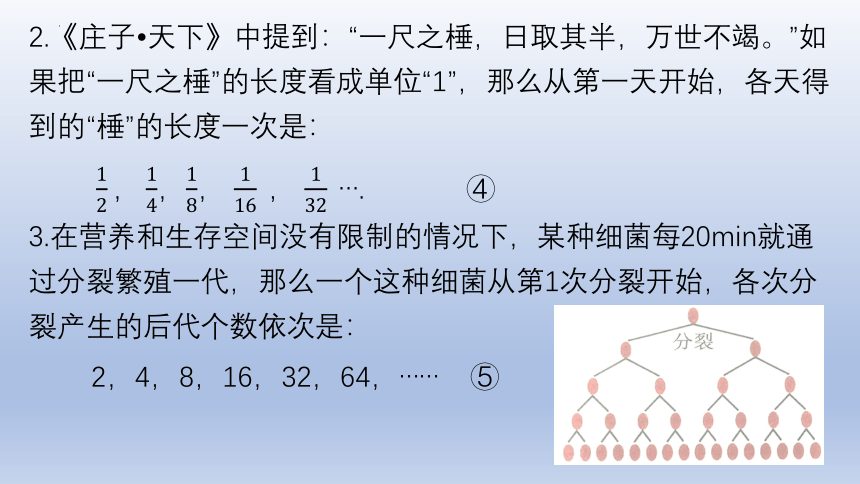
2.《庄子 天下》中提到:“一尺之棰,日取其半,万世不竭。”如果把“一尺之棰”的长度看成单位“1”,那么从第一天开始,各天得到的“棰”的长度一次是:
,, , …. ④
3.在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是:
2,4,8,16,32,64,…… ⑤
4.某人存入银行元,存期为五年,年利率为,那么按照复利,他五年内每年末得到的本利和分别是:
元,第一年末元;
复利是指把前一期的利息和本金加在一起算作本金,再计算下一期的利息
第二年末 元;
以此类推,可得:
, , ; ⑥
, ,…, ; ①
, ,…, ; ②
, ,…, ③
,, , …. ④
2,4,8,16,32,64,…… ⑤
, , ; ⑥
类比等差数列的研究,我们可以通过怎样的运算发现上述数列存在的规律?又是什么样的规律呢?
如果用表示数列①,那么有
,数列①有这样的取值规律:
, ,…, ; ①
,… .
第2项起,每一项与它的前一项的比都等于9.
其他数列的取值规律,并总结该规律.
, ,…, ; ②
, ,…, ③
,, , …. ④
2,4,8,16,32,64,…… ⑤
, , ; ⑥
第2项起,每一项与它的前一项的比都等于同一个常数.
等差数列 等比数列
一般地,如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,通常用字母表示.
一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,通常用字母表示.
等差数列 等比数列
:
= )
公差可正、可负、可为零.
公比的取值范围是什么?
追问1:由等比数列的定义,判断下列数列是不是等比数列.如果是,请写出它的公比.
(1)1,1.1,1.21,1.331,1.4641. ;
(2)0,,0, ;
(3)4,-8,16,-32,64,-128;
(4)5,5,5,5,5,5.
解:(1)设数列为 {},因为
所以,是等比数列,公比为1.1
(2)设数列为 {},因为无意义
所以,等比数列的首项不能为0
公比可以为0吗?
例如,0, ;
所以,公比不能为0
(3)设数列为 {},因为=-2
是等比数列,公比为-2
所以,公比可以是负数
(4)设数列为 {},因为=1
是等比数列,公比为1
非零常数列既是公差为0的等差数列,又是公比为1的等比数列.
等差数列 等比数列
= )
公差可正、可负、可为零.
公比的取值范围是什么?
可正、可负,不可为零
追问2:等差数列有等差中项,那么等比数列里也有相应的概念吗?又该如何定义它?
等差数列 等比数列
由三个数组成最简单的等差数列,这时, 叫做的等差中项,即.
由三个数组成等比数列,那么 叫做的等比中项,此时,.
问题2:你能根据等比数列的定义推导它的通项公式吗?
等差数列 等比数列
= + ,
= + ,
= + ,
归纳可得 = ,
当时,上式也成立.
因此,首项为,公差为的等差数列的通项公式为:
=
= ,
= ,
= ,
归纳可得 = ,
又 = =
因此,首项为,公比为的等比数列的通项公式为:
=
追问1:除了归纳法还有其他方法推导出等比数列的通项公式吗?
等差数列
→累加法
等比数列
→累乘法
等差数列 等比数列
=
= ,
=
左右两边分别依次相加,得到
所以 =
= ,……
左右两边分别依次相乘,得到
所以
3、等比数列与函数的关系
问题3:等差数列可以与一次函数建立联系,观察等比数列的通项公式,它与哪一类函数有关?
= ,
所以当>0且 ≠0时, ();
当()时, 即 =
指数型函数
(常数,)
构成一个等比数列{},其首项为,公比为
追问1:类比指数函数的性质,你能说说公比>0 的等比数列的单调性吗?
();
0<<1 >1 1
指数函数
等比数列
等比数列
单调递减
单调递增
单调递减
单调递增
>0
单调递减
单调递增
不变
<0
单调递增
单调递减
不变
三、巩固新知
例1 若等比数列{}的第4项和第6项分别为48和12,求{}的第5项.
例2 已知等比数列{}的公比,试用{}的第表示.
四、课堂小结
五、作业布置
课本P31:练习 第4、5题
等差数列 等比数列
常数
性质
通项公式
通项公式变形
公差
公差可正、可负、可为零
=
=
公差
公差可正、可负、不可为零
=
=
4.3.1
等比数列的概念
第1课时
人教A版(2019)选择性必修第一册
学习目标
1.理解等比数列的含义.
2.掌握等比数列通项公式的推导过程及其运用.
3.理解等比数列与指数函数的关系.
4.核心素养:直观想象、数学运算、数学抽象
一、复习导入
等差数列:如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,通常用字母表示.
类比等差数列的研究思路和方法,从运算角度出发,我们还可以怎样研究数列?
二、新课讲授
1、等比数列的概念
问题:1.两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
, ,…, ; ①
, ,…, ; ②
, ,…, ③
2.《庄子 天下》中提到:“一尺之棰,日取其半,万世不竭。”如果把“一尺之棰”的长度看成单位“1”,那么从第一天开始,各天得到的“棰”的长度一次是:
,, , …. ④
3.在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是:
2,4,8,16,32,64,…… ⑤
4.某人存入银行元,存期为五年,年利率为,那么按照复利,他五年内每年末得到的本利和分别是:
元,第一年末元;
复利是指把前一期的利息和本金加在一起算作本金,再计算下一期的利息
第二年末 元;
以此类推,可得:
, , ; ⑥
, ,…, ; ①
, ,…, ; ②
, ,…, ③
,, , …. ④
2,4,8,16,32,64,…… ⑤
, , ; ⑥
类比等差数列的研究,我们可以通过怎样的运算发现上述数列存在的规律?又是什么样的规律呢?
如果用表示数列①,那么有
,数列①有这样的取值规律:
, ,…, ; ①
,… .
第2项起,每一项与它的前一项的比都等于9.
其他数列的取值规律,并总结该规律.
, ,…, ; ②
, ,…, ③
,, , …. ④
2,4,8,16,32,64,…… ⑤
, , ; ⑥
第2项起,每一项与它的前一项的比都等于同一个常数.
等差数列 等比数列
一般地,如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,通常用字母表示.
一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,通常用字母表示.
等差数列 等比数列
:
= )
公差可正、可负、可为零.
公比的取值范围是什么?
追问1:由等比数列的定义,判断下列数列是不是等比数列.如果是,请写出它的公比.
(1)1,1.1,1.21,1.331,1.4641. ;
(2)0,,0, ;
(3)4,-8,16,-32,64,-128;
(4)5,5,5,5,5,5.
解:(1)设数列为 {},因为
所以,是等比数列,公比为1.1
(2)设数列为 {},因为无意义
所以,等比数列的首项不能为0
公比可以为0吗?
例如,0, ;
所以,公比不能为0
(3)设数列为 {},因为=-2
是等比数列,公比为-2
所以,公比可以是负数
(4)设数列为 {},因为=1
是等比数列,公比为1
非零常数列既是公差为0的等差数列,又是公比为1的等比数列.
等差数列 等比数列
= )
公差可正、可负、可为零.
公比的取值范围是什么?
可正、可负,不可为零
追问2:等差数列有等差中项,那么等比数列里也有相应的概念吗?又该如何定义它?
等差数列 等比数列
由三个数组成最简单的等差数列,这时, 叫做的等差中项,即.
由三个数组成等比数列,那么 叫做的等比中项,此时,.
问题2:你能根据等比数列的定义推导它的通项公式吗?
等差数列 等比数列
= + ,
= + ,
= + ,
归纳可得 = ,
当时,上式也成立.
因此,首项为,公差为的等差数列的通项公式为:
=
= ,
= ,
= ,
归纳可得 = ,
又 = =
因此,首项为,公比为的等比数列的通项公式为:
=
追问1:除了归纳法还有其他方法推导出等比数列的通项公式吗?
等差数列
→累加法
等比数列
→累乘法
等差数列 等比数列
=
= ,
=
左右两边分别依次相加,得到
所以 =
= ,……
左右两边分别依次相乘,得到
所以
3、等比数列与函数的关系
问题3:等差数列可以与一次函数建立联系,观察等比数列的通项公式,它与哪一类函数有关?
= ,
所以当>0且 ≠0时, ();
当()时, 即 =
指数型函数
(常数,)
构成一个等比数列{},其首项为,公比为
追问1:类比指数函数的性质,你能说说公比>0 的等比数列的单调性吗?
();
0<<1 >1 1
指数函数
等比数列
等比数列
单调递减
单调递增
单调递减
单调递增
>0
单调递减
单调递增
不变
<0
单调递增
单调递减
不变
三、巩固新知
例1 若等比数列{}的第4项和第6项分别为48和12,求{}的第5项.
例2 已知等比数列{}的公比,试用{}的第表示.
四、课堂小结
五、作业布置
课本P31:练习 第4、5题
等差数列 等比数列
常数
性质
通项公式
通项公式变形
公差
公差可正、可负、可为零
=
=
公差
公差可正、可负、不可为零
=
=
