人教版七年级数学上册第三章《一元一次方程》期末复习题 (3)(含答案)
文档属性
| 名称 | 人教版七年级数学上册第三章《一元一次方程》期末复习题 (3)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 24.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 10:25:45 | ||
图片预览


文档简介
第三章《一元一次方程》期末复习题
一、选择题
1.下列选项中,是一元一次方程的为( )
A. B. C.3+7=10 D.x +2x+1=0
2.如果3m=3n,那么下列等式不一定成立的是( )
A.m-3=n-3 B.3m+3=3n+2 C.5+m=5+n D.=
3.对于方程:,去分母后得到的方程是( )
A.2(5x-1)-12=3(1+ 2x) B.5x-1-6=3(1+2x)
C.2(5x-1)-6=3(1+2x) D.5x-1-2=1+2x
4.方程 移项正确的是( )
A. B. C. D.
5.王阿姨在甲批发市场以每件元的价格进了30件衬衫,又在乙批发市场以每件元的价格进了50件同样的衬衫.如果以每件元的价格将衬衫全部卖出,那么王阿姨( )
A.盈利了 B.亏损了
C.不盈也不亏 D.盈亏不能确定
6.某班级劳动时,将全班同学分成x个小组,若每小组11人,则余下1人;若每小组12人,则有一组少4人.按下列哪个选项重新分组,能使每组人数相同?( )
A.3组 B.5组 C.6组 D.7组
7.小明从家里骑自行车到学校,每小时骑15km,可早到10分钟,每小时骑12km就会迟到5分钟.问他家到学校的路程是多少km 设他家到学校的路程是xkm,则据题意列出的方程是( )
A.+=- B.-=+
C.-=- D.+10=-5
二、填空题
8.若 是关于 的方程 的解,则 ;
9.已知方程(a﹣2)x|a|﹣1+4=0是关于x的一元一次方程.则a的值为 ;
10.已知二元一次方程,用含x的代数式表示y,则 .
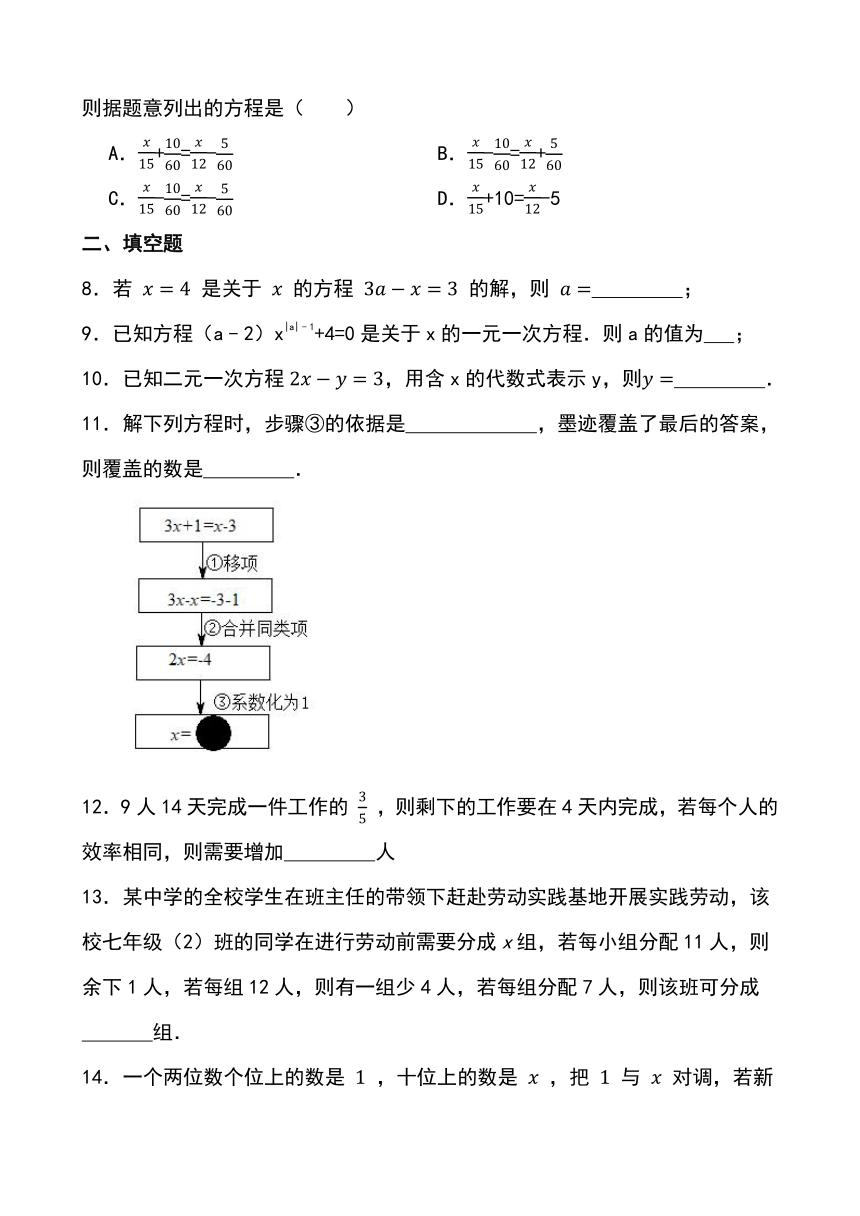
11.解下列方程时,步骤③的依据是 ,墨迹覆盖了最后的答案,则覆盖的数是 .
12.9人14天完成一件工作的 ,则剩下的工作要在4天内完成,若每个人的效率相同,则需要增加 人
13.某中学的全校学生在班主任的带领下赶赴劳动实践基地开展实践劳动,该校七年级(2)班的同学在进行劳动前需要分成x组,若每小组分配11人,则余下1人,若每组12人,则有一组少4人,若每组分配7人,则该班可分成
组.
14.一个两位数个位上的数是 ,十位上的数是 ,把 与 对调,若新两位数比原两位数小 ,则x的值为
15.某市为了鼓励居民节约用水,对自来水用户按如下标准收费,若每月每户用水不超过15吨,按每吨1元收费,若超过15吨,则超过部分每吨按2元收费.如果小明家12月份交纳的水费29元,则小明家这个月实际用水 吨.
16.明代数学家吴敬所著的《九章自述比类大全》中有一首数学诗叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增,共灯三百八十一,请问顶层几盏灯?”大致意思是有一座七层高塔,从底层开始,每层安装的灯的数目都是上一层的2倍,请你算出塔的顶层有 盏灯.
三、解答题
17.解一元一次方程:
(1) ;
(2) .
18.方程-m=5(y-m)与方程4y-7=1+2y的解相同,求2m+1的值.
19.方程2﹣3(x+1)=0的解与关于x的方程 的解互为倒数,求k的值.
20.将一装满水的直径为40cm、高为60cm的圆柱形水桶里的水全部灌入另一个半径为30cm的圆柱形水桶里,问这时水的高度是多少?
21.某校班级篮球联赛中,每场比赛都要分胜负,每队胜1场得3分,负1场得1分,如果某班在第一轮的28场比赛中得48分,那么这个班胜了多少场?
22.这个星期周末,七年级准备组织观看电影《我和我的祖国》,由各班班长负责买票,每班人数都多于50人,票价每张20元,一班班长问售票员买团体票是否可以优惠,售票员说:50人以上的团体票有两个优惠方案可选择:
方案一:全体人员可打8折;方案2:若打9折,有7人可以免票.
(1)2班有61名学生,他该选择哪个方案?
(2)一班班长思考一会儿说我们班无论选择哪种方案要付的钱是一样的,问你知道一班有几人吗?
答案解析部分
1.A
2.B
3.A
4.C
5.A
6.D
7.A
8.
9.-2
10.
11.等式两边同时除以一个不为0的数,等式仍然成立;-2
12.12
13.8
14.3
15.22
16.3
17.(1)解:
去括号得, ,
移项合并得, ,
系数化为1,得: .
(2)解:
去分母得,
去括号得, ,
移项合并得, ,
系数化为1,得: .
18.解:∵4y-7=1+2y,
∴解得y=4.
∵方程 与方程4y-7=1+2y的解相同,
∴,
∴,即
解得
∴2m+1=10.
19.解:2﹣3(x+1)=0的解为x= ,
则 的解为x=﹣3,代入得 ﹣3k﹣2=﹣6,
解得:k=1.故答案为:1
20.解:设这时水的高度是xcm,
由题意得:202π 60=302π x,
解得:x= ,
答:这时水的高度是 cm
21.解:设这个班胜了x场,则负(28﹣x)场,根据题意得:3x+(28﹣x)=48,解得:x=10.答:这个班胜了10场
22.解:(Ⅰ)∵方案一:61×20×0.8=976(元),
方案二:(61﹣7)×0.9×20=972(元),
∴选择方案二.
(Ⅱ)假设1班有x人,根据题意得出:
x×20×0.8=(x﹣7)×0.9×20,
解得:x=63,
答:1班有63人.
一、选择题
1.下列选项中,是一元一次方程的为( )
A. B. C.3+7=10 D.x +2x+1=0
2.如果3m=3n,那么下列等式不一定成立的是( )
A.m-3=n-3 B.3m+3=3n+2 C.5+m=5+n D.=
3.对于方程:,去分母后得到的方程是( )
A.2(5x-1)-12=3(1+ 2x) B.5x-1-6=3(1+2x)
C.2(5x-1)-6=3(1+2x) D.5x-1-2=1+2x
4.方程 移项正确的是( )
A. B. C. D.
5.王阿姨在甲批发市场以每件元的价格进了30件衬衫,又在乙批发市场以每件元的价格进了50件同样的衬衫.如果以每件元的价格将衬衫全部卖出,那么王阿姨( )
A.盈利了 B.亏损了
C.不盈也不亏 D.盈亏不能确定
6.某班级劳动时,将全班同学分成x个小组,若每小组11人,则余下1人;若每小组12人,则有一组少4人.按下列哪个选项重新分组,能使每组人数相同?( )
A.3组 B.5组 C.6组 D.7组
7.小明从家里骑自行车到学校,每小时骑15km,可早到10分钟,每小时骑12km就会迟到5分钟.问他家到学校的路程是多少km 设他家到学校的路程是xkm,则据题意列出的方程是( )
A.+=- B.-=+
C.-=- D.+10=-5
二、填空题
8.若 是关于 的方程 的解,则 ;
9.已知方程(a﹣2)x|a|﹣1+4=0是关于x的一元一次方程.则a的值为 ;
10.已知二元一次方程,用含x的代数式表示y,则 .
11.解下列方程时,步骤③的依据是 ,墨迹覆盖了最后的答案,则覆盖的数是 .
12.9人14天完成一件工作的 ,则剩下的工作要在4天内完成,若每个人的效率相同,则需要增加 人
13.某中学的全校学生在班主任的带领下赶赴劳动实践基地开展实践劳动,该校七年级(2)班的同学在进行劳动前需要分成x组,若每小组分配11人,则余下1人,若每组12人,则有一组少4人,若每组分配7人,则该班可分成
组.
14.一个两位数个位上的数是 ,十位上的数是 ,把 与 对调,若新两位数比原两位数小 ,则x的值为
15.某市为了鼓励居民节约用水,对自来水用户按如下标准收费,若每月每户用水不超过15吨,按每吨1元收费,若超过15吨,则超过部分每吨按2元收费.如果小明家12月份交纳的水费29元,则小明家这个月实际用水 吨.
16.明代数学家吴敬所著的《九章自述比类大全》中有一首数学诗叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增,共灯三百八十一,请问顶层几盏灯?”大致意思是有一座七层高塔,从底层开始,每层安装的灯的数目都是上一层的2倍,请你算出塔的顶层有 盏灯.
三、解答题
17.解一元一次方程:
(1) ;
(2) .
18.方程-m=5(y-m)与方程4y-7=1+2y的解相同,求2m+1的值.
19.方程2﹣3(x+1)=0的解与关于x的方程 的解互为倒数,求k的值.
20.将一装满水的直径为40cm、高为60cm的圆柱形水桶里的水全部灌入另一个半径为30cm的圆柱形水桶里,问这时水的高度是多少?
21.某校班级篮球联赛中,每场比赛都要分胜负,每队胜1场得3分,负1场得1分,如果某班在第一轮的28场比赛中得48分,那么这个班胜了多少场?
22.这个星期周末,七年级准备组织观看电影《我和我的祖国》,由各班班长负责买票,每班人数都多于50人,票价每张20元,一班班长问售票员买团体票是否可以优惠,售票员说:50人以上的团体票有两个优惠方案可选择:
方案一:全体人员可打8折;方案2:若打9折,有7人可以免票.
(1)2班有61名学生,他该选择哪个方案?
(2)一班班长思考一会儿说我们班无论选择哪种方案要付的钱是一样的,问你知道一班有几人吗?
答案解析部分
1.A
2.B
3.A
4.C
5.A
6.D
7.A
8.
9.-2
10.
11.等式两边同时除以一个不为0的数,等式仍然成立;-2
12.12
13.8
14.3
15.22
16.3
17.(1)解:
去括号得, ,
移项合并得, ,
系数化为1,得: .
(2)解:
去分母得,
去括号得, ,
移项合并得, ,
系数化为1,得: .
18.解:∵4y-7=1+2y,
∴解得y=4.
∵方程 与方程4y-7=1+2y的解相同,
∴,
∴,即
解得
∴2m+1=10.
19.解:2﹣3(x+1)=0的解为x= ,
则 的解为x=﹣3,代入得 ﹣3k﹣2=﹣6,
解得:k=1.故答案为:1
20.解:设这时水的高度是xcm,
由题意得:202π 60=302π x,
解得:x= ,
答:这时水的高度是 cm
21.解:设这个班胜了x场,则负(28﹣x)场,根据题意得:3x+(28﹣x)=48,解得:x=10.答:这个班胜了10场
22.解:(Ⅰ)∵方案一:61×20×0.8=976(元),
方案二:(61﹣7)×0.9×20=972(元),
∴选择方案二.
(Ⅱ)假设1班有x人,根据题意得出:
x×20×0.8=(x﹣7)×0.9×20,
解得:x=63,
答:1班有63人.
