2023-2024学年苏科版数学九年级上册期末综合培优检测试题(含答案)
文档属性
| 名称 | 2023-2024学年苏科版数学九年级上册期末综合培优检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 391.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 11:14:58 | ||
图片预览




文档简介
2023-2024学年苏科版数学
九年级上册期末综合培优检测试题
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,选出符合题目要求的一项。
1.已知关于的一元二次方程的一个根是,则的值为( )
A. B. C. 或 D.
2.用配方法解一元二次方程,下面配方正确的是( )
A. B. C. D.
3.已知一元二次方程的两根为,,则的值为( )
A. B. C. D.
4.若实数,分别满足方程,,则的值为( )
A. B. C. 或 D. 或
5.在一次酒会上,每两人都只碰一次杯,如果一共碰杯次,则参加酒会的人数为( )
A. 人 B. 人 C. 人 D. 人
6.的半径是,弦,,,则弦与的距离是( )
A. B. C. 或 D. 或
7.如图,四边形内接于,是的直径,,则的度数是( )
A. B. C. D.
8.若圆锥的底面半径为,母线长为,则它的侧面展开图的圆心角为( )
A. B. C. D.
9.在战“疫”诗歌创作大赛中,有名同学进入了决赛,他们的最终成绩均不同.小弘同学想知道自己能否进入前名,除要了解自己的成绩外,还要了解这名同学成绩的( )
A. 中位数 B. 平均数 C. 众数 D. 方差
10.正方形的边长为,以各边为直径在正方形内画半圆,得到如图所示的阴影部分.若随机向正方形内投一粒米,则米粒落在阴影部分的概率为( )
A. B. C. D.
11.如图,设边长为的等边三角形的高、内切圆的半径、外接圆的半径分别为、、,则下列结论不正确的是( )
A. B. C. D.
12.如图,点,的坐标分别为,,点为坐标平面内一点,,点为线段的中点,连接,则长的最大值为( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
13.已知关于的方程有实数根,则的取值范围是 .
14.如图,为的直径,弦于点,已知,,则的半径为 .
15.如右上图,的顶点均在上,,,则的半径为______ .
16.已知一组数据、、、的方差是,则新的一组数据、、、为常数,的方差是 用含、的代数式表示.
17.某农场的粮食产量在两年内从增加到,且第一年的增长率是第二年的两倍.如果设第二年的增长率为,则可列方程为 .
三、解答题:本题共8小题,共69分。解答应写出文字说明,证明过程或演算步骤。
18.(6分)解方程:
;
.
19.本小题分
已知关于的方程.
求证:无论取何实数,方程总有实数根;
若方程有两个不等实根,,且满足,求的值.
20.本小题分
如图,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图是一款拱门的示意图,其中为中点,为拱门最高点,线段经过圆心,已知拱门的半径为,拱门最下端.
求拱门最高点到地面的距离;
现需要给房间内搬进一个长和宽为,高为的桌子,已知搬桌子的两名工人在搬运时所抬高度相同,且高度为,判断搬运该桌子时是否能够通过拱门.参考数据:
21.本小题分
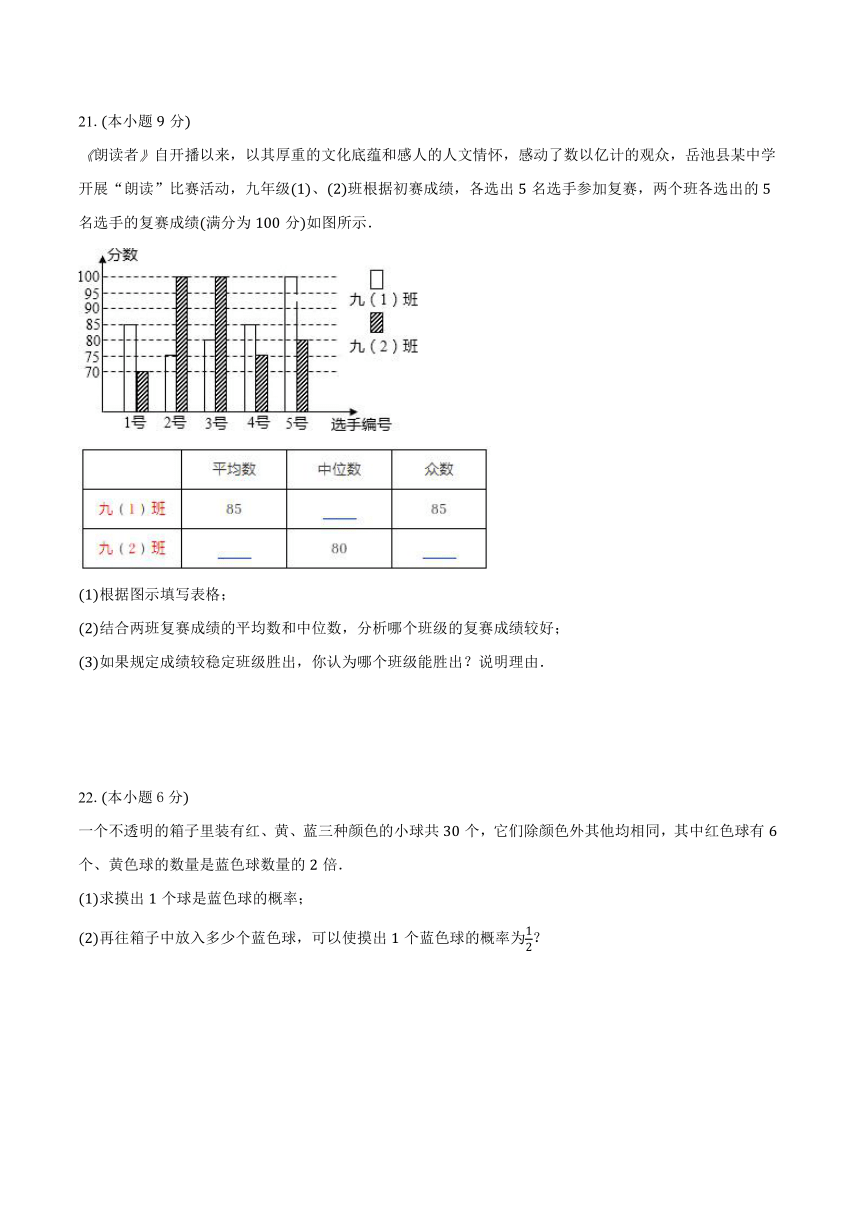
朗读者自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级、班根据初赛成绩,各选出名选手参加复赛,两个班各选出的名选手的复赛成绩满分为分如图所示.
根据图示填写表格;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
22.本小题6分
一个不透明的箱子里装有红、黄、蓝三种颜色的小球共个,它们除颜色外其他均相同,其中红色球有个、黄色球的数量是蓝色球数量的倍.
求摸出个球是蓝色球的概率;
再往箱子中放入多少个蓝色球,可以使摸出个蓝色球的概率为?
23.本小题分
水果店张阿姨以每千克元的价格购进某种水果若干千克,然后以每千克元的价格出售,每天售出千克.通过调查发现,这种水果每千克的售价每降低元,每天可多售出千克,为了保证每天至少售出千克,张阿姨决定降价销售.
若售价降低元,则每天的销售量为______千克、销售利润为______元;
若将这种水果每千克降价元,则每天的销售量是______千克用含的代数式表示;
销售这种水果要想每天盈利元,张阿姨应将每千克的销售价降至多少元?
24.本小题0分
如图,内接于,且直线过点,且与直径的延长线交于点,,垂足为,平分,,垂足为.
求证:直线是的切线;
若,求图中阴影部分的面积.
25.本小题分
如图,在四边形中,,,.
,点从点出发,以每秒的速度沿折线方向运动,点从点出发,以每秒的速度沿线段方向向点运动已知动点,同时出发,当点运动到点时,运动停止,设运动时间为.
直接写出的长
当四边形为平行四边形时,直接写出四边形的周长
在点、点的运动过程中,是否存在某一时刻,使得的面积为若存在,请求出所有满足条件的的值若不存在,请说明理由.
九年级上册期末综合培优检测试题答案
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18. 解:,
,
,
,;
,
,
,
,,
,.
19. 解:,
,
,
无论取何实数,方程总有实数根;
根据题意得,,,
,
,
,
,
,
,
,,
,
的值为.
20. 解:如图中,连接.
,经过圆心,
,
,
,
拱门最高点到地面的距离为
如图,弦,且,连接.
,经过圆心,
,
,
,
,
运该桌子时能够通过拱门.
21. 解:九班位同学的成绩为:、、、、,
其中位数为分;
九班位同学的成绩为:、、、、,
九班的平均数为分,其众数为分,
补全表格如下:
九班成绩好些,
两个班的平均数都相同,而九班的中位数高,
在平均数相同的情况下,中位数高的九班成绩好些;
九班的成绩更稳定,能胜出.
,
,
,
九班的成绩更稳定,能胜出.
22. 【小题】
解:蓝色球有个,
所以摸出一个球是蓝色球;
【小题】
设再往箱子里放入个蓝色球,可以使摸出个蓝色球的概率为,
则,
解得,.
答:再往箱子里放入个蓝色球,可以使摸出的个蓝色球的概率为.
23. 解:;.
.
设这种水果每千克降价元,
根据题意得:,
,
解得:或,
当时,销售量是;
当时,销售量是.
每天至少售出千克,
.
,
答:张阿姨应将每千克的销售价降至元.
24. 证明:如图,连接,
,
,
平分,
,
,
,
,
,
为半径,
直线是的切线;
解:如图,连接,则.
是圆的直径,
又,
,
,
在中,,,
,
设,则,,
解得:,
.
在中,,,
得.
在中,.
.
25. 解:;
;
当点在线段上时,即:时,
如图,
,
;
当点在线段上时,即:时,
如图,
,,
,
或舍,
即:满足条件的的值为秒或秒.
九年级上册期末综合培优检测试题
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,选出符合题目要求的一项。
1.已知关于的一元二次方程的一个根是,则的值为( )
A. B. C. 或 D.
2.用配方法解一元二次方程,下面配方正确的是( )
A. B. C. D.
3.已知一元二次方程的两根为,,则的值为( )
A. B. C. D.
4.若实数,分别满足方程,,则的值为( )
A. B. C. 或 D. 或
5.在一次酒会上,每两人都只碰一次杯,如果一共碰杯次,则参加酒会的人数为( )
A. 人 B. 人 C. 人 D. 人
6.的半径是,弦,,,则弦与的距离是( )
A. B. C. 或 D. 或
7.如图,四边形内接于,是的直径,,则的度数是( )
A. B. C. D.
8.若圆锥的底面半径为,母线长为,则它的侧面展开图的圆心角为( )
A. B. C. D.
9.在战“疫”诗歌创作大赛中,有名同学进入了决赛,他们的最终成绩均不同.小弘同学想知道自己能否进入前名,除要了解自己的成绩外,还要了解这名同学成绩的( )
A. 中位数 B. 平均数 C. 众数 D. 方差
10.正方形的边长为,以各边为直径在正方形内画半圆,得到如图所示的阴影部分.若随机向正方形内投一粒米,则米粒落在阴影部分的概率为( )
A. B. C. D.
11.如图,设边长为的等边三角形的高、内切圆的半径、外接圆的半径分别为、、,则下列结论不正确的是( )
A. B. C. D.
12.如图,点,的坐标分别为,,点为坐标平面内一点,,点为线段的中点,连接,则长的最大值为( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
13.已知关于的方程有实数根,则的取值范围是 .
14.如图,为的直径,弦于点,已知,,则的半径为 .
15.如右上图,的顶点均在上,,,则的半径为______ .
16.已知一组数据、、、的方差是,则新的一组数据、、、为常数,的方差是 用含、的代数式表示.
17.某农场的粮食产量在两年内从增加到,且第一年的增长率是第二年的两倍.如果设第二年的增长率为,则可列方程为 .
三、解答题:本题共8小题,共69分。解答应写出文字说明,证明过程或演算步骤。
18.(6分)解方程:
;
.
19.本小题分
已知关于的方程.
求证:无论取何实数,方程总有实数根;
若方程有两个不等实根,,且满足,求的值.
20.本小题分
如图,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图是一款拱门的示意图,其中为中点,为拱门最高点,线段经过圆心,已知拱门的半径为,拱门最下端.
求拱门最高点到地面的距离;
现需要给房间内搬进一个长和宽为,高为的桌子,已知搬桌子的两名工人在搬运时所抬高度相同,且高度为,判断搬运该桌子时是否能够通过拱门.参考数据:
21.本小题分
朗读者自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级、班根据初赛成绩,各选出名选手参加复赛,两个班各选出的名选手的复赛成绩满分为分如图所示.
根据图示填写表格;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
22.本小题6分
一个不透明的箱子里装有红、黄、蓝三种颜色的小球共个,它们除颜色外其他均相同,其中红色球有个、黄色球的数量是蓝色球数量的倍.
求摸出个球是蓝色球的概率;
再往箱子中放入多少个蓝色球,可以使摸出个蓝色球的概率为?
23.本小题分
水果店张阿姨以每千克元的价格购进某种水果若干千克,然后以每千克元的价格出售,每天售出千克.通过调查发现,这种水果每千克的售价每降低元,每天可多售出千克,为了保证每天至少售出千克,张阿姨决定降价销售.
若售价降低元,则每天的销售量为______千克、销售利润为______元;
若将这种水果每千克降价元,则每天的销售量是______千克用含的代数式表示;
销售这种水果要想每天盈利元,张阿姨应将每千克的销售价降至多少元?
24.本小题0分
如图,内接于,且直线过点,且与直径的延长线交于点,,垂足为,平分,,垂足为.
求证:直线是的切线;
若,求图中阴影部分的面积.
25.本小题分
如图,在四边形中,,,.
,点从点出发,以每秒的速度沿折线方向运动,点从点出发,以每秒的速度沿线段方向向点运动已知动点,同时出发,当点运动到点时,运动停止,设运动时间为.
直接写出的长
当四边形为平行四边形时,直接写出四边形的周长
在点、点的运动过程中,是否存在某一时刻,使得的面积为若存在,请求出所有满足条件的的值若不存在,请说明理由.
九年级上册期末综合培优检测试题答案
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
13.
14.
15.
16.
17.
18. 解:,
,
,
,;
,
,
,
,,
,.
19. 解:,
,
,
无论取何实数,方程总有实数根;
根据题意得,,,
,
,
,
,
,
,
,,
,
的值为.
20. 解:如图中,连接.
,经过圆心,
,
,
,
拱门最高点到地面的距离为
如图,弦,且,连接.
,经过圆心,
,
,
,
,
运该桌子时能够通过拱门.
21. 解:九班位同学的成绩为:、、、、,
其中位数为分;
九班位同学的成绩为:、、、、,
九班的平均数为分,其众数为分,
补全表格如下:
九班成绩好些,
两个班的平均数都相同,而九班的中位数高,
在平均数相同的情况下,中位数高的九班成绩好些;
九班的成绩更稳定,能胜出.
,
,
,
九班的成绩更稳定,能胜出.
22. 【小题】
解:蓝色球有个,
所以摸出一个球是蓝色球;
【小题】
设再往箱子里放入个蓝色球,可以使摸出个蓝色球的概率为,
则,
解得,.
答:再往箱子里放入个蓝色球,可以使摸出的个蓝色球的概率为.
23. 解:;.
.
设这种水果每千克降价元,
根据题意得:,
,
解得:或,
当时,销售量是;
当时,销售量是.
每天至少售出千克,
.
,
答:张阿姨应将每千克的销售价降至元.
24. 证明:如图,连接,
,
,
平分,
,
,
,
,
,
为半径,
直线是的切线;
解:如图,连接,则.
是圆的直径,
又,
,
,
在中,,,
,
设,则,,
解得:,
.
在中,,,
得.
在中,.
.
25. 解:;
;
当点在线段上时,即:时,
如图,
,
;
当点在线段上时,即:时,
如图,
,,
,
或舍,
即:满足条件的的值为秒或秒.
同课章节目录
