第2章对称图形——圆 单元达标测试卷 2023--2024学年苏科版九年级数学上册(含解析)
文档属性
| 名称 | 第2章对称图形——圆 单元达标测试卷 2023--2024学年苏科版九年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 373.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 11:16:19 | ||
图片预览




文档简介
苏科版九年级数学上册第2章对称图形——圆单元达标测试卷
一、单选题
1.已知⊙O的半径为4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
2.若的半径为5,点到圆心的距离为,当点在圆上时,则有( ).
A. B. C. D.
3.一个圆锥的底面半径为 ,母线长为 ,这个圆锥的侧面积为( )
A. B. C. D.
4.若扇形的半径为4,圆心角为90°,则此扇形的弧长是( )
A.π B.2π C.4π D.8π
5.已知⊙O的半径为5cm,若OP=3cm,则点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O上 C.点P在⊙O内 D.不能确定
6.给出下列命题:①反比例函数的图象经过一、三象限,且y随x的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(右图);④相等的弧所对的圆周角相等.其中正确的是( )
A.③④ B.①②③ C.②④ D.①②③④
7.如图,在平面直角坐标系中,点爿是双曲线y= 上的一点,以点爿为圆心,0A为半径画圆。交两坐标轴于点B,C.若OB=8,则OC的长为( )
A.2 B.4 C.2 D.6
8.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=20°,则∠D等于( )
A.20° B.30° C.50° D.40°
9.如图,A、B、C是⊙O上的三点,已知 ,则 ( )
A.15° B. C. D.
10.如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知 和 所对的圆心角分别为90°和50°,则∠P=( )
A.45° B.40° C.25° D.20°
二、填空题
11.如图,扇形纸叠扇完全打开后,扇形ABC的面积为300πcm2,∠BAC=120°,BD=2AD,则BD的长度为 cm.
12.如图,为半圆内一点,为圆心,直径长为,,,将绕圆心逆时针旋转至,点在上,则边扫过区域图中阴影部分的面积为 结果保留
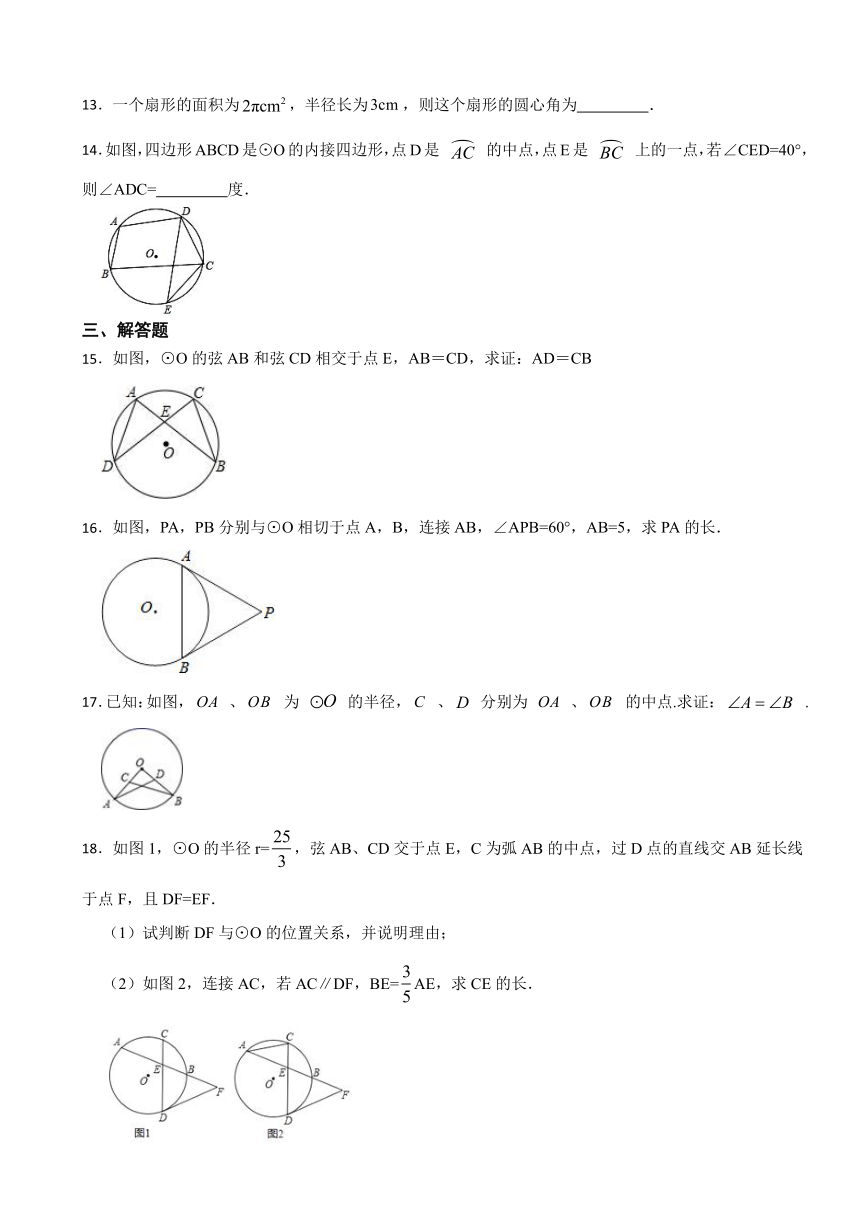
13.一个扇形的面积为,半径长为,则这个扇形的圆心角为 .
14.如图,四边形ABCD是⊙O的内接四边形,点D是 的中点,点E是 上的一点,若∠CED=40°,则∠ADC= 度.
三、解答题
15.如图,⊙O的弦AB和弦CD相交于点E,AB=CD,求证:AD=CB
16.如图,PA,PB分别与⊙O相切于点A,B,连接AB,∠APB=60°,AB=5,求PA的长.
17.已知:如图, 、 为 的半径, 、 分别为 、 的中点.求证: .
18.如图1,⊙O的半径r=,弦AB、CD交于点E,C为弧AB的中点,过D点的直线交AB延长线于点F,且DF=EF.
(1)试判断DF与⊙O的位置关系,并说明理由;
(2)如图2,连接AC,若AC∥DF,BE=AE,求CE的长.
四、综合题
19.如图,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧BC上一点,连结BD,AD,OC,∠ADB=30°.
(1)求∠AOC的度数;
(2)若弦BC=6 cm,求图中劣弧BC的长.
20.如图,AB=AC,⊙O为△ABC的外接圆,AF为⊙O的直径,四边形ABCD是平行四边形.
(1)求证:AD是⊙O的切线;
(2)若∠BAC=45°,AF=2,求阴影部分的面积.
21.已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.
(1)求扇形OBC的面积(结果保留π);
(2)求证:CD是⊙O的切线.
22.如图:
(1)实践操作:如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.
(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点O.
②以O为圆心,OC为半径作圆.
(2)综合运用:在你所作的图中,直线AB与⊙O存在怎样的位置关系,请说明理由.
(3)若AC=6,BC=8,则⊙O的半径为 .
23.如图,AC是⊙O的直径,AD是⊙O的弦,过点C作CB⊥AC交AD的延长线于点B,点E为BC的中点,连接DE、DC.
(1)求证:ED=EC.
(2)求证:DE是⊙O的切线.
(3)若OA= DB,求tanB的值.
答案解析部分
1.【答案】A
【解析】【分析】设圆的半径为R,圆心到直线的距离为d:当dR时,直线与圆相离。
∵3<4
∴直线l与⊙O的位置关系是相交.
故选A.
【点评】本题属于基础应用题,只需学生熟练掌握直线与圆的位置关系,即可完成。
2.【答案】C
【解析】【解答】解: 若的半径为5,点P到圆心的距离为d,当点P在圆上时,则有d=5.
故答案为:C.
【分析】 如果用r表示圆的半径,d表示同一平面内一点到圆心的距离,则 d>r 点在圆外, d=r 点在圆上 d<r 点在圆内,据此可得答案.
3.【答案】B
【解析】【解答】解:这个圆锥的侧面积=π×3×5=15πcm2,
故答案为:B.
【分析】圆锥侧面积公式S=πrl代入即可,其中r为圆锥的底面半径 ,l为母线长.
4.【答案】B
【解析】【分析】扇形的弧长=,把相应数值代入即可求解.
扇形的弧长=,
故选B.
5.【答案】C
【解析】【解答】解:∵点P到圆心的距离d=3<5=r,
∴该点P在⊙O内.
故答案为:C.
【分析】根据点到圆心的距离和圆的半径之间的数量关系,即可判断点和圆的位置关系,由题知点P到圆心的距离小于半径,可得出点P在⊙O内.
6.【答案】A
【解析】【分析】分别根据反比例函数的性质、矩形的性质及勾股定理、圆心角、弧、弦的关系对每小题进行逐一解答.
【解答】①反比例函数y= 的图象的图象两个分支分别位于一、三象限,而不是经过一、三象限,故此小题错误;
②两条对角线互相平分且有一个角是直角的四边形是矩形,对角线相等且有一个内角是直角的四边形有可能是梯形,故此小题错误;
③符合勾股定理的历史,故此小题正确;
④符合圆心角、弧、弦的关系,故此小题正确.
所以③④正确.
故选A.
7.【答案】B
【解析】【解答】解:过点A作AD⊥OB于点D,连接CB
∵∠COB=90°
∴BC是直径,点C、B、A在同一条直线上,
∵OB=8
∴OD=OB=4
当x=4时,y=8÷4=2
∴点A(4,2)
设yAB=kx+b
由题意得:
解之:
∴yAB=x+4
当x=0时,则y=4
∴点C(0,4)
∴OC=4
故答案为:B
【分析】过点A作AD⊥OB于点D,连接CB,利用圆周角定理可证得BC是直径,点C、B、A在同一条直线上,再利用垂径定理求出OD的长,就可得到点A的横坐标,利用函数解析式求出点A的纵坐标,就可得到点A的坐标,然后利用待定系数法求出直线AB的函数解析式,就可求出直线AB与y轴的交点C的坐标,从而可求出OC的长。
8.【答案】C
【解析】【解答】解:连接OC,
∵DC切⊙O于点C,
∴∠OCD=90°,
∵∠A=20°,
∴∠OCA=20°,
∴∠DOC=40°,
∴∠D=90°-40°=50°.
故答案为:C.
【分析】连接OC,根据切线的性质可得∠OCD=90°,根据等腰三角形的性质可得∠A=∠OCA=20°,结合外角的性质可得∠DOC=40°,然后根据余角的性质进行计算.
9.【答案】D
【解析】【解答】∵∠O=60°,
∴∠C=∠O=×60°=30°,
故答案为:D.
【分析】根据同弧所对的圆周角等于圆心角的一半.即可得出答案.
10.【答案】D
【解析】【解答】解:∵ 和 所对的圆心角分别为90°和50°,
∴∠A=25°,∠ADB=45°,
∵∠P+∠A=∠ADB,
∴∠P=∠ADB﹣∠P=45°﹣25°=20°.
故选D.
【分析】先由圆周角定理求出∠A与∠ADB的度数,然后根据三角形外角的性质即可求出∠P的度数.
11.【答案】20
【解析】【解答】解:设AD=x,则AB=3x.
由题意300π= ,
解得x=10,
∴BD=2x=20cm.
故答案为20.
【分析】根据BD=2AD可设AD=x,则AB=3x,由扇形的面积=可求出x的值,则BD的长度可求。
12.【答案】
【解析】【解答】解:∵,将绕圆心逆时针旋转至,
∴∠B'OC'=60°,△BOC≌△B'OC',
∴∠B'OC=180°-60°-60°=60°,
∴∠C'B'O=90°-60°=30°,∠B'OB=∠BOC+∠B'OC=120°,
∵AB=2cm,
∴OB=1cm,OC'=cm,
∴,
∴,,
∴,
故答案为:.
【分析】根据旋转的性质求出∠B'OC'=60°,△BOC≌△B'OC',再利用全等三角形的性质以及扇形面积公式等计算求解即可。
13.【答案】80°
【解析】【解答】解:扇形所在圆的面积为: ,
扇形的圆心角度数为: ,
故答案为:80°.
【分析】先求出整圆的面积,再求出扇形的面积占整圆面积的百分比,最后乘以360°即可得到答案。
14.【答案】100
【解析】【解答】解:如图,
连接AE,
∵点D是 的中点,
∴∠AED=∠CED,
∵∠CED=40°,
∴∠AEC=2∠CED=80°,
∵四边形ADCE是圆内接四边形,
∴∠ADC+∠AEC=180°,
∴∠ADC=180°﹣∠AEC=100°,
故答案为:100.
【分析】连接AE,先求得∠CED,再求得∠AEC,最后根据圆内接四边形对角互补求得∠ADC即可。
15.【答案】证明:∵AB=CD
∴
∴
∴ =
∴AD=BC.
【解析】【分析】由圆心角、弦、弧之间的关系定理可得和弧的构成可求解.
16.【答案】解:∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,
∴AB=PA=5
【解析】【分析】由切线长定理可得PA=PB,由∠APB=60°可得△PAB是等边三角形,从而得出答案.
17.【答案】证明:∵ , 为 的半径, , 分别为 , 的中点,
∴ ,
.
在 与 中,
∵ ,
∴ .
∴ .
【解析】【分析】先利用边角边定理证明△AOD≌△BOC,则由全等三角形的性质即可得出∠A=∠B.
18.【答案】证明:(1)如图1,连接OC、OD;∵C为弧AB的中点,∴OC⊥AB,∠OCE+∠AEC=90°;∴DF=EF,∴∠FDE=∠FED=∠AEC;∵OA=OC,∴∠OCE=∠ODC,∴∠ODC+∠CDF=90°,即OD⊥DF,∴DF与⊙O相切.(2)如图2,连接OA、OC;由(1)知OC⊥AB,∴AH=BH;∵AC∥DF,∴∠ACD=∠CDF;而EF=DF,∴∠DEF=∠CDF=∠ACD,∴AC=AE;设AE=5λ,则BE=3λ,∴AH=4λ,HE=λ,AC=AE=5λ;∴由勾股定理得:CH=3λ;CE2=CH2+HE2=9λ2+λ2,∴CE=λ;在直角△AOH中,由勾股定理得:AO2=AH2+OH2,即r2=(r﹣3λ)2+(4λ)2,解得:λ=r=x=2,∴CE=2.
【解析】【分析】(1)如图,作辅助线;证明∠ODC+∠CDF=90°,即可解决问题.
(2)如图,作辅助线;证明OH⊥AB,AH=4λ,此为解题的关键性结论;证明CE=λ;列出方程r2=(r﹣3λ)2+(4λ)2,求出λ=r=x=2,即可解决问题.
19.【答案】(1)解:如图,连结OB.
∵弦BC垂直于半径OA,
∴BE=CE, = ,
又∵∠ADB=30°,
∴∠AOC=∠AOB=2∠ADB=60°;
(2)解:∵BC=6,
∴CE= BC=3.
∵在Rt△OCE中,∠AOC=60°,
∴∠OCE=30°,
∴OE= OC.
∵OE2+CE2=OC2,
∴ +32=OC2,
∴解得:OC= .
∵ = ,
∴∠BOC=2∠AOC=120°,
∴ 的长= (cm).
【解析】【分析】(1)由在⊙O中,弦BC垂直于半径OA,根据垂径定理可得 = ,则可求得∠AOC的度数;(2)首先连接OB,由弦BC=6cm,可求得半径的长,继而求得图中劣弧 的长.
20.【答案】(1)解:∵AB=AC,
∴ ,
∵AF为⊙O的直径,
∴AF⊥BC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∠AD⊥AF,
∴AD是⊙O的切线
(2)解:连接OC,OB,
∵∠BAC=45°,
∴∠BOC=90°,
∵AF=2,
∴OB=OC=1,
∴BC= ,
∵四边形ABCD是平行四边形,
∴AD=BC= ,
连接OE,
∵AB∥BD,
∴∠ACE=∠BAC=45°,
∴∠AOE=2∠ACE=90°,
∵OA=OE=1,
∴阴影部分的面积=S梯形AOED﹣S扇形AOE= (1+ )×1﹣ =
【解析】【分析】(1)由题意根据垂径定理得到AF⊥BC,根据平行四边形的性质得到AD∥BC,求得AD⊥AF,于是得到AD是⊙O的切线;(2)根据题意连接OC,OB,根据圆周角定理得到∠BOC=90°,根据勾股定理得到BC= ,求得AD=BC= ,连接OE,根据梯形和扇形的面积公式即可得到结论..
21.【答案】(1)解:∵AB=4,
∴OB=2
∵∠COB=60°,
∴S扇形OBC= =
(2)解:∵AC平分∠FAB,
∴∠FAC=∠CAO,
∵AO=CO,
∴∠ACO=∠CAO
∴∠FAC=∠ACO
∴AD∥OC,
∵CD⊥AF,
∴CD⊥OC
∵C在圆上,
∴CD是⊙O的切线
【解析】【分析】(1)根据扇形面积=可求解;
(2)要证 CD是⊙O的切线 ,由切线的判定只需证 CD⊥OC 即可。由已知条件易证 AD∥OC,而CD⊥AF, 所以 CD⊥OC ,则结论可得证。
22.【答案】(1)解:如图所示:
(2)解:AB与⊙O的位置关系是相切.
∵AO是∠BAC的平分线,∠ACB=90°,∠ADO=90°,
∴DO=CO,
∴AB与⊙O相切;
(3)3
【解析】【解答】综合运用:(3)设半径为x,则,,,
在中,,
,
在中,,
解得:.
⊙O的半径为3.
【分析】(1)根据题意作图即可;
(2)证明∠ADO=90°,DO=CO,即可得到AB与⊙O相切;
(3)设半径为x,则,,,利用勾股定理可得,再求出x的值即可。
23.【答案】(1)证明:连接OD,如图,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴△BDC为直角三角形,
∵E为BC边上的中点,
∴ED=EC
(2)证明:∵DE=EC,
∴∠EDC=∠ECD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠EDC+∠ODC=∠ECD+∠OCD,
即∠ODE=∠OCE=90°,
∴OD⊥DE,
∴DE是⊙O的切线
(3)解:在Rt△ABC中,CD⊥AB,
∴AC2=AD×AB,
∵OA= DB,
∴AC=2 DB,
∴20DB2=AD(AD+DB),
整理得,AD2+DB DB-20DB2=0,
∴(AD+5DB)(AD-4DB)=0,
∴AD=4DB,AD=-5DB(舍去),
∵DC2=AC2-AD2
∴DC=2DB,
∴tanB=
【解析】【分析】(1)连接OD,如图,利用圆周角定理可判定△BDC为直角三角形,再利用直角三角形斜边上的中线性质得ED=EB; (2)根据等腰三角形的性质得∠EDC=∠ECD,∠OCD=∠ODC,于是可得到∠ODE=∠OCE=90°,然后根据切线的判定方法可判断DE是⊙O的切线; (3)利用射影定理表示出AD,利用勾股定理表示出DC,即可求得tanB的值.
一、单选题
1.已知⊙O的半径为4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
2.若的半径为5,点到圆心的距离为,当点在圆上时,则有( ).
A. B. C. D.
3.一个圆锥的底面半径为 ,母线长为 ,这个圆锥的侧面积为( )
A. B. C. D.
4.若扇形的半径为4,圆心角为90°,则此扇形的弧长是( )
A.π B.2π C.4π D.8π
5.已知⊙O的半径为5cm,若OP=3cm,则点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O上 C.点P在⊙O内 D.不能确定
6.给出下列命题:①反比例函数的图象经过一、三象限,且y随x的增大而减小;②对角线相等且有一个内角是直角的四边形是矩形;③我国古代三国时期的数学家赵爽,创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明(右图);④相等的弧所对的圆周角相等.其中正确的是( )
A.③④ B.①②③ C.②④ D.①②③④
7.如图,在平面直角坐标系中,点爿是双曲线y= 上的一点,以点爿为圆心,0A为半径画圆。交两坐标轴于点B,C.若OB=8,则OC的长为( )
A.2 B.4 C.2 D.6
8.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=20°,则∠D等于( )
A.20° B.30° C.50° D.40°
9.如图,A、B、C是⊙O上的三点,已知 ,则 ( )
A.15° B. C. D.
10.如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知 和 所对的圆心角分别为90°和50°,则∠P=( )
A.45° B.40° C.25° D.20°
二、填空题
11.如图,扇形纸叠扇完全打开后,扇形ABC的面积为300πcm2,∠BAC=120°,BD=2AD,则BD的长度为 cm.
12.如图,为半圆内一点,为圆心,直径长为,,,将绕圆心逆时针旋转至,点在上,则边扫过区域图中阴影部分的面积为 结果保留
13.一个扇形的面积为,半径长为,则这个扇形的圆心角为 .
14.如图,四边形ABCD是⊙O的内接四边形,点D是 的中点,点E是 上的一点,若∠CED=40°,则∠ADC= 度.
三、解答题
15.如图,⊙O的弦AB和弦CD相交于点E,AB=CD,求证:AD=CB
16.如图,PA,PB分别与⊙O相切于点A,B,连接AB,∠APB=60°,AB=5,求PA的长.
17.已知:如图, 、 为 的半径, 、 分别为 、 的中点.求证: .
18.如图1,⊙O的半径r=,弦AB、CD交于点E,C为弧AB的中点,过D点的直线交AB延长线于点F,且DF=EF.
(1)试判断DF与⊙O的位置关系,并说明理由;
(2)如图2,连接AC,若AC∥DF,BE=AE,求CE的长.
四、综合题
19.如图,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧BC上一点,连结BD,AD,OC,∠ADB=30°.
(1)求∠AOC的度数;
(2)若弦BC=6 cm,求图中劣弧BC的长.
20.如图,AB=AC,⊙O为△ABC的外接圆,AF为⊙O的直径,四边形ABCD是平行四边形.
(1)求证:AD是⊙O的切线;
(2)若∠BAC=45°,AF=2,求阴影部分的面积.
21.已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.
(1)求扇形OBC的面积(结果保留π);
(2)求证:CD是⊙O的切线.
22.如图:
(1)实践操作:如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.
(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点O.
②以O为圆心,OC为半径作圆.
(2)综合运用:在你所作的图中,直线AB与⊙O存在怎样的位置关系,请说明理由.
(3)若AC=6,BC=8,则⊙O的半径为 .
23.如图,AC是⊙O的直径,AD是⊙O的弦,过点C作CB⊥AC交AD的延长线于点B,点E为BC的中点,连接DE、DC.
(1)求证:ED=EC.
(2)求证:DE是⊙O的切线.
(3)若OA= DB,求tanB的值.
答案解析部分
1.【答案】A
【解析】【分析】设圆的半径为R,圆心到直线的距离为d:当d
∵3<4
∴直线l与⊙O的位置关系是相交.
故选A.
【点评】本题属于基础应用题,只需学生熟练掌握直线与圆的位置关系,即可完成。
2.【答案】C
【解析】【解答】解: 若的半径为5,点P到圆心的距离为d,当点P在圆上时,则有d=5.
故答案为:C.
【分析】 如果用r表示圆的半径,d表示同一平面内一点到圆心的距离,则 d>r 点在圆外, d=r 点在圆上 d<r 点在圆内,据此可得答案.
3.【答案】B
【解析】【解答】解:这个圆锥的侧面积=π×3×5=15πcm2,
故答案为:B.
【分析】圆锥侧面积公式S=πrl代入即可,其中r为圆锥的底面半径 ,l为母线长.
4.【答案】B
【解析】【分析】扇形的弧长=,把相应数值代入即可求解.
扇形的弧长=,
故选B.
5.【答案】C
【解析】【解答】解:∵点P到圆心的距离d=3<5=r,
∴该点P在⊙O内.
故答案为:C.
【分析】根据点到圆心的距离和圆的半径之间的数量关系,即可判断点和圆的位置关系,由题知点P到圆心的距离小于半径,可得出点P在⊙O内.
6.【答案】A
【解析】【分析】分别根据反比例函数的性质、矩形的性质及勾股定理、圆心角、弧、弦的关系对每小题进行逐一解答.
【解答】①反比例函数y= 的图象的图象两个分支分别位于一、三象限,而不是经过一、三象限,故此小题错误;
②两条对角线互相平分且有一个角是直角的四边形是矩形,对角线相等且有一个内角是直角的四边形有可能是梯形,故此小题错误;
③符合勾股定理的历史,故此小题正确;
④符合圆心角、弧、弦的关系,故此小题正确.
所以③④正确.
故选A.
7.【答案】B
【解析】【解答】解:过点A作AD⊥OB于点D,连接CB
∵∠COB=90°
∴BC是直径,点C、B、A在同一条直线上,
∵OB=8
∴OD=OB=4
当x=4时,y=8÷4=2
∴点A(4,2)
设yAB=kx+b
由题意得:
解之:
∴yAB=x+4
当x=0时,则y=4
∴点C(0,4)
∴OC=4
故答案为:B
【分析】过点A作AD⊥OB于点D,连接CB,利用圆周角定理可证得BC是直径,点C、B、A在同一条直线上,再利用垂径定理求出OD的长,就可得到点A的横坐标,利用函数解析式求出点A的纵坐标,就可得到点A的坐标,然后利用待定系数法求出直线AB的函数解析式,就可求出直线AB与y轴的交点C的坐标,从而可求出OC的长。
8.【答案】C
【解析】【解答】解:连接OC,
∵DC切⊙O于点C,
∴∠OCD=90°,
∵∠A=20°,
∴∠OCA=20°,
∴∠DOC=40°,
∴∠D=90°-40°=50°.
故答案为:C.
【分析】连接OC,根据切线的性质可得∠OCD=90°,根据等腰三角形的性质可得∠A=∠OCA=20°,结合外角的性质可得∠DOC=40°,然后根据余角的性质进行计算.
9.【答案】D
【解析】【解答】∵∠O=60°,
∴∠C=∠O=×60°=30°,
故答案为:D.
【分析】根据同弧所对的圆周角等于圆心角的一半.即可得出答案.
10.【答案】D
【解析】【解答】解:∵ 和 所对的圆心角分别为90°和50°,
∴∠A=25°,∠ADB=45°,
∵∠P+∠A=∠ADB,
∴∠P=∠ADB﹣∠P=45°﹣25°=20°.
故选D.
【分析】先由圆周角定理求出∠A与∠ADB的度数,然后根据三角形外角的性质即可求出∠P的度数.
11.【答案】20
【解析】【解答】解:设AD=x,则AB=3x.
由题意300π= ,
解得x=10,
∴BD=2x=20cm.
故答案为20.
【分析】根据BD=2AD可设AD=x,则AB=3x,由扇形的面积=可求出x的值,则BD的长度可求。
12.【答案】
【解析】【解答】解:∵,将绕圆心逆时针旋转至,
∴∠B'OC'=60°,△BOC≌△B'OC',
∴∠B'OC=180°-60°-60°=60°,
∴∠C'B'O=90°-60°=30°,∠B'OB=∠BOC+∠B'OC=120°,
∵AB=2cm,
∴OB=1cm,OC'=cm,
∴,
∴,,
∴,
故答案为:.
【分析】根据旋转的性质求出∠B'OC'=60°,△BOC≌△B'OC',再利用全等三角形的性质以及扇形面积公式等计算求解即可。
13.【答案】80°
【解析】【解答】解:扇形所在圆的面积为: ,
扇形的圆心角度数为: ,
故答案为:80°.
【分析】先求出整圆的面积,再求出扇形的面积占整圆面积的百分比,最后乘以360°即可得到答案。
14.【答案】100
【解析】【解答】解:如图,
连接AE,
∵点D是 的中点,
∴∠AED=∠CED,
∵∠CED=40°,
∴∠AEC=2∠CED=80°,
∵四边形ADCE是圆内接四边形,
∴∠ADC+∠AEC=180°,
∴∠ADC=180°﹣∠AEC=100°,
故答案为:100.
【分析】连接AE,先求得∠CED,再求得∠AEC,最后根据圆内接四边形对角互补求得∠ADC即可。
15.【答案】证明:∵AB=CD
∴
∴
∴ =
∴AD=BC.
【解析】【分析】由圆心角、弦、弧之间的关系定理可得和弧的构成可求解.
16.【答案】解:∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,
∴AB=PA=5
【解析】【分析】由切线长定理可得PA=PB,由∠APB=60°可得△PAB是等边三角形,从而得出答案.
17.【答案】证明:∵ , 为 的半径, , 分别为 , 的中点,
∴ ,
.
在 与 中,
∵ ,
∴ .
∴ .
【解析】【分析】先利用边角边定理证明△AOD≌△BOC,则由全等三角形的性质即可得出∠A=∠B.
18.【答案】证明:(1)如图1,连接OC、OD;∵C为弧AB的中点,∴OC⊥AB,∠OCE+∠AEC=90°;∴DF=EF,∴∠FDE=∠FED=∠AEC;∵OA=OC,∴∠OCE=∠ODC,∴∠ODC+∠CDF=90°,即OD⊥DF,∴DF与⊙O相切.(2)如图2,连接OA、OC;由(1)知OC⊥AB,∴AH=BH;∵AC∥DF,∴∠ACD=∠CDF;而EF=DF,∴∠DEF=∠CDF=∠ACD,∴AC=AE;设AE=5λ,则BE=3λ,∴AH=4λ,HE=λ,AC=AE=5λ;∴由勾股定理得:CH=3λ;CE2=CH2+HE2=9λ2+λ2,∴CE=λ;在直角△AOH中,由勾股定理得:AO2=AH2+OH2,即r2=(r﹣3λ)2+(4λ)2,解得:λ=r=x=2,∴CE=2.
【解析】【分析】(1)如图,作辅助线;证明∠ODC+∠CDF=90°,即可解决问题.
(2)如图,作辅助线;证明OH⊥AB,AH=4λ,此为解题的关键性结论;证明CE=λ;列出方程r2=(r﹣3λ)2+(4λ)2,求出λ=r=x=2,即可解决问题.
19.【答案】(1)解:如图,连结OB.
∵弦BC垂直于半径OA,
∴BE=CE, = ,
又∵∠ADB=30°,
∴∠AOC=∠AOB=2∠ADB=60°;
(2)解:∵BC=6,
∴CE= BC=3.
∵在Rt△OCE中,∠AOC=60°,
∴∠OCE=30°,
∴OE= OC.
∵OE2+CE2=OC2,
∴ +32=OC2,
∴解得:OC= .
∵ = ,
∴∠BOC=2∠AOC=120°,
∴ 的长= (cm).
【解析】【分析】(1)由在⊙O中,弦BC垂直于半径OA,根据垂径定理可得 = ,则可求得∠AOC的度数;(2)首先连接OB,由弦BC=6cm,可求得半径的长,继而求得图中劣弧 的长.
20.【答案】(1)解:∵AB=AC,
∴ ,
∵AF为⊙O的直径,
∴AF⊥BC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∠AD⊥AF,
∴AD是⊙O的切线
(2)解:连接OC,OB,
∵∠BAC=45°,
∴∠BOC=90°,
∵AF=2,
∴OB=OC=1,
∴BC= ,
∵四边形ABCD是平行四边形,
∴AD=BC= ,
连接OE,
∵AB∥BD,
∴∠ACE=∠BAC=45°,
∴∠AOE=2∠ACE=90°,
∵OA=OE=1,
∴阴影部分的面积=S梯形AOED﹣S扇形AOE= (1+ )×1﹣ =
【解析】【分析】(1)由题意根据垂径定理得到AF⊥BC,根据平行四边形的性质得到AD∥BC,求得AD⊥AF,于是得到AD是⊙O的切线;(2)根据题意连接OC,OB,根据圆周角定理得到∠BOC=90°,根据勾股定理得到BC= ,求得AD=BC= ,连接OE,根据梯形和扇形的面积公式即可得到结论..
21.【答案】(1)解:∵AB=4,
∴OB=2
∵∠COB=60°,
∴S扇形OBC= =
(2)解:∵AC平分∠FAB,
∴∠FAC=∠CAO,
∵AO=CO,
∴∠ACO=∠CAO
∴∠FAC=∠ACO
∴AD∥OC,
∵CD⊥AF,
∴CD⊥OC
∵C在圆上,
∴CD是⊙O的切线
【解析】【分析】(1)根据扇形面积=可求解;
(2)要证 CD是⊙O的切线 ,由切线的判定只需证 CD⊥OC 即可。由已知条件易证 AD∥OC,而CD⊥AF, 所以 CD⊥OC ,则结论可得证。
22.【答案】(1)解:如图所示:
(2)解:AB与⊙O的位置关系是相切.
∵AO是∠BAC的平分线,∠ACB=90°,∠ADO=90°,
∴DO=CO,
∴AB与⊙O相切;
(3)3
【解析】【解答】综合运用:(3)设半径为x,则,,,
在中,,
,
在中,,
解得:.
⊙O的半径为3.
【分析】(1)根据题意作图即可;
(2)证明∠ADO=90°,DO=CO,即可得到AB与⊙O相切;
(3)设半径为x,则,,,利用勾股定理可得,再求出x的值即可。
23.【答案】(1)证明:连接OD,如图,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴△BDC为直角三角形,
∵E为BC边上的中点,
∴ED=EC
(2)证明:∵DE=EC,
∴∠EDC=∠ECD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠EDC+∠ODC=∠ECD+∠OCD,
即∠ODE=∠OCE=90°,
∴OD⊥DE,
∴DE是⊙O的切线
(3)解:在Rt△ABC中,CD⊥AB,
∴AC2=AD×AB,
∵OA= DB,
∴AC=2 DB,
∴20DB2=AD(AD+DB),
整理得,AD2+DB DB-20DB2=0,
∴(AD+5DB)(AD-4DB)=0,
∴AD=4DB,AD=-5DB(舍去),
∵DC2=AC2-AD2
∴DC=2DB,
∴tanB=
【解析】【分析】(1)连接OD,如图,利用圆周角定理可判定△BDC为直角三角形,再利用直角三角形斜边上的中线性质得ED=EB; (2)根据等腰三角形的性质得∠EDC=∠ECD,∠OCD=∠ODC,于是可得到∠ODE=∠OCE=90°,然后根据切线的判定方法可判断DE是⊙O的切线; (3)利用射影定理表示出AD,利用勾股定理表示出DC,即可求得tanB的值.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
