第四章 图形的相似 期末复习解答题专练 2023-2024学年北师大版九年级数学上册(无答案)
文档属性
| 名称 | 第四章 图形的相似 期末复习解答题专练 2023-2024学年北师大版九年级数学上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 933.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 11:25:12 | ||
图片预览



文档简介
第四章 图形的相似 期末复习解答题专练 2023-2024学年北师大版九年级数学上册
1、如图,已知的顶点E在的边BC上,DE与AB相交于点F,,.
(1)若,求AE;
(2)求证:.
2、在和中,,,.
(1)判断这两个三角形是否相似?并说明为什么?
(2)能否分别过在这两个三角形中各作一条辅助线,使分割成的两个三角形与分割成的两个三角形分别对应相似?证明你的结论.
3、如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点E在AC边上,∠ADE=45°.过E作ED的垂线交BC延长线于点F,交AD于点G,交AB于点H.
(1)求证∠FDE=∠AEH;
(2)求证EF=GH;
(3)若EG=kGH,求的值(用含k的式子表示).
4、如图,BD,AC相交于点P,连接AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP;
(2)直接回答△ADP与△BCP是不是位似图形;
(3)若AB=8,CD=4,DP=3,求AP的长.
5、一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件,如图①,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)如果把它加工成矩形零件,如图②,当EG为多少时,矩形EGHF有最大面积?最大面积是多少?
6、如图,在 ABCD中,AC,BD交于点O,点M是AD的中点,连接MC交BD于点N,ON=1.
(1)求证:△DMN∽△BCN;
(2)求BD的长;
(3)若△DCN的面积为2,直接写出四边形ABNM的面积.
7、如图,在中,,,CD是AB边上的高,点E为线段CD上一点(不与点C,点D重合),连接BE,作与AC的延长线交于点F,与BC交于点G,连接BF.
(1)求证:;
(2)求证:;
(3)求的值.
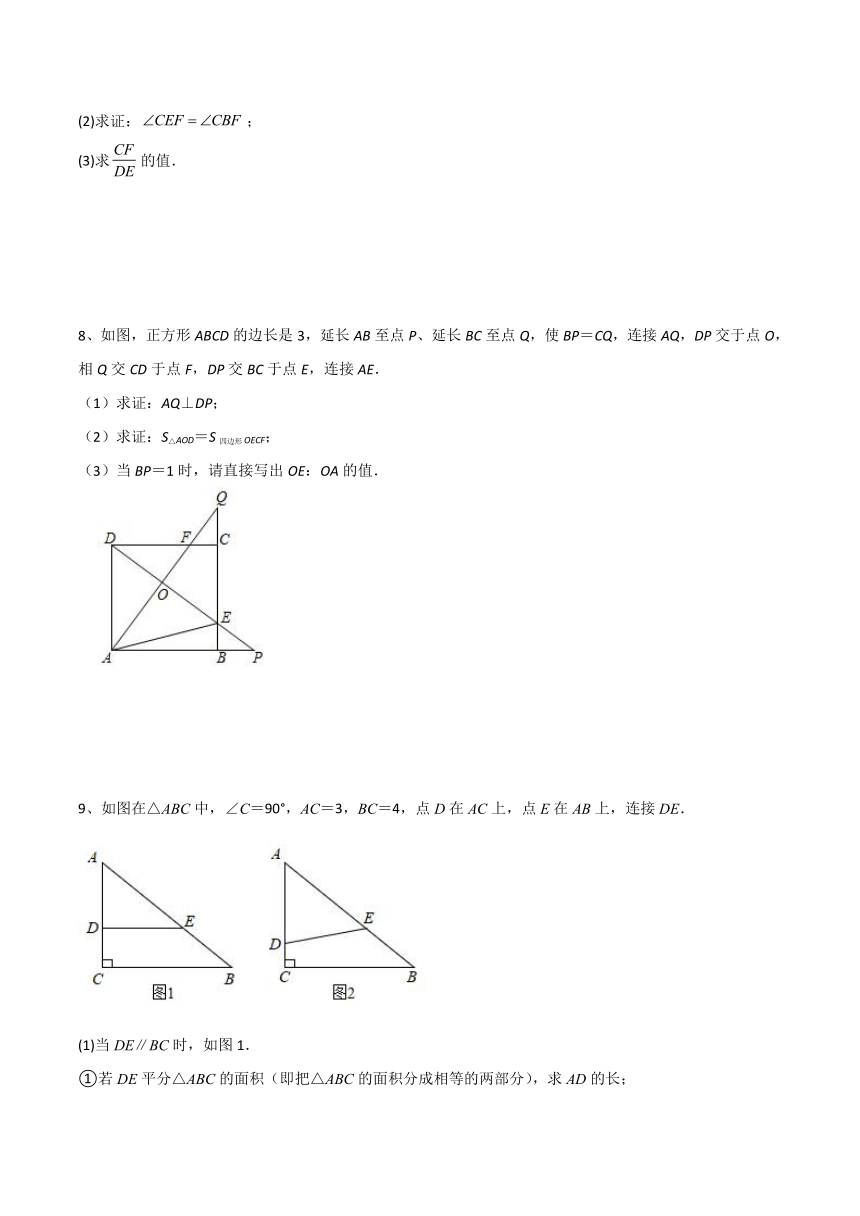
8、如图,正方形ABCD的边长是3,延长AB至点P、延长BC至点Q,使BP=CQ,连接AQ,DP交于点O,相Q交CD于点F,DP交BC于点E,连接AE.
(1)求证:AQ⊥DP;
(2)求证:S△AOD=S四边形OECF;
(3)当BP=1时,请直接写出OE:OA的值.
9、如图在△ABC中,∠C=90°,AC=3,BC=4,点D在AC上,点E在AB上,连接DE.
(1)当DE∥BC时,如图1.
①若DE平分△ABC的面积(即把△ABC的面积分成相等的两部分),求AD的长;
②若DE平分△ABC的周长,求AD的长;
(2)如图2,试问:是否存在DE将△ABC的周长和面积同时平分?若存在,求出AD的长;若不存在,请说明理由.
10、如图,在中,,,,动点P从点A开始沿着边AB向点B以的速度移动(不与点B重合),动点Q从点B开始沿着边BC向点C以的速度移动(不与点C重合).若P、Q两点同时移动.
(1)当移动几秒时,△BPQ的面积为.
(2)设四边形APQC的面积为,当移动几秒时,四边形APQC的面积为?
(3)当移动几秒时,△BPQ与相似?
11、如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,点C是线段上一点,把沿直线翻折,点O恰好落在上的点D处,为折痕.
(1)求线段的长;
(2)求直线的解析式;
(3)若M是射线上的一个动点,在坐标平面内是否存在点P,使以A,B,M,P为顶点的四边形是以为一边的矩形?若存在,请求出点P的坐标;若不存在,请说明理由.
12、如图1,在矩形ABCD中,,,点E在AB边上,且.点F是BC边上的动点.将沿EF折叠得到.直线GF与直线AB的交点为H.
(1)如图2,点F与点C重合时,求与的面积比;
(2)如图3,当H在点A的上方,且满足三角形HEF是等腰三角形时,求线段EH的长.
(3)在点F的运动过程中,以E、G、H为顶点的三角形能否与以B、C、D为顶点的三角形相似?若能,求BF的长;若不存在,请说明理由
13、如图,在平面直角坐标系中,一次函数的图象与x轴交于点A,与y轴交于点,与直线OC交于点.
(1)求直线AB的函数表达式;
(2)过点C作轴于点D,将沿射线CB平移得到的三角形记为,点A,C,D的对应点分别为,,,若与重叠部分的面积为S,平移的距离,当点与点B重合时停止运动.
①若直线交直线OC于点E,则线段的长为________(用含有m的代数式表示);
②当时,S与m的关系式为________;
③当时,m的值为________.
14、【问题探究】数学实践小组的同学利用一张宽的矩形纸片进行了如下的操作写探究:
第一步:如图1,将该矩形纸片沿过点D的直线折叠,使点A落在上的点处,得到折痕,然后把纸片展平.
第二步:如图2,将图1中的矩形纸片沿过点E的直线折叠,使点C恰好落在上的点处,点B落在点处,得到折痕,交于点M,交于点N,再把纸片展平.
(1)【问题解决】
如图1,填空:四边形的形状是__________.
(2)如图2,小明连接了,E两点,发现线段写是相等的.
①请帮助小明写出证明过程;
②如图2,若,求的值.
(3)【问题延伸】如图3,若该矩形纸片的长,点Q在边上,且,P是边上的动点(不与点A,B重合).现将纸片沿折叠,使点B,C分别落在点,处.在点P从点A向点B运动的过程中,若边与边交于点E,则点E相应运动的路径长为__________.
15、某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形和等腰直角三角形,按如图1的方式摆放,,随后保持不动,将绕点C按逆时针方向旋转(),连接,,延长交于点F,连接.该数学兴趣小组进行如下探究,请你帮忙解答:
(1)【初步探究】如图2,当时,则_____;
(2)【初步探究】如图3,当点E,F重合时,请直接写出,,之间的数量关系:_________;
(3)【深入探究】如图4,当点E,F不重合时,(2)中的结论是否仍然成立?若成立,请给出推理过程;若不成立,请说明理由.
(4)【拓展延伸】如图5,在与中,,若,(m为常数).保持不动,将绕点C按逆时针方向旋转(),连接,,延长交于点F,连接,如图6.试探究,,之间的数量关系,并说明理由.
1、如图,已知的顶点E在的边BC上,DE与AB相交于点F,,.
(1)若,求AE;
(2)求证:.
2、在和中,,,.
(1)判断这两个三角形是否相似?并说明为什么?
(2)能否分别过在这两个三角形中各作一条辅助线,使分割成的两个三角形与分割成的两个三角形分别对应相似?证明你的结论.
3、如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点E在AC边上,∠ADE=45°.过E作ED的垂线交BC延长线于点F,交AD于点G,交AB于点H.
(1)求证∠FDE=∠AEH;
(2)求证EF=GH;
(3)若EG=kGH,求的值(用含k的式子表示).
4、如图,BD,AC相交于点P,连接AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP;
(2)直接回答△ADP与△BCP是不是位似图形;
(3)若AB=8,CD=4,DP=3,求AP的长.
5、一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件,如图①,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)如果把它加工成矩形零件,如图②,当EG为多少时,矩形EGHF有最大面积?最大面积是多少?
6、如图,在 ABCD中,AC,BD交于点O,点M是AD的中点,连接MC交BD于点N,ON=1.
(1)求证:△DMN∽△BCN;
(2)求BD的长;
(3)若△DCN的面积为2,直接写出四边形ABNM的面积.
7、如图,在中,,,CD是AB边上的高,点E为线段CD上一点(不与点C,点D重合),连接BE,作与AC的延长线交于点F,与BC交于点G,连接BF.
(1)求证:;
(2)求证:;
(3)求的值.
8、如图,正方形ABCD的边长是3,延长AB至点P、延长BC至点Q,使BP=CQ,连接AQ,DP交于点O,相Q交CD于点F,DP交BC于点E,连接AE.
(1)求证:AQ⊥DP;
(2)求证:S△AOD=S四边形OECF;
(3)当BP=1时,请直接写出OE:OA的值.
9、如图在△ABC中,∠C=90°,AC=3,BC=4,点D在AC上,点E在AB上,连接DE.
(1)当DE∥BC时,如图1.
①若DE平分△ABC的面积(即把△ABC的面积分成相等的两部分),求AD的长;
②若DE平分△ABC的周长,求AD的长;
(2)如图2,试问:是否存在DE将△ABC的周长和面积同时平分?若存在,求出AD的长;若不存在,请说明理由.
10、如图,在中,,,,动点P从点A开始沿着边AB向点B以的速度移动(不与点B重合),动点Q从点B开始沿着边BC向点C以的速度移动(不与点C重合).若P、Q两点同时移动.
(1)当移动几秒时,△BPQ的面积为.
(2)设四边形APQC的面积为,当移动几秒时,四边形APQC的面积为?
(3)当移动几秒时,△BPQ与相似?
11、如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,点C是线段上一点,把沿直线翻折,点O恰好落在上的点D处,为折痕.
(1)求线段的长;
(2)求直线的解析式;
(3)若M是射线上的一个动点,在坐标平面内是否存在点P,使以A,B,M,P为顶点的四边形是以为一边的矩形?若存在,请求出点P的坐标;若不存在,请说明理由.
12、如图1,在矩形ABCD中,,,点E在AB边上,且.点F是BC边上的动点.将沿EF折叠得到.直线GF与直线AB的交点为H.
(1)如图2,点F与点C重合时,求与的面积比;
(2)如图3,当H在点A的上方,且满足三角形HEF是等腰三角形时,求线段EH的长.
(3)在点F的运动过程中,以E、G、H为顶点的三角形能否与以B、C、D为顶点的三角形相似?若能,求BF的长;若不存在,请说明理由
13、如图,在平面直角坐标系中,一次函数的图象与x轴交于点A,与y轴交于点,与直线OC交于点.
(1)求直线AB的函数表达式;
(2)过点C作轴于点D,将沿射线CB平移得到的三角形记为,点A,C,D的对应点分别为,,,若与重叠部分的面积为S,平移的距离,当点与点B重合时停止运动.
①若直线交直线OC于点E,则线段的长为________(用含有m的代数式表示);
②当时,S与m的关系式为________;
③当时,m的值为________.
14、【问题探究】数学实践小组的同学利用一张宽的矩形纸片进行了如下的操作写探究:
第一步:如图1,将该矩形纸片沿过点D的直线折叠,使点A落在上的点处,得到折痕,然后把纸片展平.
第二步:如图2,将图1中的矩形纸片沿过点E的直线折叠,使点C恰好落在上的点处,点B落在点处,得到折痕,交于点M,交于点N,再把纸片展平.
(1)【问题解决】
如图1,填空:四边形的形状是__________.
(2)如图2,小明连接了,E两点,发现线段写是相等的.
①请帮助小明写出证明过程;
②如图2,若,求的值.
(3)【问题延伸】如图3,若该矩形纸片的长,点Q在边上,且,P是边上的动点(不与点A,B重合).现将纸片沿折叠,使点B,C分别落在点,处.在点P从点A向点B运动的过程中,若边与边交于点E,则点E相应运动的路径长为__________.
15、某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形和等腰直角三角形,按如图1的方式摆放,,随后保持不动,将绕点C按逆时针方向旋转(),连接,,延长交于点F,连接.该数学兴趣小组进行如下探究,请你帮忙解答:
(1)【初步探究】如图2,当时,则_____;
(2)【初步探究】如图3,当点E,F重合时,请直接写出,,之间的数量关系:_________;
(3)【深入探究】如图4,当点E,F不重合时,(2)中的结论是否仍然成立?若成立,请给出推理过程;若不成立,请说明理由.
(4)【拓展延伸】如图5,在与中,,若,(m为常数).保持不动,将绕点C按逆时针方向旋转(),连接,,延长交于点F,连接,如图6.试探究,,之间的数量关系,并说明理由.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
