第十二章全等三角形期末复习单元训练试卷2023—2024学年人教版数学八年级上册(含答案)
文档属性
| 名称 | 第十二章全等三角形期末复习单元训练试卷2023—2024学年人教版数学八年级上册(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 853.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 13:05:25 | ||
图片预览

文档简介
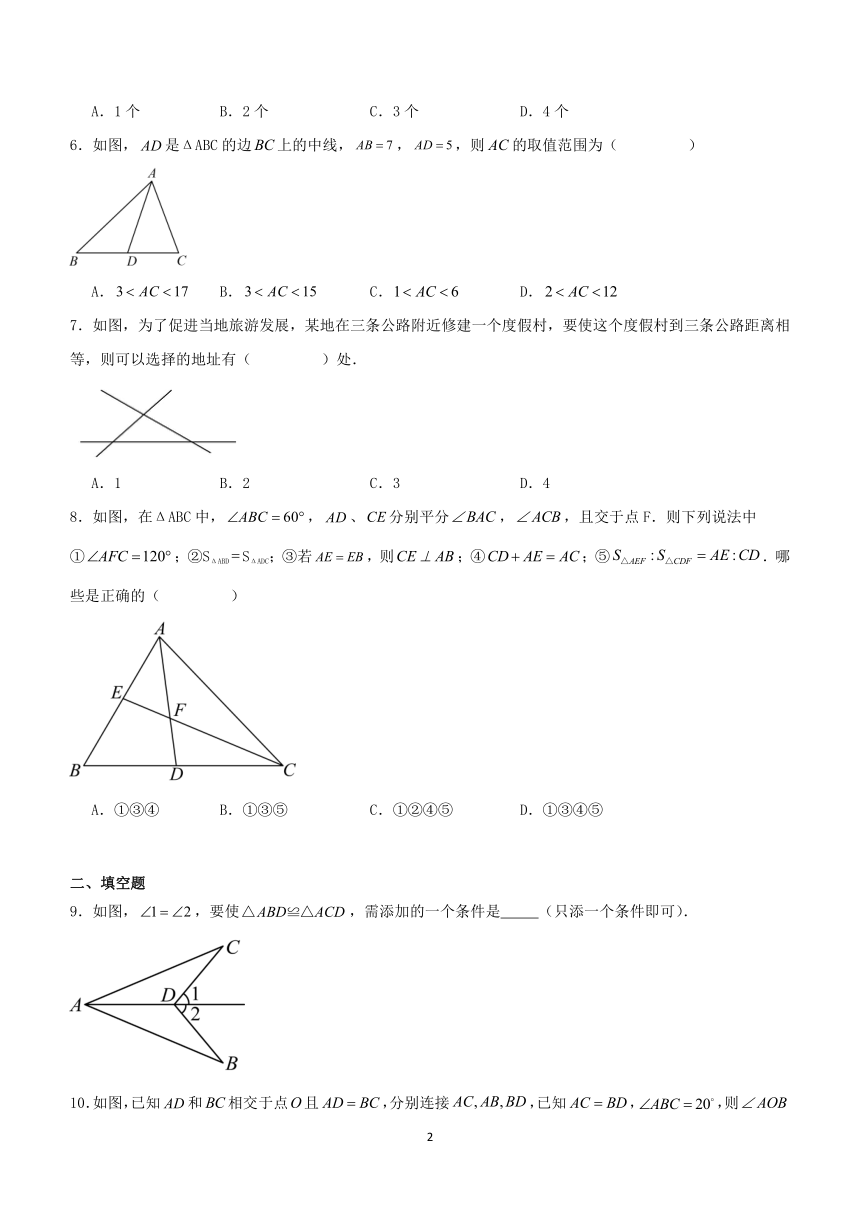
第十二章 全等三角形 期末复习单元训练试卷
一、单选题
1.如图各组两个图形属于全等形的是( )
A. B.
C. D.
2.若△ABC≌△DEF,则下列说法不正确的是( )
A.和是对应角 B.AB和DE是对应边
C.点C和点F是对应顶点 D.和是对应角
3.如图,ΔAODΔBOC,若,则的长度是( )
A.3 B.4 C.5 D.6
4.在ΔABC中,,将ΔABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( ).
A. B.
C. D.
5.如图,是ΔABC的角平分线,过点D作于E,于F,则下列结论:①;②;③;④,其中错误结论的个数有( )
A.1个 B.2个 C.3个 D.4个
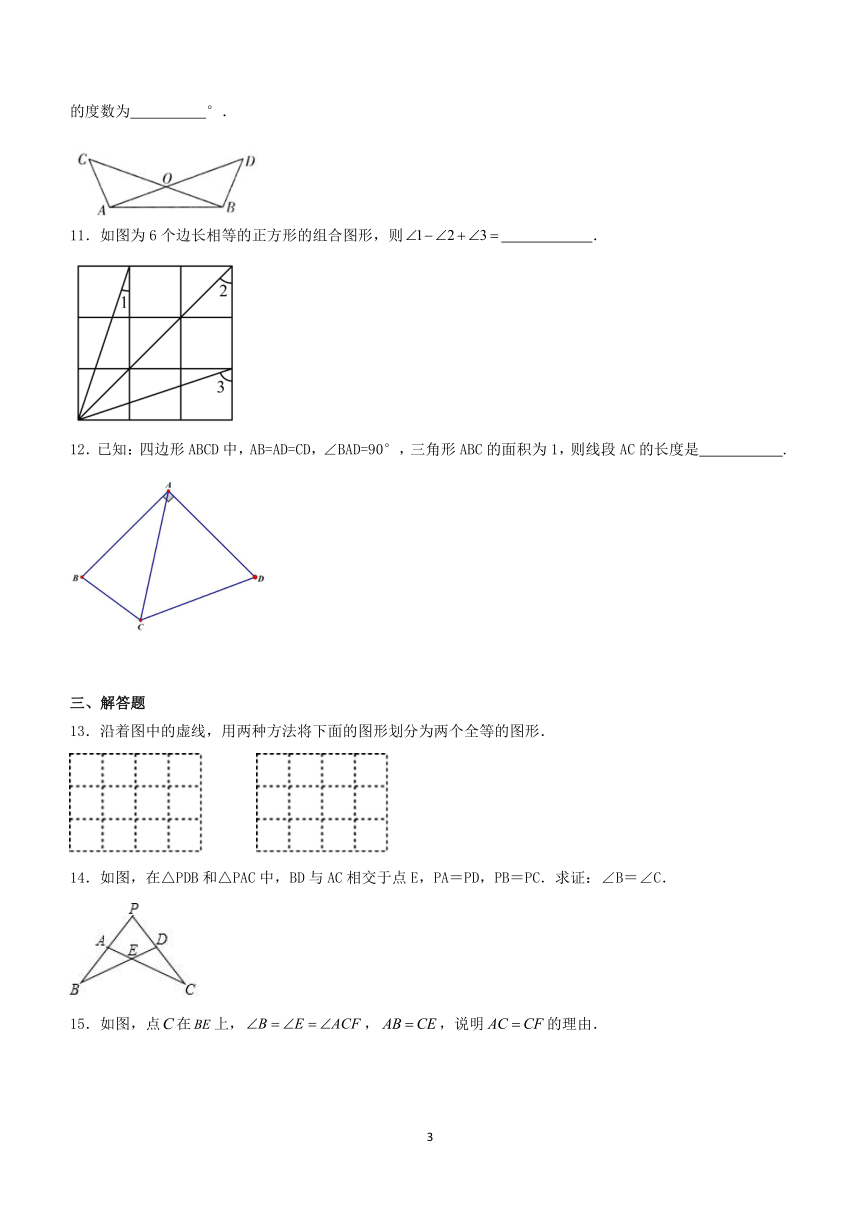
6.如图,是ΔABC的边上的中线,,,则的取值范围为( )
A. B. C. D.
7.如图,为了促进当地旅游发展,某地在三条公路附近修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.
A.1 B.2 C.3 D.4
8.如图,在ΔABC中,,、分别平分,,且交于点F.则下列说法中①;②SΔABDSΔADC;③若,则;④;⑤.哪些是正确的( )
A.①③④ B.①③⑤ C.①②④⑤ D.①③④⑤
二、填空题
9.如图,,要使,需添加的一个条件是 (只添一个条件即可).
10.如图,已知和相交于点且,分别连接,已知,,则的度数为 °.
11.如图为6个边长相等的正方形的组合图形,则 .
12.已知:四边形ABCD中,AB=AD=CD,∠BAD=90°,三角形ABC的面积为1,则线段AC的长度是 .
三、解答题
13.沿着图中的虚线,用两种方法将下面的图形划分为两个全等的图形.
14.如图,在△PDB和△PAC中,BD与AC相交于点E,PA=PD,PB=PC.求证:∠B=∠C.
15.如图,点在上,,,说明的理由.
16.如图,用尺规作图,并保留作图痕迹,ΔABC中,延长AC到E,使CE=CA,在线段AE与点B相异的一侧作∠CEM=∠A,延长BC交EM于点D,求证:ΔABC≌ΔEDC.
17.如图,在中,,的角平分线交于D,交的角平分线于E,过点E作,交于点F,求证:.
18.如图,在Rt△ABC中,∠BAC=90°,AB=AC,在BC的同侧作任意Rt△DBC,∠BDC=90°.
(1)若CD=2BD,M是CD中点(如图1),求证:△ADB≌△AMC;
下面是小明的证明过程,请你将它补充完整:
证明:设AB与CD相交于点O,
∵∠BDC=90°,∠BAC=90°,
∴∠DOB+∠DBO=∠AOC+∠ACO=90°.
∵∠DOB=∠AOC,
∴∠DBO=∠
∵M是DC的中点,
∴CM=CD=
又∵AB=AC,
∴△ADB≌△AMC.
(2)若CD<BD(如图2),在BD上是否存在一点N,使得△ADN是以DN为斜边的等腰直角三角形?若存在,请在图2中确定点N的位置,并加以证明;若不存在,请说明理由;
(3)当CD≠BD时,线段AD,BD与CD满足怎样的数量关系?请直接写出.
参考答案
1.B
2.A
3.D
4.D
5.A
6.A
7.D
8.D
9.
10.140
11./45度
12.2
13.解:如图所示(任意两种方法,正确即可):
14.证明:在△PDB和△PAC中,
,
∴△PDB≌△PAC(SAS),
∴∠B=∠C.
15.由,,得,从而可证明,最后根据全等三角形的性质即可求解.
16.如图所示即为所求.
证明:在ΔABC和ΔEDC中,∵∠A=∠E,CE=CA,∠ECD=∠CAB,∴ΔABC≌ΔEDC(ASA).
17.延长,相交于点M,分别证明和即可得解.
18.(1)MCA,BD;(2)存在;(3))当CD<BD时AD=BD﹣CD;
当CD>BD时,AD=CD﹣BD
一、单选题
1.如图各组两个图形属于全等形的是( )
A. B.
C. D.
2.若△ABC≌△DEF,则下列说法不正确的是( )
A.和是对应角 B.AB和DE是对应边
C.点C和点F是对应顶点 D.和是对应角
3.如图,ΔAODΔBOC,若,则的长度是( )
A.3 B.4 C.5 D.6
4.在ΔABC中,,将ΔABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( ).
A. B.
C. D.
5.如图,是ΔABC的角平分线,过点D作于E,于F,则下列结论:①;②;③;④,其中错误结论的个数有( )
A.1个 B.2个 C.3个 D.4个
6.如图,是ΔABC的边上的中线,,,则的取值范围为( )
A. B. C. D.
7.如图,为了促进当地旅游发展,某地在三条公路附近修建一个度假村,要使这个度假村到三条公路距离相等,则可以选择的地址有( )处.
A.1 B.2 C.3 D.4
8.如图,在ΔABC中,,、分别平分,,且交于点F.则下列说法中①;②SΔABDSΔADC;③若,则;④;⑤.哪些是正确的( )
A.①③④ B.①③⑤ C.①②④⑤ D.①③④⑤
二、填空题
9.如图,,要使,需添加的一个条件是 (只添一个条件即可).
10.如图,已知和相交于点且,分别连接,已知,,则的度数为 °.
11.如图为6个边长相等的正方形的组合图形,则 .
12.已知:四边形ABCD中,AB=AD=CD,∠BAD=90°,三角形ABC的面积为1,则线段AC的长度是 .
三、解答题
13.沿着图中的虚线,用两种方法将下面的图形划分为两个全等的图形.
14.如图,在△PDB和△PAC中,BD与AC相交于点E,PA=PD,PB=PC.求证:∠B=∠C.
15.如图,点在上,,,说明的理由.
16.如图,用尺规作图,并保留作图痕迹,ΔABC中,延长AC到E,使CE=CA,在线段AE与点B相异的一侧作∠CEM=∠A,延长BC交EM于点D,求证:ΔABC≌ΔEDC.
17.如图,在中,,的角平分线交于D,交的角平分线于E,过点E作,交于点F,求证:.
18.如图,在Rt△ABC中,∠BAC=90°,AB=AC,在BC的同侧作任意Rt△DBC,∠BDC=90°.
(1)若CD=2BD,M是CD中点(如图1),求证:△ADB≌△AMC;
下面是小明的证明过程,请你将它补充完整:
证明:设AB与CD相交于点O,
∵∠BDC=90°,∠BAC=90°,
∴∠DOB+∠DBO=∠AOC+∠ACO=90°.
∵∠DOB=∠AOC,
∴∠DBO=∠
∵M是DC的中点,
∴CM=CD=
又∵AB=AC,
∴△ADB≌△AMC.
(2)若CD<BD(如图2),在BD上是否存在一点N,使得△ADN是以DN为斜边的等腰直角三角形?若存在,请在图2中确定点N的位置,并加以证明;若不存在,请说明理由;
(3)当CD≠BD时,线段AD,BD与CD满足怎样的数量关系?请直接写出.
参考答案
1.B
2.A
3.D
4.D
5.A
6.A
7.D
8.D
9.
10.140
11./45度
12.2
13.解:如图所示(任意两种方法,正确即可):
14.证明:在△PDB和△PAC中,
,
∴△PDB≌△PAC(SAS),
∴∠B=∠C.
15.由,,得,从而可证明,最后根据全等三角形的性质即可求解.
16.如图所示即为所求.
证明:在ΔABC和ΔEDC中,∵∠A=∠E,CE=CA,∠ECD=∠CAB,∴ΔABC≌ΔEDC(ASA).
17.延长,相交于点M,分别证明和即可得解.
18.(1)MCA,BD;(2)存在;(3))当CD<BD时AD=BD﹣CD;
当CD>BD时,AD=CD﹣BD
