5.7 三角函数的应用(2)(22页ppt)
文档属性
| 名称 | 5.7 三角函数的应用(2)(22页ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第5章 三角函数
5.7 三角函数的应用(2)
人教A版(2019)
教学目标
温故知新
物理量 定义 意义
振幅
周期
频率
相位和初相
它是作简谐运动的物体离开平衡位置的最大距离.
A就是这个简谐运动的振幅
它是作简谐运动的物体往复运动一次所需要的时间.
它是作简谐运动的物体在单位时间内往复运动的次数.
ωx+φ称为相位;x=0时的相位φ称为初相.
新知探究
匀速圆周运动、简谐运动和交变电流都是理想化的运动变化现象,可以用三角函数模型准确地描述它们的运动变化规律.在现实生活中也有大量运动变化现象,仅在一定范围内呈现出近似于周期变化的特点,这些现象也可以借助三角函数近似地描述.
分析:如何根据温度变化曲线得到这一天6~14时的最大温差?
图形中的最高点的纵坐标减去最低点的纵坐标就是这一天6~14时的最大温差.
新知探究
解:
⑴由图可知,这段时间的最大温差是30℃-10℃=20℃.
⑵由图可知,最高点、最低点的坐标分别为(14,30),(6,10).
注意:由于是一段曲线近似函数,一定要给出自变量的范围.
初试身手
解:
⑴由图可知,这一天的最大用电量为50万度,最小用电量为30万度.
新知探究
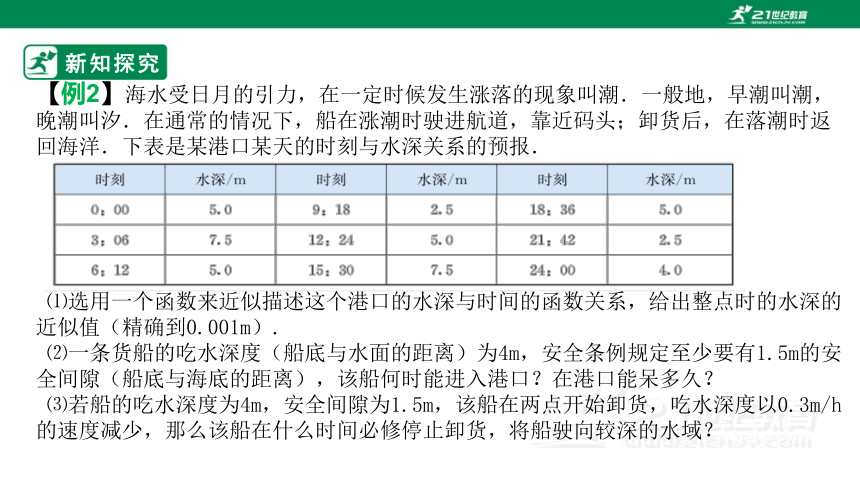
【例2】海水受日月的引力,在一定时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常的情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下表是某港口某天的时刻与水深关系的预报.
⑴选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似值(精确到0.001m).
⑵一条货船的吃水深度(船底与水面的距离)为4m,安全条例规定至少要有1.5m的安全间隙(船底与海底的距离),该船何时能进入港口?在港口能呆多久?
⑶若船的吃水深度为4m,安全间隙为1.5m,该船在两点开始卸货,吃水深度以0.3m/h的速度减少,那么该船在什么时间必修停止卸货,将船驶向较深的水域?
新知探究
解:
新知探究
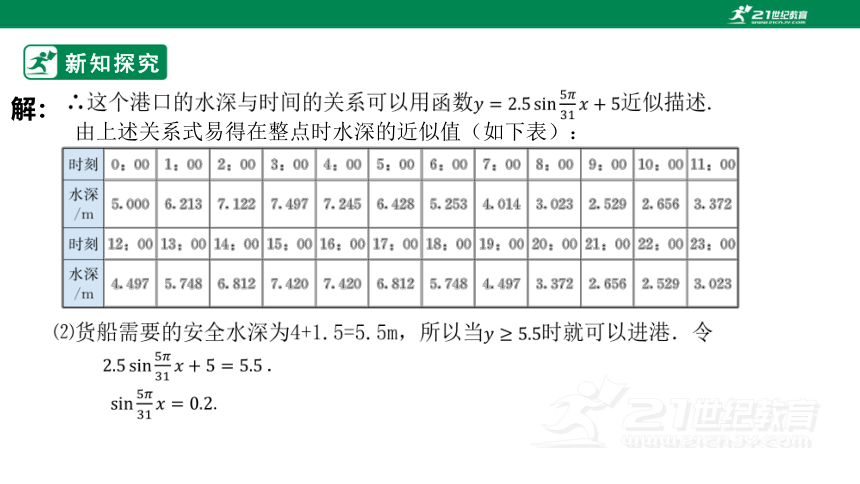
解:
由上述关系式易得在整点时水深的近似值(如下表):
新知探究
解:
因此,货船可以在零时30分左右进港,5时45分左右出港;或在13时左右进港,18时左右出港.每次可以在港口停留5小时左右.
如图,画出两个函数的图象.
新知探究
解:
因此为了安全,货船最好在6.6时之前停止卸货,将船驶向较深的水域.
如图,在同一直角坐标系画出两个函数的图象,可以看到在6~8时之间两个函数图象有一个交点.
借助计算工具,用二分法可以求得点 P的坐标约为(7.016,3.995).
三角函数作为描述现实世界中周期现象得一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测其未来等方面都发挥着十分重要作用.
新知探究
利用三角函数模型解决实际问题的一般步骤
⑴收集整理数据;
⑵画出散点图,建立三角函数模型;
根据收集到的数据找出变化规律,运用已掌握的三角函数知识、物理知识及相关知识建立关系式,将实际问题转化为一个与三角函数有关的数学问题,即建立三角函数模型,从而实现实际问题的数学化.
⑶根据数据和散点图,利用所学的三角函
数知识对得到的三角函数模型予以解答;
⑷用所得三角函数解决实际问题.
初试身手
解:
⑴根据表中数据画出散点图,并用光滑曲线连接起来(如图).
t/时 0 3 6 9 12 15 18 21 24
y/m 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
初试身手
解:
t/时 0 3 6 9 12 15 18 21 24
y/m 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
∴一天内8:00至20:00之间,有6个小时时间对冲浪爱好者开放.
新知探究
解:
【例3】如图,一个大风车的半径为8米,风车按逆时针方向匀速旋转,并且12分钟旋转一周,它的最低点离地面2米,设风车开始旋转时其翼片的一个端点P在风车的最低点,求:
⑴点P离地面距离h(米)与时间t(分钟)之间的函数关系式;
⑵在第一圈的什么时间段点P离地面的高度超过14米?
初试身手
P248 练习
乙点的位置将移至丁点.
初试身手
2解:
观察相应变量区间的三个节律曲线的函数图象进行分析.
为了研究的方便,我们可以统一设A=10,
以出生日为自变量1,计算从出生日到本学期期末考试三天的天数得到三个自变量,
课堂小结
1.数学建模的步骤:
搜集数据,画散点图——观察散点图并进行函数拟合,选择函数模型——利用数据信息,求解函数模型.
2.利用三角函数模型解决实际问题的一般步骤:
3.利用函数模型解决实际问题需要注意,从数学模型中得到的答案还要根据实际情况检验它是否可行.
作业布置
t/s 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
y/cm -4.0 -2.8 0.0 2.8 4.0 2.8 0.0 -2.8 -4.0
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第5章 三角函数
5.7 三角函数的应用(2)
人教A版(2019)
教学目标
温故知新
物理量 定义 意义
振幅
周期
频率
相位和初相
它是作简谐运动的物体离开平衡位置的最大距离.
A就是这个简谐运动的振幅
它是作简谐运动的物体往复运动一次所需要的时间.
它是作简谐运动的物体在单位时间内往复运动的次数.
ωx+φ称为相位;x=0时的相位φ称为初相.
新知探究
匀速圆周运动、简谐运动和交变电流都是理想化的运动变化现象,可以用三角函数模型准确地描述它们的运动变化规律.在现实生活中也有大量运动变化现象,仅在一定范围内呈现出近似于周期变化的特点,这些现象也可以借助三角函数近似地描述.
分析:如何根据温度变化曲线得到这一天6~14时的最大温差?
图形中的最高点的纵坐标减去最低点的纵坐标就是这一天6~14时的最大温差.
新知探究
解:
⑴由图可知,这段时间的最大温差是30℃-10℃=20℃.
⑵由图可知,最高点、最低点的坐标分别为(14,30),(6,10).
注意:由于是一段曲线近似函数,一定要给出自变量的范围.
初试身手
解:
⑴由图可知,这一天的最大用电量为50万度,最小用电量为30万度.
新知探究
【例2】海水受日月的引力,在一定时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常的情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下表是某港口某天的时刻与水深关系的预报.
⑴选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似值(精确到0.001m).
⑵一条货船的吃水深度(船底与水面的距离)为4m,安全条例规定至少要有1.5m的安全间隙(船底与海底的距离),该船何时能进入港口?在港口能呆多久?
⑶若船的吃水深度为4m,安全间隙为1.5m,该船在两点开始卸货,吃水深度以0.3m/h的速度减少,那么该船在什么时间必修停止卸货,将船驶向较深的水域?
新知探究
解:
新知探究
解:
由上述关系式易得在整点时水深的近似值(如下表):
新知探究
解:
因此,货船可以在零时30分左右进港,5时45分左右出港;或在13时左右进港,18时左右出港.每次可以在港口停留5小时左右.
如图,画出两个函数的图象.
新知探究
解:
因此为了安全,货船最好在6.6时之前停止卸货,将船驶向较深的水域.
如图,在同一直角坐标系画出两个函数的图象,可以看到在6~8时之间两个函数图象有一个交点.
借助计算工具,用二分法可以求得点 P的坐标约为(7.016,3.995).
三角函数作为描述现实世界中周期现象得一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测其未来等方面都发挥着十分重要作用.
新知探究
利用三角函数模型解决实际问题的一般步骤
⑴收集整理数据;
⑵画出散点图,建立三角函数模型;
根据收集到的数据找出变化规律,运用已掌握的三角函数知识、物理知识及相关知识建立关系式,将实际问题转化为一个与三角函数有关的数学问题,即建立三角函数模型,从而实现实际问题的数学化.
⑶根据数据和散点图,利用所学的三角函
数知识对得到的三角函数模型予以解答;
⑷用所得三角函数解决实际问题.
初试身手
解:
⑴根据表中数据画出散点图,并用光滑曲线连接起来(如图).
t/时 0 3 6 9 12 15 18 21 24
y/m 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
初试身手
解:
t/时 0 3 6 9 12 15 18 21 24
y/m 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
∴一天内8:00至20:00之间,有6个小时时间对冲浪爱好者开放.
新知探究
解:
【例3】如图,一个大风车的半径为8米,风车按逆时针方向匀速旋转,并且12分钟旋转一周,它的最低点离地面2米,设风车开始旋转时其翼片的一个端点P在风车的最低点,求:
⑴点P离地面距离h(米)与时间t(分钟)之间的函数关系式;
⑵在第一圈的什么时间段点P离地面的高度超过14米?
初试身手
P248 练习
乙点的位置将移至丁点.
初试身手
2解:
观察相应变量区间的三个节律曲线的函数图象进行分析.
为了研究的方便,我们可以统一设A=10,
以出生日为自变量1,计算从出生日到本学期期末考试三天的天数得到三个自变量,
课堂小结
1.数学建模的步骤:
搜集数据,画散点图——观察散点图并进行函数拟合,选择函数模型——利用数据信息,求解函数模型.
2.利用三角函数模型解决实际问题的一般步骤:
3.利用函数模型解决实际问题需要注意,从数学模型中得到的答案还要根据实际情况检验它是否可行.
作业布置
t/s 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
y/cm -4.0 -2.8 0.0 2.8 4.0 2.8 0.0 -2.8 -4.0
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
