北京牛栏山第一中学2023-2024学年上学期高一10月月考数学试卷(PDF版,含解析)
文档属性
| 名称 | 北京牛栏山第一中学2023-2024学年上学期高一10月月考数学试卷(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 637.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 11:28:37 | ||
图片预览




文档简介
2023北京牛栏山一中高一 10月月考
数 学
(90 分钟) 2023.10
第一部分(填空题 共 42 分)
一、填空题共 14 小题,每小题 3 分,共 42 分,把答案填在答题卡相应位置上.
AB =
1. 如图,数轴上的两点 A,B,则 BA = ______; ______.
2. 若集合 A = 1,2,3 , B = 1,3,4 ,则 A B = ______, A B = ______.
2x 1 x2 2x 1
3. 已知分式方程 + = 5,令 = y ,化简可得关于 y 的整式方程为______.
2 2x 2x 1 x
4. 因式分解: ab 2a 2b + 4 = __________.
5. 若 x 1是 2x3 ax2 + 5x 1的一个因式,则a = ______.
1
6. 若 x2 2023x +1= 0 ,则 x + = ______.
x
a3
7. 化简 = ______.
a a
8. 不等式 x 2 1的解集为______.
9. 设 x, y R 2 2,满足方程 x + y =10x 6y 34,则 x + y = ______.
10. 已知集合M = 2,0,11 .若 A M ,且A 的元素中至少含有一个偶数,则满足条件的集合A 的个数为
______.
2
11. 在直角坐标系中将二次函数 y = 2(x 1) 2 的图像向左平移 1 个单位长度,再向上平移 1 个单位长
度,则所得抛物线的顶点坐标为______.
1 1 1 b a
12. 若 a,b R ,满足 = ,则 的值为______.
a b a +b a b
2
13. 若m2 = n + 2 , n = m+ 2(m n),则m+n = ______.
14. 某网店统计了连续三天售出商品的种类情况:第一天售出 19 种商品,第二天售出 13 种商品,第三天售
出 18 种商品;前两天都售出的商品有 3 种,后两天都售出的商品有 4 种,则该网店
①第一天售出但第二天未售出的商品有______种;
②这三天售出的商品最少有_______种.
第二部分(简答题 共 58 分)
第1页/共13页
二、解答题共 6 道题,共 58 分,解答应写出必要的文字说明,证明过程或演算步骤.
15. 设全集U = R ,集合 A = x | x 1 , B = x | x a .
(1)若 U A B ,求 a的取值范围;
(2)若 A B ,求 a的取值范围.
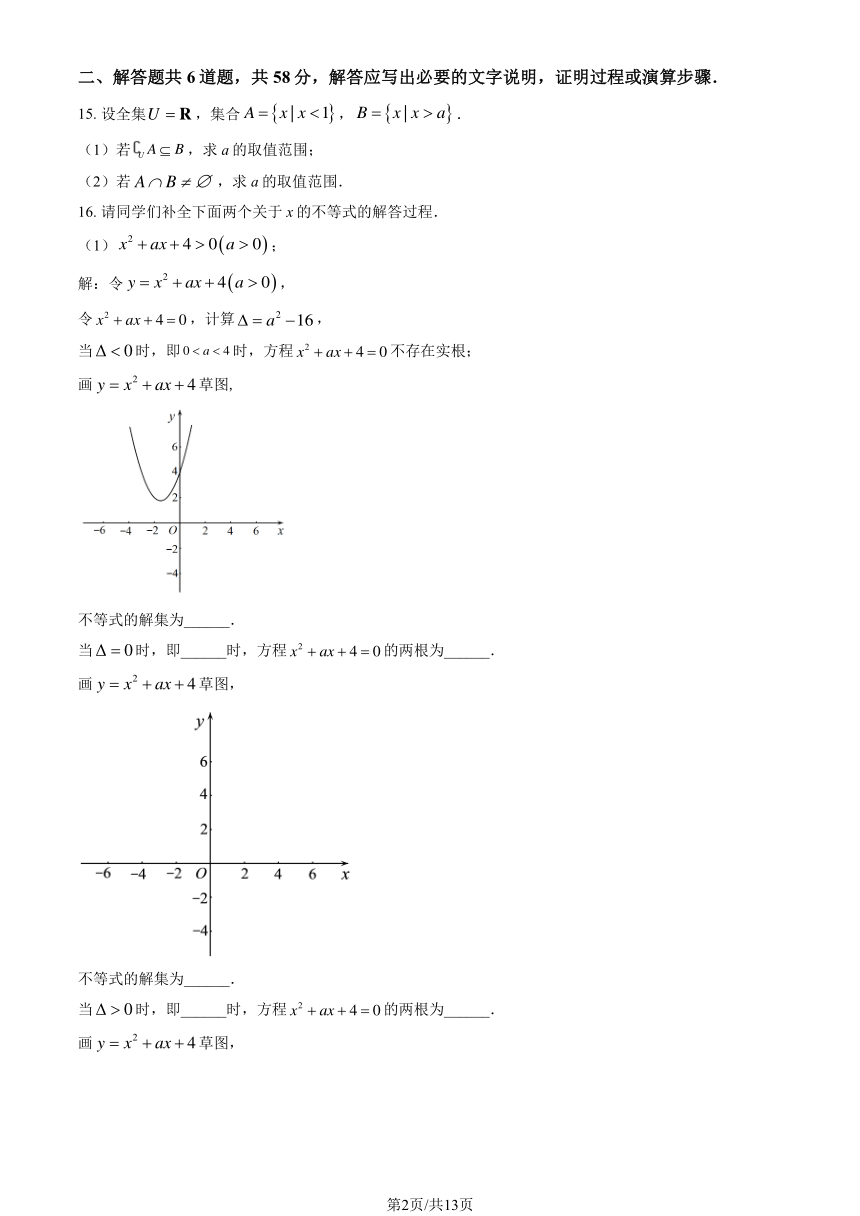
16. 请同学们补全下面两个关于 x的不等式的解答过程.
(1) x
2 + ax + 4 0(a 0);
2
解:令 y = x + ax + 4(a 0),
令 x2 + ax + 4 = 0,计算 = a2 16,
当Δ 0时,即 0 a 4 时,方程 x2 + ax + 4 = 0不存在实根;
画 y = x2 + ax + 4草图,
不等式的解集为______.
当Δ = 0时,即______时,方程 x2 + ax + 4 = 0的两根为______.
画 y = x2 + ax + 4草图,
不等式的解集为______.
当 0时,即______时,方程 x2 + ax + 4 = 0的两根为______.
2
画 y = x + ax + 4草图,
第2页/共13页
不等式的解集为______.
2
(2) x (x 6x +5) 0.
x (x2解:令 6x +5) = 0(*),
则方程(*)的三个根从小到大排列分别为 x1 = ______; x2 = ______; x3 = ______.
把三个根分别标在 x轴上,并完成表格,
x的取值范围 x x1 x1 x x2 x2 x x3 x x3
x (x2 6x + 5)的符号
请根据表格写出不等式 x (x2 6x +5) 0的解集.
17. 已知 A = x | x = 3k,k Z , B = x | x = 3k +1,k Z .
(1)判断 3,5 是否在集合 A中,并说明理由;
(2)判断6m 2(m Z)是否在集合 B中,并说明理由;
(3)若a A ,b B ,判断 a + b 是否属于集合 B,并说明理由.
x + y =1,
18. (1)解关于 x,y的方程组
x
2 y2 = 3.
x = x 1 x = x2 x
2 + 4y2 = 8,
(2)已知 和 是关于 x,y的方程组 (k为参数)的两组不同实数解.
y = y1 y = y2 y = k (x + 4).
2
32k 2 64k 8
求证:① x1 + x2 = ,2 x1x = ; 4k +1 2 4k 2 +1
② x1x2 +8+ 3x1 + 3x2 = 0;
第3页/共13页
x2 + 4 x1 + 4
③ = (其中 x1, x2 2 ). x2 + 2 x1 + 2
19. 证明:
(1)“ a 4 ”是“ x2 ax + 4 = 0 有两个不相等实数根”的充分不必要条件;
2
(2)设集合 A = x | 0 x 1 ,对集合 A中的每一个 x,不等式 ax bx 1均成立的一个必要不充分条
件为 a b +1.
20. 已知 A = (a1,a2 ,a3,a4 )为实数数组,定义集合
P (A) = a1,a2 ,a3,a4 ,a1 + a2 ,a2 + a3,a3 + a4 ,a1 + a2 + a3,a2 + a3 + a4 ,a1 + a2 + a3 + a4 ,给定正整数
m,若 1,2, ,m 1,m P (A),则称 A为m 连续生成数组.
(1)判断B = (0,2,1,4)是否为5 连续生成数组?是否为 6 连续生成数组?说明理由;
(2)若C = (0,1,a, 2)为 6 连续生成数组,求 a的值,并说明理由;
(3)数组 A = (a1,a2 ,a3,a4 )是否为10 连续生成数组?说明理由.
第4页/共13页
参考答案
第一部分(填空题 共 42 分)
一、填空题共 14 小题,每小题 3 分,共 42 分,把答案填在答题卡相应位置上.
1. 【答案】 ①. 2 ②. 2
【解析】
【分析】根据数轴上数的表示,及距离公式求解.
【详解】∵数轴上的两点 A,B对应的数分别是 1,3,
∴ BA =1 3 = 2 , AB = 3 1= 2.
故答案为: 2, 2 .
2. 【答案】 ①. 1, 2,3, 4 ②. 1,3
【解析】
【分析】根据并集、交集的定义求解.
【详解】集合 A = 1,2,3 , B = 1,3,4 ,则 A B = 1,2,3,4 , A B = 1,3 .
故答案为: 1, 2,3, 4 , 1,3 .
3. 【答案】 y2 5y +1= 0( y 1且 y 0 )
【解析】
2x 1
【分析】先考虑 = y 的范围 ,再代入分式方程,去分母化简整理可得答案.
x2
2
2x 1 1 2 1
【详解】∵ y = = + = 1 +1 1,( x =1时取等号),
x2 x2 x x
又由题意得 y 0 ,∴ y 1且 y 0 .
2x 1 2x 1 x2 1
将 = y ,代入
2 + = 5,得 y + = 5 , x x2 2x 1 y
化简整理可得关于 y 的整式方程为 y2 5y +1= 0( y 1且 y 0 ).
故答案为: y2 5y +1= 0( y 1且 y 0 ).
4. 【答案】 (a 2) (b 2)
【解析】
【分析】提取公因式即可分解因式.
【详解】 ab 2a 2b + 4 = a (b 2) 2(b 2) = (a 2) (b 2) .
故答案为: (a 2) (b 2) .
5. 【答案】6
第5页/共13页
【解析】
2 3 2
【分析】设多项式的另一个因式为 2x2 + bx + c,则 (x 1)(2x +bx + c) = 2x ax +5x 1,展开整
理,利用对应项系数相等即可求得 a,b,c 的值.
【详解】设多项式的另一个因式为 2x2 + bx + c,
则 (x 1)(2x2 +bx + c) = 2x3 ax2 +5x 1,
3
展开整理得, 2x + (b 2) x2 + (c b) x c = 2x3 ax2 + 5x 1,
b 2 = a
所以 c b = 5 ,解得 a = 6,b = 4,c =1 .
c = 1
故答案为:6.
6. 【答案】 2023
【解析】
【分析】整理方程,将目标式子化简即可求解.
【详解】因为 x2 2023x +1= 0 ,所以 x2 +1= 2023x,
1 x2 +1 2023x
所以 x + = = = 2023 .
x x x
故答案为: 2023 .
7. 【答案】 1
【解析】
【分析】将根式化成指数幂,再根据指数幂的运算法则计算.
3 3
a3 ( a)2 ( a)2
【详解】 = = = 1 . 1 3
a a ( a) ( a)2 ( a)2
故答案为: 1 .
8. 【答案】 (1,3)
【解析】
【分析】利用绝对值不等式的解法求解.
【详解】由 x 2 1得 1 x 2 1,解得1 x 3,
故不等式 x 2 1的解集为 (1,3) .
故答案为: (1,3) .
9. 【答案】2
【解析】
【分析】利用完全平方公式和非负数的性质求得 x, y 的值,然后代入求值即可.
第6页/共13页
【详解】∵ x2 + y2 =10x 6y 34,
∴ x2 + y2 10x + 6y + 34 = 0
∴ 2. (x 10x + 25) + (y2 + 6y + 9) = 0,
∴ (x 5)2 + (y + 3)2 = 0,
∴ x = 5, y = 3,
∴ x + y = 5+ ( 3) = 2 .
故答案为:2.
10. 【答案】5
【解析】
【详解】满足条件的集合A 有 2 、 0 、 2,0 、 2,11 、 0,11 .共 5 个.
故答案为 5
11. 【答案】 (0, 1)
【解析】
【分析】首先得到平移后的函数解析式,从而求出其顶点坐标.
2
【详解】将二次函数 y = 2(x 1) 2的图像向左平移 1 个单位长度,再向上平移 1 个单位长度得到
2
y = 2 (x +1) 1 2+1,
即 y = 2x2 1,
所以函数的顶点坐标为 (0, 1) .
故答案为: (0, 1)
12. 【答案】1
【解析】
【分析】对已知方程等价变形即可求解.
1 1 1 a + b a +b b a b a
【详解】因为 = ,所以 =1,所以 1+ 1+ =1,所以 =1.
a b a +b a b a b a b
故答案为:1 .
13.【答案】 1
【解析】
【分析】两式作差,利用平方差公式求解.
【详解】∵m n,∴m n 0,
若m2 = n + 2 , n2 = m + 2 ,
2
两式作差得m n
2 = n + 2 (m+ 2),即 (m + n)(m n) = n m,
第7页/共13页
两边同时除以m n得:m + n = 1.
故答案为: 1.
14. 【答案】 ①. 16; ②. 29
【解析】
【详解】试题分析:①设第一天售出商品的种类集为 A,第二天售出商品的种类集为 B,第三天售出商品
的种类集为 C,
如图,
则第一天售出但第二天未售出的商品有 19﹣3=16 种;
②由①知,前两天售出的商品种类为 19+13﹣3=29 种,第三天售出但第二天未售出的商品有 18﹣4=
14 种,当这 14 种
商品第一天售出但第二天未售出的 16 种商品中时,即第三天没有售出前两天的商品时,这三天售出的
商品种类最少为 29 种.
故答案为①16;②29.
【名师点睛】
本题将统计与实际情况相结合,创新味十足,是能力立意的好题,关键在于分析商品出售的所有可能的
情况,分类讨论时要做到不重复、不遗漏,另外,注意数形结合思想的运用.
第二部分(简答题 共 58 分)
二、解答题共 6 道题,共 58 分,解答应写出必要的文字说明,证明过程或演算步骤.
15. 【答案】(1)a 1
(2)a 1
【解析】
【分析】(1)由补集定义可得 U A ,由包含关系可得 a的范围;
(2)根据交集的定义可直接求得结果.
【小问 1 详解】
A = x | x 1 ,则 U A = x | x 1 ,
又 B = x | x a , U A B ,所以a 1.
【小问 2 详解】
A = x | x 1 , B = x | x a ,
若 A B ,则a 1.
16. 【答案】(1)答案见解析
(2)答案见解析
【解析】
【分析】(1)结合判别式,根据一元二次方程和二次函数,一元二次不等式的关系求解;
第8页/共13页
(2)根据方程的根与不等式解集的关系求解.
【小问 1 详解】
2
令 y = x + ax + 4(a 0),
令 x2 + ax + 4 = 0,计算 = a2 16,
当Δ 0时,即 20 a 4 时,方程 x2 + ax + 4 = 0不存在实根;画 y = x + ax + 4草图,
不等式的解集为R .
当Δ = 0时,即 a = 4时,方程 2x2 + ax + 4 = 0的两根为 x1 = x2 = 2.画 y = x + ax + 4草图,
不等式的解集为 x | x 2 .
a a2 16 a + a2 16
当 0时,即 a 4时,方程 x2 + ax + 4 = 0的两根为 x1 = , x2 = .
2 2
画 y = x2 + ax + 4草图,
第9页/共13页
a a
2 16 a + a2 16
不等式的解集为 x x 或 x .
2 2
【小问 2 详解】
x (x2令 6x +5) = 0(*),
则方程(*)的三个根从小到大排列分别为 x1 = 0; x2 = 1; x3 = 5.
把三个根分别标在 x轴上,
2
x 0 时, x2 6x + 5 0 ,则 x (x 6x +5) 0,
0 x 1时, x2 6x + 5 0 ,则 x (x2 6x +5) 0,
2
1 x 5时, x2 6x + 5 0,则 x (x 6x +5) 0,
x 5时, x2 6x + 5 0 ,则 x (x2 6x +5) 0,
完成表格,
x的取值范围 x x1 x1 x x2 x2 x x3 x x3
x (x2 6x + 5)的符号 - + - +
2
根据表格可得,不等式 x (x 6x +5) 0的解集为{x | x 0 或1 x 5}.
17. 【答案】(1)3 在集合 A中,5 不在集合 A中,理由见解析
(2)6m 2(m Z)在集合 B中,理由见解析
(3) a + b 属于集合 B ,理由见解析
【分析】(1)根据集合 A中元素的特征判断求解;
(2)根据集合 B 中元素的特征判断求解;
第10页/共13页
(3)设 a = 3p, p Z,b = 3q +1,q Z ,进而根据集合 B 中元素的特征判断求解.
【小问 1 详解】
∵3 = 3 1,∴3 在集合 A中,
5
令3k = 5,则 k = Z,故 5 不在集合 A中.
3
【小问 2 详解】
6m 2 = 3(2m 1)+1,且 2m 1 Z ,故6m 2(m Z)在集合 B中.
【小问 3 详解】
设 a = 3p, p Z,b = 3q +1,q Z ,
则 a +b = 3( p + q)+1, p + q Z ,
所以 a + b 属于集合 B .
18. 【答案】(1) (2, 1) ,(2)证明见解析
【分析】(1)利用代入消元法求解即可;
(2)由方程组消元得一元二次方程,结合韦达定理证明即可.
x + y =1
【详解】(1)由方程组 ,消元得 2x 4 = 0,解得 x = 2 ,从而 y =1 2 = 1, 2 2
x y = 3
∴方程组的解为 (2, 1) .
2 2
x + 4y = 8 (4k 2(2)由方程组 ,消元得 +1) x2 +32k 2x + 64k 2 8 = 0(*),
y = k (x + 4)
由题意, x1, x2 是此方程(*)的两个不同实根,
2
则 = (32k 2
1 1
) 4(4k 2 +1)(64k 2 8) 0 ,得16k 2 1 0 ,即 k ,
4 4
32k 2 64k 2 8
①由韦达定理得 x1 + x2 = ,2 x x = ; 4k +1 1 2 4k 2 +1
64k 2 8 3( 32k 2 ) 64k 2 8+32k 2 +8 96k 2
② x1x2 +8+3x1 +3x = +8+ = = 0;
2
4k 2 +1 4k 2 +1 4k 2 +1
③∵ (x2 + 4)(x1 + 2)+ (x1 + 4)(x2 + 2) = 2 x1x2 +3(x1 + x2 )+8 = 2 0 = 0,
x2 + 4 x + 4
∵ x + 2 0, x + 2 0,∴ =
1
1 2 .
x2 + 2 x1 + 2
19. 【答案】(1)证明见解析
(2)证明见解析
【分析】(1)利用充分条件与必要条件的概念,结合方程的判别式证明;
(2)利用充分条件与必要条件的概念,结合特值法证明.
第11页/共13页
【小问 1 详解】
x2 ax + 4 = 0 有两个不相等实数根 = a2 4 4 0 a 4或 a 4 .
“ a 4 ”可以推出“ a 4或 a 4 ”, “ a 4或 a 4 ”不能推出“ a 4 ”,
所以“ a 4 ”是“ x2 ax + 4 = 0 有两个不相等实数根”的充分不必要条件.
【小问 2 详解】
若对集合 A = x | 0 x 1 x 2中的每一个 ,不等式 ax bx 1均成立,
令 x =1得 a b 1,∴ 1 a b 1,∴b 1 a b +1,从而 a b +1成立.
2 2
若 a b +1,取 a = 1,b =1,则 ax bx 1可化为 x + x 1,
2
当 x =1时,满足0 x 1,但 x + x = 2 1 ax bx
2
,即不等式 1不成立.
综上,设集合 A = x | 0 x 1 ,对集合 A中的每一个 x,不等式 ax bx2 1均成立的一个必要不充分
条件为 a b +1.
20. 【答案】(1)B = (0,2,1,4)是5 连续生成数组,不是 6 连续生成数组,理由见解析
(2) a = 3 ,理由见解析
(3)数组 A = (a1,a2 ,a3,a4 )不是10 连续生成数组,理由见解析
【分析】(1)根据m 连续生成数组的定义,结合子集的概念求解;
(2)根据题意,得出 P (C )中元素的可能取值,结合子集的概念求解;
(3)根据题意 P (A) = 1,2,3,4,5,6,7,8,9,10 ,从而 a1,a2 ,a3,a4 1,2,3,4,5,6,7,8,9,10 ,集合
P (A) , 1,2,3,4,5,6,7,8,9,10 中元素求和可得 4(a1 + a4 ) + 6(a2 + a3) = 55,进而可得出答案.
【小问 1 详解】
B = (0,2,1,4), P (B) = 0,1,2,3,4,5,7 ,
∵ 1,2,3,4,5 P (B),∴ B = (0,2,1,4)是5 连续生成数组,
∵ 1,2,3,4,5,6 不是 P (B)的子集,∴ B = (0,2,1,4)不是 6 连续生成数组.
【小问 2 详解】
C = (0,1,a, 2), P (C )中元素可能取值为0,1,2,a,a +1,a + 2,a +3,
若C = (0,1,a, 2)为 6 连续生成数组,即 1,2,3,4,5,6 P (C ),
则 a = 3 .
【小问 3 详解】
若 A = (a1,a2 ,a3,a4 )为10 连续生成数组,则 1,2,3,4,5,6,7,8,9,10 P (A),
又 P (A) = a1,a2 ,a3,a4 ,a1 + a2 ,a2 + a3,a3 + a4 ,a1 + a2 + a3,a2 + a3 + a4 ,a1 + a2 + a3 + a4 中最多有 10 个
元素,
第12页/共13页
则 P (A) = 1,2,3,4,5,6,7,8,9,10 ,从而a1,a2 ,a3,a4 1,2,3,4,5,6,7,8,9,10 ,
∴ a1 + a2 + a3 + a4 + (a1 + a2 )+ (a2 + a3)+ (a3 + a4 )+ (a1 + a2 + a3)+ (a2 + a3 + a4 )
+(a1 + a2 + a3 + a4 ) =1+ 2+ 3+ 4+ 5+ 6+ 7 +8+9+10 ,
即 4(a1 + a4 ) + 6(a2 + a3) = 55,
∵ a1,a2 ,a3,a4 1,2,3,4,5,6,7,8,9,10 ,∴ 4(a1 + a4 ) + 6(a2 + a3)为偶数,
而 55 为奇数,4(a1 + a4 ) + 6(a2 + a3) = 55不能成立,
∴数组 A = (a1,a2 ,a3,a4 )不是10 连续生成数组.
第13页/共13页
数 学
(90 分钟) 2023.10
第一部分(填空题 共 42 分)
一、填空题共 14 小题,每小题 3 分,共 42 分,把答案填在答题卡相应位置上.
AB =
1. 如图,数轴上的两点 A,B,则 BA = ______; ______.
2. 若集合 A = 1,2,3 , B = 1,3,4 ,则 A B = ______, A B = ______.
2x 1 x2 2x 1
3. 已知分式方程 + = 5,令 = y ,化简可得关于 y 的整式方程为______.
2 2x 2x 1 x
4. 因式分解: ab 2a 2b + 4 = __________.
5. 若 x 1是 2x3 ax2 + 5x 1的一个因式,则a = ______.
1
6. 若 x2 2023x +1= 0 ,则 x + = ______.
x
a3
7. 化简 = ______.
a a
8. 不等式 x 2 1的解集为______.
9. 设 x, y R 2 2,满足方程 x + y =10x 6y 34,则 x + y = ______.
10. 已知集合M = 2,0,11 .若 A M ,且A 的元素中至少含有一个偶数,则满足条件的集合A 的个数为
______.
2
11. 在直角坐标系中将二次函数 y = 2(x 1) 2 的图像向左平移 1 个单位长度,再向上平移 1 个单位长
度,则所得抛物线的顶点坐标为______.
1 1 1 b a
12. 若 a,b R ,满足 = ,则 的值为______.
a b a +b a b
2
13. 若m2 = n + 2 , n = m+ 2(m n),则m+n = ______.
14. 某网店统计了连续三天售出商品的种类情况:第一天售出 19 种商品,第二天售出 13 种商品,第三天售
出 18 种商品;前两天都售出的商品有 3 种,后两天都售出的商品有 4 种,则该网店
①第一天售出但第二天未售出的商品有______种;
②这三天售出的商品最少有_______种.
第二部分(简答题 共 58 分)
第1页/共13页
二、解答题共 6 道题,共 58 分,解答应写出必要的文字说明,证明过程或演算步骤.
15. 设全集U = R ,集合 A = x | x 1 , B = x | x a .
(1)若 U A B ,求 a的取值范围;
(2)若 A B ,求 a的取值范围.
16. 请同学们补全下面两个关于 x的不等式的解答过程.
(1) x
2 + ax + 4 0(a 0);
2
解:令 y = x + ax + 4(a 0),
令 x2 + ax + 4 = 0,计算 = a2 16,
当Δ 0时,即 0 a 4 时,方程 x2 + ax + 4 = 0不存在实根;
画 y = x2 + ax + 4草图,
不等式的解集为______.
当Δ = 0时,即______时,方程 x2 + ax + 4 = 0的两根为______.
画 y = x2 + ax + 4草图,
不等式的解集为______.
当 0时,即______时,方程 x2 + ax + 4 = 0的两根为______.
2
画 y = x + ax + 4草图,
第2页/共13页
不等式的解集为______.
2
(2) x (x 6x +5) 0.
x (x2解:令 6x +5) = 0(*),
则方程(*)的三个根从小到大排列分别为 x1 = ______; x2 = ______; x3 = ______.
把三个根分别标在 x轴上,并完成表格,
x的取值范围 x x1 x1 x x2 x2 x x3 x x3
x (x2 6x + 5)的符号
请根据表格写出不等式 x (x2 6x +5) 0的解集.
17. 已知 A = x | x = 3k,k Z , B = x | x = 3k +1,k Z .
(1)判断 3,5 是否在集合 A中,并说明理由;
(2)判断6m 2(m Z)是否在集合 B中,并说明理由;
(3)若a A ,b B ,判断 a + b 是否属于集合 B,并说明理由.
x + y =1,
18. (1)解关于 x,y的方程组
x
2 y2 = 3.
x = x 1 x = x2 x
2 + 4y2 = 8,
(2)已知 和 是关于 x,y的方程组 (k为参数)的两组不同实数解.
y = y1 y = y2 y = k (x + 4).
2
32k 2 64k 8
求证:① x1 + x2 = ,2 x1x = ; 4k +1 2 4k 2 +1
② x1x2 +8+ 3x1 + 3x2 = 0;
第3页/共13页
x2 + 4 x1 + 4
③ = (其中 x1, x2 2 ). x2 + 2 x1 + 2
19. 证明:
(1)“ a 4 ”是“ x2 ax + 4 = 0 有两个不相等实数根”的充分不必要条件;
2
(2)设集合 A = x | 0 x 1 ,对集合 A中的每一个 x,不等式 ax bx 1均成立的一个必要不充分条
件为 a b +1.
20. 已知 A = (a1,a2 ,a3,a4 )为实数数组,定义集合
P (A) = a1,a2 ,a3,a4 ,a1 + a2 ,a2 + a3,a3 + a4 ,a1 + a2 + a3,a2 + a3 + a4 ,a1 + a2 + a3 + a4 ,给定正整数
m,若 1,2, ,m 1,m P (A),则称 A为m 连续生成数组.
(1)判断B = (0,2,1,4)是否为5 连续生成数组?是否为 6 连续生成数组?说明理由;
(2)若C = (0,1,a, 2)为 6 连续生成数组,求 a的值,并说明理由;
(3)数组 A = (a1,a2 ,a3,a4 )是否为10 连续生成数组?说明理由.
第4页/共13页
参考答案
第一部分(填空题 共 42 分)
一、填空题共 14 小题,每小题 3 分,共 42 分,把答案填在答题卡相应位置上.
1. 【答案】 ①. 2 ②. 2
【解析】
【分析】根据数轴上数的表示,及距离公式求解.
【详解】∵数轴上的两点 A,B对应的数分别是 1,3,
∴ BA =1 3 = 2 , AB = 3 1= 2.
故答案为: 2, 2 .
2. 【答案】 ①. 1, 2,3, 4 ②. 1,3
【解析】
【分析】根据并集、交集的定义求解.
【详解】集合 A = 1,2,3 , B = 1,3,4 ,则 A B = 1,2,3,4 , A B = 1,3 .
故答案为: 1, 2,3, 4 , 1,3 .
3. 【答案】 y2 5y +1= 0( y 1且 y 0 )
【解析】
2x 1
【分析】先考虑 = y 的范围 ,再代入分式方程,去分母化简整理可得答案.
x2
2
2x 1 1 2 1
【详解】∵ y = = + = 1 +1 1,( x =1时取等号),
x2 x2 x x
又由题意得 y 0 ,∴ y 1且 y 0 .
2x 1 2x 1 x2 1
将 = y ,代入
2 + = 5,得 y + = 5 , x x2 2x 1 y
化简整理可得关于 y 的整式方程为 y2 5y +1= 0( y 1且 y 0 ).
故答案为: y2 5y +1= 0( y 1且 y 0 ).
4. 【答案】 (a 2) (b 2)
【解析】
【分析】提取公因式即可分解因式.
【详解】 ab 2a 2b + 4 = a (b 2) 2(b 2) = (a 2) (b 2) .
故答案为: (a 2) (b 2) .
5. 【答案】6
第5页/共13页
【解析】
2 3 2
【分析】设多项式的另一个因式为 2x2 + bx + c,则 (x 1)(2x +bx + c) = 2x ax +5x 1,展开整
理,利用对应项系数相等即可求得 a,b,c 的值.
【详解】设多项式的另一个因式为 2x2 + bx + c,
则 (x 1)(2x2 +bx + c) = 2x3 ax2 +5x 1,
3
展开整理得, 2x + (b 2) x2 + (c b) x c = 2x3 ax2 + 5x 1,
b 2 = a
所以 c b = 5 ,解得 a = 6,b = 4,c =1 .
c = 1
故答案为:6.
6. 【答案】 2023
【解析】
【分析】整理方程,将目标式子化简即可求解.
【详解】因为 x2 2023x +1= 0 ,所以 x2 +1= 2023x,
1 x2 +1 2023x
所以 x + = = = 2023 .
x x x
故答案为: 2023 .
7. 【答案】 1
【解析】
【分析】将根式化成指数幂,再根据指数幂的运算法则计算.
3 3
a3 ( a)2 ( a)2
【详解】 = = = 1 . 1 3
a a ( a) ( a)2 ( a)2
故答案为: 1 .
8. 【答案】 (1,3)
【解析】
【分析】利用绝对值不等式的解法求解.
【详解】由 x 2 1得 1 x 2 1,解得1 x 3,
故不等式 x 2 1的解集为 (1,3) .
故答案为: (1,3) .
9. 【答案】2
【解析】
【分析】利用完全平方公式和非负数的性质求得 x, y 的值,然后代入求值即可.
第6页/共13页
【详解】∵ x2 + y2 =10x 6y 34,
∴ x2 + y2 10x + 6y + 34 = 0
∴ 2. (x 10x + 25) + (y2 + 6y + 9) = 0,
∴ (x 5)2 + (y + 3)2 = 0,
∴ x = 5, y = 3,
∴ x + y = 5+ ( 3) = 2 .
故答案为:2.
10. 【答案】5
【解析】
【详解】满足条件的集合A 有 2 、 0 、 2,0 、 2,11 、 0,11 .共 5 个.
故答案为 5
11. 【答案】 (0, 1)
【解析】
【分析】首先得到平移后的函数解析式,从而求出其顶点坐标.
2
【详解】将二次函数 y = 2(x 1) 2的图像向左平移 1 个单位长度,再向上平移 1 个单位长度得到
2
y = 2 (x +1) 1 2+1,
即 y = 2x2 1,
所以函数的顶点坐标为 (0, 1) .
故答案为: (0, 1)
12. 【答案】1
【解析】
【分析】对已知方程等价变形即可求解.
1 1 1 a + b a +b b a b a
【详解】因为 = ,所以 =1,所以 1+ 1+ =1,所以 =1.
a b a +b a b a b a b
故答案为:1 .
13.【答案】 1
【解析】
【分析】两式作差,利用平方差公式求解.
【详解】∵m n,∴m n 0,
若m2 = n + 2 , n2 = m + 2 ,
2
两式作差得m n
2 = n + 2 (m+ 2),即 (m + n)(m n) = n m,
第7页/共13页
两边同时除以m n得:m + n = 1.
故答案为: 1.
14. 【答案】 ①. 16; ②. 29
【解析】
【详解】试题分析:①设第一天售出商品的种类集为 A,第二天售出商品的种类集为 B,第三天售出商品
的种类集为 C,
如图,
则第一天售出但第二天未售出的商品有 19﹣3=16 种;
②由①知,前两天售出的商品种类为 19+13﹣3=29 种,第三天售出但第二天未售出的商品有 18﹣4=
14 种,当这 14 种
商品第一天售出但第二天未售出的 16 种商品中时,即第三天没有售出前两天的商品时,这三天售出的
商品种类最少为 29 种.
故答案为①16;②29.
【名师点睛】
本题将统计与实际情况相结合,创新味十足,是能力立意的好题,关键在于分析商品出售的所有可能的
情况,分类讨论时要做到不重复、不遗漏,另外,注意数形结合思想的运用.
第二部分(简答题 共 58 分)
二、解答题共 6 道题,共 58 分,解答应写出必要的文字说明,证明过程或演算步骤.
15. 【答案】(1)a 1
(2)a 1
【解析】
【分析】(1)由补集定义可得 U A ,由包含关系可得 a的范围;
(2)根据交集的定义可直接求得结果.
【小问 1 详解】
A = x | x 1 ,则 U A = x | x 1 ,
又 B = x | x a , U A B ,所以a 1.
【小问 2 详解】
A = x | x 1 , B = x | x a ,
若 A B ,则a 1.
16. 【答案】(1)答案见解析
(2)答案见解析
【解析】
【分析】(1)结合判别式,根据一元二次方程和二次函数,一元二次不等式的关系求解;
第8页/共13页
(2)根据方程的根与不等式解集的关系求解.
【小问 1 详解】
2
令 y = x + ax + 4(a 0),
令 x2 + ax + 4 = 0,计算 = a2 16,
当Δ 0时,即 20 a 4 时,方程 x2 + ax + 4 = 0不存在实根;画 y = x + ax + 4草图,
不等式的解集为R .
当Δ = 0时,即 a = 4时,方程 2x2 + ax + 4 = 0的两根为 x1 = x2 = 2.画 y = x + ax + 4草图,
不等式的解集为 x | x 2 .
a a2 16 a + a2 16
当 0时,即 a 4时,方程 x2 + ax + 4 = 0的两根为 x1 = , x2 = .
2 2
画 y = x2 + ax + 4草图,
第9页/共13页
a a
2 16 a + a2 16
不等式的解集为 x x 或 x .
2 2
【小问 2 详解】
x (x2令 6x +5) = 0(*),
则方程(*)的三个根从小到大排列分别为 x1 = 0; x2 = 1; x3 = 5.
把三个根分别标在 x轴上,
2
x 0 时, x2 6x + 5 0 ,则 x (x 6x +5) 0,
0 x 1时, x2 6x + 5 0 ,则 x (x2 6x +5) 0,
2
1 x 5时, x2 6x + 5 0,则 x (x 6x +5) 0,
x 5时, x2 6x + 5 0 ,则 x (x2 6x +5) 0,
完成表格,
x的取值范围 x x1 x1 x x2 x2 x x3 x x3
x (x2 6x + 5)的符号 - + - +
2
根据表格可得,不等式 x (x 6x +5) 0的解集为{x | x 0 或1 x 5}.
17. 【答案】(1)3 在集合 A中,5 不在集合 A中,理由见解析
(2)6m 2(m Z)在集合 B中,理由见解析
(3) a + b 属于集合 B ,理由见解析
【分析】(1)根据集合 A中元素的特征判断求解;
(2)根据集合 B 中元素的特征判断求解;
第10页/共13页
(3)设 a = 3p, p Z,b = 3q +1,q Z ,进而根据集合 B 中元素的特征判断求解.
【小问 1 详解】
∵3 = 3 1,∴3 在集合 A中,
5
令3k = 5,则 k = Z,故 5 不在集合 A中.
3
【小问 2 详解】
6m 2 = 3(2m 1)+1,且 2m 1 Z ,故6m 2(m Z)在集合 B中.
【小问 3 详解】
设 a = 3p, p Z,b = 3q +1,q Z ,
则 a +b = 3( p + q)+1, p + q Z ,
所以 a + b 属于集合 B .
18. 【答案】(1) (2, 1) ,(2)证明见解析
【分析】(1)利用代入消元法求解即可;
(2)由方程组消元得一元二次方程,结合韦达定理证明即可.
x + y =1
【详解】(1)由方程组 ,消元得 2x 4 = 0,解得 x = 2 ,从而 y =1 2 = 1, 2 2
x y = 3
∴方程组的解为 (2, 1) .
2 2
x + 4y = 8 (4k 2(2)由方程组 ,消元得 +1) x2 +32k 2x + 64k 2 8 = 0(*),
y = k (x + 4)
由题意, x1, x2 是此方程(*)的两个不同实根,
2
则 = (32k 2
1 1
) 4(4k 2 +1)(64k 2 8) 0 ,得16k 2 1 0 ,即 k ,
4 4
32k 2 64k 2 8
①由韦达定理得 x1 + x2 = ,2 x x = ; 4k +1 1 2 4k 2 +1
64k 2 8 3( 32k 2 ) 64k 2 8+32k 2 +8 96k 2
② x1x2 +8+3x1 +3x = +8+ = = 0;
2
4k 2 +1 4k 2 +1 4k 2 +1
③∵ (x2 + 4)(x1 + 2)+ (x1 + 4)(x2 + 2) = 2 x1x2 +3(x1 + x2 )+8 = 2 0 = 0,
x2 + 4 x + 4
∵ x + 2 0, x + 2 0,∴ =
1
1 2 .
x2 + 2 x1 + 2
19. 【答案】(1)证明见解析
(2)证明见解析
【分析】(1)利用充分条件与必要条件的概念,结合方程的判别式证明;
(2)利用充分条件与必要条件的概念,结合特值法证明.
第11页/共13页
【小问 1 详解】
x2 ax + 4 = 0 有两个不相等实数根 = a2 4 4 0 a 4或 a 4 .
“ a 4 ”可以推出“ a 4或 a 4 ”, “ a 4或 a 4 ”不能推出“ a 4 ”,
所以“ a 4 ”是“ x2 ax + 4 = 0 有两个不相等实数根”的充分不必要条件.
【小问 2 详解】
若对集合 A = x | 0 x 1 x 2中的每一个 ,不等式 ax bx 1均成立,
令 x =1得 a b 1,∴ 1 a b 1,∴b 1 a b +1,从而 a b +1成立.
2 2
若 a b +1,取 a = 1,b =1,则 ax bx 1可化为 x + x 1,
2
当 x =1时,满足0 x 1,但 x + x = 2 1 ax bx
2
,即不等式 1不成立.
综上,设集合 A = x | 0 x 1 ,对集合 A中的每一个 x,不等式 ax bx2 1均成立的一个必要不充分
条件为 a b +1.
20. 【答案】(1)B = (0,2,1,4)是5 连续生成数组,不是 6 连续生成数组,理由见解析
(2) a = 3 ,理由见解析
(3)数组 A = (a1,a2 ,a3,a4 )不是10 连续生成数组,理由见解析
【分析】(1)根据m 连续生成数组的定义,结合子集的概念求解;
(2)根据题意,得出 P (C )中元素的可能取值,结合子集的概念求解;
(3)根据题意 P (A) = 1,2,3,4,5,6,7,8,9,10 ,从而 a1,a2 ,a3,a4 1,2,3,4,5,6,7,8,9,10 ,集合
P (A) , 1,2,3,4,5,6,7,8,9,10 中元素求和可得 4(a1 + a4 ) + 6(a2 + a3) = 55,进而可得出答案.
【小问 1 详解】
B = (0,2,1,4), P (B) = 0,1,2,3,4,5,7 ,
∵ 1,2,3,4,5 P (B),∴ B = (0,2,1,4)是5 连续生成数组,
∵ 1,2,3,4,5,6 不是 P (B)的子集,∴ B = (0,2,1,4)不是 6 连续生成数组.
【小问 2 详解】
C = (0,1,a, 2), P (C )中元素可能取值为0,1,2,a,a +1,a + 2,a +3,
若C = (0,1,a, 2)为 6 连续生成数组,即 1,2,3,4,5,6 P (C ),
则 a = 3 .
【小问 3 详解】
若 A = (a1,a2 ,a3,a4 )为10 连续生成数组,则 1,2,3,4,5,6,7,8,9,10 P (A),
又 P (A) = a1,a2 ,a3,a4 ,a1 + a2 ,a2 + a3,a3 + a4 ,a1 + a2 + a3,a2 + a3 + a4 ,a1 + a2 + a3 + a4 中最多有 10 个
元素,
第12页/共13页
则 P (A) = 1,2,3,4,5,6,7,8,9,10 ,从而a1,a2 ,a3,a4 1,2,3,4,5,6,7,8,9,10 ,
∴ a1 + a2 + a3 + a4 + (a1 + a2 )+ (a2 + a3)+ (a3 + a4 )+ (a1 + a2 + a3)+ (a2 + a3 + a4 )
+(a1 + a2 + a3 + a4 ) =1+ 2+ 3+ 4+ 5+ 6+ 7 +8+9+10 ,
即 4(a1 + a4 ) + 6(a2 + a3) = 55,
∵ a1,a2 ,a3,a4 1,2,3,4,5,6,7,8,9,10 ,∴ 4(a1 + a4 ) + 6(a2 + a3)为偶数,
而 55 为奇数,4(a1 + a4 ) + 6(a2 + a3) = 55不能成立,
∴数组 A = (a1,a2 ,a3,a4 )不是10 连续生成数组.
第13页/共13页
同课章节目录
