必修2第2章直线与平面平行的判定(湖南省邵阳市武冈市)
文档属性
| 名称 | 必修2第2章直线与平面平行的判定(湖南省邵阳市武冈市) |  | |
| 格式 | rar | ||
| 文件大小 | 743.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-02 22:53:00 | ||
图片预览





文档简介
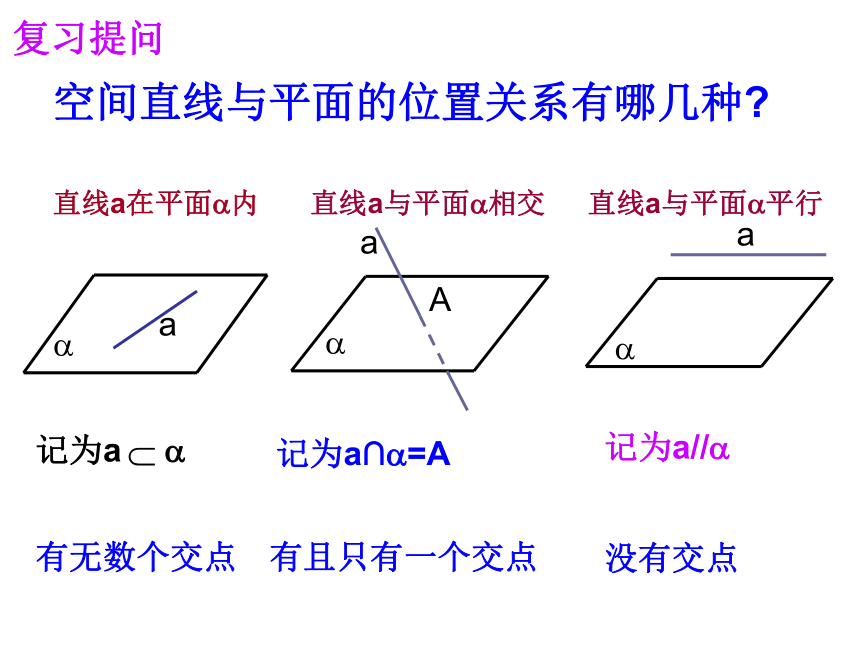
课件19张PPT。直线与平面平行的判定教学目标:理解并掌握直线与平面平行的判定定理;并会用判定定理证明直线与平面 平行。引课:我们已经学习过空间点、直线、平面之间的位置关系,在这些关系中,直线和平面、平面和平面的关系最为重要。今天我们要来学习的是:直线和平面平行的判定。直线a在平面?内直线a与平面?相交记为a∩?=A记为a//?
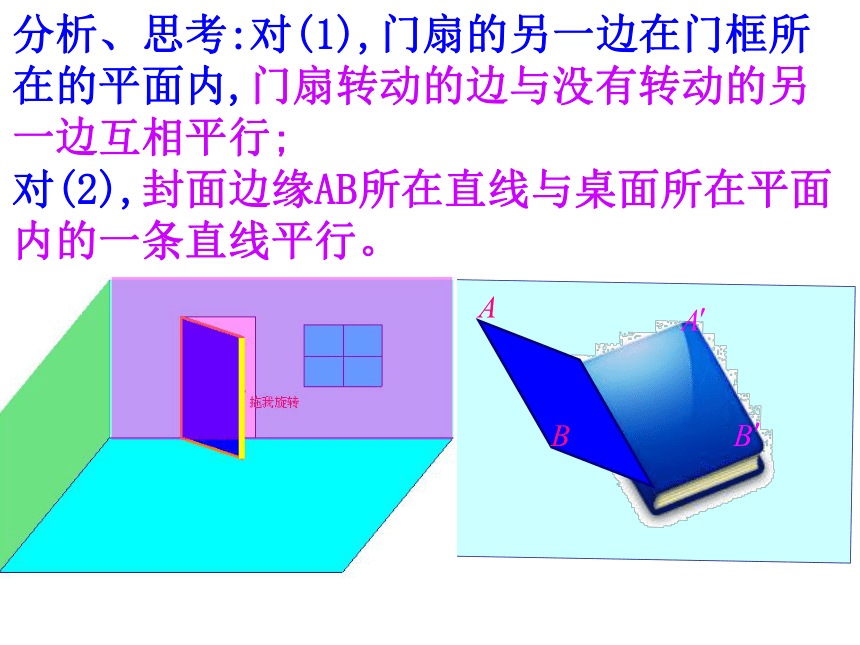
有无数个交点有且只有一个交点没有交点空间直线与平面的位置关系有哪几种?复习提问直线a与平面?平行提出问题:在直线与平面的位置关系中,平行是一种非常重要的关系。它不仅应用较多,而且是学习平面与平面平行的基础。怎样判断直线与平面平行呢?答:用定义法判断,只须判定直线和平面有没有公共点。指出:这个方法好是好,但并不实用。因为直线无限伸展,平面无限延展;此处无交点并不表示延伸后就没有交点。我们还是先来看看:1、生活中线面平行的例子(1) 门扇的两边是平行的,当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象。(2)??观察:如图,将一本书平放桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系? 分析、思考:对(1),门扇的另一边在门框所在的平面内,门扇转动的边与没有转动的另一边互相平行;
对(2),封面边缘AB所在直线与桌面所在平面内的一条直线平行。猜想、证明:是不是只要平面外的一条直线和平面内的一条直线平行,就能推出这条直线和平面平行呢?观察(1)这两条直线共面吗?探究直线与平面平行共面不可能相交抽象概括直线与平面平行的判定定理: 若平面外一条直线与此平面内的一条直线平行,
则该直线与此平面平行. 仔细分析下,判定定理告诉我们,判定直线与平面平行的条件有几个,是什么?
定理中必须的条件有三个,分别为:a与b平行,即a∥b(平行)用符号语言可概括为:简述为:线线平行?线面平行对判定定理的再认识:它是证明直线与平面平行最常用最简易的方法;应用定理时,应注意三个条件是缺一不可的;要证明直线与平面平行,只要在这个平面内找出一条直线与已知直线平行,把证明线面问题转化为证明线线问题.例题示范,巩固新知:例1 求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面.已知:空间四边形ABCD中,E,F分别AB,AD的中点.求证:EF//平面BCD.证明:连接BD.因为 AE=EB,AF=FD,
所以 EF//BD(三角形中位线的性质) 1.如图,长方体 中, (1)与AB平行的平面是 ;(2)与 平行的平面是 ;(3)与AD平行的平面是 ;练一练,巩固新知:P55练习1题证明:连接BD交AC于点O,连接OE,练一练,巩固新知:P55练习2题补充练习:判断对错直线a与平面α不平行,即a与平面α?相交.(?)直线a∥b,直线b 平面α,则直线a∥平面α.(?) 直线a∥平面α,直线b 平面α,则直线a∥b.(?)
C1ACB1BMNA1如图,三棱柱ABC-A1B1C1中,M、 N分别是BC和A1B1的中点,求证:MN∥平面AA1C1CF证明:设A1C1中点为F,连结NF,FC.∵N为A1B1中点,M是BC的中点,∴NFCM为平行四边形,故MN∥CF∴ MN∥平面AA1C1C,补充练习:小结:1.直线与平面平行的判定:2.应用判定定理时,应当注意三个 不可或缺的条件,即:a与b平行,即a∥b(平行)作业:
1、教材第61页?习题2.2?A组第3题;
2、预习:如何判定两个平面平行?
有无数个交点有且只有一个交点没有交点空间直线与平面的位置关系有哪几种?复习提问直线a与平面?平行提出问题:在直线与平面的位置关系中,平行是一种非常重要的关系。它不仅应用较多,而且是学习平面与平面平行的基础。怎样判断直线与平面平行呢?答:用定义法判断,只须判定直线和平面有没有公共点。指出:这个方法好是好,但并不实用。因为直线无限伸展,平面无限延展;此处无交点并不表示延伸后就没有交点。我们还是先来看看:1、生活中线面平行的例子(1) 门扇的两边是平行的,当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象。(2)??观察:如图,将一本书平放桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系? 分析、思考:对(1),门扇的另一边在门框所在的平面内,门扇转动的边与没有转动的另一边互相平行;
对(2),封面边缘AB所在直线与桌面所在平面内的一条直线平行。猜想、证明:是不是只要平面外的一条直线和平面内的一条直线平行,就能推出这条直线和平面平行呢?观察(1)这两条直线共面吗?探究直线与平面平行共面不可能相交抽象概括直线与平面平行的判定定理: 若平面外一条直线与此平面内的一条直线平行,
则该直线与此平面平行. 仔细分析下,判定定理告诉我们,判定直线与平面平行的条件有几个,是什么?
定理中必须的条件有三个,分别为:a与b平行,即a∥b(平行)用符号语言可概括为:简述为:线线平行?线面平行对判定定理的再认识:它是证明直线与平面平行最常用最简易的方法;应用定理时,应注意三个条件是缺一不可的;要证明直线与平面平行,只要在这个平面内找出一条直线与已知直线平行,把证明线面问题转化为证明线线问题.例题示范,巩固新知:例1 求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面.已知:空间四边形ABCD中,E,F分别AB,AD的中点.求证:EF//平面BCD.证明:连接BD.因为 AE=EB,AF=FD,
所以 EF//BD(三角形中位线的性质) 1.如图,长方体 中, (1)与AB平行的平面是 ;(2)与 平行的平面是 ;(3)与AD平行的平面是 ;练一练,巩固新知:P55练习1题证明:连接BD交AC于点O,连接OE,练一练,巩固新知:P55练习2题补充练习:判断对错直线a与平面α不平行,即a与平面α?相交.(?)直线a∥b,直线b 平面α,则直线a∥平面α.(?) 直线a∥平面α,直线b 平面α,则直线a∥b.(?)
C1ACB1BMNA1如图,三棱柱ABC-A1B1C1中,M、 N分别是BC和A1B1的中点,求证:MN∥平面AA1C1CF证明:设A1C1中点为F,连结NF,FC.∵N为A1B1中点,M是BC的中点,∴NFCM为平行四边形,故MN∥CF∴ MN∥平面AA1C1C,补充练习:小结:1.直线与平面平行的判定:2.应用判定定理时,应当注意三个 不可或缺的条件,即:a与b平行,即a∥b(平行)作业:
1、教材第61页?习题2.2?A组第3题;
2、预习:如何判定两个平面平行?
