初中数学北师大版九年级下册第一章 1.6利用三角函数测高
文档属性
| 名称 | 初中数学北师大版九年级下册第一章 1.6利用三角函数测高 |

|
|
| 格式 | doc | ||
| 文件大小 | 482.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 14:02:57 | ||
图片预览

文档简介
利用三角函数测高 教学设计
北师大 科目 数学 年级 九年级 下 册
课题 1.6 利用三角函数测高
教学目标 会利用直角三角形的边角关系测物体的高度。
教学重点 会利用直角三角形的边角关系测物体的高度。
教学难点 理解直角三角形的边角关系的意义和与现实生活的联系.
教学方法 本节课教师采取了启发、引导、提问、点拨等教学方式,让学生在实践探究和思考中学习。
学法指导 学生通过自主学习、动手实践、交流讨论、学习展示等学法进行学习,同时对于同伴们的分享和老师的点拨及时倾听,内化为自己的东西。数学学习过程应该是大胆猜想—实践探究—案例验证—总结提升的过程
教具准备 数学课本 绩优学案 教师用书
教学过程 问题设置 师生活动
情景引入 展示图片,并思考问题。展示教学目标。 .
复习旧知 锐角三角函数;仰家俯角概念; 教师提问,学生回答。
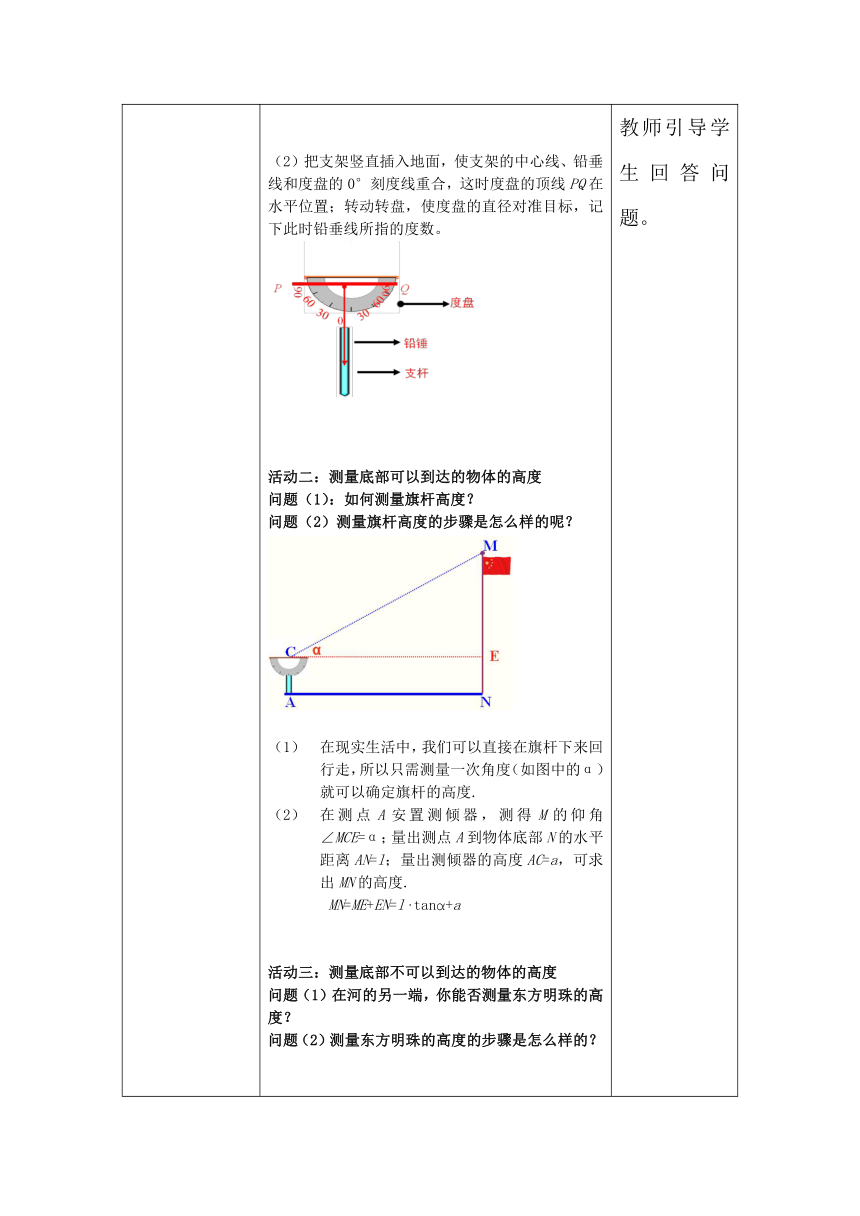
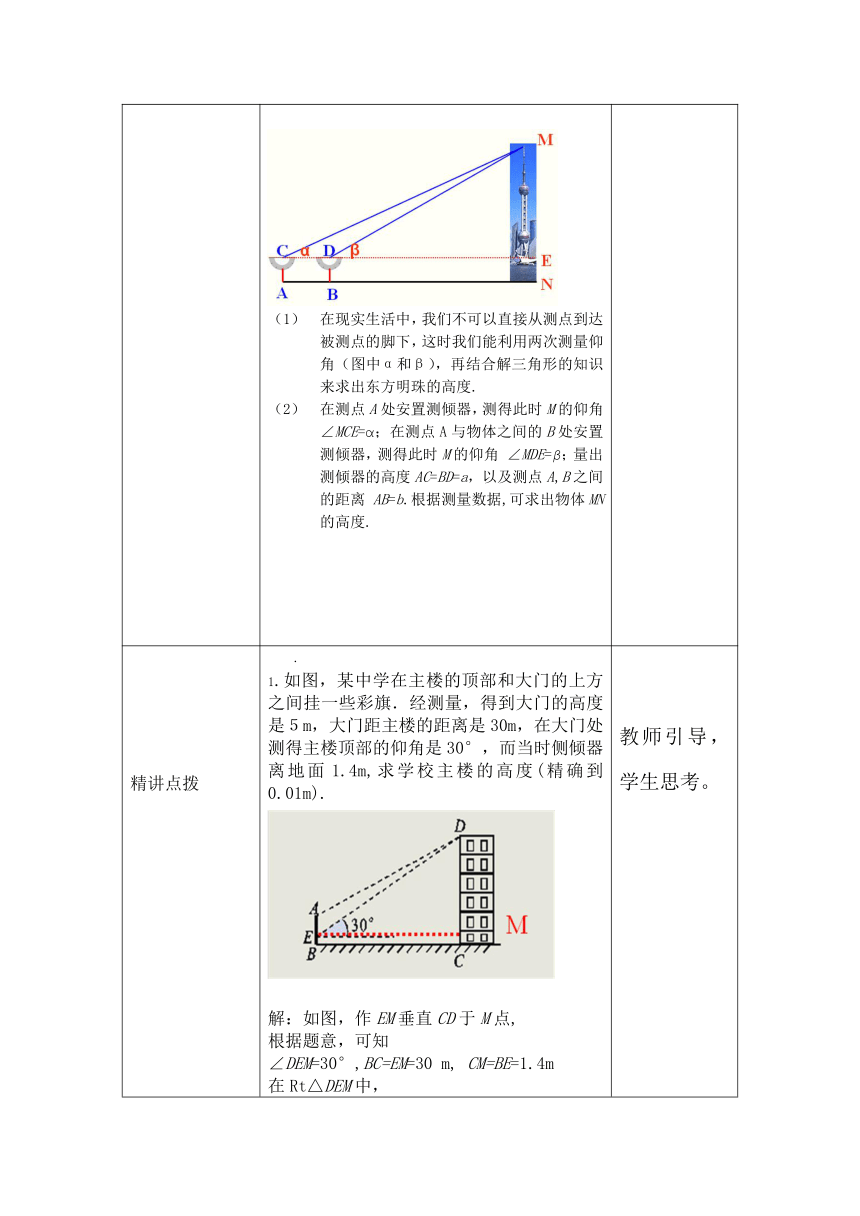
讲授新课(展示交流) 活动一:测量倾斜角问题1:如何测量倾斜角?问题2:如何使用侧倾器? (1)测量倾斜角可以用测倾器, ----简单的侧倾器由度盘、铅锤和支杆组成。(2)把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置;转动转盘,使度盘的直径对准目标,记下此时铅垂线所指的度数。活动二:测量底部可以到达的物体的高度问题(1):如何测量旗杆高度?问题(2)测量旗杆高度的步骤是怎么样的呢? 在现实生活中,我们可以直接在旗杆下来回行走,所以只需测量一次角度(如图中的α)就可以确定旗杆的高度.在测点A安置测倾器,测得M的仰角∠MCE=α;量出测点A到物体底部N的水平距离AN=l;量出测倾器的高度AC=a,可求出MN的高度.MN=ME+EN=l·tanα+a活动三:测量底部不可以到达的物体的高度问题(1)在河的另一端,你能否测量东方明珠的高度?问题(2)测量东方明珠的高度的步骤是怎么样的?在现实生活中,我们不可以直接从测点到达被测点的脚下,这时我们能利用两次测量仰角(图中α和β),再结合解三角形的知识来求出东方明珠的高度.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;在测点A与物体之间的B处安置测倾器,测得此时M的仰角 ∠MDE=β;量出测倾器的高度AC=BD=a,以及测点A,B之间的距离 AB=b.根据测量数据,可求出物体MN的高度. 教师引导学生回答问题。
精讲点拨 .1.如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度(精确到0.01m).解:如图,作EM垂直CD于M点,根据题意,可知∠DEM=30°,BC=EM=30 m, CM=BE=1.4m在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m),CD=DM+CM=17.32+1.4=18.72(m). 2. 下表是小亮所填实习报告的部分内容,请根据数据求大楼的高. 教师引导,学生思考。
当堂检测 1. 如图,在一次数学课外实践活动中,要求测教学楼AB的高度.小刚在D处用高1.5 m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40 m到达EF,又测得教学楼顶端A的仰角为60°.这幢教学楼AB的高度是 ( )。 2.如图某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C 到旗杆的距离(即CE的长)为8米,测得旗杆顶的仰角∠ECA为30°,旗杆底部的俯角∠ECB为45 °,则旗杆AB的高度是( )米。 学生独立完成后教师点拨
课堂小结 本节课你有什么收获?你能列出知识框架图吗?
分层作业 A组: P26 17 ,21 题; B组: P26 16,17题。
板书设计
教学反思
北师大 科目 数学 年级 九年级 下 册
课题 1.6 利用三角函数测高
教学目标 会利用直角三角形的边角关系测物体的高度。
教学重点 会利用直角三角形的边角关系测物体的高度。
教学难点 理解直角三角形的边角关系的意义和与现实生活的联系.
教学方法 本节课教师采取了启发、引导、提问、点拨等教学方式,让学生在实践探究和思考中学习。
学法指导 学生通过自主学习、动手实践、交流讨论、学习展示等学法进行学习,同时对于同伴们的分享和老师的点拨及时倾听,内化为自己的东西。数学学习过程应该是大胆猜想—实践探究—案例验证—总结提升的过程
教具准备 数学课本 绩优学案 教师用书
教学过程 问题设置 师生活动
情景引入 展示图片,并思考问题。展示教学目标。 .
复习旧知 锐角三角函数;仰家俯角概念; 教师提问,学生回答。
讲授新课(展示交流) 活动一:测量倾斜角问题1:如何测量倾斜角?问题2:如何使用侧倾器? (1)测量倾斜角可以用测倾器, ----简单的侧倾器由度盘、铅锤和支杆组成。(2)把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置;转动转盘,使度盘的直径对准目标,记下此时铅垂线所指的度数。活动二:测量底部可以到达的物体的高度问题(1):如何测量旗杆高度?问题(2)测量旗杆高度的步骤是怎么样的呢? 在现实生活中,我们可以直接在旗杆下来回行走,所以只需测量一次角度(如图中的α)就可以确定旗杆的高度.在测点A安置测倾器,测得M的仰角∠MCE=α;量出测点A到物体底部N的水平距离AN=l;量出测倾器的高度AC=a,可求出MN的高度.MN=ME+EN=l·tanα+a活动三:测量底部不可以到达的物体的高度问题(1)在河的另一端,你能否测量东方明珠的高度?问题(2)测量东方明珠的高度的步骤是怎么样的?在现实生活中,我们不可以直接从测点到达被测点的脚下,这时我们能利用两次测量仰角(图中α和β),再结合解三角形的知识来求出东方明珠的高度.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;在测点A与物体之间的B处安置测倾器,测得此时M的仰角 ∠MDE=β;量出测倾器的高度AC=BD=a,以及测点A,B之间的距离 AB=b.根据测量数据,可求出物体MN的高度. 教师引导学生回答问题。
精讲点拨 .1.如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度(精确到0.01m).解:如图,作EM垂直CD于M点,根据题意,可知∠DEM=30°,BC=EM=30 m, CM=BE=1.4m在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m),CD=DM+CM=17.32+1.4=18.72(m). 2. 下表是小亮所填实习报告的部分内容,请根据数据求大楼的高. 教师引导,学生思考。
当堂检测 1. 如图,在一次数学课外实践活动中,要求测教学楼AB的高度.小刚在D处用高1.5 m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40 m到达EF,又测得教学楼顶端A的仰角为60°.这幢教学楼AB的高度是 ( )。 2.如图某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C 到旗杆的距离(即CE的长)为8米,测得旗杆顶的仰角∠ECA为30°,旗杆底部的俯角∠ECB为45 °,则旗杆AB的高度是( )米。 学生独立完成后教师点拨
课堂小结 本节课你有什么收获?你能列出知识框架图吗?
分层作业 A组: P26 17 ,21 题; B组: P26 16,17题。
板书设计
教学反思
