全等三角形的判定 SAS(陕西省渭南市大荔县)
文档属性
| 名称 | 全等三角形的判定 SAS(陕西省渭南市大荔县) |

|
|
| 格式 | rar | ||
| 文件大小 | 170.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-03 00:00:00 | ||
图片预览


文档简介
课件17张PPT。全等三角形的判定
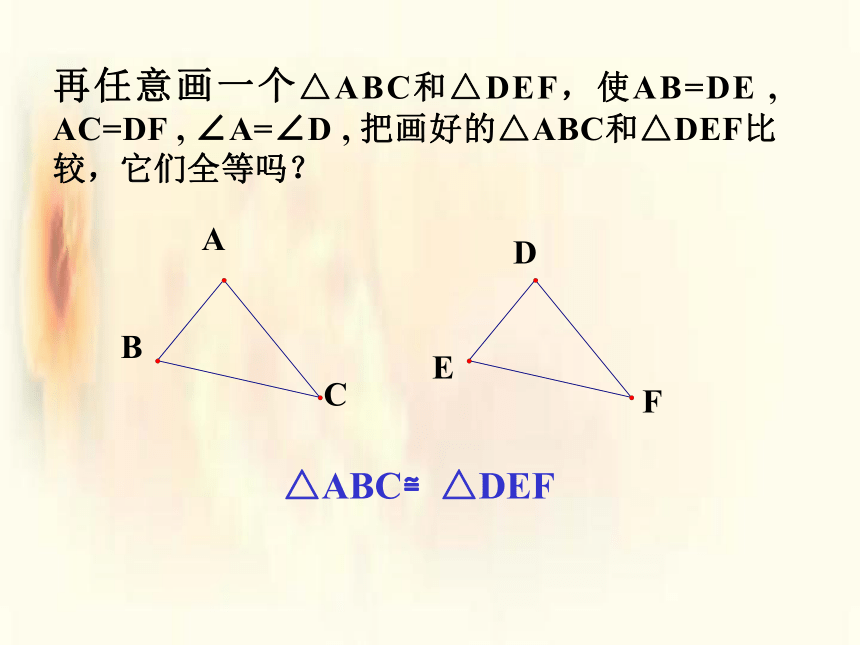
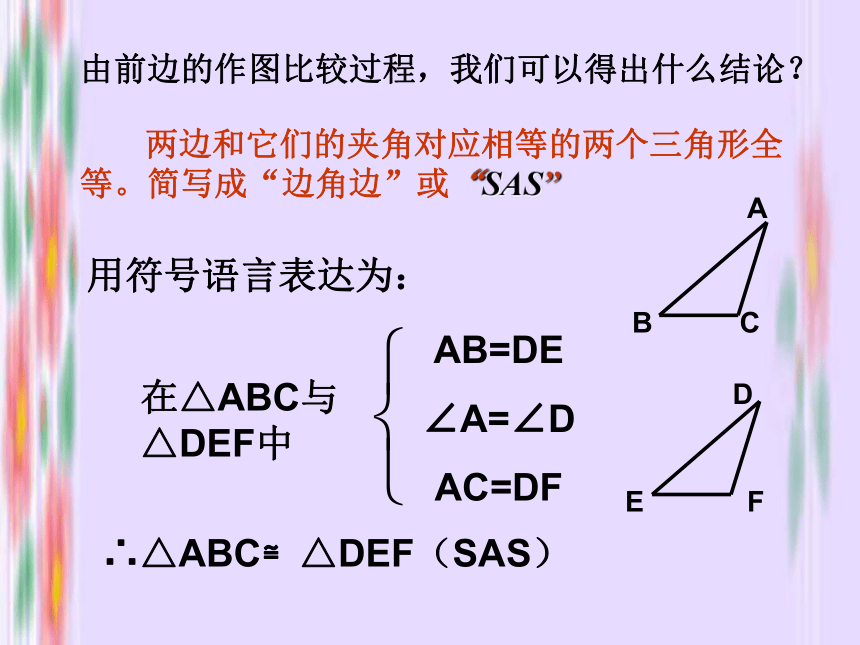
(SAS)画△ABC,使AB=3cm,AC=4cm。画法:2. 在射线AM上截取AB= 3cm3. 在射线AN上截取AC=4cm 这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?若再加一个条件,使∠A=45°,画出△ABC1. 画∠MAN= 45°4.连接BC则△ABC就是所求的三角形把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?画一画再任意画一个△ABC和△DEF,使AB=DE , AC=DF , ∠A=∠D , 把画好的△ABC和△DEF比较,它们全等吗?DEF△ABC≌△DEF由前边的作图比较过程,我们可以得出什么结论?用符号语言表达为:在△ABC与△DEF中AB=DE
∠A=∠D
AC=DF∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
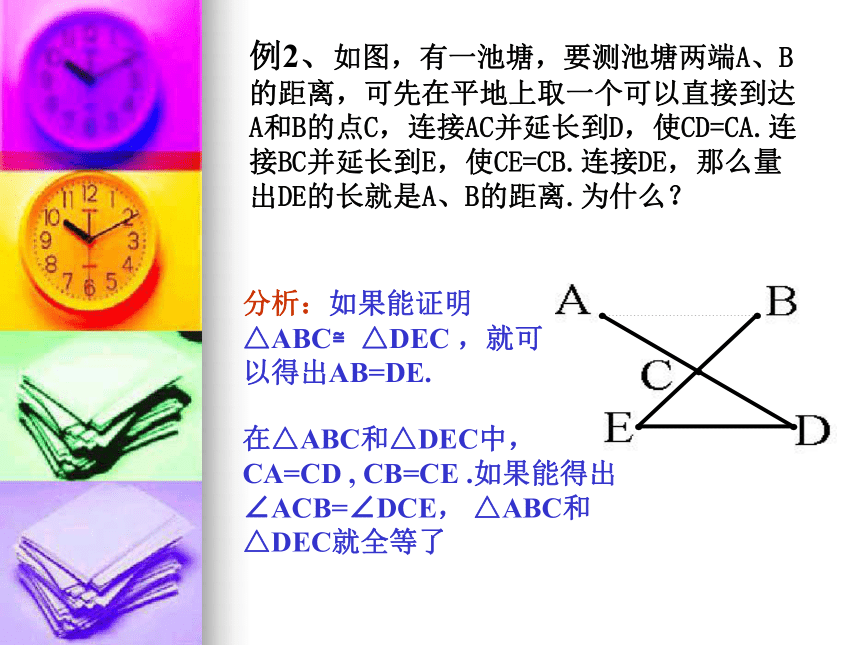
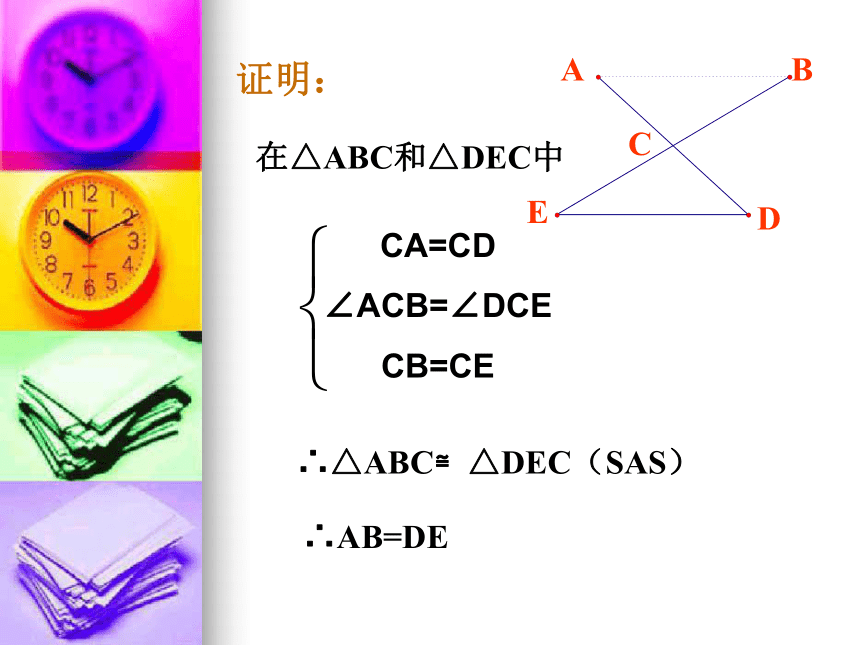
例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?分析:如果能证明△ABC≌△DEC ,就可以得出AB=DE.在△ABC和△DEC中,CA=CD , CB=CE .如果能得出∠ACB=∠DCE, △ABC和△DEC就全等了ABCDE证明:在△ABC和△DEC中CA=CD
∠ACB=∠DCE
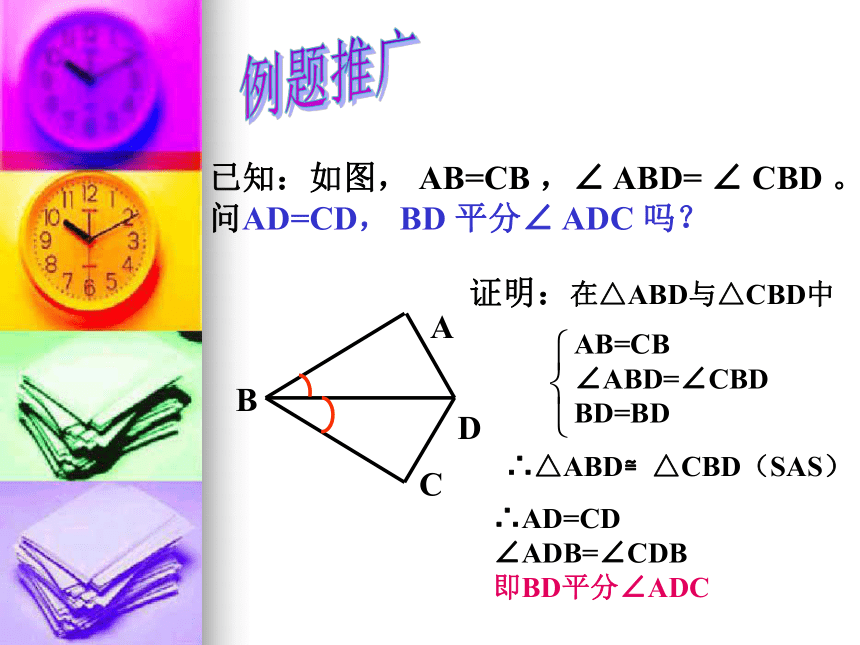
CB=CE∴△ABC≌△DEC(SAS)∴AB=DE已知:如图, AB=CB ,∠ ABD= ∠ CBD 。
问AD=CD, BD 平分∠ ADC 吗?例题推广证明:在△ABD与△CBD中AB=CB
∠ABD=∠CBD
BD=BD∴△ABD≌△CBD(SAS)∴AD=CD
∠ADB=∠CDB
即BD平分∠ADC
因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。由前边两个题目可以看出:探究两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?动画演示这说明:有两边和其中一边的对角对应相等的两个三角形不一定全等。例: 已知有4个三角形,它们有如下的关系:
A1B1=A2B2=A3B3=AB,
∠B1=∠B2=∠B3=∠B,
B1C1<B2C2=BC<B3C3 .
问△ABC与其余三个三角形中的哪一个全等.【解】我们把甲、乙、丙三个三角形移动后覆盖在△ABC上,使得A1B1,A2B2,A3B3和AB重合,∠B1、∠B2、∠B3和∠B重合,C1和C2、C3将落在直线BC上,其中:
(1)由于B1C1<BC,所以点C1在C的左侧,可知△A1B1C1和△ABC不全等; (2)由于B3C3>BC,所以点C3在点C的右侧,可知△A3B3C3和△ABC也不全等;
(3)由于B2C2=BC,所以点C2和点C重合,于是B2C2与BC重合,A2C2和CA也重合,则可知△A2B2C2与△ABC重合,即
△A2B2C2≌△ABC .练一练1、如图,B点在A点的正北方向。两车从路段AB的一端A出发,分别向东、向西进行相同的距离,到达C、D两地。此时C,D到B的距离相等吗?为什么?BDAC【证明】∵在△BAD和△BAC中,BA=BA
∠BAD=∠BAC
AD=AC则△BAD≌△BAC (SAS).即BD=BC2、如图,点E、F在BC上,BE=CF,AB=DC, ∠B=∠C,求证: ∠A=∠DADBEFC【证明】∵BF=BE+EF
CE=CF+FE
而BE=CF
∴BF=CE在△ABF和△DCE中,
BF=CE
∠B=∠C
AB=DC则△BAD≌△BAC (SAS).即∠A=∠D
例题拓广已知:如图,AD∥BC,AD=CB. 求证:AB=CD.【提示】连结AC,
由 △ABC≌△CDA
故 AB=CD.
课堂小结:2. 用尺规作图:已知两边及其夹角的三角形1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)课本104页3、4题
同步练习布置作业:
(SAS)画△ABC,使AB=3cm,AC=4cm。画法:2. 在射线AM上截取AB= 3cm3. 在射线AN上截取AC=4cm 这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?若再加一个条件,使∠A=45°,画出△ABC1. 画∠MAN= 45°4.连接BC则△ABC就是所求的三角形把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?画一画再任意画一个△ABC和△DEF,使AB=DE , AC=DF , ∠A=∠D , 把画好的△ABC和△DEF比较,它们全等吗?DEF△ABC≌△DEF由前边的作图比较过程,我们可以得出什么结论?用符号语言表达为:在△ABC与△DEF中AB=DE
∠A=∠D
AC=DF∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
例2、如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?分析:如果能证明△ABC≌△DEC ,就可以得出AB=DE.在△ABC和△DEC中,CA=CD , CB=CE .如果能得出∠ACB=∠DCE, △ABC和△DEC就全等了ABCDE证明:在△ABC和△DEC中CA=CD
∠ACB=∠DCE
CB=CE∴△ABC≌△DEC(SAS)∴AB=DE已知:如图, AB=CB ,∠ ABD= ∠ CBD 。
问AD=CD, BD 平分∠ ADC 吗?例题推广证明:在△ABD与△CBD中AB=CB
∠ABD=∠CBD
BD=BD∴△ABD≌△CBD(SAS)∴AD=CD
∠ADB=∠CDB
即BD平分∠ADC
因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。由前边两个题目可以看出:探究两边和它们的夹角对应相等的两个三角形全等。由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?动画演示这说明:有两边和其中一边的对角对应相等的两个三角形不一定全等。例: 已知有4个三角形,它们有如下的关系:
A1B1=A2B2=A3B3=AB,
∠B1=∠B2=∠B3=∠B,
B1C1<B2C2=BC<B3C3 .
问△ABC与其余三个三角形中的哪一个全等.【解】我们把甲、乙、丙三个三角形移动后覆盖在△ABC上,使得A1B1,A2B2,A3B3和AB重合,∠B1、∠B2、∠B3和∠B重合,C1和C2、C3将落在直线BC上,其中:
(1)由于B1C1<BC,所以点C1在C的左侧,可知△A1B1C1和△ABC不全等; (2)由于B3C3>BC,所以点C3在点C的右侧,可知△A3B3C3和△ABC也不全等;
(3)由于B2C2=BC,所以点C2和点C重合,于是B2C2与BC重合,A2C2和CA也重合,则可知△A2B2C2与△ABC重合,即
△A2B2C2≌△ABC .练一练1、如图,B点在A点的正北方向。两车从路段AB的一端A出发,分别向东、向西进行相同的距离,到达C、D两地。此时C,D到B的距离相等吗?为什么?BDAC【证明】∵在△BAD和△BAC中,BA=BA
∠BAD=∠BAC
AD=AC则△BAD≌△BAC (SAS).即BD=BC2、如图,点E、F在BC上,BE=CF,AB=DC, ∠B=∠C,求证: ∠A=∠DADBEFC【证明】∵BF=BE+EF
CE=CF+FE
而BE=CF
∴BF=CE在△ABF和△DCE中,
BF=CE
∠B=∠C
AB=DC则△BAD≌△BAC (SAS).即∠A=∠D
例题拓广已知:如图,AD∥BC,AD=CB. 求证:AB=CD.【提示】连结AC,
由 △ABC≌△CDA
故 AB=CD.
课堂小结:2. 用尺规作图:已知两边及其夹角的三角形1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)课本104页3、4题
同步练习布置作业:
