5.1探索三角形相似的条件(1) (山东省烟台市海阳市)
文档属性
| 名称 | 5.1探索三角形相似的条件(1) (山东省烟台市海阳市) |  | |
| 格式 | rar | ||
| 文件大小 | 797.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-02 19:53:00 | ||
图片预览







文档简介
课件21张PPT。5 探索三角形相似的条件(1) 小纪一中 八三班
刘英梅1.知识目标:
经历“直观感觉――动手感知――理性思维”的活动过程,探索两个三角形相似的条件,并会用相似三角形的判定方法一进行判断及计算。2.能力目标:
通过三角形相似的条件的探索及应用,进一步发展合情推理能力和初步的逻辑推理能力。学习目标3、情感目标:
能极积参与数学学习活动,体验数学活动充满着探索与创造。培养学生的发散性思维,以及动手、动脑和谐一致的习惯。判定两个三角形全等方法,
SSS , SAS , ASA , AAS 。 在直角三角形中还有一种方法为 。HL1、什么是相似三角形?
三个角对应相等,三条边对应成比例的两个三角形叫做相似三角形。
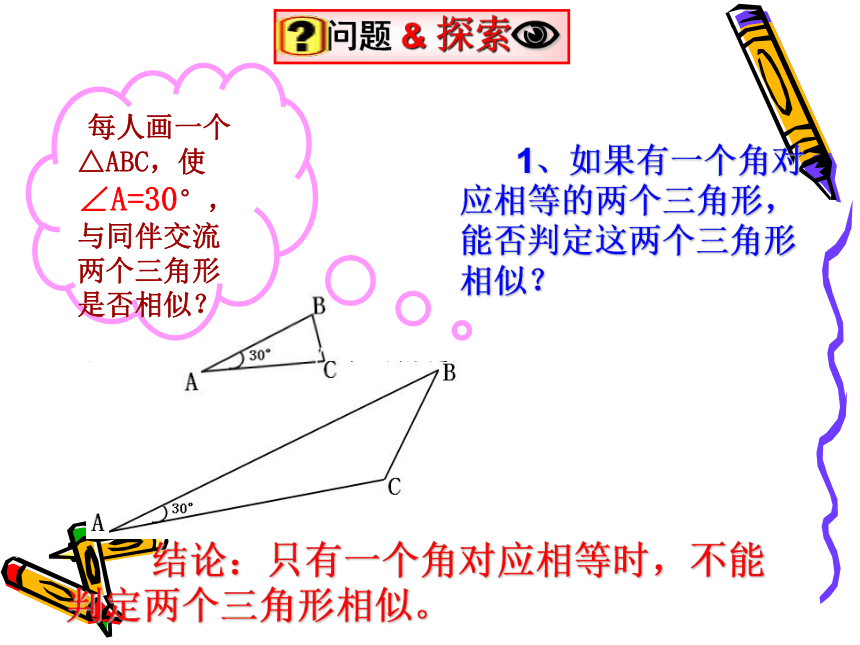
2、判定两个三角形全等有哪些方法? 1、如果有一个角对应相等的两个三角形,能否判定这两个三角形相似? 结论:只有一个角对应相等时,不能判定两个三角形相似。 每人画一个△ABC,使∠A=30°,与同伴交流两个三角形是否相似?
与同伴合作画三角形一人画⊿ABC,另一人画△ABC,使∠A和∠A′都等于30°, ∠B和∠B′都等于45° ⊙比较你们画的两个三角形, ∠C与∠C′相等吗?⊙这样的两个三角形相似吗?若∠A 和∠A′都等于40°,∠B和∠B′都等于60°,你们画的两个三角形相似吗?
2、如果有两个角对应相等的两个三角形,能否判定这两个三角形相似?
通过以上动手作图,我们有什么结论?得出两角对应相等的两个三角形相似。
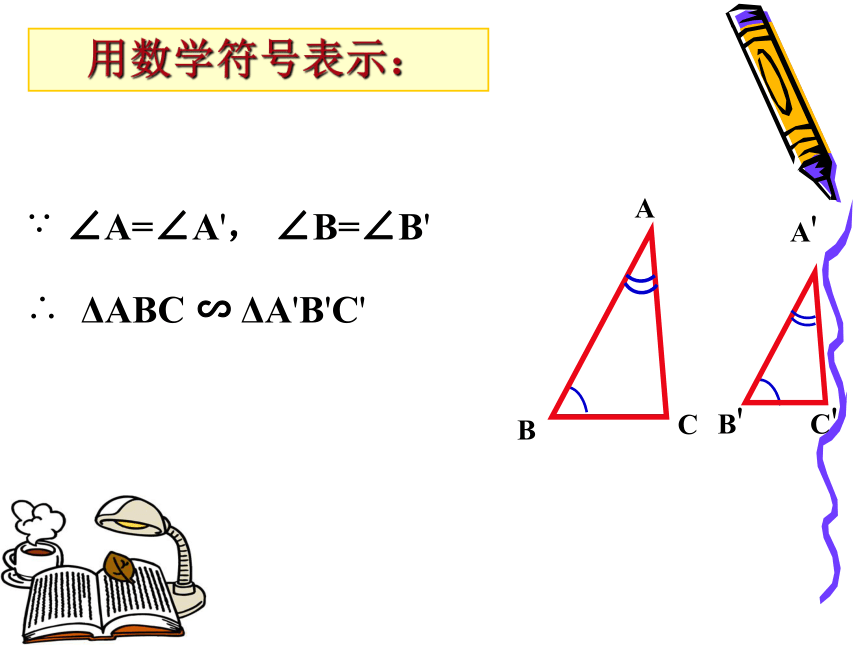
这是一个今后经常用来判定两个三角形相似的重要方法CC'∠A=∠A', ∠B=∠B'ΔABC ∽ ΔA'B'C'用数学符号表示:
1、议一议:(1)有一个锐角相等的两个直角三角形是否相似?为什么?
(2)一个角相等的两个等腰三角形相似吗?为什么?应用规律,巩固新知第一种情况∴ ΔABC ∽ ΔA'B'C'第二种情况∴ ΔABC ∽ ΔA'B'C'第三种情况两三角形不相似行家看“门道”例 如图4-17,D,E分别是△ ABC边AB,AC上的点,DE∥BC.图中有哪些相等的角?
找出图中的相似三角形,并说明理由;
写出三组成比例的线段.解:(1) DE∥BC∠ADE=∠B,
∠AED=∠C.(2) △ ADE∽ △ABC.理由是:∠ADE=∠B
∠AED=∠C △ ADE∽ △ABC.
(两角对应相等的两个三角形相似)(3) △ ADE∽ △ABC(相似三角形对应边成比例.)(两直线平行,同位角相等.)发散探究例 如图4-17,D,E分别是△ ABC边AB,AC上的点,DE∥BC.解:由上面(3)题可知:
△ ADE∽ △ABC即在以后求证线段成比例时,
可考虑用两个三角形相似。1、如图,为了测量一条河流的宽度,勘测人员观察到河对岸一个特别明显的标志点O,再在他们所在的河岸选择点A、B、D,使得AB┴AO,DB┴AB,然后确定DO和AB的交点C,测得AC=120米,CB=60米,BD=50米.你能帮助他们算出河流AO的宽吗?联系拓展自我评价,检测反馈: (一)学习体会:本节你有哪些收获?还有哪些疑惑?
(二)当堂检测:
1、判断题(正确的打√,错误的打×)
(1)任意两个直角三角形相似 ( )
(2)任意两个等腰三角形相似 ( )
(3)任意两个等腰直角三角形相似 ( )
(4)任意两个等边三角形相似 ( )
(5)全等三角形是相似三角形 ( )
(6)相似三角形一定是全等三角形 ( )××√√√×2、如图,梯形ABCD的两条对角线相交与点O,找出图中的相似三角形,并说明理由.课外自评 2、如图,已知△ABC,用尺规做一个三角形,使作出的三角形与△ABC相似,并且相似比为2:1
1、如图,点D是△ABC边AC上的点且∠ABD=∠C,△ABC与△ABD相似吗? ADCB解后反思:运用条件一判定两个三角形相似时,如何找准两对相等的角? 突破找角的难点:
1.注意图形中的公共角、对顶角、直角
2.两直线平行时的同位角、内错角
3.或等角的余角、补角等等.
谢谢指导再见
刘英梅1.知识目标:
经历“直观感觉――动手感知――理性思维”的活动过程,探索两个三角形相似的条件,并会用相似三角形的判定方法一进行判断及计算。2.能力目标:
通过三角形相似的条件的探索及应用,进一步发展合情推理能力和初步的逻辑推理能力。学习目标3、情感目标:
能极积参与数学学习活动,体验数学活动充满着探索与创造。培养学生的发散性思维,以及动手、动脑和谐一致的习惯。判定两个三角形全等方法,
SSS , SAS , ASA , AAS 。 在直角三角形中还有一种方法为 。HL1、什么是相似三角形?
三个角对应相等,三条边对应成比例的两个三角形叫做相似三角形。
2、判定两个三角形全等有哪些方法? 1、如果有一个角对应相等的两个三角形,能否判定这两个三角形相似? 结论:只有一个角对应相等时,不能判定两个三角形相似。 每人画一个△ABC,使∠A=30°,与同伴交流两个三角形是否相似?
与同伴合作画三角形一人画⊿ABC,另一人画△ABC,使∠A和∠A′都等于30°, ∠B和∠B′都等于45° ⊙比较你们画的两个三角形, ∠C与∠C′相等吗?⊙这样的两个三角形相似吗?若∠A 和∠A′都等于40°,∠B和∠B′都等于60°,你们画的两个三角形相似吗?
2、如果有两个角对应相等的两个三角形,能否判定这两个三角形相似?
通过以上动手作图,我们有什么结论?得出两角对应相等的两个三角形相似。
这是一个今后经常用来判定两个三角形相似的重要方法CC'∠A=∠A', ∠B=∠B'ΔABC ∽ ΔA'B'C'用数学符号表示:
1、议一议:(1)有一个锐角相等的两个直角三角形是否相似?为什么?
(2)一个角相等的两个等腰三角形相似吗?为什么?应用规律,巩固新知第一种情况∴ ΔABC ∽ ΔA'B'C'第二种情况∴ ΔABC ∽ ΔA'B'C'第三种情况两三角形不相似行家看“门道”例 如图4-17,D,E分别是△ ABC边AB,AC上的点,DE∥BC.图中有哪些相等的角?
找出图中的相似三角形,并说明理由;
写出三组成比例的线段.解:(1) DE∥BC∠ADE=∠B,
∠AED=∠C.(2) △ ADE∽ △ABC.理由是:∠ADE=∠B
∠AED=∠C △ ADE∽ △ABC.
(两角对应相等的两个三角形相似)(3) △ ADE∽ △ABC(相似三角形对应边成比例.)(两直线平行,同位角相等.)发散探究例 如图4-17,D,E分别是△ ABC边AB,AC上的点,DE∥BC.解:由上面(3)题可知:
△ ADE∽ △ABC即在以后求证线段成比例时,
可考虑用两个三角形相似。1、如图,为了测量一条河流的宽度,勘测人员观察到河对岸一个特别明显的标志点O,再在他们所在的河岸选择点A、B、D,使得AB┴AO,DB┴AB,然后确定DO和AB的交点C,测得AC=120米,CB=60米,BD=50米.你能帮助他们算出河流AO的宽吗?联系拓展自我评价,检测反馈: (一)学习体会:本节你有哪些收获?还有哪些疑惑?
(二)当堂检测:
1、判断题(正确的打√,错误的打×)
(1)任意两个直角三角形相似 ( )
(2)任意两个等腰三角形相似 ( )
(3)任意两个等腰直角三角形相似 ( )
(4)任意两个等边三角形相似 ( )
(5)全等三角形是相似三角形 ( )
(6)相似三角形一定是全等三角形 ( )××√√√×2、如图,梯形ABCD的两条对角线相交与点O,找出图中的相似三角形,并说明理由.课外自评 2、如图,已知△ABC,用尺规做一个三角形,使作出的三角形与△ABC相似,并且相似比为2:1
1、如图,点D是△ABC边AC上的点且∠ABD=∠C,△ABC与△ABD相似吗? ADCB解后反思:运用条件一判定两个三角形相似时,如何找准两对相等的角? 突破找角的难点:
1.注意图形中的公共角、对顶角、直角
2.两直线平行时的同位角、内错角
3.或等角的余角、补角等等.
谢谢指导再见
