5.3等效电路 课件(共26张PPT)2023-2024学年教科版九年级上册物理
文档属性
| 名称 | 5.3等效电路 课件(共26张PPT)2023-2024学年教科版九年级上册物理 |

|
|
| 格式 | pptx | ||
| 文件大小 | 995.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-02 18:35:36 | ||
图片预览








文档简介
(共26张PPT)
第五章 欧姆定律
3.等效电路
1.进一步了解串、并联电路特点,了解等效电阻、电路。
2.能推导并认识串、并联电路中电阻的特点。
3.学习不同的探究方法,能运用等效法看问题并将问题简化。
◎重点:推导并认识串并联电路中电阻的特点。
通过任务驱动一、二完成目标2的学习。
电路的等效电阻
1.几个连接起来的电阻所起的作用,可以用一个电阻来代替,这个电阻就是那些电阻的 等效 电阻。
等效
2.实验中将两个定值电阻R1、R2串联起来,用电压表测量他们的总电压,用电流表测出通过它们的电流,由公式 R= 可求出两电阻串联后的等效电阻。
R=
串联电路的等效电阻
3.思考:该实验中,如何使实验结论更具有普遍性,更具有说服力呢?
在电路中串联一个 滑动变阻器 ,改变电阻R1、R2两端的总电压以及通过它们的电流,多次验证 等效电阻R 和 R1、R2 的关系,就可以使实验结论更具有说服力。
滑动变阻器
等效电阻R
R1、R2
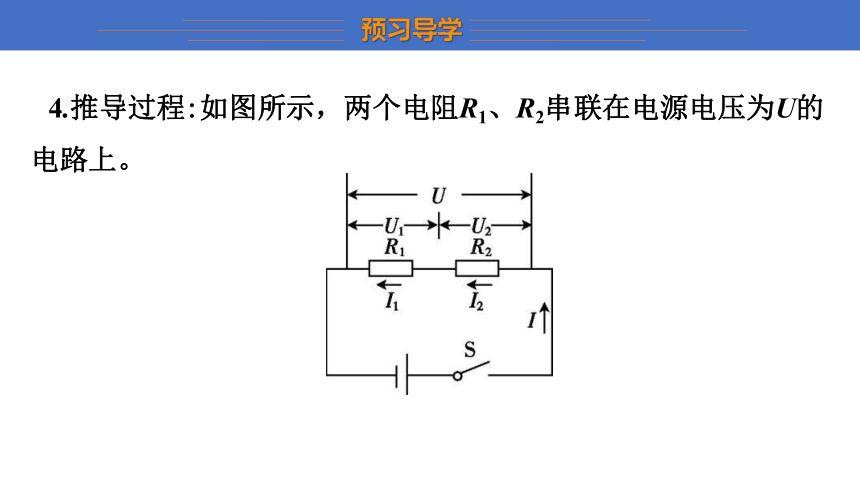
4.推导过程:如图所示,两个电阻R1、R2串联在电源电压为U的电路上。
根据“串联电路中,电流 处处相等 ”的特点可知, I=I1=I2 。
根据“串联电路中总电压等于各部分电路电压 之和 ”的特点可知U= U1+U2 (①式)。
根据欧姆定律可知电阻R1、R2两端的总电压 U=IR(②式),分电阻R1两端的电压U1= I1R1 (③式),R2两端的电压U2= I2R2 (④式)。
处处相等
I=I1
=I2
之和
U1+U2
I1R1
I2R2
将②、③、④式代入①式得到关系式IR= I1R1+I2R2 ,化简得R= R1+R2 ,即串联电路的等效电阻等于各串联电阻 之和 。
5.由图可知,串联电路的等效电阻的 长度 比任何一个分电阻的 长度 都大,因此,等效电阻的阻值也一定比任何一个分电阻的阻值都大。
I1R1+I2R2
R1+R2
之和
长度
长度
几个电阻(导体)串联起来,相当于增加了电阻(导体)的长度,等效电阻变大,等效电阻比串联的任何一个电阻的阻值都要大。
1.电器修理工小李需要一只60 Ω的电阻,他可以选择一只 20 Ω的电阻和一只40 Ω的电阻串联得到。
并联电路的等效电阻
7.两个电阻并联后,等效电阻的 横截面积 比任何一个分电阻的 横截面积 都大,因此可以猜想等效电阻的阻值比任何一个分电阻的阻值都 小 。
20
横截面积
横截面积
小
8.推导过程:将两个电阻R1、R2并联在电源电压为U的电路上,试联系并联电路电压、电流的规律和欧姆定律,推导出并联电路的等效电阻的表达式。
根据并联电路的电压特点可知, U=U1=U2 ;
根据并联电路的电流特点可知, I=I1+I2 ;
根据欧姆定律可知,I=,I1= ,I2= ;
联立可得,=+,即= + 。
U=U1=U2
I=I1+I2
+
2.在并联电路中,关于电流、电压、电阻的叙述,不正确的是 ( B )
A.总电流等于各支路中电流之和
B.总电阻等于各支路中电阻的倒数之和
C.各支路两端电压相等
D.总电阻比各支路电阻小
B
几个电阻(导体)并联起来,相当于增加了电阻(导体)的横截面积,等效电阻变小,等效电阻比并联的任何一个电阻的阻值都要小。
等效电路
9.在分析一些复杂电路时,人们常常只关注整个电路(或电路的某一部分)的输入、输出关系,即 电流 和 电压 的变化关系。用一个简单的电路代替复杂电路,使问题得到简化,这个简单的电路就是复杂电路的 等效电路 。
电流
电压
等效电路
3.如图所示的电路,电源电压恒定不变,当S1闭合、S2断开时,电压表的示数为3 V,当S1断开、S2闭合时,电压表的示数为9 V,则R1∶R2为 ( C )
A.1∶3
B.3∶1
C.1∶2
D.2∶1
C
电阻的串联
提出问题:电阻串联后,其总电阻是增大还是减小?
作出假设:由于导体的电阻与导体的长度有关,导体越长,电阻 越大 ,几个电阻串联后相当于增加了 导体的长度 。因此猜想,电阻串联后,总电阻会 增大 。
越大
导体的长度
增大
设计实验并进行实验:在如图甲所示的电路图A、B处,分别接入如图乙中的一个电阻R、两个串联的电阻R、三个串联的电阻R,分别读出 电流表的示数 。
电流表的示数
甲
乙
分析与论证:通过观察对比 电流表的示数 ,发现电流表的示数一次比一次 小 ,电路两端的电压 不变 ,可知电路中电阻 增大 。
实验结论:串联电阻的 总电阻 的阻值比任何一个 分电阻 的阻值都大。
电流表的示数
小
不变
增大
总电阻
分电阻
理论推导:如图所示,设电路电流I,电源电压为U,R1两端的电压为U1,R2两端的电压为U2,电路总电阻为R,由欧姆定律可得,U=IR,U1=I1R1,U2=I2R2。因为串联电路中U= U1+U2 ,所以IR= I1R1+I2R2 ,又因为串联电路中I=I1=I2,所以R= R1+R2 。
U1+
U2
I1R1+I2R2
R1+R2
串联电阻的实质:几个电阻串联,相当于 增加了导体的长度 ,因而总电阻比其中任何一个电阻都要 大 ,有n个相同的电阻串联,其总电阻R= nR0 。
增加了导体的长
度
大
nR0
若有n个电阻串联,则有R=R1+R2+ R3…+Rn,即串联电路的总电阻等于 各串联电阻之和 。
各串联电阻之和
电阻的并联
提出问题:电阻并联后总电阻变大了还是变小了?
作出假设:由于导体的电阻与导体的 横截面积 有关,横截面积越大,电阻 越小 ,几个电阻并联后相当于增加了导体 横截面积 。因此猜想:电阻并联后,总电阻会 变小 。
横截面积
越小
横截面积
变小
设计并进行实验:在如图所示电路图A、B处,分别接入图中的一个电阻R、两个并联的电阻R、三个并联的电阻R,分别读出 电流表示数 。
电流表示数
分析与论证:通过对比观察电流表示数,可以发现电流表示数一次比一次大,电路两端的电压 不变 ,可知电路中电阻 减小 。
不变
减小
实验结论:并联电路的总电阻的 阻值 比任何一个 分电阻阻值都小 。
理论推导:如图所示,设支路电阻分别为R1和R2,电路两端的电压为U。并联时,总电流等于 各支路电流之和 ,则有I=I1+I2,因为I=,I1=,I2=,所以=+,又因为在并联电路中,U=U1=U2,所以=+。
阻值
分电阻
阻值都小
各支路电流之和
若有n个电阻并联,则有=++…+,即并联电路的总电阻的 倒数 ,等于各并联电阻的 倒数之和 。
倒数
倒数之和
并联电阻的实质:几个电阻并联,相当于增大了电阻的 横截面积 ,因而总电阻 会变小(比最小的电阻还要小) ,有n个阻值为R0的 相同 电阻并联,其总电阻R= 。
横截
面积
会变小(比最小的电阻还要小)
相同
第五章 欧姆定律
3.等效电路
1.进一步了解串、并联电路特点,了解等效电阻、电路。
2.能推导并认识串、并联电路中电阻的特点。
3.学习不同的探究方法,能运用等效法看问题并将问题简化。
◎重点:推导并认识串并联电路中电阻的特点。
通过任务驱动一、二完成目标2的学习。
电路的等效电阻
1.几个连接起来的电阻所起的作用,可以用一个电阻来代替,这个电阻就是那些电阻的 等效 电阻。
等效
2.实验中将两个定值电阻R1、R2串联起来,用电压表测量他们的总电压,用电流表测出通过它们的电流,由公式 R= 可求出两电阻串联后的等效电阻。
R=
串联电路的等效电阻
3.思考:该实验中,如何使实验结论更具有普遍性,更具有说服力呢?
在电路中串联一个 滑动变阻器 ,改变电阻R1、R2两端的总电压以及通过它们的电流,多次验证 等效电阻R 和 R1、R2 的关系,就可以使实验结论更具有说服力。
滑动变阻器
等效电阻R
R1、R2
4.推导过程:如图所示,两个电阻R1、R2串联在电源电压为U的电路上。
根据“串联电路中,电流 处处相等 ”的特点可知, I=I1=I2 。
根据“串联电路中总电压等于各部分电路电压 之和 ”的特点可知U= U1+U2 (①式)。
根据欧姆定律可知电阻R1、R2两端的总电压 U=IR(②式),分电阻R1两端的电压U1= I1R1 (③式),R2两端的电压U2= I2R2 (④式)。
处处相等
I=I1
=I2
之和
U1+U2
I1R1
I2R2
将②、③、④式代入①式得到关系式IR= I1R1+I2R2 ,化简得R= R1+R2 ,即串联电路的等效电阻等于各串联电阻 之和 。
5.由图可知,串联电路的等效电阻的 长度 比任何一个分电阻的 长度 都大,因此,等效电阻的阻值也一定比任何一个分电阻的阻值都大。
I1R1+I2R2
R1+R2
之和
长度
长度
几个电阻(导体)串联起来,相当于增加了电阻(导体)的长度,等效电阻变大,等效电阻比串联的任何一个电阻的阻值都要大。
1.电器修理工小李需要一只60 Ω的电阻,他可以选择一只 20 Ω的电阻和一只40 Ω的电阻串联得到。
并联电路的等效电阻
7.两个电阻并联后,等效电阻的 横截面积 比任何一个分电阻的 横截面积 都大,因此可以猜想等效电阻的阻值比任何一个分电阻的阻值都 小 。
20
横截面积
横截面积
小
8.推导过程:将两个电阻R1、R2并联在电源电压为U的电路上,试联系并联电路电压、电流的规律和欧姆定律,推导出并联电路的等效电阻的表达式。
根据并联电路的电压特点可知, U=U1=U2 ;
根据并联电路的电流特点可知, I=I1+I2 ;
根据欧姆定律可知,I=,I1= ,I2= ;
联立可得,=+,即= + 。
U=U1=U2
I=I1+I2
+
2.在并联电路中,关于电流、电压、电阻的叙述,不正确的是 ( B )
A.总电流等于各支路中电流之和
B.总电阻等于各支路中电阻的倒数之和
C.各支路两端电压相等
D.总电阻比各支路电阻小
B
几个电阻(导体)并联起来,相当于增加了电阻(导体)的横截面积,等效电阻变小,等效电阻比并联的任何一个电阻的阻值都要小。
等效电路
9.在分析一些复杂电路时,人们常常只关注整个电路(或电路的某一部分)的输入、输出关系,即 电流 和 电压 的变化关系。用一个简单的电路代替复杂电路,使问题得到简化,这个简单的电路就是复杂电路的 等效电路 。
电流
电压
等效电路
3.如图所示的电路,电源电压恒定不变,当S1闭合、S2断开时,电压表的示数为3 V,当S1断开、S2闭合时,电压表的示数为9 V,则R1∶R2为 ( C )
A.1∶3
B.3∶1
C.1∶2
D.2∶1
C
电阻的串联
提出问题:电阻串联后,其总电阻是增大还是减小?
作出假设:由于导体的电阻与导体的长度有关,导体越长,电阻 越大 ,几个电阻串联后相当于增加了 导体的长度 。因此猜想,电阻串联后,总电阻会 增大 。
越大
导体的长度
增大
设计实验并进行实验:在如图甲所示的电路图A、B处,分别接入如图乙中的一个电阻R、两个串联的电阻R、三个串联的电阻R,分别读出 电流表的示数 。
电流表的示数
甲
乙
分析与论证:通过观察对比 电流表的示数 ,发现电流表的示数一次比一次 小 ,电路两端的电压 不变 ,可知电路中电阻 增大 。
实验结论:串联电阻的 总电阻 的阻值比任何一个 分电阻 的阻值都大。
电流表的示数
小
不变
增大
总电阻
分电阻
理论推导:如图所示,设电路电流I,电源电压为U,R1两端的电压为U1,R2两端的电压为U2,电路总电阻为R,由欧姆定律可得,U=IR,U1=I1R1,U2=I2R2。因为串联电路中U= U1+U2 ,所以IR= I1R1+I2R2 ,又因为串联电路中I=I1=I2,所以R= R1+R2 。
U1+
U2
I1R1+I2R2
R1+R2
串联电阻的实质:几个电阻串联,相当于 增加了导体的长度 ,因而总电阻比其中任何一个电阻都要 大 ,有n个相同的电阻串联,其总电阻R= nR0 。
增加了导体的长
度
大
nR0
若有n个电阻串联,则有R=R1+R2+ R3…+Rn,即串联电路的总电阻等于 各串联电阻之和 。
各串联电阻之和
电阻的并联
提出问题:电阻并联后总电阻变大了还是变小了?
作出假设:由于导体的电阻与导体的 横截面积 有关,横截面积越大,电阻 越小 ,几个电阻并联后相当于增加了导体 横截面积 。因此猜想:电阻并联后,总电阻会 变小 。
横截面积
越小
横截面积
变小
设计并进行实验:在如图所示电路图A、B处,分别接入图中的一个电阻R、两个并联的电阻R、三个并联的电阻R,分别读出 电流表示数 。
电流表示数
分析与论证:通过对比观察电流表示数,可以发现电流表示数一次比一次大,电路两端的电压 不变 ,可知电路中电阻 减小 。
不变
减小
实验结论:并联电路的总电阻的 阻值 比任何一个 分电阻阻值都小 。
理论推导:如图所示,设支路电阻分别为R1和R2,电路两端的电压为U。并联时,总电流等于 各支路电流之和 ,则有I=I1+I2,因为I=,I1=,I2=,所以=+,又因为在并联电路中,U=U1=U2,所以=+。
阻值
分电阻
阻值都小
各支路电流之和
若有n个电阻并联,则有=++…+,即并联电路的总电阻的 倒数 ,等于各并联电阻的 倒数之和 。
倒数
倒数之和
并联电阻的实质:几个电阻并联,相当于增大了电阻的 横截面积 ,因而总电阻 会变小(比最小的电阻还要小) ,有n个阻值为R0的 相同 电阻并联,其总电阻R= 。
横截
面积
会变小(比最小的电阻还要小)
相同
同课章节目录
