人教版八年级数学上册第12章《全等三角形》章节作业题(含答案)
文档属性
| 名称 | 人教版八年级数学上册第12章《全等三角形》章节作业题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 163.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 19:35:13 | ||
图片预览



文档简介
第12章《全等三角形》章节作业题
一、选择题
1.如图,是线段的中点,,使得,所添加的条件不正确的是( )
A. B. C. D.
2.如图,AC⊥BD于O,BO=OD,图中共有全等三角形( )对.
A.1对 B.2对 C.3对 D.4对
3.两个等腰三角形,若顶角和底边对应相等,则两个等腰三角形全等,其理由是( )
A.SAS B.SSS C.ASA D.ASA或AAS
4.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是120°,那么在△ABC中与这个120°的角对应相等的角是( )
A.∠A B.∠B C.∠C D.∠B或∠C
5.如图,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=2,则五边形ABCDE的面积为( )
A.2 B.3 C.4 D.5
6.如图,∠AOB的内部作射线OM,过点M分别作MA⊥OA于点A,MB⊥OB于点B,MA=MB,连接AB,若∠MAB=20°,则∠AOM的度数为( )
A.15° B.20° C.30° D.40°
二、填空题
7.如图,OP平分∠AOB,PB⊥OB,OA=8cm,PB=3cm,则△POA的面积等于 cm2.
8.在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是 .
9.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF= .
10.在中,为边上的高,,,则是 °.
11.如图,在△ABC中,AB的垂直平分线交BC于D,AC的中垂线交BC于E,∠BAC=124°,则∠DAE为 度.
12.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2= .
13.如图,△ABC≌△DEC,其中AB与DE是对应边,AC与DC是对应边,若∠A=∠30°,∠CEB=70°,则∠ACD= °.
14.如图,在中,AE是的角平分线,D是AE延长线上一点,于点H.若,,则 .
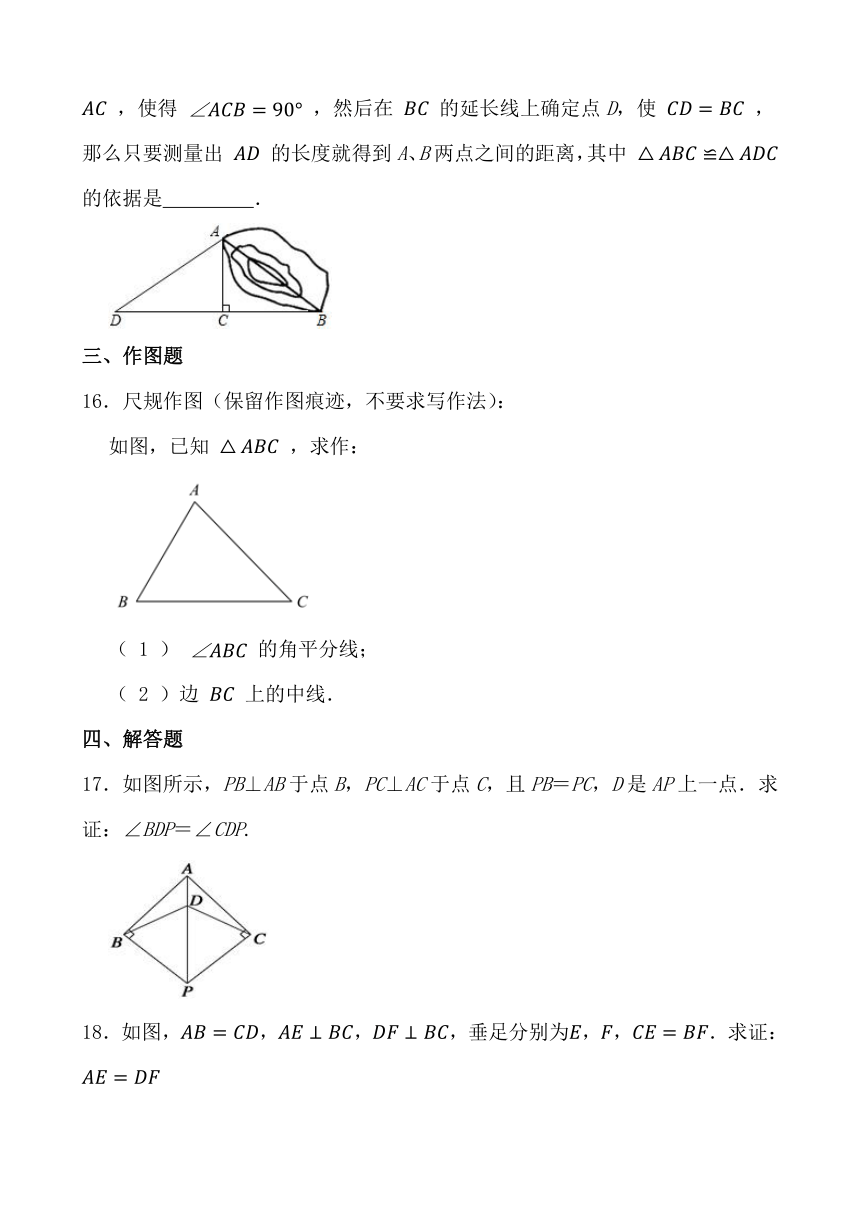
15.如图,为了测量A、B两点之间的距离,在地面上找到一点C,连接 、 ,使得 ,然后在 的延长线上确定点D,使 ,那么只要测量出 的长度就得到A、B两点之间的距离,其中 的依据是 .
三、作图题
16.尺规作图(保留作图痕迹,不要求写作法):
如图,已知 ,求作:
( 1 ) 的角平分线;
( 2 )边 上的中线.
四、解答题
17.如图所示,PB⊥AB于点B,PC⊥AC于点C,且PB=PC,D是AP上一点.求证:∠BDP=∠CDP.
18.如图,,,,垂足分别为,,.求证:
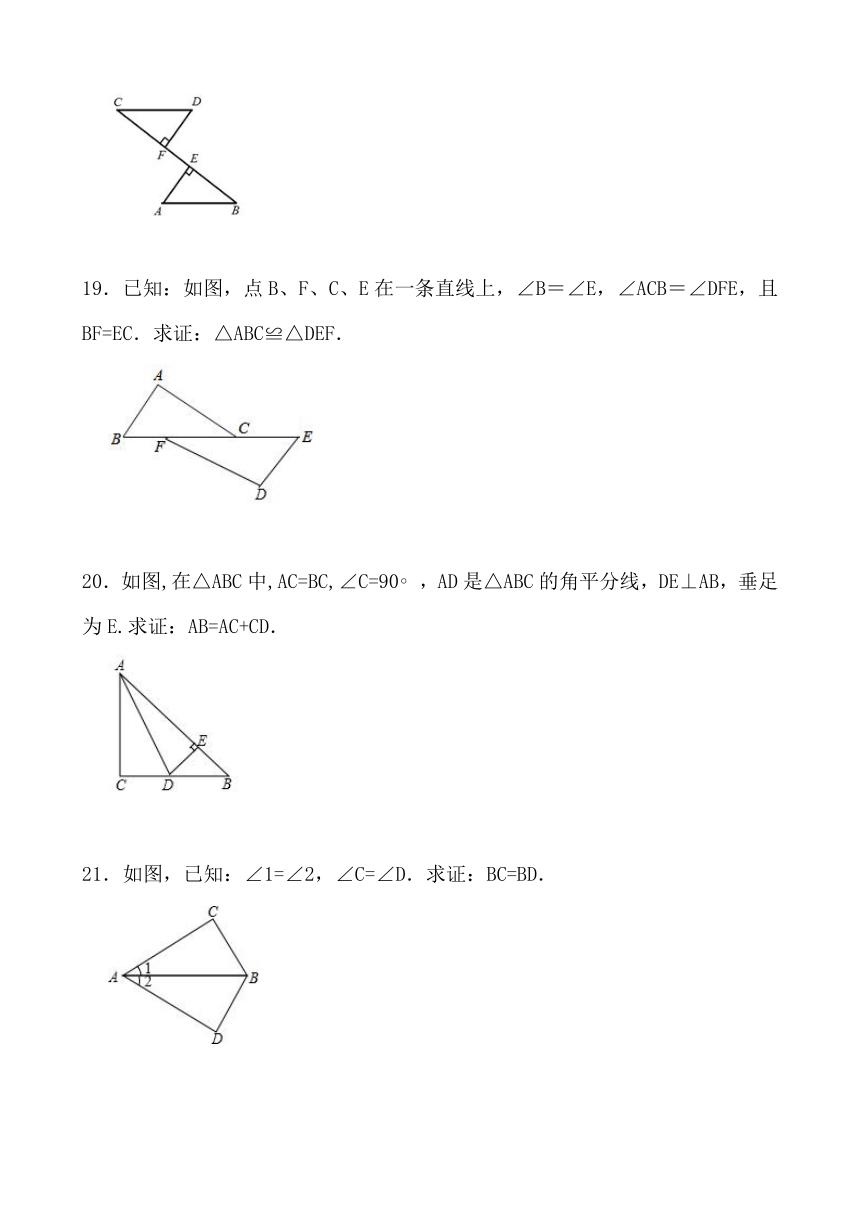
19.已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.
20.如图,在△ABC中,AC=BC,∠C=90 ,AD是△ABC的角平分线,DE⊥AB,垂足为E.求证:AB=AC+CD.
21.如图,已知:∠1=∠2,∠C=∠D.求证:BC=BD.
22.如图,两根旗杆相距12m,某人从B点沿BA走向A点,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,求:这个人从B点到M点运动了多长时间?
答案解析部分
1.A
2.C
3.D
4.A
5.C
6.B
7.12
8.15
9.2
10.80
11.68
12.180°
13.40
14.10°
15.
16.如图,射线BD、线段AE即为所求.
17.证明:∵PB⊥AB于点B,PC⊥AC于点C,∴∠ABP=∠ACP=90°.
在Rt△ABP和Rt△ACP中,∵ ,∴Rt△ABP≌Rt△ACP(HL),∴∠APB=∠APC.
在△PBD与△PCD中,∵ ,∴△PBD≌△PCD(SAS),∴∠BDP=∠CDP.
18.证明:,,垂足分别为,,
.
,
,
.
在和中,
,
,
.
19.解:∵AC∥DF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
20.证明:∵在△ABC中,AC=BC,∠C=90°,
∴∠ABC=45°,
又∵DE⊥AB,垂足为E,
∴∠B=∠EDB=45°,
∴DE=EB,
又∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴DE=CD.
在Rt△ACD与Rt△AED中,
∵ ,
∴△ACD≌△AED,
∴AC=AE,CD=DE,
∴AB=AE+EB=AC+CD.
21.证明:在△ABC和△ABD中,
∴△ABC≌△ABD(AAS),
∴BC=BD.
22.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°
∴∠CMA+∠ACM=90°,
∴∠ACM=∠DMB,
在Rt△ACM和Rt△BMD中,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴AC=BM=3m,
∴他到达点M时,运动时间为3÷1=3(s).
答:这个人从B点到M点运动了3s.
一、选择题
1.如图,是线段的中点,,使得,所添加的条件不正确的是( )
A. B. C. D.
2.如图,AC⊥BD于O,BO=OD,图中共有全等三角形( )对.
A.1对 B.2对 C.3对 D.4对
3.两个等腰三角形,若顶角和底边对应相等,则两个等腰三角形全等,其理由是( )
A.SAS B.SSS C.ASA D.ASA或AAS
4.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是120°,那么在△ABC中与这个120°的角对应相等的角是( )
A.∠A B.∠B C.∠C D.∠B或∠C
5.如图,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=2,则五边形ABCDE的面积为( )
A.2 B.3 C.4 D.5
6.如图,∠AOB的内部作射线OM,过点M分别作MA⊥OA于点A,MB⊥OB于点B,MA=MB,连接AB,若∠MAB=20°,则∠AOM的度数为( )
A.15° B.20° C.30° D.40°
二、填空题
7.如图,OP平分∠AOB,PB⊥OB,OA=8cm,PB=3cm,则△POA的面积等于 cm2.
8.在△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE交AC于D,垂足为E,则∠DBC的度数是 .
9.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF= .
10.在中,为边上的高,,,则是 °.
11.如图,在△ABC中,AB的垂直平分线交BC于D,AC的中垂线交BC于E,∠BAC=124°,则∠DAE为 度.
12.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2= .
13.如图,△ABC≌△DEC,其中AB与DE是对应边,AC与DC是对应边,若∠A=∠30°,∠CEB=70°,则∠ACD= °.
14.如图,在中,AE是的角平分线,D是AE延长线上一点,于点H.若,,则 .
15.如图,为了测量A、B两点之间的距离,在地面上找到一点C,连接 、 ,使得 ,然后在 的延长线上确定点D,使 ,那么只要测量出 的长度就得到A、B两点之间的距离,其中 的依据是 .
三、作图题
16.尺规作图(保留作图痕迹,不要求写作法):
如图,已知 ,求作:
( 1 ) 的角平分线;
( 2 )边 上的中线.
四、解答题
17.如图所示,PB⊥AB于点B,PC⊥AC于点C,且PB=PC,D是AP上一点.求证:∠BDP=∠CDP.
18.如图,,,,垂足分别为,,.求证:
19.已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.
20.如图,在△ABC中,AC=BC,∠C=90 ,AD是△ABC的角平分线,DE⊥AB,垂足为E.求证:AB=AC+CD.
21.如图,已知:∠1=∠2,∠C=∠D.求证:BC=BD.
22.如图,两根旗杆相距12m,某人从B点沿BA走向A点,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,求:这个人从B点到M点运动了多长时间?
答案解析部分
1.A
2.C
3.D
4.A
5.C
6.B
7.12
8.15
9.2
10.80
11.68
12.180°
13.40
14.10°
15.
16.如图,射线BD、线段AE即为所求.
17.证明:∵PB⊥AB于点B,PC⊥AC于点C,∴∠ABP=∠ACP=90°.
在Rt△ABP和Rt△ACP中,∵ ,∴Rt△ABP≌Rt△ACP(HL),∴∠APB=∠APC.
在△PBD与△PCD中,∵ ,∴△PBD≌△PCD(SAS),∴∠BDP=∠CDP.
18.证明:,,垂足分别为,,
.
,
,
.
在和中,
,
,
.
19.解:∵AC∥DF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
20.证明:∵在△ABC中,AC=BC,∠C=90°,
∴∠ABC=45°,
又∵DE⊥AB,垂足为E,
∴∠B=∠EDB=45°,
∴DE=EB,
又∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴DE=CD.
在Rt△ACD与Rt△AED中,
∵ ,
∴△ACD≌△AED,
∴AC=AE,CD=DE,
∴AB=AE+EB=AC+CD.
21.证明:在△ABC和△ABD中,
∴△ABC≌△ABD(AAS),
∴BC=BD.
22.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°
∴∠CMA+∠ACM=90°,
∴∠ACM=∠DMB,
在Rt△ACM和Rt△BMD中,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴AC=BM=3m,
∴他到达点M时,运动时间为3÷1=3(s).
答:这个人从B点到M点运动了3s.
