》高中数学》人教B版》人教B版必修5》第一章解直角三角形》正弦定理(校内公开课一等奖)
文档属性
| 名称 | 》高中数学》人教B版》人教B版必修5》第一章解直角三角形》正弦定理(校内公开课一等奖) |  | |
| 格式 | rar | ||
| 文件大小 | 401.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-01 19:37:00 | ||
图片预览





文档简介
课件18张PPT。学习目标:
1.理解正弦定理的推导过程。
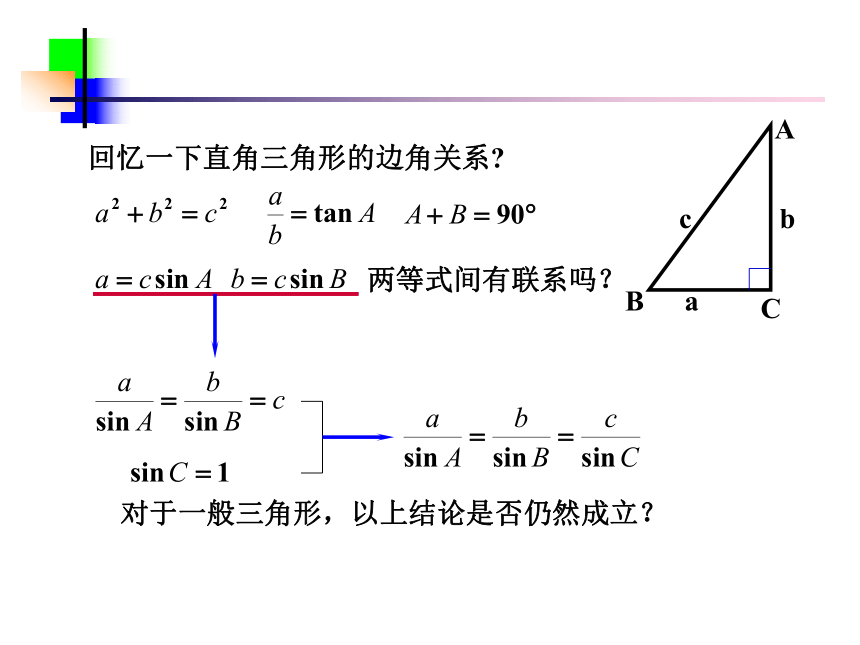
2.掌握正弦定理,并能运用正弦定理解斜三角形。两等式间有联系吗?对于一般三角形,以上结论是否仍然成立? △ABC中的三个内角∠A, ∠B, ∠C的对边,分别用a,b,c表示。
先看锐角△ABC(如图)
作CD⊥AB于点D,有
CD/b=sinA,即CD=bsinA;
CD/a=sinB,即CD=asinB;
因此bsinA=asinB,即
a/sinA=b/sinB.
同理可证a/sinA=c/sinC,
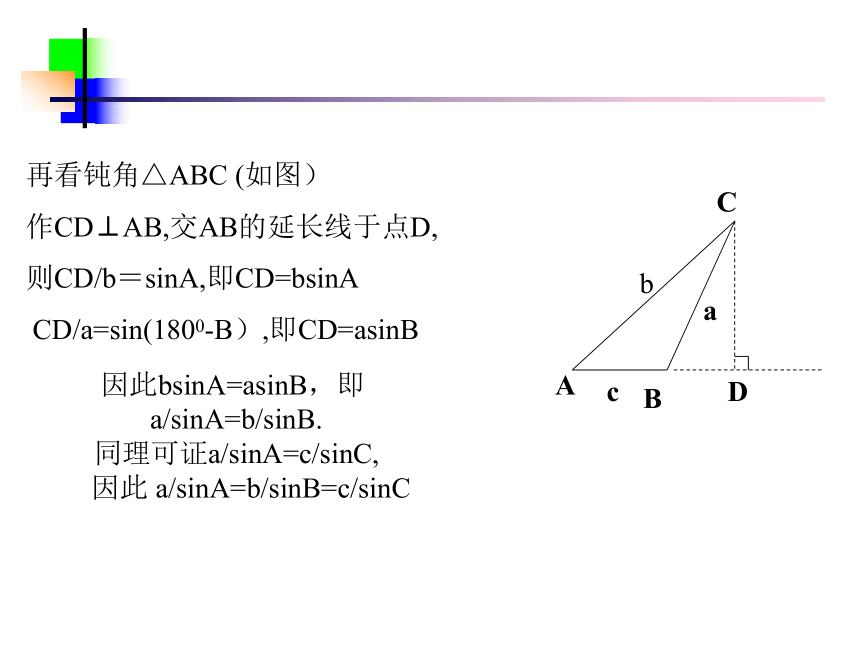
因此 a/sinA=b/sinB=c/sinC.CABabcD再看钝角△ABC (如图)
作CD⊥AB,交AB的延长线于点D,
则CD/b=sinA,即CD=bsinA
CD/a=sin(1800-B),即CD=asinB因此bsinA=asinB,即
a/sinA=b/sinB.
同理可证a/sinA=c/sinC,
因此 a/sinA=b/sinB=c/sinCCBbcaDA在一个三角形中,各边和它所对角的正弦的比相等,即=2R(R为外接圆半径)一般地,我们把三角形的三个角和它的对边分别叫做三角形的元素,已知三角形的几个元素求其他元素的过程叫做解三角形。利用正弦定理可以解决怎样的解三角形问题?已知两角和任一边,求其它两边和一角;AAS ASA
已知两边及其中一边对角,求另一边的对角及其他的边和角。SSA例题讲解练习:3=4解:在△ABC中,A=1800-(B+C)=450
在△ABC中,已知a=8, B=600,C=750,则b=_____∵∴b=
==例题讲解∴ A 为锐角 练习:在△ABC中,已知a=5 , c=10, A=300,则B=_____∵∴sinC=
==解:10sin3005=/2∵a < c ∴A < C∵A=300∴C=450或1350∴B=1050或150例题讲解巩固练习:C(2) 在△ABC中,若acosA=bcosB,判断这个三角形的形状解:∵a/sinA=b/sinB ∴a:b=sinA:sinB
又∵a/b=cosB/cosA ∴sinA/sinB=cosB/cosA∴sinAcosA=sinBcosB 即sin2A=sin2B ∴2A=2B或2A+2B=π∴A =B或A+B=π/2∴△ABC是等腰三角形或直角三角形巩固练习:∴ 等式成立小 结正弦定理用途:解斜三角形 已知两角和任一边,求其它两边和一角;
已知两边及其中一边对角,求另一边的对角及其他的边和角。实现三角形当中边角之间的转化作业 1、中, 2、中,谢谢
1.理解正弦定理的推导过程。
2.掌握正弦定理,并能运用正弦定理解斜三角形。两等式间有联系吗?对于一般三角形,以上结论是否仍然成立? △ABC中的三个内角∠A, ∠B, ∠C的对边,分别用a,b,c表示。
先看锐角△ABC(如图)
作CD⊥AB于点D,有
CD/b=sinA,即CD=bsinA;
CD/a=sinB,即CD=asinB;
因此bsinA=asinB,即
a/sinA=b/sinB.
同理可证a/sinA=c/sinC,
因此 a/sinA=b/sinB=c/sinC.CABabcD再看钝角△ABC (如图)
作CD⊥AB,交AB的延长线于点D,
则CD/b=sinA,即CD=bsinA
CD/a=sin(1800-B),即CD=asinB因此bsinA=asinB,即
a/sinA=b/sinB.
同理可证a/sinA=c/sinC,
因此 a/sinA=b/sinB=c/sinCCBbcaDA在一个三角形中,各边和它所对角的正弦的比相等,即=2R(R为外接圆半径)一般地,我们把三角形的三个角和它的对边分别叫做三角形的元素,已知三角形的几个元素求其他元素的过程叫做解三角形。利用正弦定理可以解决怎样的解三角形问题?已知两角和任一边,求其它两边和一角;AAS ASA
已知两边及其中一边对角,求另一边的对角及其他的边和角。SSA例题讲解练习:3=4解:在△ABC中,A=1800-(B+C)=450
在△ABC中,已知a=8, B=600,C=750,则b=_____∵∴b=
==例题讲解∴ A 为锐角 练习:在△ABC中,已知a=5 , c=10, A=300,则B=_____∵∴sinC=
==解:10sin3005=/2∵a < c ∴A < C∵A=300∴C=450或1350∴B=1050或150例题讲解巩固练习:C(2) 在△ABC中,若acosA=bcosB,判断这个三角形的形状解:∵a/sinA=b/sinB ∴a:b=sinA:sinB
又∵a/b=cosB/cosA ∴sinA/sinB=cosB/cosA∴sinAcosA=sinBcosB 即sin2A=sin2B ∴2A=2B或2A+2B=π∴A =B或A+B=π/2∴△ABC是等腰三角形或直角三角形巩固练习:∴ 等式成立小 结正弦定理用途:解斜三角形 已知两角和任一边,求其它两边和一角;
已知两边及其中一边对角,求另一边的对角及其他的边和角。实现三角形当中边角之间的转化作业 1、中, 2、中,谢谢
