平面直角坐标系

镇江实验学校八年级数学教学案
课题：4.3平面直角坐标系 （第1课时）
【学习目标】
1、领会实际模型中确定位置的方法，会正确画出平面直角坐标系。
2、会在给定的平面直角坐标系中，根据点的坐标描出点的位置，会由点的位置写出点的坐标。
【课前预习与导学】
1.如果班上第二列，第四行同学的位置记为（2，4），那么（4，5）表示谁的位置？（5，4）呢？
2．情境创设：
情境1：组织学生观察课本P123页的图片.音乐喷泉在中山北路西边50米,北京西路北边30米,你能确定音乐喷泉的位置吗 (课件演示) y
30
情境2：说说生活中如何确定某一目标的位置 20
【新知探索】 10
1）．情境1中如果将东西向的北京路和南北向的
中山路看成两条互相垂直的数轴,十字路口为这两 -50 -40 -30 -20 -10 0 x
条数轴的公共原点,那么“中山北路西边50米”可用数轴上的 表示；“北京西路北边30米”可用数轴上的 表示，这样音乐喷泉的位置就可以用有序实数对 来描述。
2）.有关概念:
构成平面直角坐标系,简称为 ,水平方向的数轴称为 或 ,竖直方向的数轴称为 或 ,它们统称为 .公共原点0称为 .
3）．平面直角坐标系中点的坐标.
①在直角坐标系中描出用有序实数对(2,-3)
所表示的点P
②如果Q是直角坐标系中的一点，你能找出
相应的一对有序实数吗？
③ 叫做点的坐标,
平面直角坐标系内的点与 一一对应.
如点P的坐标为（a,b）,记为 ，
其中a表示 坐标，b表示 坐标。
4）．平面直角坐标系中两条坐标轴把平面分成的4个区域称为 ，
按逆时针顺序分别记为 ，
坐标轴上的点 任何象限。 说出下图中各点所在的象限。
教师评价 家长签字
【例题讲解】
例1、画平面直角坐标系，并描出下列各点的位置：A(4,1),B(-2,4),C(-4,-2),D(3,-2),E(0,1),
F(-4,0)
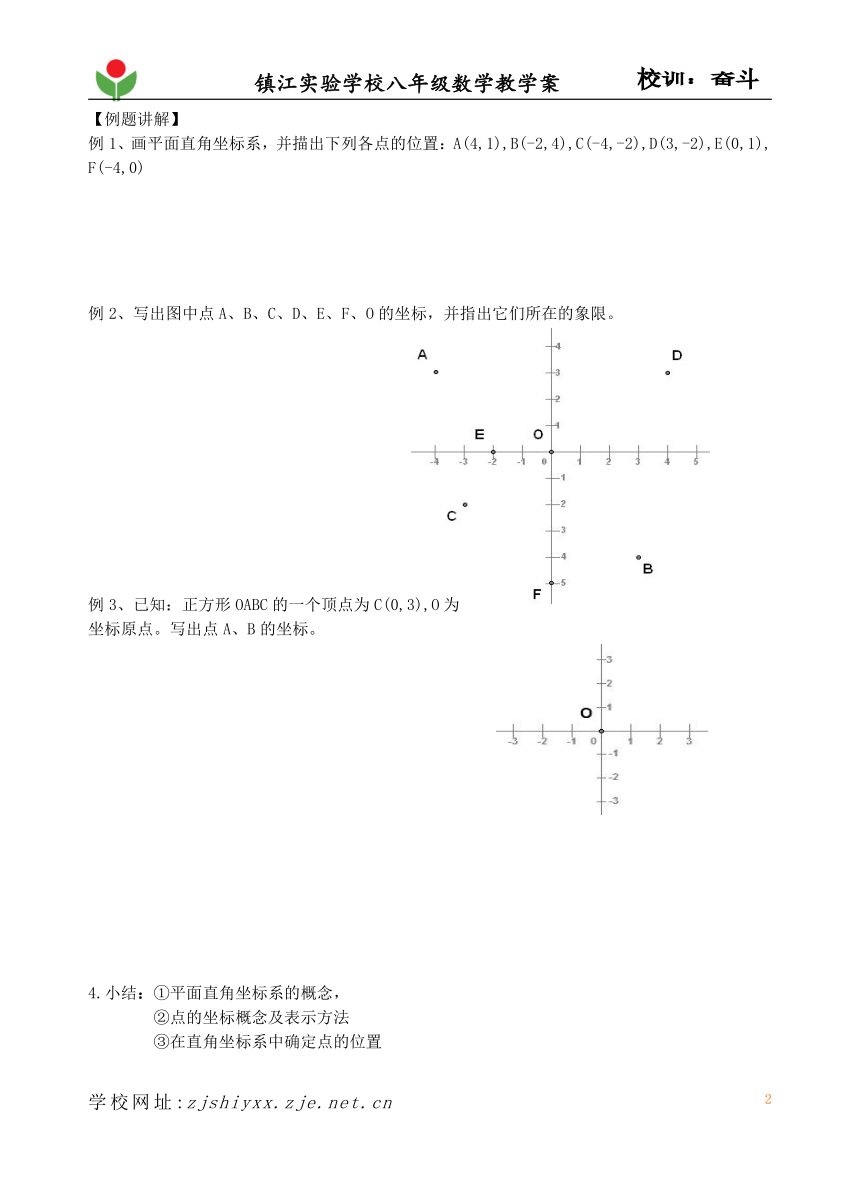
例2、写出图中点A、B、C、D、E、F、O的坐标，并指出它们所在的象限。
例3、已知：正方形OABC的一个顶点为C(0,3),O为
坐标原点。写出点A、B的坐标。
4.小结：①平面直角坐标系的概念，
②点的坐标概念及表示方法
③在直角坐标系中确定点的位置
【课堂检测】
1．如图，方格中填有16个英文字母，若D所在的方格用（1，1）表示，K所在的方格用（3，2）表示，则B所在的方格可用 表示，（2，3）表示方格中的字母是 ．
A E I M
B F J N
C G K O
D H L P
2、在平面直角坐标系中，已知点A（a,b）.
(1)若a、b同号，则点A可能在 象限。
（2）若a、b异号，则点A可能在 象限。
（3）若ab=0，则点A可能的位置是 。
3、点M(x,y)在第二象限，且，则点M的坐标是 ；若点M满足，则点M的坐标是 ，在第 象限。
4、已知点A在第四象限，它的横坐标与纵坐标的积为-6.点A的位置确定吗？若确定，请写出点A的坐标；若不确定，请写出2个符合上述条件的点的坐标。
【课后巩固】
1若点P在第四象限，且到x轴、y轴的距离分别为4和5，则点P的坐标为
2、已知某点在第二象限，其坐标是（x,y），若x+y=0,试写出2个满足条件的点
若x+y=5，试写出2个满足条件的点 。
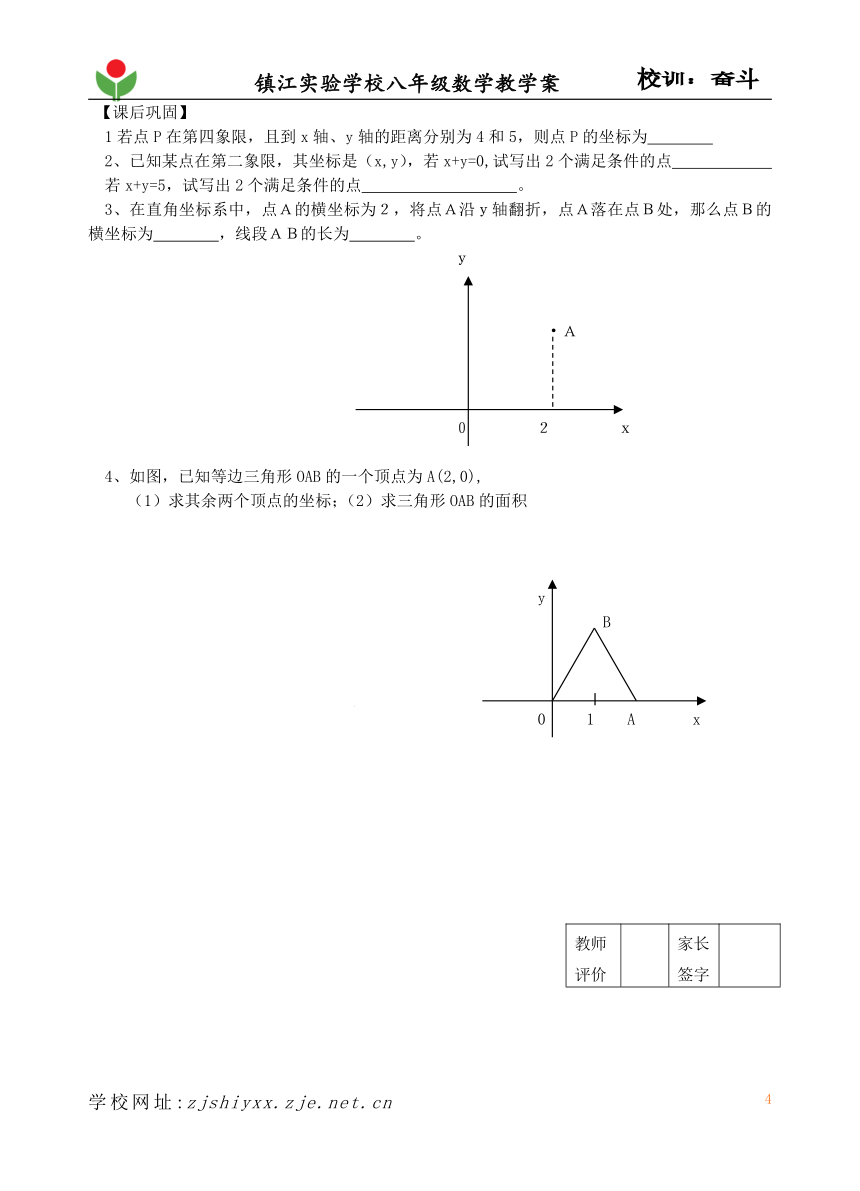
　3、在直角坐标系中，点Ａ的横坐标为２，将点Ａ沿ｙ轴翻折，点Ａ落在点Ｂ处，那么点Ｂ的横坐标为　　　　，线段ＡＢ的长为　　　　。
　　　　　　　　　　　　　　　　　　　　　　ｙ
　　　·Ａ
　　　　　　　　　　　　　　　　　　　　　　０　　　　２　　　　ｘ
　4、如图，已知等边三角形OAB的一个顶点为A(2,0),
　　（1）求其余两个顶点的坐标；（2）求三角形OAB的面积
y
B
0 1 A x
教师评价 家长签字
课题：4.3平面直角坐标系 （第２课时）
主备：罗永亮 课型：新授 审核：八年级数学组
班级 姓名 学号：
【学习目标】
在同一坐标系中探索对称点的坐标关系，强化对“点的坐标的数值变化与点的位置变化的关
系”的认识。
【课前预习与导学】
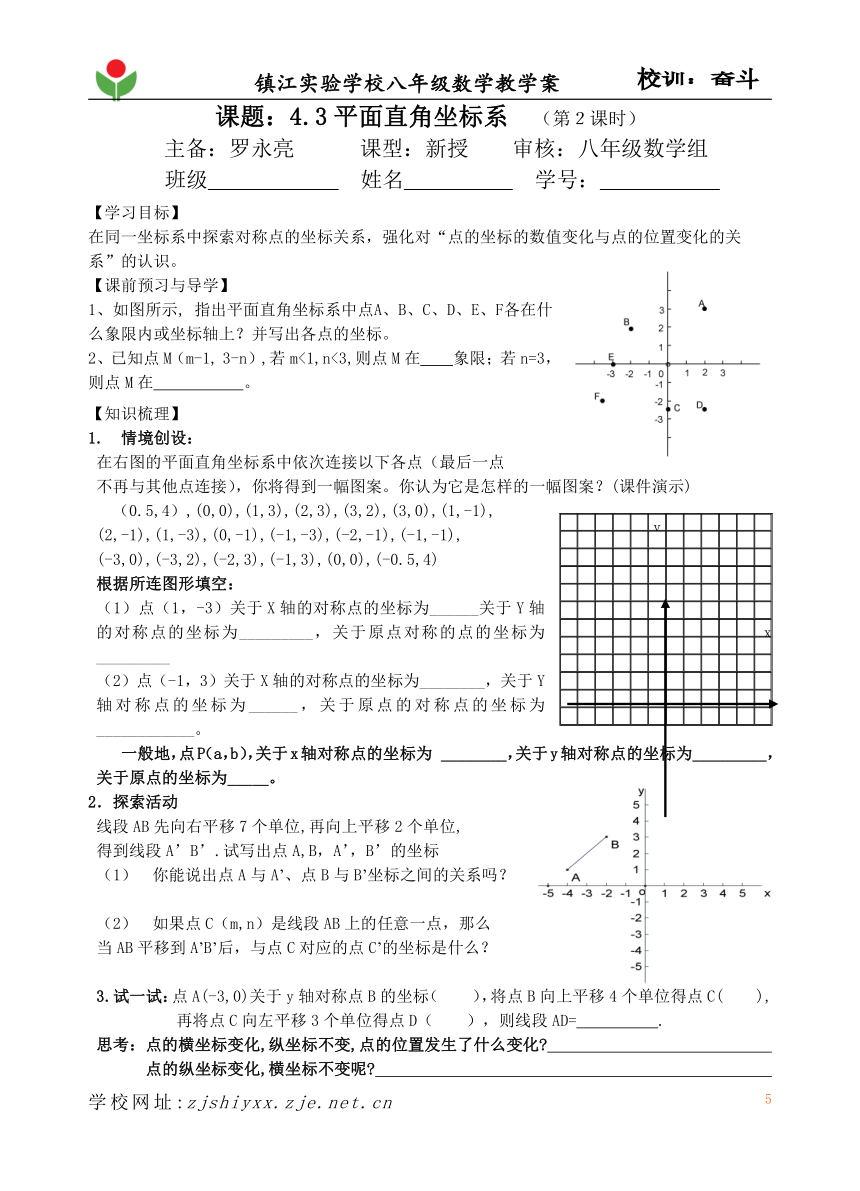
1、如图所示, 指出平面直角坐标系中点A、B、C、D、E、F各在什么象限内或坐标轴上？并写出各点的坐标。
2、已知点M（m-1, 3-n）,若m<1,n<3,则点M在 象限；若n=3，则点M在 。
【知识梳理】
y
x
1. 情境创设：
在右图的平面直角坐标系中依次连接以下各点（最后一点
不再与其他点连接），你将得到一幅图案。你认为它是怎样的一幅图案？(课件演示)
（0.5,4）,(0,0),(1,3),(2,3),(3,2),(3,0),(1,-1),
(2,-1),(1,-3),(0,-1),(-1,-3),(-2,-1),(-1,-1),
(-3,0),(-3,2),(-2,3),(-1,3),(0,0),(-0.5,4)
根据所连图形填空：
（1）点（1，-3）关于X轴的对称点的坐标为______关于Y轴的对称点的坐标为_________，关于原点对称的点的坐标为 _________
（2）点（-1，3）关于X轴的对称点的坐标为________，关于Y轴对称点的坐标为______，关于原点的对称点的坐标为____________。
一般地，点P（a，b），关于x轴对称点的坐标为 ________，关于y轴对称点的坐标为_________，关于原点的坐标为_____。
2．探索活动
线段AB先向右平移7个单位,再向上平移2个单位,
得到线段A’B’.试写出点A,B，A’，B’的坐标
（1） 你能说出点A与A’、点B与B’坐标之间的关系吗？
（2） 如果点C（m,n）是线段AB上的任意一点，那么
当AB平移到A’B’后，与点C对应的点C’的坐标是什么？
3.试一试：点A(-3,0)关于y轴对称点B的坐标（ ），将点B向上平移4个单位得点C( ),再将点C向左平移3个单位得点D（ ），则线段AD= .
思考：点的横坐标变化,纵坐标不变,点的位置发生了什么变化
点的纵坐标变化,横坐标不变呢
教师评价 家长签字
三、小结：1、对称点的坐标，2、点的平移
【例题讲解】
例1、ΔABC在平面直角坐标系中的位置如图所示：
y
A
4
B 2 C
4 2 0 2 4 6 x
2
4
(1) 将ΔABC向右平移4个单位得到ΔA1B1C1，
则点A1、B1的坐标分别是
（2）将ΔA1B1C1沿X轴翻折，得关于X轴对
称的ΔA2B2C2，则点A2、B2的坐标分别是
（3） 作ΔA1B1C1关于点O对称的ΔA3B3C3，则
点A3、B3的坐标分别为
此时ΔA2B2C2与ΔA3B3C3关于 对称。
例2、（1）点P（m,n）到x轴的距离为 ，到y轴的距离为 ；若点Q到x轴的距离为3，到y轴的距离为5，则点Q的坐标为
（2）若点A（5,3）、B(5,-1),则AB与 轴垂直，与 轴平行，且AB的长为 。
（3）已知点A(3,2)与点B(x,3x+1)在同一条垂直于x轴的直线上，且C是线段AB的中点。求点B与点C的坐标。
【课堂检测】
1、在直角坐标系中，点A(3,1)关于x轴对称的点的坐标是 ；关于y轴对称的点的坐标是 ；关于原点对称的点的坐标是 。
2、在直角坐标系中，描出点A(-2,3)，将点A向右平移3个单位得到点B，再将点B向下平移3个单位得到点C，则点B的坐标是 ，点C的坐标是 。
3、如图，在平面直角坐标系中，□ABCD的顶点Ａ、Ｂ、Ｄ的坐标分别是（０，０），（５，０），（２，３），则顶点Ｃ的坐标是　　　　　　　　　　（　　　　）
Ａ.(３,７)　　　Ｂ.(５,３)　　　　　　ｙ
Ｃ.(７,３)　　　Ｄ.(８,２)　　　　　　　　Ｄ　　　　　Ｃ
　　　　　　　　　　　　　　　　　　　 ０(Ａ)　　Ｂ　　　　ｘ
　　　　　　　　　　　　　　　　　　
4、如图，已知等边三角形ABC的两个顶点的坐标分别为A（-4，0），B(2,0)
(1)求点C的坐标
（2）求该三角形的面积
【课后巩固】
1、已知点A坐标为（a,5），点B的坐标为（3，b），如果A、B关于x轴对称，那么
a= ,b= ；如果A、B关于y轴对称，那么a= ,b= ；如果A、
B关于原点对称，那么a= ,b= ；如果线段AB与x轴平行，且AB=2，那么，
a= ,b=
2、已知矩形ABCD中，点A、B、C的坐标分别为（0，0）、（5，0）、（5，3），则点D的坐标
为
3、若点P到x轴的距离为2，到y轴的距离为3，则点P的坐标为 。
4、四边形ABCD的顶点坐标分别为A(1,-2)、B(5,-4)、C(4,-1)、D(3,-1),把四边形ABCD向左平
移3个单位，再向上平移4个单位，得到四边形A′B′C′D′,请在同一平面直角坐标系中画出这
两个四边形，并写出点A′、B′、C′、D′的坐标。
*5、在直角坐标系中，顺次连接A(4,0)、B(1,-1)、C(7,-1),你知道ΔABC是怎样的三角形吗？
通过移动点A，可使三角形ABC成为等腰直角三角形吗？你有几种移法。
教师评价 家长签字
课题：4.3平面直角坐标系 （第3课时）
主备：罗永亮 课型：新授 审核：八年级数学组
班级 姓名 学号：
【学习目标】
1、 能根据已知条件，建立适当的直角坐标系，描述物体的位置，写出点的坐标。
2、 经历对同一个问题建立不同直角坐标系的过程，体会数形结合的解题思想。
【课前预习与导学】
1、点M(4,0)到点(-1,0)距离是 ；点P（-5，12）到x轴的距离是 ，到y轴的距离是 ，到原点的距离是 。
2、点P(m,-2m)是第二象限的点，则m的取值范围是 。
3、点A(a,b)关于x轴的对称点A1( ),关于y轴的对称点A2（ ）, 关于原点的对称点A3（ ）。
4、在直角坐标系中，点A(3,-2)、B((3,1)、C(3,4)是否共线？ ；线段AB BC(填<、=、>)
【知识梳理】
尝试与探索：
1、如图，站在中心广场，你能根据这张旅游景点分
布图，说出各旅游景点的位置吗？（用坐标表示）
2、电视机厂通过电脑控制的机械手,把各种元件准确插入线路板的孔眼中,然后通过焊接工序将它们焊牢.如果你是工程师,那么你是怎样向机械手下达指令,让它把元件准确插入相应的孔眼中 说说你的办法。
教师评价 家长签字
【例题讲解】
例1、如图，已知正方形ABCD的边长为4，①建立适当的直角坐标系，写出各顶点的坐标。
D C
A B
②还能建立不同的直角坐标系，表示
正方形各顶点的坐标吗？画图说明。
③若要使点A的坐标是（1，1），B（5，1），
你能画出直角坐标系吗？若能，请写出
其他两个点的坐标？ D C
A B
例2、如图，在梯形ABCD中，∠A=∠B=90°, ∠C=45°,AD=3,BC=5.建立适当的直角坐标系并写出各个定点的坐标。
A D
B C
【课堂检测】
1、把点P（3，-2）沿X轴方向向 平移 个单位得到点A（5，-2），把点P（3，-2）沿Y轴方向向 平移 个单位得到点A（3，1）
2、点A（5，-2）到X轴的距离为 ，到Y轴的距离为 ，到原点轴的距离为 。
3、根据某动物园的平面示意图，以大门为坐标原点，以正东方为x轴正方向、正北方为y轴正方向，以1cm为单位长度，建立平面
直角坐标系，用坐标表示猴山、驼峰、
百鸟园和熊猫馆的位置。
4、 已知等边三角形ABC的边长为2，建立适当的平面直角坐标系，写出各顶点的坐标。
【课后巩固】
1、点A（a+1,-4)与B(2,b+3)所在的直线与X轴平行，则a ,b ；所在的直线与Y轴平行，则a ,b ；点A在第一、三象限的角平分线上，则a= ;点B在第二、四象限的角平分线上，则b= ；
2、如图，在ΔABC中，AC=CB=BA=6,CD是边AB上的高。建立适当的直角坐标系并写出各个顶点的坐标。
A D B
C
3、 已知菱形ABCD的两条对角线的长度分别为6和8，建立适当的直角坐标系，并写出各顶点的坐标。
*4、如图，在平面直角坐标系中，A（-3，4）、B（-1， 2），O为坐标原点。求ΔAOB的面积。
教师评价 家长签字
课题：第四章复习
主备：罗永亮 课型：复习 审核：八年级数学组
班级 姓名 学号：
【学习目标】
1、 进一步理解表格、图形和式子所揭示的数量变化的规律及变化的数量间的相互关系。
2、 进一步领会点的位置变化有时可以用数量的变化来描述，数量的变化有时可以用点的位置变化来说明。
3、 进一步感受平面直角坐标系是研究和解决一些实际问题的有力工具。
4、 【知识结构梳理】
1、描述数量变化、位置变化及其关系的常用方式有 、 、
2、
3、小结点的坐标
（1）点P（a,b)到X轴的距离是︱b︱，到Y轴的距离是︱a︱,到原点的距离是
（2）对称性 1）关于X轴对称的两点横坐标相等，纵坐标互为相反。
2）关于Y轴对称的两点横坐标互为相反，纵坐标相等。
3）关于原点轴对称的两点横坐标互为相反，纵坐标互为相反。
（3）平行：
1）两点的横坐标相等，纵坐标不相等，则这两点所在的直线与Y轴平行，与X轴垂直。
2）两点的横坐标不相等，纵坐标相等，则这两点所在的直线与X轴平行，与Y轴垂直。
【基础训练】
1、点P（-3，4）与X轴对称的点的坐标为 ；与Y轴对称的点的坐标为 ；与原点对称的点的坐标为 。
2、点A（6，-3）到X轴的距离为 ，到Y轴的距离为 ，到原点轴的距离为 。
3、点A（a,-4)与B(2,b)所在的直线与X轴平行，则a= ,b= ；若所在的直线与Y轴平行，则a= ,b= .
4、点A（a,b)在第一、三象限的角平分线上，则a、b的关系是 ；在第二、四象限的角平分线上，则a、b的关系是 。
5、已知点A（1+m，2m+1）在x轴上，则m= ，此时坐标为
6、若点P（m，n）在第三象限，则点Q（-m， n）在 象限，
7、一辆汽车行驶的路程与行驶时间的关系（如图），下列说法中，正确的是（ ）
（A）前3h中汽车的速度越来越快 路程/km
（B）3h后汽车静止不动
（C）3h后汽车以相同的速度行驶
（D）前3h汽车以相同的速度行驶
0 3 5 时间/km
【例题讲解】
例1、已知点A（6，2），B（2，－4）。求△AOB的面积.
例2、如图，菱形的边长为6，一个内角为60°，试建立一个适当的直角坐标系，使得菱形的4个顶点坐标容易求出。
例3、在直角坐标系中，已知点A（1，2），B（1，6），C（0， 4）.
(1)试判断四边形OABC的形状并求其面积；（2）若O、C两点不动，使四边形OABC变成面积为4的矩形，则线段AB将如何变化？求出变化后的A、B两点的坐标；（3）若O、C两点不动，使四边形OABC变成正方形，则线段AB将如何变化？求出变化后的A、B两点的坐标；
【课堂检测】
1、在直角坐标系中，点P（1，3）向下平移4个单位长度后的坐标为（ ）
2、若点A（a-1,a）在第二象限，则点B（a，1-a）在第 象限。
3已知点A（5，2）和点B（-3，b），且AB∥x轴，则b= 。
4、点A在第三象限，点A到x轴的距离为4，点A到y轴的距离为3，那么点A的坐标为（ ）
5、如图，若将△ABC绕点C顺时针旋转90°后得到△A1B1 C1。则A点的对应点A1 的坐标是（ ）
B点的对应点B1 的坐标是（ ）
s/km A
B
C
t/min
6、如上图，纵轴表示小王与小李家的距离，小王从A点离家出发（虚线），小李从B点离家出发（实线）。
（1）小王与小李谁先离家？（2）图中虚线与实线合在一起的部分表示什么？
（3）小王与小李各走了多少时间？他们最后到了什么地方？
7、平行四边形两个顶点的坐标分别为（-3，0）、（1，0），第三个顶点在y轴上，且与x轴的距离为3个单位长度。求第四个顶点的坐标。
【课后巩固】
1、将点P（-5，3）向右平移5个单位，再向下平移3个单位，得到点Q（h，t），则h= ，t= 。
2、已知点A（ 1，-2）与位于第三象限的点B（x，y）的连线平行与x轴，且点B到点A的距离等于2，则x= y= 。
3、点P（x，y）在第二象限，且 =5， =3,则P点关于原点对称的点的坐标是
4、已知点P（x，y）满足方程（x-2)2+ =0。则点P关于x轴对称的点的坐标是 。
5、点P（x，y）满足 xy＞0, x ＋y＞0，则点P在 象限。
6、在如图所示的平面直角坐标系中，圆的圆心P的坐标为(2,0)，圆的半径为3。求圆与坐标轴的交点A、B、C、D的坐标。
7、如图，在直角坐标系中，AD=8,OD=OB,□ABCD的面积为24.求平行四边形4个顶点的坐标。
y
B C
A 0 D x
8、如图，在ΔABC中，∠BAC=120°，AB=AC,BC=4,请你建立适当的直角坐标系，并写出A、B、C各点的坐标 A
B C
教师评价 家长签字
·
-4
-2-2
-4444
-2
4
22
4
x
关于原点对称点
关于y轴对称点
关于x轴对称点
第四象限 (＋，－)
第三象限 (－，－)
第二象限 (－，＋)
第一象限 (＋，＋)
象限
y轴（纵轴）(0,b)
坐标原点 (0,0)
x轴（横轴）(a,0)
坐标轴
点(a，b)的对称性
组成
平面直角坐标系
22
60°
6
B
A
-4
-2
-4
-2
4
2
4
2
O
y
o
yy
xx
D
P
C
B
A
y
x
0
PAGE
16
学校网址: