人教版七年级数学上册第二章《整式的加减》期末复习题 (2)(含答案)
文档属性
| 名称 | 人教版七年级数学上册第二章《整式的加减》期末复习题 (2)(含答案) | 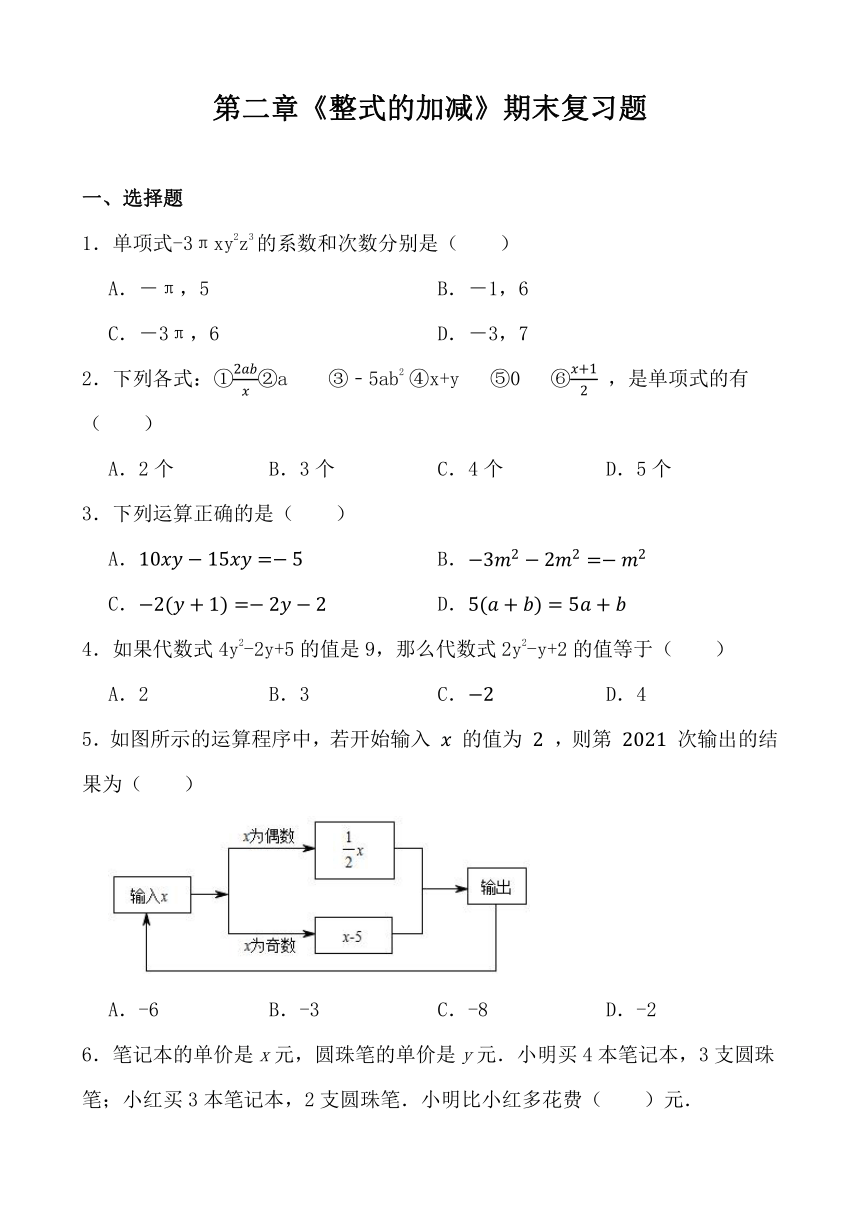 | |
| 格式 | docx | ||
| 文件大小 | 65.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-03 20:26:33 | ||
图片预览



文档简介
第二章《整式的加减》期末复习题
一、选择题
1.单项式-3πxy2z3的系数和次数分别是( )
A.-π,5 B.-1,6
C.-3π,6 D.-3,7
2.下列各式:①②a ③﹣5ab2 ④x+y ⑤0 ⑥ ,是单项式的有( )
A.2个 B.3个 C.4个 D.5个
3.下列运算正确的是( )
A. B.
C. D.
4.如果代数式4y2-2y+5的值是9,那么代数式2y2-y+2的值等于( )
A.2 B.3 C. D.4
5.如图所示的运算程序中,若开始输入 的值为 ,则第 次输出的结果为( )
A.-6 B.-3 C.-8 D.-2
6.笔记本的单价是x元,圆珠笔的单价是y元.小明买4本笔记本,3支圆珠笔;小红买3本笔记本,2支圆珠笔.小明比小红多花费( )元.
A.x﹣y B.x+y C.x+5y D.7x+5y
二、填空题
7.多项式 是 次 项式.
8.若与的和仍是一个单项式,则 .
9.一个长方形的一边长 米,另一边比它短 米,则这个长方形的周长为 .
10.若x2+x+1的值是4,则3x2+3x+6的值是 .
11.将n张长度为10 cm的纸条,一张接一张地黏成一张长纸条,黏合部分的长度都是3 cm,则这张黏合后的长纸条总长是 cm(用含n的代数式表示).
12.一个两位数,个位数字是十位数字的2倍,若个位数字为a,则这个两位数可表示为
13.如图,用灰白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖数为 .
三、解答题
14.合并同类项:
(1)x2+3x2+x2-3x2;
(2)3a2-1-2a-5+3a-a2.
15.先化简,再求值:2﹣3(a2﹣2a)+2(﹣3a2+a+1),其中a=﹣2.
16.有一道题目是一个多项式加上2a2-3a+5,李明误当成了减法计算,结果得到a2-5a+7,则正确的结果应该是什么?
17.已知多项式 是六次四项式,单项式 的次数与这个多项式的次数相同.求: 的值.
18. 如图,一个窗户的上部是由四个扇形组成的一个半径为a的半圆,下部是边长相同的四个小正方形,请计算这个窗户的面积和窗户外框的总长.
19.某公园出售的一次性使用门票,每张10元,为了吸引更多游客,新近推出购买“个人年票”的售票活动(从购买日起,可供持票者使用一年).年票分A、B两类:
A类年票每张100元,持票者每次进入公园无需再购买门票;
B类年票每张50元,持票者进入公园时需再购买每次2元的门票.
(1)某游客中一年进入该公园共有n次,
如果不购买年票,则一年的费用为 元;
如果购买A类年票,则一年的费用为 元;
如果购买B类年票,则一年的费用为 元;(用含n的代数式表示)
(2)假如某游客一年中进入该公园共有12次,选择哪种购买方式比较优惠?请通过计算说明理由.
(3)某游客一年中进入该公园n次,他选择购买哪一类年票合算?请你帮助他决策,并说明你的理由.
答案解析部分
1.C
2.B
3.C
4.D
5.A
6.B
7.五;四
8.-2
9.(6a-6b)米
10.15
11.(7n+3)
12.6a
13.3n+2
14.(1)解:原式=(1+3+1-3)x2
=2x2.
(2)解:原式=(3-1)a2+(3-2)a+(-1-5)
=2a2+a-6.
15.解:原式=2﹣3a2+6a﹣6a2+2a+2
=﹣9a2+8a+4,
当a=﹣2时,
原式=﹣9×(﹣2)2+8×(﹣2)+4
=﹣9×4﹣16+4
=﹣36﹣16+4
=﹣48.
16.解:
解:由题意可得,多项式为:2a2-3a+5+a2-5a+7=3a2-8a+12,
则正确的结果为:3a2-8a+12+2a2-3a+5=5a2-11a+17.
答:正确的结果为5a2-11a+17.
17.解:∵多项式 是六次四项式,∴2+m+1=6,解得:m=3.
又∵单项式4.5x2ny5﹣m的次数也为6,∴2n+5﹣m=6,解得:n=2,
故可得:m2+n2= 32+22=13.
18.解:由题意知,四个小正方形的边长均为a,
则窗户的面积S=+4a2;
窗户外框的总长=πa+6a.
19.(1)10n;100;50+2n
(2)解:假如某游客一年进入公园共有12次, 则不购买年票的费用为10×12=120(元), 购买A类年票的费用为100元, 购买B类年票的费用为50+2×12=74(元); 则购买B类年票比较优惠
(3)解:50+2n﹣100=2n﹣50, 当n=25时,选择A、B类年票的费用相同; 当n<25时,购买B类年票比较合算; 当n>25时,购买A类年票比较合算.
一、选择题
1.单项式-3πxy2z3的系数和次数分别是( )
A.-π,5 B.-1,6
C.-3π,6 D.-3,7
2.下列各式:①②a ③﹣5ab2 ④x+y ⑤0 ⑥ ,是单项式的有( )
A.2个 B.3个 C.4个 D.5个
3.下列运算正确的是( )
A. B.
C. D.
4.如果代数式4y2-2y+5的值是9,那么代数式2y2-y+2的值等于( )
A.2 B.3 C. D.4
5.如图所示的运算程序中,若开始输入 的值为 ,则第 次输出的结果为( )
A.-6 B.-3 C.-8 D.-2
6.笔记本的单价是x元,圆珠笔的单价是y元.小明买4本笔记本,3支圆珠笔;小红买3本笔记本,2支圆珠笔.小明比小红多花费( )元.
A.x﹣y B.x+y C.x+5y D.7x+5y
二、填空题
7.多项式 是 次 项式.
8.若与的和仍是一个单项式,则 .
9.一个长方形的一边长 米,另一边比它短 米,则这个长方形的周长为 .
10.若x2+x+1的值是4,则3x2+3x+6的值是 .
11.将n张长度为10 cm的纸条,一张接一张地黏成一张长纸条,黏合部分的长度都是3 cm,则这张黏合后的长纸条总长是 cm(用含n的代数式表示).
12.一个两位数,个位数字是十位数字的2倍,若个位数字为a,则这个两位数可表示为
13.如图,用灰白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖数为 .
三、解答题
14.合并同类项:
(1)x2+3x2+x2-3x2;
(2)3a2-1-2a-5+3a-a2.
15.先化简,再求值:2﹣3(a2﹣2a)+2(﹣3a2+a+1),其中a=﹣2.
16.有一道题目是一个多项式加上2a2-3a+5,李明误当成了减法计算,结果得到a2-5a+7,则正确的结果应该是什么?
17.已知多项式 是六次四项式,单项式 的次数与这个多项式的次数相同.求: 的值.
18. 如图,一个窗户的上部是由四个扇形组成的一个半径为a的半圆,下部是边长相同的四个小正方形,请计算这个窗户的面积和窗户外框的总长.
19.某公园出售的一次性使用门票,每张10元,为了吸引更多游客,新近推出购买“个人年票”的售票活动(从购买日起,可供持票者使用一年).年票分A、B两类:
A类年票每张100元,持票者每次进入公园无需再购买门票;
B类年票每张50元,持票者进入公园时需再购买每次2元的门票.
(1)某游客中一年进入该公园共有n次,
如果不购买年票,则一年的费用为 元;
如果购买A类年票,则一年的费用为 元;
如果购买B类年票,则一年的费用为 元;(用含n的代数式表示)
(2)假如某游客一年中进入该公园共有12次,选择哪种购买方式比较优惠?请通过计算说明理由.
(3)某游客一年中进入该公园n次,他选择购买哪一类年票合算?请你帮助他决策,并说明你的理由.
答案解析部分
1.C
2.B
3.C
4.D
5.A
6.B
7.五;四
8.-2
9.(6a-6b)米
10.15
11.(7n+3)
12.6a
13.3n+2
14.(1)解:原式=(1+3+1-3)x2
=2x2.
(2)解:原式=(3-1)a2+(3-2)a+(-1-5)
=2a2+a-6.
15.解:原式=2﹣3a2+6a﹣6a2+2a+2
=﹣9a2+8a+4,
当a=﹣2时,
原式=﹣9×(﹣2)2+8×(﹣2)+4
=﹣9×4﹣16+4
=﹣36﹣16+4
=﹣48.
16.解:
解:由题意可得,多项式为:2a2-3a+5+a2-5a+7=3a2-8a+12,
则正确的结果为:3a2-8a+12+2a2-3a+5=5a2-11a+17.
答:正确的结果为5a2-11a+17.
17.解:∵多项式 是六次四项式,∴2+m+1=6,解得:m=3.
又∵单项式4.5x2ny5﹣m的次数也为6,∴2n+5﹣m=6,解得:n=2,
故可得:m2+n2= 32+22=13.
18.解:由题意知,四个小正方形的边长均为a,
则窗户的面积S=+4a2;
窗户外框的总长=πa+6a.
19.(1)10n;100;50+2n
(2)解:假如某游客一年进入公园共有12次, 则不购买年票的费用为10×12=120(元), 购买A类年票的费用为100元, 购买B类年票的费用为50+2×12=74(元); 则购买B类年票比较优惠
(3)解:50+2n﹣100=2n﹣50, 当n=25时,选择A、B类年票的费用相同; 当n<25时,购买B类年票比较合算; 当n>25时,购买A类年票比较合算.
