6.3反比例函数的应用 作业 (含答案)2023--2024学年北师大版九年级数学上册
文档属性
| 名称 | 6.3反比例函数的应用 作业 (含答案)2023--2024学年北师大版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 274.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 09:02:01 | ||
图片预览


文档简介
单元 名称 反比例函数 课题 反比例函数的应用 节次 1课时
作业类型 作业内容 设计意图、设计依据、 参考答案
课堂作业 1.随着新业态兴起和深圳市民出行习惯的改变,电动自行车已经成为当下重要的交通工具.已知电动自行车蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系().下列反映电流I与电阻R之间函数关系的图象大致是( ) (主要对应单元目标:910610) 意图:通过对生活中实际问题电流、电压、电阻函数关系的考察,巩固反比例函数的概念、图象和性质. 题源:改编自2023年湖北省荆州市中考试卷第4题. 答案:B ∵电流I与电阻R是反比例函数关系(),R、I均大于0, ∴反映电流I与电阻R之间函数关系的图象大致是B选项,故选:B.
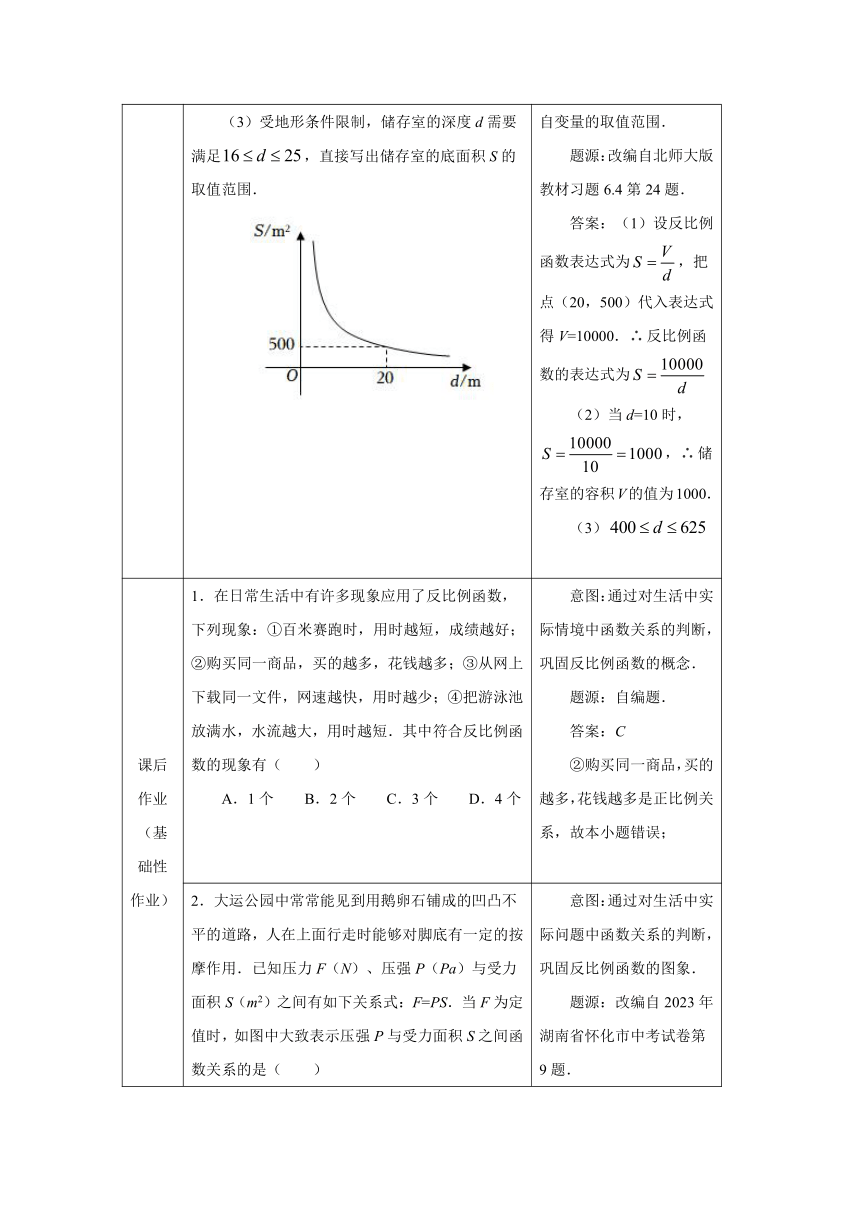
2.龙岗燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2)与其深度d(单位:m)是反比例函数关系,它的图象如图所示. (1)写出这一函数的表达式; (2)当深度为10 m时,求储存室的容积V的值; (3)受地形条件限制,储存室的深度d需要满足,直接写出储存室的底面积S的取值范围. 意图:通过阅读材料,对天然气储存室的底面积和深度之间函数关系的实际问题的考查,巩固反比例函数概念和性质、用待定系数法求函数表达式,会求出函数值和确定实际问题中自变量的取值范围. 题源:改编自北师大版教材习题6.4第24题. 答案:(1)设反比例函数表达式为,把点(20,500)代入表达式得V=10000.∴反比例函数的表达式为 (2)当d=10时,,∴储存室的容积V的值为1000. (3)
课后作业 (基础性作业) 1.在日常生活中有许多现象应用了反比例函数,下列现象:①百米赛跑时,用时越短,成绩越好;②购买同一商品,买的越多,花钱越多;③从网上下载同一文件,网速越快,用时越少;④把游泳池放满水,水流越大,用时越短.其中符合反比例函数的现象有( ) A.1个 B.2个 C.3个 D.4个 意图:通过对生活中实际情境中函数关系的判断,巩固反比例函数的概念. 题源:自编题. 答案:C ②购买同一商品,买的越多,花钱越多是正比例关系,故本小题错误;
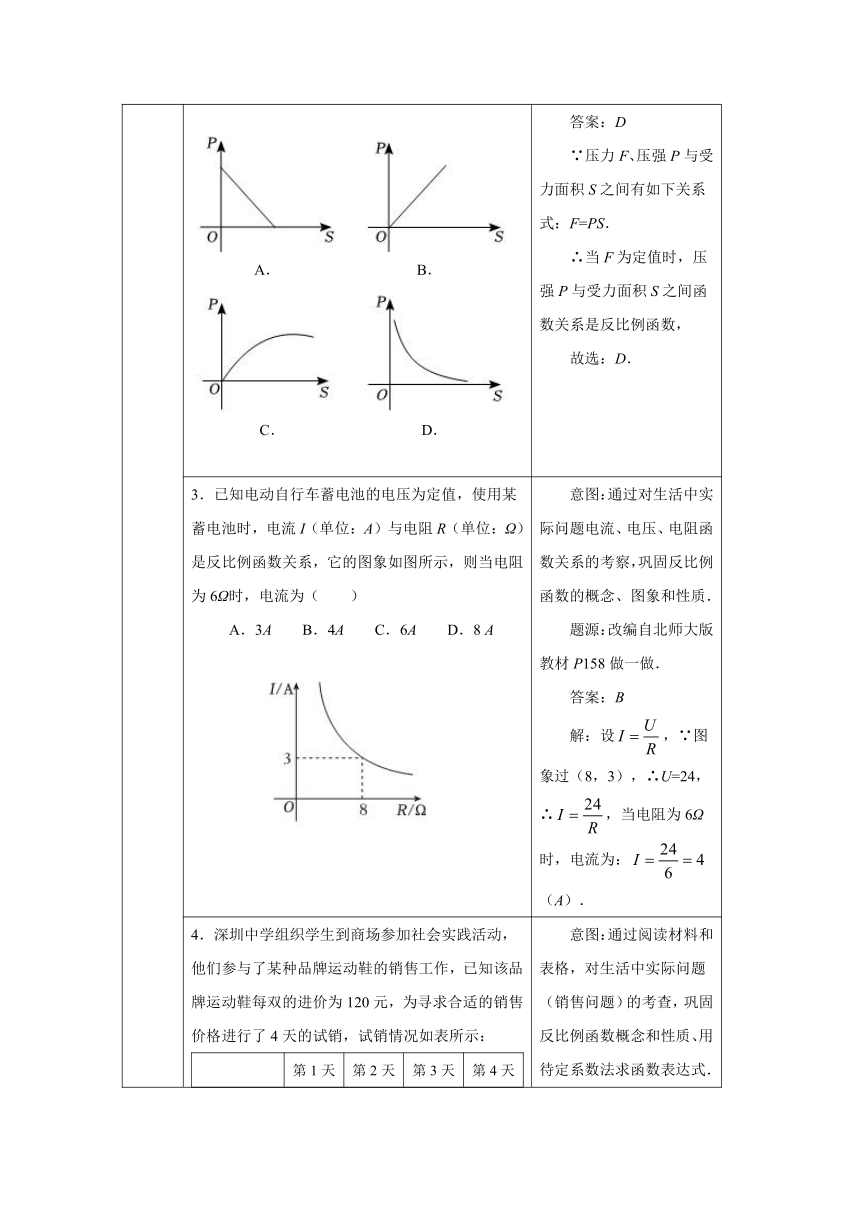
2.大运公园中常常能见到用鹅卵石铺成的凹凸不平的道路,人在上面行走时能够对脚底有一定的按摩作用.已知压力F(N)、压强P(Pa)与受力面积S(m2)之间有如下关系式:F=PS.当F为定值时,如图中大致表示压强P与受力面积S之间函数关系的是( ) 意图:通过对生活中实际问题中函数关系的判断,巩固反比例函数的图象. 题源:改编自2023年湖南省怀化市中考试卷第9题. 答案:D ∵压力F、压强P与受力面积S之间有如下关系式:F=PS. ∴当F为定值时,压强P与受力面积S之间函数关系是反比例函数, 故选:D.
3.已知电动自行车蓄电池的电压为定值,使用某蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则当电阻为6Ω时,电流为( ) A.3A B.4A C.6A D.8 A 意图:通过对生活中实际问题电流、电压、电阻函数关系的考察,巩固反比例函数的概念、图象和性质. 题源:改编自北师大版教材P158做一做. 答案:B 解:设,∵图象过(8,3),∴U=24,∴,当电阻为6Ω时,电流为:(A).
4.深圳中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该品牌运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示: 第1天第2天第3天第4天售价x/元150200250300销售量y/双40302420
(1)表中数据, x与y满足的函数关系式是 ; (2)若商场计划每天的销售利润为2000元,则其单价应定为 元. 意图:通过阅读材料和表格,对生活中实际问题(销售问题)的考查,巩固反比例函数概念和性质、用待定系数法求函数表达式. 题源:改编自深圳专版《新课标同步单元练习》九上P114第3题. 答案:(1);(2)180. (1)由表中数据得: ,∴x与y之间的函数关系式为; (2)由题意得,, 解得,x=180.
5.龙岗某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为15 20℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分,则下列说法错误的是( ) A.k的值为240 B.当x=1时,大棚内的温度为15℃ C.恒温系统在这天保持大棚内温度20℃的时间有10小时 D.恒温系统在这天保持大棚内温度在15 20℃的时间有16小时 意图:通过图象,对大棚内温度y(℃)随时间x(小时)变化的函数关系的考察,巩固反比例函数概念和性质、确定实际问题中自变量的取值范围,并会求出函数值. 题源:改编自2022年重庆市巴南区期末试卷第8题. 答案:D 由图象可知,反比例函数的表达式为,当y=15时,.恒温系统在这天保持大棚内温度在15 20℃的时间为16-2=14小时,故D错误.
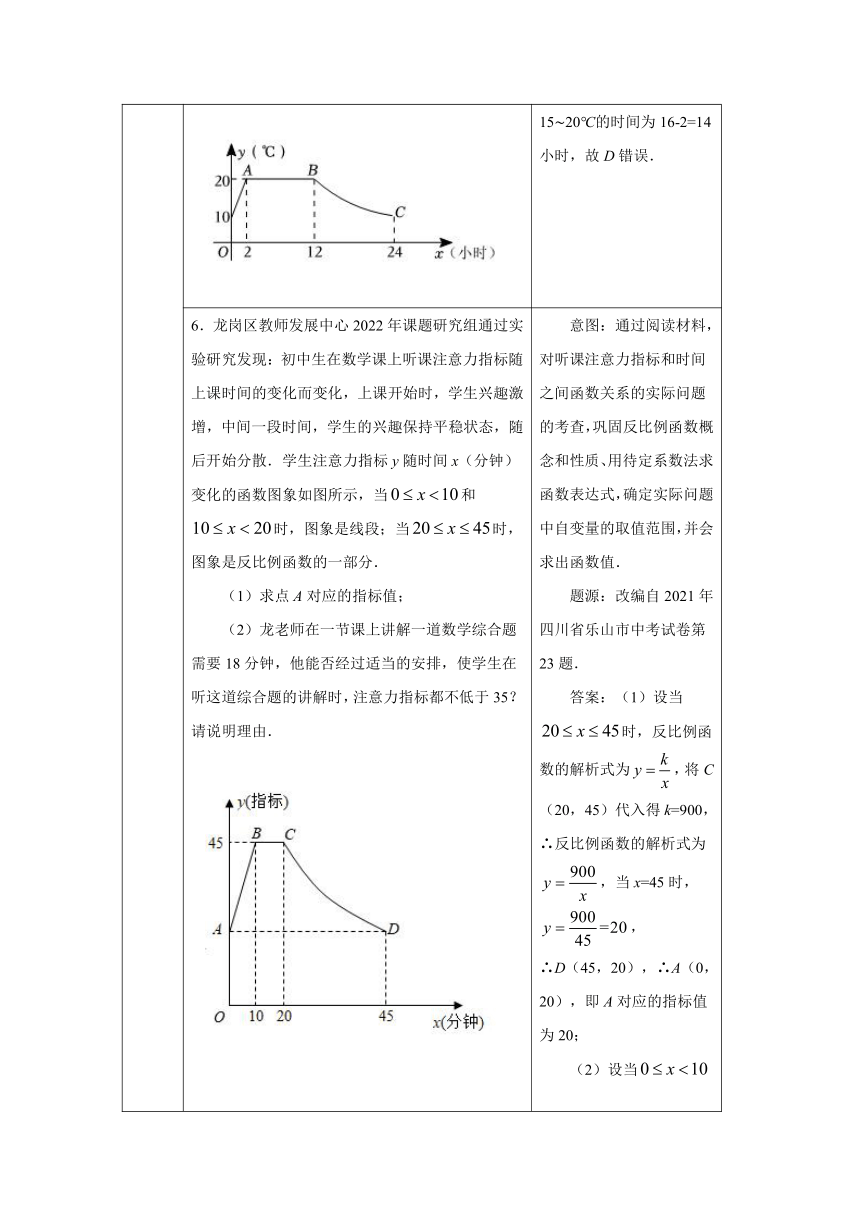
6.龙岗区教师发展中心2022年课题研究组通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当和时,图象是线段;当时,图象是反比例函数的一部分. (1)求点A对应的指标值; (2)龙老师在一节课上讲解一道数学综合题需要18分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于35?请说明理由. 意图:通过阅读材料,对听课注意力指标和时间之间函数关系的实际问题的考查,巩固反比例函数概念和性质、用待定系数法求函数表达式,确定实际问题中自变量的取值范围,并会求出函数值. 题源:改编自2021年四川省乐山市中考试卷第23题. 答案:(1)设当时,反比例函数的解析式为,将C(20,45)代入得k=900,∴反比例函数的解析式为,当x=45时,, ∴D(45,20),∴A(0,20),即A对应的指标值为20; (2)设当时,AB的解析式为,将A(0,20)、B(10,45)代入得:,解得 ,∴AB的解析式为,当y=35时,解得x=6. 由(1)得反比例函数的解析式为,当y=35时,解得, ∴时,注意力指标都不低于35,而 , ∴龙老师能经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于35.
课后作业 (拓展性作业) 7.杠杆原理在生活中应用广泛,我国早在春秋时期就有使用,相传商人范盐观农夫从井中取水受到启发,发明了称,其中就利用了杠杆原理. 杠杆原理为:阻力×阻力臂=动力×动力臂,如图1. 某数学兴趣小组利用这一原理制作了一个称量物体质量的简易“秤”(如图2).制作方法如下: 第一步:在一根匀质细木杆上标上均匀的刻度(单位长度1cm),确定支点O,并用细麻绳固定,在支点O左侧2cm的A处固定一个金属吊钩,作为秤钩; 第二步:取一个质量为0.5kg的金属物体作为秤砣. (1)图2中,把重物挂在秤钩上,秤砣挂在支点O右侧的B处,秤杆平衡,就能称得重物的质量.当重物的质量变化时,OB的长度随之变化.设重物的质量为x kg,OB的长为y cm.写出y关于x的函数解析式;若0<y<40,求x的取值范围. (2)调换秤砣与重物的位置,把秤砣挂在秤钩上,重物挂在支点O右侧的B处,使秤杆平衡,如图3.设重物的质量为x kg,OB的长为y cm,写出y关于x的函数解析式,完成下表,画出该函数的图象. x/kg…0.250.5124…y/cm……
意图:通过阅读材料,对杠杆原理中函数关系的实际问题的考查,巩固正比例函数和反比例函数概念和性质、用待定系数法求函数表达式,确定实际问题中自变量的取值范围,并会画出函数图象. 题源:改编自2022年山东省临沂市中考试卷第20题. 答案:(1)∵阻力×阻力臂=动力×动力臂, ∴重物重力×OA=秤砣重力×OB, ∴2x=0.5y, ∴y=4x, ∵4>0, ∴y随x的增大而增大, ∵当y=0时,x=0; 当y=40时,x=10, ∴0<x<10; (2)∵阻力×阻力臂=动力×动力臂, ∴秤砣×OA=重物×OB, ∴2×0.5=xy, ∴, 当x=0.25时,y=4; 当x=0.5时,y=2; 当x=1时,y=1; 当x=2时,y=0.5; 当x=4时,y=0.25; 故答案为:4;2;1;0.5;0.25; 作函数图象如图:
8.【背景】在探究电流和电阻关系的物理实验中,小龙同学用一固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R、RL之间关系为 ,通过实验得出如下数据: R/Ω…1a346…I/A…432.42b…
(1)a= ,b= ; (2)【探究】根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质. ①在平面直角坐标系中画出对应函数的图象; ②随着自变量x的不断增大,函数值y的变化趋势是 . (3)【拓展】结合(2)中函数图象分析,当时,的解集为 . 意图:通过阅读材料,对物理实验中函数关系的实际问题的考查,巩固反比例函数概念、图象和性质,画出函数图象并利用数形结合的思想解决问题. 题源:改编自2023年四川省达州市中考试卷第23题. 答案:(1)2,1.5; (2)①根据表格数据描点,在平面直角坐标系中画出对应函数的图象如下: ②由图象可知,随着自变量x的不断增大,函数值y的变化趋势是不断减小,故答案为:不断减小; (3)或..
预计完成时间 本课时课堂设计练习为2道题,课后作业分基础性作业(6道题)+拓展性作业(2道题) 课后作业中的基础性作业预计完成时间是20分钟.
作业评价方式 从知识获得、能力提升、学习态度、学习方法、价值观念培育等方面设计作业评价的内容、方式与工具.围绕课标,关注素养提升,瞄准作业目标,做到教、学、评一致. 水平问题解决水平4正确解决6道题水平3正确解决4道题水平2正确解决3道题水平1正确解决1道题
评价方式及标准评价指标等级ABC知识获得能力提升学习态度学习方法价值观念培育综合评价等级
作业类型 作业内容 设计意图、设计依据、 参考答案
课堂作业 1.随着新业态兴起和深圳市民出行习惯的改变,电动自行车已经成为当下重要的交通工具.已知电动自行车蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系().下列反映电流I与电阻R之间函数关系的图象大致是( ) (主要对应单元目标:910610) 意图:通过对生活中实际问题电流、电压、电阻函数关系的考察,巩固反比例函数的概念、图象和性质. 题源:改编自2023年湖北省荆州市中考试卷第4题. 答案:B ∵电流I与电阻R是反比例函数关系(),R、I均大于0, ∴反映电流I与电阻R之间函数关系的图象大致是B选项,故选:B.
2.龙岗燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2)与其深度d(单位:m)是反比例函数关系,它的图象如图所示. (1)写出这一函数的表达式; (2)当深度为10 m时,求储存室的容积V的值; (3)受地形条件限制,储存室的深度d需要满足,直接写出储存室的底面积S的取值范围. 意图:通过阅读材料,对天然气储存室的底面积和深度之间函数关系的实际问题的考查,巩固反比例函数概念和性质、用待定系数法求函数表达式,会求出函数值和确定实际问题中自变量的取值范围. 题源:改编自北师大版教材习题6.4第24题. 答案:(1)设反比例函数表达式为,把点(20,500)代入表达式得V=10000.∴反比例函数的表达式为 (2)当d=10时,,∴储存室的容积V的值为1000. (3)
课后作业 (基础性作业) 1.在日常生活中有许多现象应用了反比例函数,下列现象:①百米赛跑时,用时越短,成绩越好;②购买同一商品,买的越多,花钱越多;③从网上下载同一文件,网速越快,用时越少;④把游泳池放满水,水流越大,用时越短.其中符合反比例函数的现象有( ) A.1个 B.2个 C.3个 D.4个 意图:通过对生活中实际情境中函数关系的判断,巩固反比例函数的概念. 题源:自编题. 答案:C ②购买同一商品,买的越多,花钱越多是正比例关系,故本小题错误;
2.大运公园中常常能见到用鹅卵石铺成的凹凸不平的道路,人在上面行走时能够对脚底有一定的按摩作用.已知压力F(N)、压强P(Pa)与受力面积S(m2)之间有如下关系式:F=PS.当F为定值时,如图中大致表示压强P与受力面积S之间函数关系的是( ) 意图:通过对生活中实际问题中函数关系的判断,巩固反比例函数的图象. 题源:改编自2023年湖南省怀化市中考试卷第9题. 答案:D ∵压力F、压强P与受力面积S之间有如下关系式:F=PS. ∴当F为定值时,压强P与受力面积S之间函数关系是反比例函数, 故选:D.
3.已知电动自行车蓄电池的电压为定值,使用某蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则当电阻为6Ω时,电流为( ) A.3A B.4A C.6A D.8 A 意图:通过对生活中实际问题电流、电压、电阻函数关系的考察,巩固反比例函数的概念、图象和性质. 题源:改编自北师大版教材P158做一做. 答案:B 解:设,∵图象过(8,3),∴U=24,∴,当电阻为6Ω时,电流为:(A).
4.深圳中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该品牌运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示: 第1天第2天第3天第4天售价x/元150200250300销售量y/双40302420
(1)表中数据, x与y满足的函数关系式是 ; (2)若商场计划每天的销售利润为2000元,则其单价应定为 元. 意图:通过阅读材料和表格,对生活中实际问题(销售问题)的考查,巩固反比例函数概念和性质、用待定系数法求函数表达式. 题源:改编自深圳专版《新课标同步单元练习》九上P114第3题. 答案:(1);(2)180. (1)由表中数据得: ,∴x与y之间的函数关系式为; (2)由题意得,, 解得,x=180.
5.龙岗某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为15 20℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分,则下列说法错误的是( ) A.k的值为240 B.当x=1时,大棚内的温度为15℃ C.恒温系统在这天保持大棚内温度20℃的时间有10小时 D.恒温系统在这天保持大棚内温度在15 20℃的时间有16小时 意图:通过图象,对大棚内温度y(℃)随时间x(小时)变化的函数关系的考察,巩固反比例函数概念和性质、确定实际问题中自变量的取值范围,并会求出函数值. 题源:改编自2022年重庆市巴南区期末试卷第8题. 答案:D 由图象可知,反比例函数的表达式为,当y=15时,.恒温系统在这天保持大棚内温度在15 20℃的时间为16-2=14小时,故D错误.
6.龙岗区教师发展中心2022年课题研究组通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当和时,图象是线段;当时,图象是反比例函数的一部分. (1)求点A对应的指标值; (2)龙老师在一节课上讲解一道数学综合题需要18分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于35?请说明理由. 意图:通过阅读材料,对听课注意力指标和时间之间函数关系的实际问题的考查,巩固反比例函数概念和性质、用待定系数法求函数表达式,确定实际问题中自变量的取值范围,并会求出函数值. 题源:改编自2021年四川省乐山市中考试卷第23题. 答案:(1)设当时,反比例函数的解析式为,将C(20,45)代入得k=900,∴反比例函数的解析式为,当x=45时,, ∴D(45,20),∴A(0,20),即A对应的指标值为20; (2)设当时,AB的解析式为,将A(0,20)、B(10,45)代入得:,解得 ,∴AB的解析式为,当y=35时,解得x=6. 由(1)得反比例函数的解析式为,当y=35时,解得, ∴时,注意力指标都不低于35,而 , ∴龙老师能经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于35.
课后作业 (拓展性作业) 7.杠杆原理在生活中应用广泛,我国早在春秋时期就有使用,相传商人范盐观农夫从井中取水受到启发,发明了称,其中就利用了杠杆原理. 杠杆原理为:阻力×阻力臂=动力×动力臂,如图1. 某数学兴趣小组利用这一原理制作了一个称量物体质量的简易“秤”(如图2).制作方法如下: 第一步:在一根匀质细木杆上标上均匀的刻度(单位长度1cm),确定支点O,并用细麻绳固定,在支点O左侧2cm的A处固定一个金属吊钩,作为秤钩; 第二步:取一个质量为0.5kg的金属物体作为秤砣. (1)图2中,把重物挂在秤钩上,秤砣挂在支点O右侧的B处,秤杆平衡,就能称得重物的质量.当重物的质量变化时,OB的长度随之变化.设重物的质量为x kg,OB的长为y cm.写出y关于x的函数解析式;若0<y<40,求x的取值范围. (2)调换秤砣与重物的位置,把秤砣挂在秤钩上,重物挂在支点O右侧的B处,使秤杆平衡,如图3.设重物的质量为x kg,OB的长为y cm,写出y关于x的函数解析式,完成下表,画出该函数的图象. x/kg…0.250.5124…y/cm……
意图:通过阅读材料,对杠杆原理中函数关系的实际问题的考查,巩固正比例函数和反比例函数概念和性质、用待定系数法求函数表达式,确定实际问题中自变量的取值范围,并会画出函数图象. 题源:改编自2022年山东省临沂市中考试卷第20题. 答案:(1)∵阻力×阻力臂=动力×动力臂, ∴重物重力×OA=秤砣重力×OB, ∴2x=0.5y, ∴y=4x, ∵4>0, ∴y随x的增大而增大, ∵当y=0时,x=0; 当y=40时,x=10, ∴0<x<10; (2)∵阻力×阻力臂=动力×动力臂, ∴秤砣×OA=重物×OB, ∴2×0.5=xy, ∴, 当x=0.25时,y=4; 当x=0.5时,y=2; 当x=1时,y=1; 当x=2时,y=0.5; 当x=4时,y=0.25; 故答案为:4;2;1;0.5;0.25; 作函数图象如图:
8.【背景】在探究电流和电阻关系的物理实验中,小龙同学用一固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R、RL之间关系为 ,通过实验得出如下数据: R/Ω…1a346…I/A…432.42b…
(1)a= ,b= ; (2)【探究】根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质. ①在平面直角坐标系中画出对应函数的图象; ②随着自变量x的不断增大,函数值y的变化趋势是 . (3)【拓展】结合(2)中函数图象分析,当时,的解集为 . 意图:通过阅读材料,对物理实验中函数关系的实际问题的考查,巩固反比例函数概念、图象和性质,画出函数图象并利用数形结合的思想解决问题. 题源:改编自2023年四川省达州市中考试卷第23题. 答案:(1)2,1.5; (2)①根据表格数据描点,在平面直角坐标系中画出对应函数的图象如下: ②由图象可知,随着自变量x的不断增大,函数值y的变化趋势是不断减小,故答案为:不断减小; (3)或..
预计完成时间 本课时课堂设计练习为2道题,课后作业分基础性作业(6道题)+拓展性作业(2道题) 课后作业中的基础性作业预计完成时间是20分钟.
作业评价方式 从知识获得、能力提升、学习态度、学习方法、价值观念培育等方面设计作业评价的内容、方式与工具.围绕课标,关注素养提升,瞄准作业目标,做到教、学、评一致. 水平问题解决水平4正确解决6道题水平3正确解决4道题水平2正确解决3道题水平1正确解决1道题
评价方式及标准评价指标等级ABC知识获得能力提升学习态度学习方法价值观念培育综合评价等级
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
