7.1为什么要证明同步练习(无答案)2023-2024学年北师大版数学 八年级 上册
文档属性
| 名称 | 7.1为什么要证明同步练习(无答案)2023-2024学年北师大版数学 八年级 上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 112.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 09:03:54 | ||
图片预览


文档简介
7.1为什么要证明
一、选择题。
1.100人共有2000元人民币,其中任意10人的钱数的和不超过380元.那么一个人最多有( )元.
A.216 B.218 C.238 D.236
2.有三位同学对校队与市队足球赛进行估计,A说:校队至少进3个球,B说:校队进球数不到5个,C说:校队至少进1个球.比赛后,知道3个人中,只有1个人的估计是对的,你能知道,校队踢进球的个数是( )
A.4个 B.3个 C.1个 D.0个
3.下列说法正确的是( )
A.经验、观察或实验完全可以判断一个数学结论的正确与否
B.推理是科学家的事,与我们没有多大的关系
C.对于自然数n,n2+n+37一定是质数
D.有10个苹果,将它放进9个筐中,则至少有一个筐中的苹果不少于2个
4.骑自行车的速度是每小时15千米,骑摩托车的速度每小时40千米,则下列结论中你能肯定的是( )
A.从A地到B地,骑摩托车的人比骑自行车的人一定先到达
B.从A地到B地,骑自行车的人比骑摩托车的人后到达
C.从A地到B地,骑自行车和骑摩托车的不可能同时到达
D.从A地到B地,骑自行车的人有可能比骑摩托车的人先到达
5.下列几个命题中正确的个数为( )
①“掷一枚均匀骰子,朝上点数为负”为必然事件(骰子上各面点数依次为1,2,3,4,5,6);
②5名同学的语文成绩为90,92,92,98,103,则他们的平均分为95,众数为92;
③射击运动员甲、乙分别射击10次,算得甲击中环数的方差为4,乙击中环数的方差为16,则这一过程中乙较甲更稳定;
④某部门15名员工个人年创利润统计表如下,其中有一栏被污渍弄脏看不清数据,所以对于“该部门员工个人年创利润的中位数为5万元”的说法无法判断对错.
个人年创利润/万元 10 8 5 3
员工人数 1 3 4
A.1个 B.2个 C.3个 D.4个
6.小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多多少道( )
A.15 B.20 C.25 D.30
7.在一次400米比赛中,有如下的判断:甲说:丙第一,我第三;乙说:我第一,丁第四;丙说:丁第二,我第三.结果是每人的两句话中都只说对了一句,则可判断第一名是().
A.甲 B.乙 C.丙 D.丁
8.布鲁斯先生、他的妹妹、他的儿子,还有他的女儿都是网球选手.这四人中有以下情况:①最佳选手的孪生同胞与最差选手性别不同:②最佳选手与最差选手年龄相同.则这四人中最佳选手是( )
A.布鲁斯先生 B.布鲁斯先生的妹妹
C.布鲁斯先生的儿子 D.布鲁斯先生的女儿
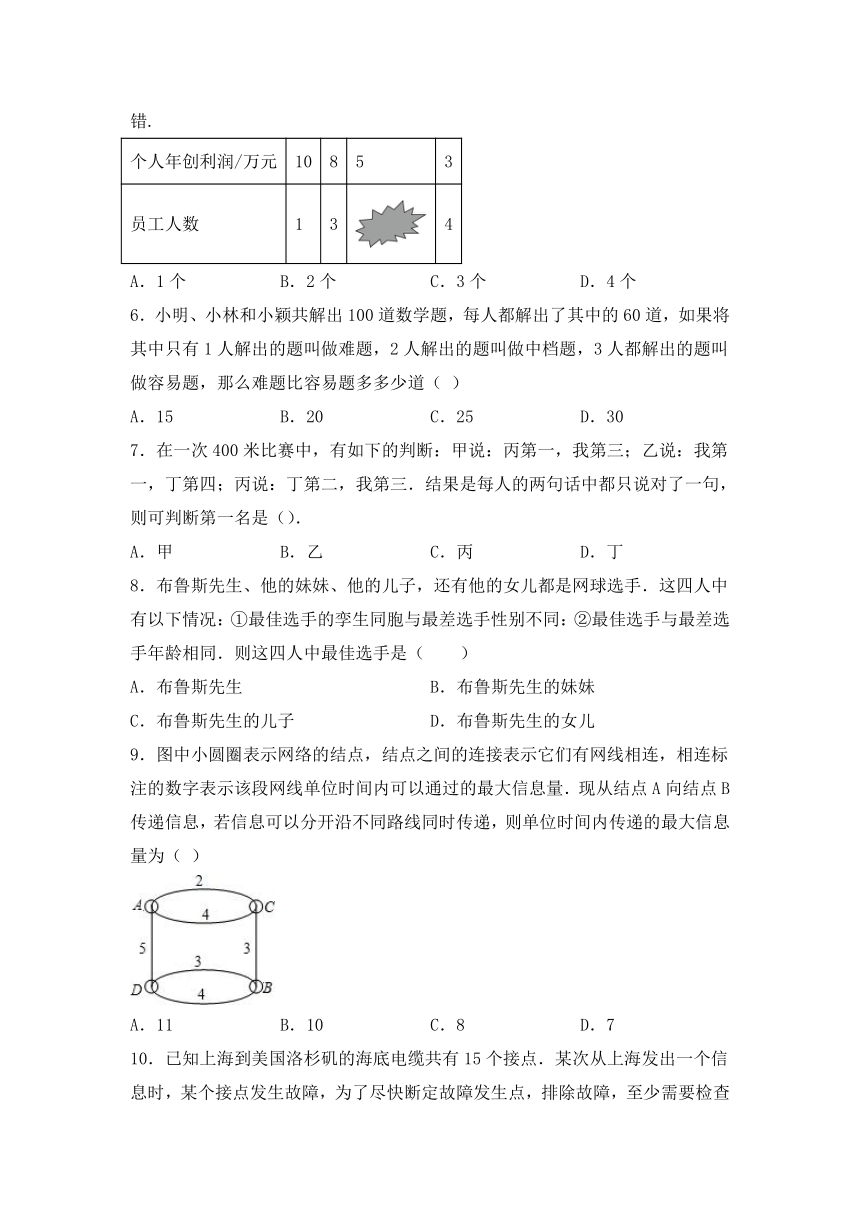
9.图中小圆圈表示网络的结点,结点之间的连接表示它们有网线相连,相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,若信息可以分开沿不同路线同时传递,则单位时间内传递的最大信息量为( )
A.11 B.10 C.8 D.7
10.已知上海到美国洛杉矶的海底电缆共有15个接点.某次从上海发出一个信息时,某个接点发生故障,为了尽快断定故障发生点,排除故障,至少需要检查的接点个数是( )
A.3 B.4 C.5 D.6
11.试说明“若,,,则”是真命题.以下是排乱的推理过程:
①因为(已知);
②因为,(已知);
③所以,(等式的性质);
④所以(等量代换);
⑤所以(等量代换).
正确的顺序是( )
A.①→③→②→⑤→④ B.②→③→⑤→①→④
C.②→③→①→⑤→④ D.②→⑤→①→③→④
12.边长为1的正方形OABC从如图所示的位置(点O对应数0,点A对应数-1)开始在数轴上顺时针滚动(无滑动).当正方形的某个顶点落在数2023在数轴上对应的点处时停止运动,此时落在数2023在数轴上对应点的这个顶点是( )
A.点A B.点B C.点C D.点O
13.如图所示,数轴上O,A两点的距离为8,一动点P从点A出发,按以下规律跳动:第1次跳动到AO的中点A1处,第2次从A1点跳动到A1O的中点A2处,第3次从A2点跳动到A2O的中点A3处,按照这样的规律继续跳动到点A4,A5,A6,…,An(n≥3,n是整数)处,问经过这样2023次跳动后的点与A1A的中点的距离是( )
A. B. C. D.
二、填空题。
1.有80朵花,按2红、3黄、4白的顺序排列,最后一朵是 花.
2.等腰三角形的底角必是 角(填“直”、“锐”或“钝”),为了说明你的结论正确,你可以从假设入手开始说明.
3.在乒乓球比赛中是没有平局的,都要分出胜负,甲、乙、丙三人进行乒乓球比赛,其中甲胜4局负2局,乙胜3局负3局,若丙负了3局,则丙胜了 局.
4.当时,代数式;当时, ;当时, ;当时, .因此,小明推断,不论取任何正整数,的值都是 ,这个推断是 的.(填“正确”或“错误”)
5.观察下列各式:(1);(2);(3);…,根据上述规律,则 .
6.为了说明“两个无理数的和是无理数”是错误的,可举两个无理数 和 ,显然它们的和是有理数.
7.金乡县某中学七年级共有四个班,每班各选5名同学组成一个代表队,这四支代表队(分别用A,B,C,D表示)进行数学知识应用竞赛,前三名将参加金乡县数学知识竞赛,甲,乙,丙三位同学预测的结果分别为:甲:C得亚军;D得季军;乙:D得冠军;A得亚军;丙:C得冠军;B得亚军.已知每人的预测都是半句正确,半句错误,则冠,亚,季,殿军分别为 .
三、解答题。
1.我们知道:,.试问:对于任意实数a与b,是否一定有结论?
2.观察下列各式,:×2=+2;×3=+3;×4=+4;×5=+5;……
想一想:什么样的两个数之积等于这两个数的和?设n表示正整数,用关于n的代数式表示这个规律为: × = + .你能说明吗?
3.三个同学在玩“我是大侦探”游戏,小张、小王、小李三人中有一个是卧底.小张说:“我就是卧底.”小王说:“我不是卧底.”小李说:“小张不是卧底.”他们三人中只有一人说的是真话,那么谁是真正的卧底?
4.卡钳是一个测量工件内槽宽的工具.如图,师傅通常把两根钢条,的中点连在一起,就可以做成一个简易卡钳.只要量得的长度,就可知工件的内径是否符合标准.请结合题意及图示,用符号语言写出已知和求证,并完成证明.
已知:
求证:
证明:
5.观察下列关于自然数的等式:
第1个等式: ;
第2个等式: ;
第3个等式: ;
第4个等式: ;
……
根据上述规律解决下列问题:
(1)写出第5个等式;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证你写的等式;
(3)在这n个等式中,等式右边结果能否是2021?请说明理由.
6.求证:三角形一边的两端点到这边的中线所在的直线的距离相等.
(解题要求:补全已知、求证,写出证明)
已知:如图,在中,是边上的中线,________.
求证:________.
证明:
一、选择题。
1.100人共有2000元人民币,其中任意10人的钱数的和不超过380元.那么一个人最多有( )元.
A.216 B.218 C.238 D.236
2.有三位同学对校队与市队足球赛进行估计,A说:校队至少进3个球,B说:校队进球数不到5个,C说:校队至少进1个球.比赛后,知道3个人中,只有1个人的估计是对的,你能知道,校队踢进球的个数是( )
A.4个 B.3个 C.1个 D.0个
3.下列说法正确的是( )
A.经验、观察或实验完全可以判断一个数学结论的正确与否
B.推理是科学家的事,与我们没有多大的关系
C.对于自然数n,n2+n+37一定是质数
D.有10个苹果,将它放进9个筐中,则至少有一个筐中的苹果不少于2个
4.骑自行车的速度是每小时15千米,骑摩托车的速度每小时40千米,则下列结论中你能肯定的是( )
A.从A地到B地,骑摩托车的人比骑自行车的人一定先到达
B.从A地到B地,骑自行车的人比骑摩托车的人后到达
C.从A地到B地,骑自行车和骑摩托车的不可能同时到达
D.从A地到B地,骑自行车的人有可能比骑摩托车的人先到达
5.下列几个命题中正确的个数为( )
①“掷一枚均匀骰子,朝上点数为负”为必然事件(骰子上各面点数依次为1,2,3,4,5,6);
②5名同学的语文成绩为90,92,92,98,103,则他们的平均分为95,众数为92;
③射击运动员甲、乙分别射击10次,算得甲击中环数的方差为4,乙击中环数的方差为16,则这一过程中乙较甲更稳定;
④某部门15名员工个人年创利润统计表如下,其中有一栏被污渍弄脏看不清数据,所以对于“该部门员工个人年创利润的中位数为5万元”的说法无法判断对错.
个人年创利润/万元 10 8 5 3
员工人数 1 3 4
A.1个 B.2个 C.3个 D.4个
6.小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多多少道( )
A.15 B.20 C.25 D.30
7.在一次400米比赛中,有如下的判断:甲说:丙第一,我第三;乙说:我第一,丁第四;丙说:丁第二,我第三.结果是每人的两句话中都只说对了一句,则可判断第一名是().
A.甲 B.乙 C.丙 D.丁
8.布鲁斯先生、他的妹妹、他的儿子,还有他的女儿都是网球选手.这四人中有以下情况:①最佳选手的孪生同胞与最差选手性别不同:②最佳选手与最差选手年龄相同.则这四人中最佳选手是( )
A.布鲁斯先生 B.布鲁斯先生的妹妹
C.布鲁斯先生的儿子 D.布鲁斯先生的女儿
9.图中小圆圈表示网络的结点,结点之间的连接表示它们有网线相连,相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,若信息可以分开沿不同路线同时传递,则单位时间内传递的最大信息量为( )
A.11 B.10 C.8 D.7
10.已知上海到美国洛杉矶的海底电缆共有15个接点.某次从上海发出一个信息时,某个接点发生故障,为了尽快断定故障发生点,排除故障,至少需要检查的接点个数是( )
A.3 B.4 C.5 D.6
11.试说明“若,,,则”是真命题.以下是排乱的推理过程:
①因为(已知);
②因为,(已知);
③所以,(等式的性质);
④所以(等量代换);
⑤所以(等量代换).
正确的顺序是( )
A.①→③→②→⑤→④ B.②→③→⑤→①→④
C.②→③→①→⑤→④ D.②→⑤→①→③→④
12.边长为1的正方形OABC从如图所示的位置(点O对应数0,点A对应数-1)开始在数轴上顺时针滚动(无滑动).当正方形的某个顶点落在数2023在数轴上对应的点处时停止运动,此时落在数2023在数轴上对应点的这个顶点是( )
A.点A B.点B C.点C D.点O
13.如图所示,数轴上O,A两点的距离为8,一动点P从点A出发,按以下规律跳动:第1次跳动到AO的中点A1处,第2次从A1点跳动到A1O的中点A2处,第3次从A2点跳动到A2O的中点A3处,按照这样的规律继续跳动到点A4,A5,A6,…,An(n≥3,n是整数)处,问经过这样2023次跳动后的点与A1A的中点的距离是( )
A. B. C. D.
二、填空题。
1.有80朵花,按2红、3黄、4白的顺序排列,最后一朵是 花.
2.等腰三角形的底角必是 角(填“直”、“锐”或“钝”),为了说明你的结论正确,你可以从假设入手开始说明.
3.在乒乓球比赛中是没有平局的,都要分出胜负,甲、乙、丙三人进行乒乓球比赛,其中甲胜4局负2局,乙胜3局负3局,若丙负了3局,则丙胜了 局.
4.当时,代数式;当时, ;当时, ;当时, .因此,小明推断,不论取任何正整数,的值都是 ,这个推断是 的.(填“正确”或“错误”)
5.观察下列各式:(1);(2);(3);…,根据上述规律,则 .
6.为了说明“两个无理数的和是无理数”是错误的,可举两个无理数 和 ,显然它们的和是有理数.
7.金乡县某中学七年级共有四个班,每班各选5名同学组成一个代表队,这四支代表队(分别用A,B,C,D表示)进行数学知识应用竞赛,前三名将参加金乡县数学知识竞赛,甲,乙,丙三位同学预测的结果分别为:甲:C得亚军;D得季军;乙:D得冠军;A得亚军;丙:C得冠军;B得亚军.已知每人的预测都是半句正确,半句错误,则冠,亚,季,殿军分别为 .
三、解答题。
1.我们知道:,.试问:对于任意实数a与b,是否一定有结论?
2.观察下列各式,:×2=+2;×3=+3;×4=+4;×5=+5;……
想一想:什么样的两个数之积等于这两个数的和?设n表示正整数,用关于n的代数式表示这个规律为: × = + .你能说明吗?
3.三个同学在玩“我是大侦探”游戏,小张、小王、小李三人中有一个是卧底.小张说:“我就是卧底.”小王说:“我不是卧底.”小李说:“小张不是卧底.”他们三人中只有一人说的是真话,那么谁是真正的卧底?
4.卡钳是一个测量工件内槽宽的工具.如图,师傅通常把两根钢条,的中点连在一起,就可以做成一个简易卡钳.只要量得的长度,就可知工件的内径是否符合标准.请结合题意及图示,用符号语言写出已知和求证,并完成证明.
已知:
求证:
证明:
5.观察下列关于自然数的等式:
第1个等式: ;
第2个等式: ;
第3个等式: ;
第4个等式: ;
……
根据上述规律解决下列问题:
(1)写出第5个等式;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证你写的等式;
(3)在这n个等式中,等式右边结果能否是2021?请说明理由.
6.求证:三角形一边的两端点到这边的中线所在的直线的距离相等.
(解题要求:补全已知、求证,写出证明)
已知:如图,在中,是边上的中线,________.
求证:________.
证明:
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
