2023~2024学年苏科版数学九年级上册 期末复习巩固提升练习(无答案)(圆周角问题专题巩固)
文档属性
| 名称 | 2023~2024学年苏科版数学九年级上册 期末复习巩固提升练习(无答案)(圆周角问题专题巩固) |  | |
| 格式 | docx | ||
| 文件大小 | 548.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 09:22:07 | ||
图片预览


文档简介
2023-2024学年苏科版数学九年级上册
期末复习巩固提升练习
(圆周角问题专题巩固)
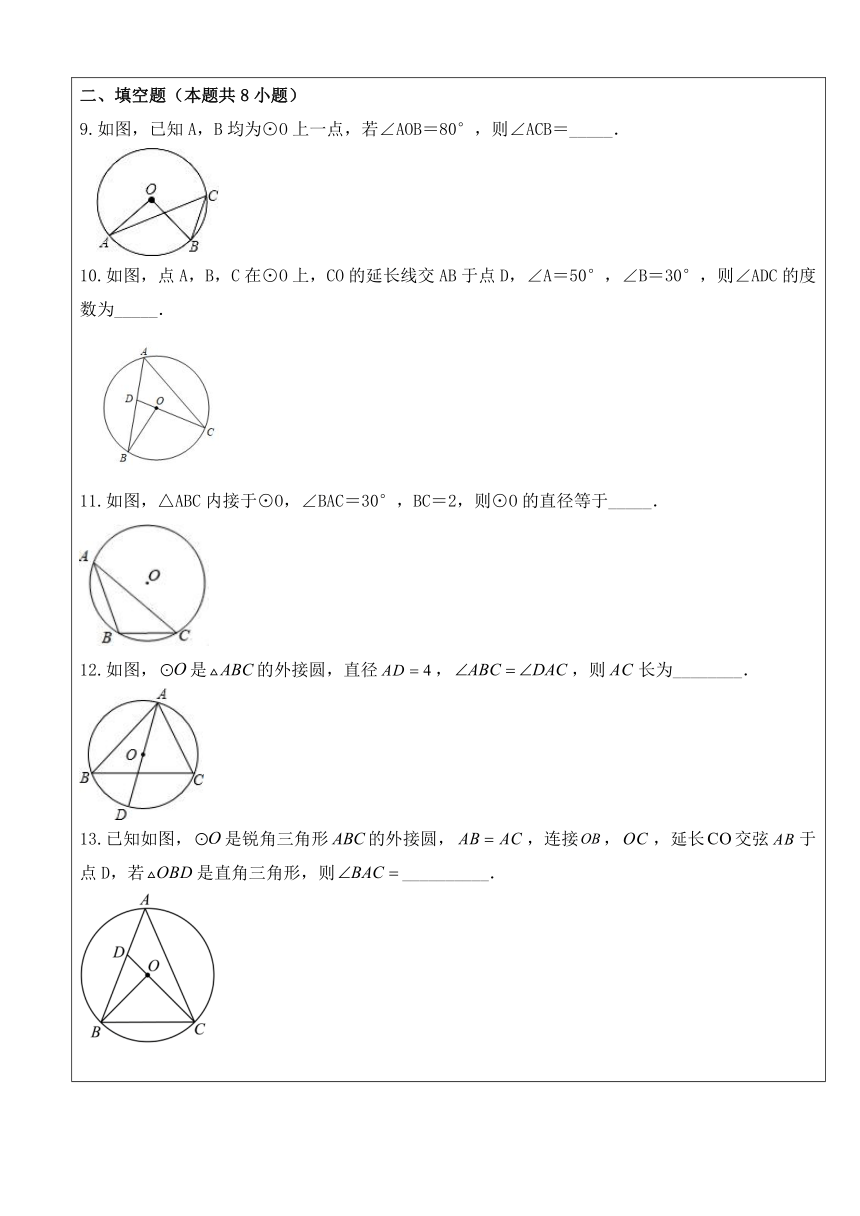
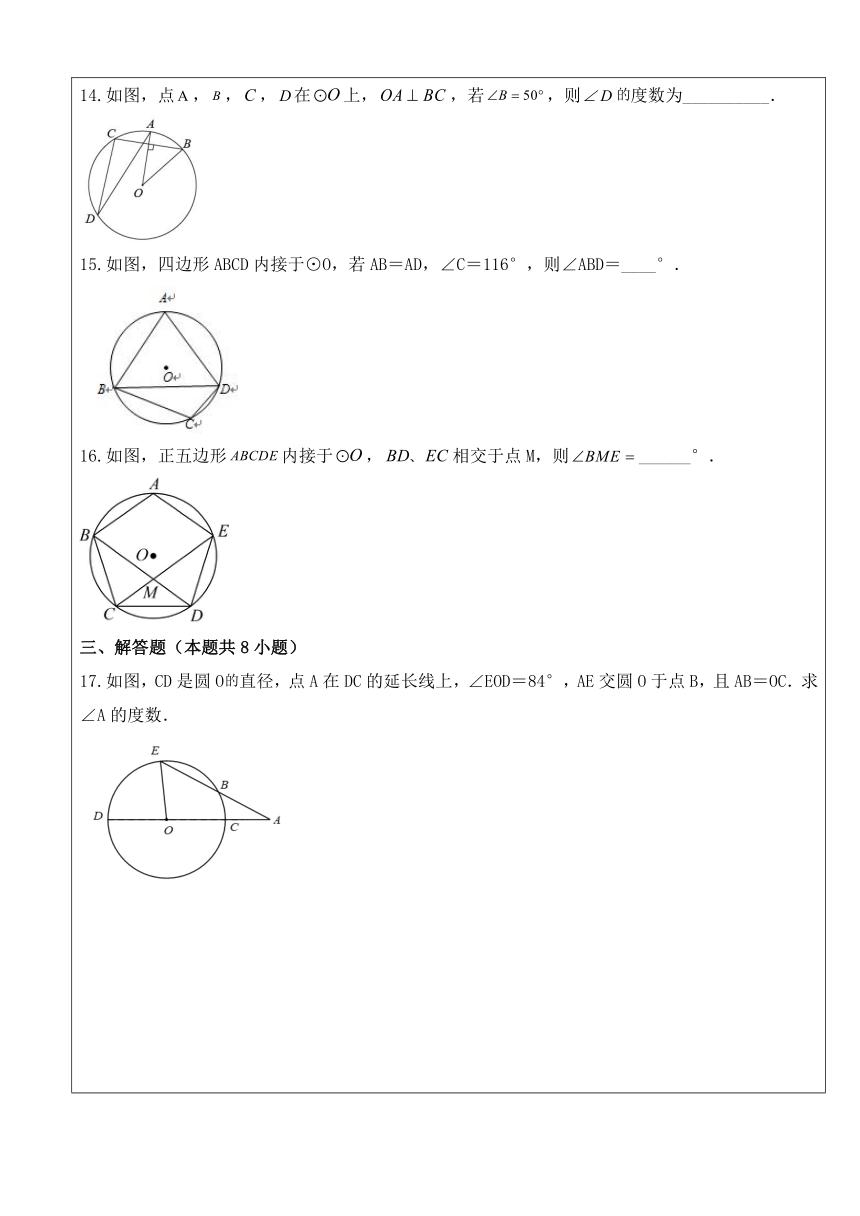
选择题(本题共8小题) 1.如图,AB是⊙O直径,点C在⊙O上,若∠A=40°,则∠B的度数为( ) A. 80° B. 60° C. 50° D. 40° 2.如图,点A、B、C都在⊙O上,若∠ABC=60°,则∠AOC的度数是( ) A. 100° B. 110° C. 120° D. 130° 3. 如图,点A、B、C是⊙O上的三点,若∠OBC=50°,则∠A的度数是( ) A. 40° B. 50° C. 80° D. 100° 4.如图,点A、B、C都在⊙O上,若∠AOC=140°,则∠B的度数是( ) A. 70° B. 80° C. 110° D. 140° 5.已知:如图, ⊙O的两条弦AE、BC相交于点D,连接AC、BE,若∠ACB=50°,则下列结论中正确的是( ) A. ∠AOB=50° B. ∠ADB=50° C. ∠AEB=30° D. ∠AEB=50° 6.如图,五边形是的内接正五边形,则正五边形中心角的度数是( ) A. B. C. D. 7.如图,是的直径,C、D是上的两点.若,则的度数为( ) A. 20° B. 40° C. 50° D. 70° 8.如图,是等边的外接圆,点是弧上一动点(不与,重合),下列结论:①;②;③当最长时,;④,其中一定正确的结论有( ) A.1个 B.2个 C.3个 D.4个 填空题(本题共8小题) 9.如图,已知A,B均为⊙O上一点,若∠AOB=80°,则∠ACB=_____. 10.如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为_____. 11.如图,△ABC内接于⊙O,∠BAC=30°,BC=2,则⊙O的直径等于_____. 12.如图,是的外接圆,直径,,则长为________. 13.已知如图,是锐角三角形的外接圆,,连接,,延长交弦于点D,若是直角三角形,则__________. 14.如图,点,,,在上,,若,则度数为__________. 15.如图,四边形ABCD内接于⊙O,若AB=AD,∠C=116°,则∠ABD=____°. 16.如图,正五边形内接于,相交于点M,则______°. 解答题(本题共8小题) 17.如图,CD是圆O直径,点A在DC的延长线上,∠EOD=84°,AE交圆O于点B,且AB=OC.求∠A的度数. 18.如图,四边形ABDC内接于⊙O,∠BAC=60°,AD平分∠BAC交⊙O于点D,连接OB,OC,BD,CD. (1)求证:四边形OBDC是菱形; (2)若∠ABO=15°,OB=2,求弦AC长. 19.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC (1)若∠CBD=39°,求∠BAD的度数 (2)求证:∠1=∠2 20.如图,AB是的一条弦,,垂足为C,交于点D,点E在上. (1)若∠AOD=50°,求的度数; (2)若,,求半径长. 21.如图,A,P,B,C是上的四个点,. (1)求∠ACB的度数; (2)若,求的长. 22.如图①,在中,,是外接圆上一点,连接,过点作,交的延长线于点,交于点. (1)求证:四边形是平行四边形; (2)如图②,若为直径,,,求的长. 23.已知:如图,AB是⊙O的直径,弦CD⊥AB于点E,连结CG,DG (1)若∠A=25°,求弧CD的度数; (2)求证:∠DGC=2∠BAC; (3)若⊙O的半径为5,BE=2,求弦AC的长. 24. (1)如图①,内接于,,点D在上. 求证:. 小明和小红在解决该问题时,有两种不同的添加辅助线的方式: 小明的作法 在上截取,连接……小红作法 延长至点,使得,连接……
请选择其中一种作法,完成证明: (2)如图②,内接于,BC是的直径,,点D在上.求证:. (3)如图③,内接于,BC是的直径,,点D在上.则,,之间的数量关系是______.
期末复习巩固提升练习
(圆周角问题专题巩固)
选择题(本题共8小题) 1.如图,AB是⊙O直径,点C在⊙O上,若∠A=40°,则∠B的度数为( ) A. 80° B. 60° C. 50° D. 40° 2.如图,点A、B、C都在⊙O上,若∠ABC=60°,则∠AOC的度数是( ) A. 100° B. 110° C. 120° D. 130° 3. 如图,点A、B、C是⊙O上的三点,若∠OBC=50°,则∠A的度数是( ) A. 40° B. 50° C. 80° D. 100° 4.如图,点A、B、C都在⊙O上,若∠AOC=140°,则∠B的度数是( ) A. 70° B. 80° C. 110° D. 140° 5.已知:如图, ⊙O的两条弦AE、BC相交于点D,连接AC、BE,若∠ACB=50°,则下列结论中正确的是( ) A. ∠AOB=50° B. ∠ADB=50° C. ∠AEB=30° D. ∠AEB=50° 6.如图,五边形是的内接正五边形,则正五边形中心角的度数是( ) A. B. C. D. 7.如图,是的直径,C、D是上的两点.若,则的度数为( ) A. 20° B. 40° C. 50° D. 70° 8.如图,是等边的外接圆,点是弧上一动点(不与,重合),下列结论:①;②;③当最长时,;④,其中一定正确的结论有( ) A.1个 B.2个 C.3个 D.4个 填空题(本题共8小题) 9.如图,已知A,B均为⊙O上一点,若∠AOB=80°,则∠ACB=_____. 10.如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为_____. 11.如图,△ABC内接于⊙O,∠BAC=30°,BC=2,则⊙O的直径等于_____. 12.如图,是的外接圆,直径,,则长为________. 13.已知如图,是锐角三角形的外接圆,,连接,,延长交弦于点D,若是直角三角形,则__________. 14.如图,点,,,在上,,若,则度数为__________. 15.如图,四边形ABCD内接于⊙O,若AB=AD,∠C=116°,则∠ABD=____°. 16.如图,正五边形内接于,相交于点M,则______°. 解答题(本题共8小题) 17.如图,CD是圆O直径,点A在DC的延长线上,∠EOD=84°,AE交圆O于点B,且AB=OC.求∠A的度数. 18.如图,四边形ABDC内接于⊙O,∠BAC=60°,AD平分∠BAC交⊙O于点D,连接OB,OC,BD,CD. (1)求证:四边形OBDC是菱形; (2)若∠ABO=15°,OB=2,求弦AC长. 19.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC (1)若∠CBD=39°,求∠BAD的度数 (2)求证:∠1=∠2 20.如图,AB是的一条弦,,垂足为C,交于点D,点E在上. (1)若∠AOD=50°,求的度数; (2)若,,求半径长. 21.如图,A,P,B,C是上的四个点,. (1)求∠ACB的度数; (2)若,求的长. 22.如图①,在中,,是外接圆上一点,连接,过点作,交的延长线于点,交于点. (1)求证:四边形是平行四边形; (2)如图②,若为直径,,,求的长. 23.已知:如图,AB是⊙O的直径,弦CD⊥AB于点E,连结CG,DG (1)若∠A=25°,求弧CD的度数; (2)求证:∠DGC=2∠BAC; (3)若⊙O的半径为5,BE=2,求弦AC的长. 24. (1)如图①,内接于,,点D在上. 求证:. 小明和小红在解决该问题时,有两种不同的添加辅助线的方式: 小明的作法 在上截取,连接……小红作法 延长至点,使得,连接……
请选择其中一种作法,完成证明: (2)如图②,内接于,BC是的直径,,点D在上.求证:. (3)如图③,内接于,BC是的直径,,点D在上.则,,之间的数量关系是______.
同课章节目录
