第3章图形的相似单元达标测试卷(含解析)2023-2024学年湘教版九年级数学上册
文档属性
| 名称 | 第3章图形的相似单元达标测试卷(含解析)2023-2024学年湘教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 413.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 11:10:31 | ||
图片预览



文档简介
湘教版九年级数学上册第3章图形的相似单元达标测试卷
一、单选题
1.如图,在△ABC中,如果DE与BC不平行,那么下列条件中,不能判断△ADE∽△ACB的是( )
A.∠ADE=∠C B.∠AED=∠B C. D.
2.若,则a=( )
A. B.1 C.2 D.3
3.下列各组图形中,一定是相似图形的是( )
A.两个等腰梯形 B.两个矩形
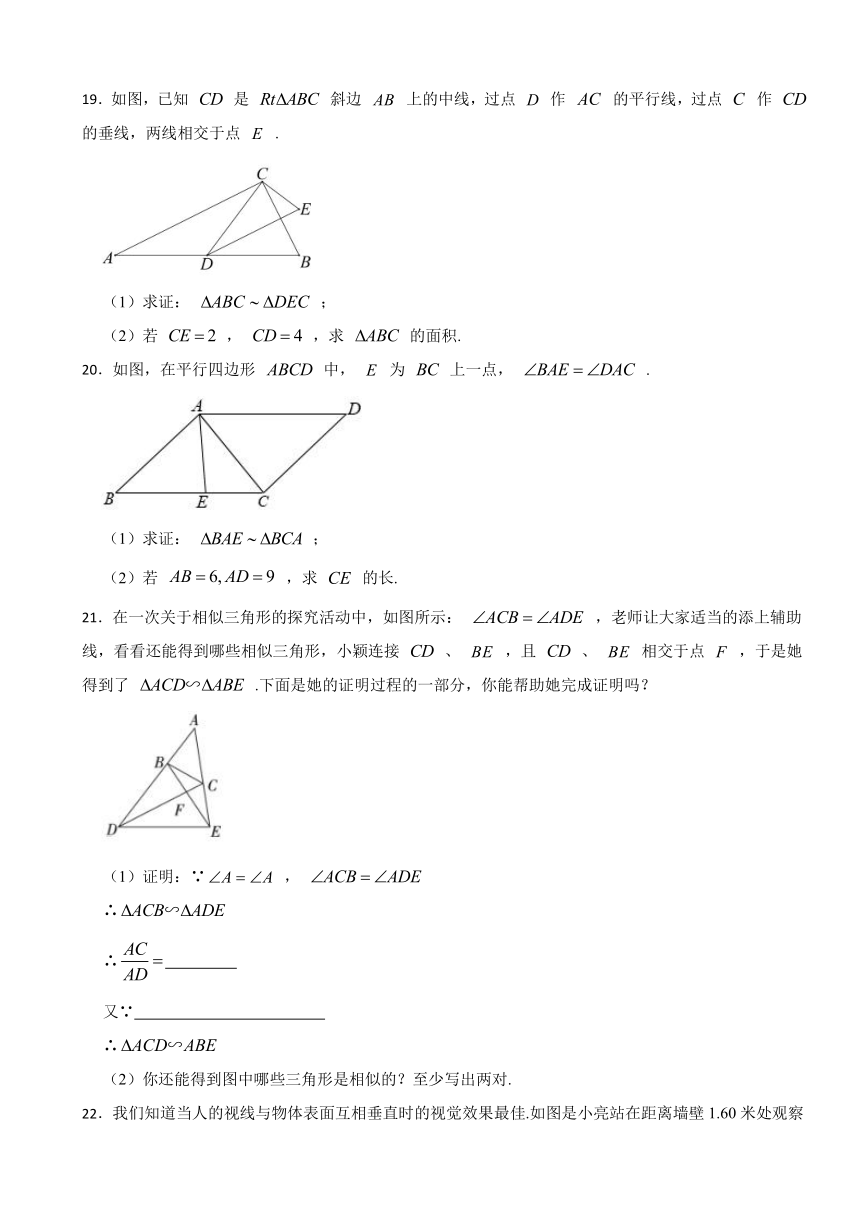
C.两个直角三角形 D.两个等边三角形
4.已知两个相似三角形的周长比为,若较大三角形的面积等于,则较小三角形的面积等于( )
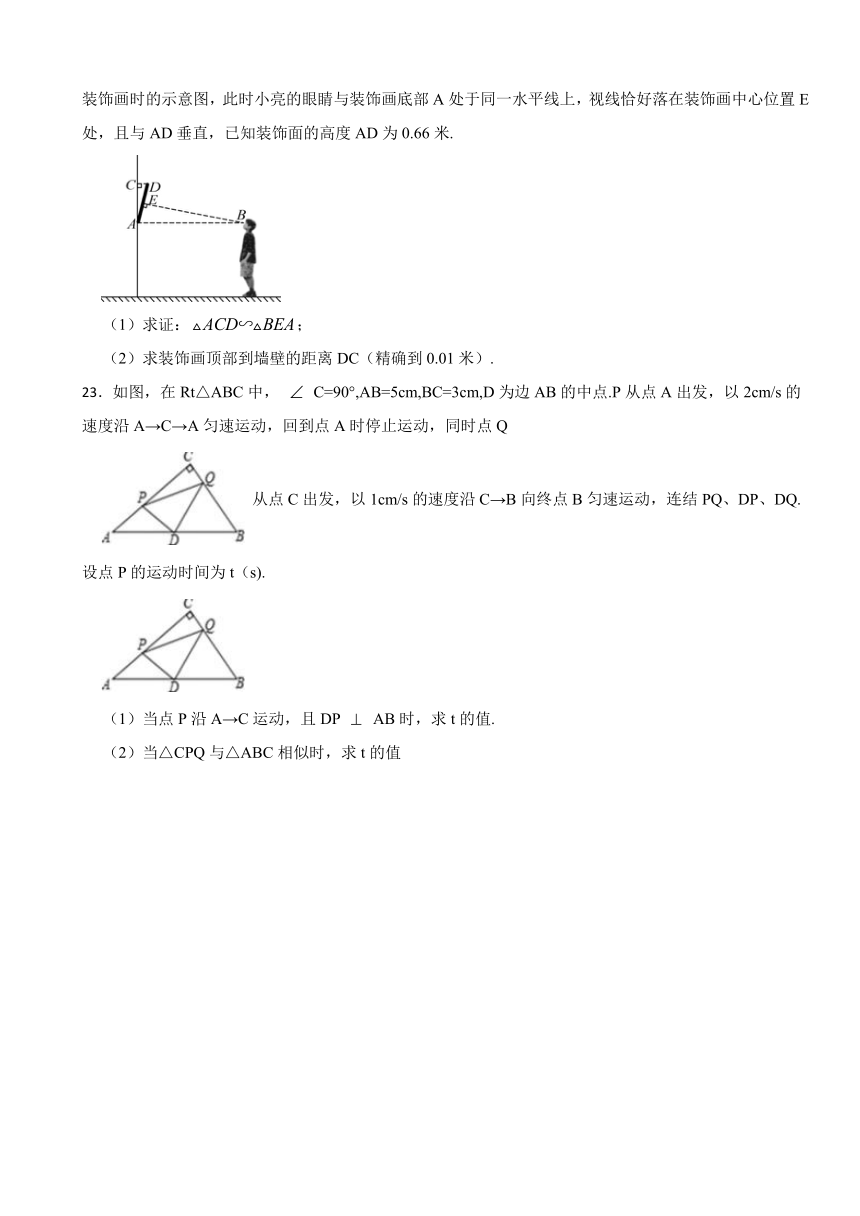
A. B. C. D.
5.如图,在 ABCD中,E是AB的中点 ,EC交BD于点F,那么SΔBEF:SΔBCF=( )
A.1:6 B.1:4 C.1:3 D.1:2
6.若△ABC∽△ADE,若AB=9,AC=6,AD=3,则EC的长是( )
A.2 B.3 C.4 D.5
7.两个相似多边形的面积比是9:16,其中较小多边形周长为36cm,则较大多边形周长为( )
A.48cm B.54cm C.56cm D.64cm
8.如图,已知四边形ABCD中,E、F分别为AB、CD 上的两点,且AD∥BC∥EF,AB=4BE,则DF与FC的关系是( )
A.DF=4FC B.DF=3FC C.DF= FC D.DF=2FC
9.在小孔成像问题中,如图所示,若为O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
A. B. C.2倍 D.3倍
10.如图,在正方形ABCD中,H是对角线BD的中点,延长DC至E,使得DE=DB,连接BE,作DF⊥BE交BC于点G,交BE于点F,连接CH、FH,下列结论:(1)HC=HF;(2)DG=2EF;(3)BE·DF=2CD2;(4)S△BDE=4S△DFH;(5)HF∥DE,正确的个数是( )
A.5 B.4 C.3 D.2
二、填空题
11.如图,若点P是AB的黄金分割点,则线段AP,PB,AB满足关系式 ,即AP是 与 的比例中项.
12.如图,Rt△ABC的边BC在x轴上,点D为斜边AB的中点,AC=3,BC=4,若反比例函数y= 的图象过点A、D,则k的值为 .
13.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长
14.综合实践课上,小慧用两张如图①所示的直角三角形纸片:∠A=90°,AD=2cm,AB=3cm,斜边重合拼成四边形,接着在CB,CD上取点E,F,连AE,BF,使AE⊥BF.
(1)若拼成的四边形如图②所示,则的值为 ;
(2)若拼成的四边形如图③所示,则的值为 .
三、解答题
15.即则称A为a,b的等差中项.如果按一定次序排列的三个数a,G,b满足即=ab(a,b同号),则称G为a,b的等比中项.根据前面给出的概念,求和的等差中项和等比中项.
16.如图,矩形ABCD中,点E为AD上一点,∠BEC=90°,AB=2,DE=1,求BC的长.
17.已知:平行四边形ABCD,E是BA延长线上一点,CE与AD、BD交于G、F.
求证:CF2=GF EF.
18.要做两个形状相同的三角形框架,其中一个三角形的三边长分别为4,5,6,另一个三角形的一边长为2,怎样选料可使这两个三角形相似?请说明理由.
四、综合题
19.如图,已知 是 斜边 上的中线,过点 作 的平行线,过点 作 的垂线,两线相交于点 .
(1)求证: ;
(2)若 , ,求 的面积.
20.如图,在平行四边形 中, 为 上一点, .
(1)求证: ;
(2)若 ,求 的长.
21.在一次关于相似三角形的探究活动中,如图所示: ,老师让大家适当的添上辅助线,看看还能得到哪些相似三角形,小颖连接 、 ,且 、 相交于点 ,于是她得到了 .下面是她的证明过程的一部分,你能帮助她完成证明吗?
(1)证明:∵ ,
∴
∴
又∵
∴
(2)你还能得到图中哪些三角形是相似的?至少写出两对.
22.我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小亮站在距离墙壁1.60米处观察装饰画时的示意图,此时小亮的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直,已知装饰面的高度AD为0.66米.
(1)求证:;
(2)求装饰画顶部到墙壁的距离DC(精确到0.01米).
23.如图,在Rt△ABC中, C=90°,AB=5cm,BC=3cm,D为边AB的中点.P从点A出发,以2cm/s的速度沿A→C→A匀速运动,回到点A时停止运动,同时点Q
从点C出发,以1cm/s的速度沿C→B向终点B匀速运动,连结PQ、DP、DQ.设点P的运动时间为t(s).
(1)当点P沿A→C运动,且DP AB时,求t的值.
(2)当△CPQ与△ABC相似时,求t的值
答案解析部分
1.【答案】D
【解析】【解答】∵∠DAE=∠CAB,
∴当∠AED=∠B或∠ADE=∠C时,△ABC∽△AED;
当 时,△ABC∽△AED.
故答案为:D.
【分析】因为∠A是公共角,所以由∠ADE=∠C(或∠AED=∠B)都可以根据有两个角对应相等的两个三角形相似可得△ABC∽△AED;当时,根据有两边的比相等,且它们的夹角也相等的两个三角形相似可得△ABC∽△AED;当时,不能判断两个三角形相似。
2.【答案】D
【解析】【解答】解:∵ ,
∴3(a-1)=2a,
∴a=3.
故答案为:D.
【分析】根据两内项之积等于两外项之积变为等积式,再去括号、移项、合并同类项即可得出a的值.
3.【答案】D
【解析】【解答】解:A:等腰梯形不一定是相似,不符合题意;
B:矩形不一定相似,不符合题意;
C:直角三角形不一定相似,不符合题意;
D:等边三角形一定相似,符合题意.
故答案为:D
【分析】根据相似图形的定义即可求出答案.
4.【答案】A
【解析】【解答】解:设较小三角形的面积等于,
由题意得:,
解得,
即较小三角形的面积等于,
故答案为:A.
【分析】根据相似三角形的面积比等于相似比的平方即可解答.
5.【答案】D
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴BECD,
∴∠BEC=∠DCF,∠EBF=∠CDF,
∴△EBF∽△CDF,
∴,
△BEF和△BCF分别选择EF、CF为底,则高相同,
∴,
故答案为:D.
【分析】先证明△EBF∽△CDF,可得,再利用等高的三角形的面积关系可得。
6.【答案】C
【解析】【解答】解:∵△ABC∽△ADE,
∴ ,
∵AB=9,AC=6,AD=3,
∴AE=2,
即EC=AC-AE=6-2=4;
故答案为:C.
【分析】利用相似三角形的性质得,对应边的比相等,求出AE的长,EC=AC-AE,即可计算DE的长;
7.【答案】A
【解析】【分析】根据相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方计算即可.
【解答】两个相似多边形的面积比是9:16,
面积比是周长比的平方,
则大多边形与小多边形的相似比是4:3.
相似多边形周长的比等于相似比,
因而设大多边形的周长为xcm,
则有=,
解得:x=48.
大多边形的周长为48cm.
故答案为A.
【点评】本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方
8.【答案】B
【解析】【解答】解:∵ AD∥BC∥EF,
∴,
又∵AB=4BE,
∴DC=4CF,
又∵DC=DF+FC,
∴DF=3FC。
故答案为:B.
【分析】根据平行线分线段成比例定理可得,,结合AB=4BE,可知DC=4FC,据此即可判断。
9.【答案】A
【解析】【解答】解:如图,作OE⊥AB于E,EO的延长线交CD于F.
∵AB∥CD,
∴FO⊥CD,△AOB∽△DOC,
∴ = = = (相似三角形的对应高的比等于相似比),
∴CD= AB,
故选A.
【分析】如图,作OE⊥AB于E,EO的延长线交CD于F.由△AOB∽△DOC,推出 = = = (相似三角形的对应高的比等于相似比),由此即可解决问题.
10.【答案】B
【解析】【解答】解:∵BD=DE,DF⊥BE,
∴EF=BF,
∵H是正方形ABCD对角线BD的中点,
∴CH=DH=BH= BD,
∴HF是△BDE的中位线,
∴HF= DE= BD=CH,HF//DE,故①⑤正确,
∵∠CBE+∠E=90°,∠FDE+∠E=90°,
∴∠CBE=∠FDE,
又∵CD=BC,∠DCG=∠BCE=90°,
∴△BCE≌△DCG,
∴DG=BE,
∵BE=2EF,
∴DG=2EF,故②正确,
∵∠CBE=∠FDE,∠E=∠E,
∴△BCE∽△DFE,
∴ ,即BE·DF=DE·BC,
∵BD2=CD2+BC2=2CD2
∴DE2=2CD2,
∴DE·BC≠2CD2,
∴BE·DF≠2CD2,故③错误,
∵DH= BD,
∴S△DFH= S△DFB,
∵BF= BE,
∴S△DFB= S△BDE,
∴S△DFH= S△BDE,即S△BDE=4S△DFH,故④正确,
综上所述:正确的结论有①②④⑤,共4个,
故答案为:B.
【分析】由等腰三角形“三线合一”的性质可得EF=BF,根据H是正方形对角线BD的中点可得CH=DH=BH,即可证明HF是△BDE的中位线,可得HF= DE,HF//DE;由BD=DE即可得HC=HF;利用直角三角形两锐角互余的关系可得∠CBE=∠CDG,利用ASA可证明△BCE≌△DCG,可得DG=BE,可判定DG=2EF,由正方形的性质可得BD2=2CD2,根据∠CBE=∠CDG,∠E是公共角可证明△BCE∽△DFE,即可得 ,即BE·DF=DE·BC,可对③进行判定,根据等底等高的三角形面积相等可对④进行判定,综上即可得答案.
11.【答案】;PB;AB
【解析】【解答】解:若点P是AB的黄金分割点,则线段AP,PB,AB满足关系式 ,即AP是PB与 AB的比例中项.
故答案为: ,PB、AB.
【分析】根据黄金分割的定义进行填空即可.
12.【答案】6
【解析】【解答】解:作DE⊥x轴于E,如图:
∵∠ACB=90°,
∴DE∥AC,
∴ ,
∴ ,
∵点D为斜边AB的中点,
∴E是BC的中点,即 ,
∴DE= AC= ,
设A(m,3),则D(m+2, ),
∵反比例函数 的图象过点A、D,
∴k=3m=(m+2)× ,
∴m=2,
∴k=3m=6,
故答案为:6.
【分析】作DE⊥x轴于E,利用DE∥AC,可证得△BDE∽△BAC,利用相似三角形的对应边成比例得出 ,利用线段中点的定义求出BE,DE的长;设A(m,3),则D(m+2, ),利用反比例函数图象上的点的坐标特点建立关于m的方程,解方程求出m的值,然后求出k的值.
13.【答案】AD=4
【解析】【解答】
解:∵∠C=∠ADE=90°,∠A=∠A,
∴△ADE∽△ACB,
∴
∴ ,
∴AD=4.
【分析】先证明△ADE∽△ACB,可得,再将数据代入计算即可。
14.【答案】(1)
(2)
【解析】【解答】解:(1)∵, ,
∴.
∵,
∴,
∴.
故答案为: ;
(2)如图,连接AC、BD,且交于点H,设AE、BD交于点G.
由题意四边形ABCD是由两个完全一样的三角形拼成,即A点和C点关于BD对称,
∴, .
∵在 中, ,
∴.
∵,
∴,即
解得: ,
∴.
∵, ,
∴.
∵, , ,
∴,
即在 和 中, ,
∴,
∴.
故答案为: , .
【分析】(1)证明 ,利用相似三角形的性质即可求解;
(2)连接AC、BD,且交于点H,设AE、BD交于点G,先求出BD、AH、AC,再证 ,可得 ,继而得解.
15.【答案】解:和的等差中项为,
和的等比中项为.
【解析】【分析】若a,b,c三个数按这个顺序排列成等差数列,那么b叫a,c的等差中项,且a, b, c满足b-a=c-b;一般地,如果一个数列的首项不为0,且从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列;根据等差数列和等比数列定义计算即可求解.
16.【答案】解:∵四边形ABCD为矩形,
∴∠D=90°,DC=AB=2,AD∥BC,
∴∠BEC=∠D,
∵DE=1,
∴EC2=CD2+DE2=5,
∵AD∥BC,
∴∠DEC=∠ECB,
∴△DEC∽△ECB,
∴ ,
∴ .
【解析】【分析】先利用矩形性质得出∠D=90°,DC=AB=2,AD∥BC,然后进一步利用勾股定理得出EC2=CD2+DE2=5,最后证明△DEC∽△ECB,利用相似三角形性质进一步求解即可.
17.【答案】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴=,=,
∴=,
即CF2=GF EF.
【解析】【分析】根据平行四边形的性质得AD∥BC,AB∥CD,再根据平行线分线段成比例定理得=,=,利用等量代换得到=,然后根据比例的性质即可得到结论.
18.【答案】解:设另一个三角形的两条边为x,y,
∵两个三角形是相似三角形,
则,
解得:,;
则,
解得:,;
则,
解得:,;
综上,当三角形的三边为:2,,;或2,,或2,,时,两个三角形是相似三角形.
【解析】【分析】根据题意设另一个三角形的两条边为x,y,结合相似三角形的对应边成比例即可列出相似比的等式,求解即可得出答案.
19.【答案】(1)证明:∵ 为 斜边上的中线,
∴ ,
∴ ,
∵ ,
∴ ,
又∵ ,
∴
(2)解:在 中, , ,
∴ , ,
∵ 为 斜边上的中线,
∴ ,
∵ ,
∴ ,即 ,
∴ .
【解析】【分析】(1)由直角三角形斜边上的中线等于斜边的一半可得CD=AD=AB,根据等边对等角可得∠A=∠ACD,再由平行线的性质可得∠CDE=∠ACD=∠A,于是根据有两对角对应相等的两个三角形相似可得△ABC∽△DEC;
(2)在直角三角形DCE中,用勾股定理可求得DE的长,根据S△DEC=CD.CE可求得三角形的面积;由直角三角形斜边上的中线等于斜边的一半可得AB=2CD,由(1)知,△ABC∽△DEC,根据相似三角形的面积的比等于相似比的平方可得,把AB、DE、S△DEC的值的代入计算即可求解。
20.【答案】(1)证明:∵四边形 是平行四边形,
∴ ,
∴ ,
∵ ,
∴
又∵ ,
∴
(2)解:∵四边形 是平行四边形
∴ ,
由(1)知: ,
∴ ,
∴ ,
∴ ,
∴
【解析】【分析】(1)根据平行四边形的对边平行得出AD∥BC,根据平行线的性质可得 ,从而可得 ,又 ,根据有两组角对应相等的两个三角形相似可得出结论;
(2)根据相似三角形的对应边成比例建立方程,求解即可.
21.【答案】(1);∠A=∠A,
(2)解:△DFB∽△EFC,△BFC∽△DFE.
理由:∵△ACD∽△ABE,
∴∠BDF=∠FEC,
∵∠DFB=∠EFC,
∴△DFB∽△EFC,
∴ ,
∴ ,
∵∠BFC=∠EFD,
∴△BFC∽△DFE
【解析】【解答】解:证明:∵∠A=∠A,∠ACB=∠ADE
∴△ACB∽△ADE
∴
又∵∠A=∠A,
∴△ACD∽△ABE
【分析】(1)根据两边成比例夹角相等两个三角形相似证明即可;(2)相似三角形还有:△DFB∽△EFC,△BFC∽△DFE.
22.【答案】(1)解:由题意可知∠DCA=∠BEA=∠CAB=90°
∵∠CAD+∠BAE=∠EBA+∠BAE
∴∠CAD=∠ABE
∴
(2)解:由(1)可得
其中AE=
则CD=.
【解析】【分析】(1)利用已知可得到∠DCA=∠BEA=∠CAB=90°,利用同角的余角相等得∠CAD=∠ABE,利用有两组对应角分别相等的两三角形相似,可证得结论;
(2)利用相似三角形的对应边成比例,可得比列式,再结合已知条件可求出CD的长.
23.【答案】(1)解: ∵DP⊥AB,∠C=90°
∴∠C=∠ADP=90°
根据勾股定理可得,AC==4
∵∠A=∠A
∴△APD∽△ABC
∴
∴
∴t=
(2)解: 当△CPQ∽△CAB时,
∴
∴t=
当△CPQ∽△CBA时,
∴
∴t=
【解析】【分析】(1)根据题意,结合勾股定理证明三角形相似,继而由相似三角形的性质计算得到答案即可;
(2)根据相似三角形的对应边成比例,计算得到t的值即可。
一、单选题
1.如图,在△ABC中,如果DE与BC不平行,那么下列条件中,不能判断△ADE∽△ACB的是( )
A.∠ADE=∠C B.∠AED=∠B C. D.
2.若,则a=( )
A. B.1 C.2 D.3
3.下列各组图形中,一定是相似图形的是( )
A.两个等腰梯形 B.两个矩形
C.两个直角三角形 D.两个等边三角形
4.已知两个相似三角形的周长比为,若较大三角形的面积等于,则较小三角形的面积等于( )
A. B. C. D.
5.如图,在 ABCD中,E是AB的中点 ,EC交BD于点F,那么SΔBEF:SΔBCF=( )
A.1:6 B.1:4 C.1:3 D.1:2
6.若△ABC∽△ADE,若AB=9,AC=6,AD=3,则EC的长是( )
A.2 B.3 C.4 D.5
7.两个相似多边形的面积比是9:16,其中较小多边形周长为36cm,则较大多边形周长为( )
A.48cm B.54cm C.56cm D.64cm
8.如图,已知四边形ABCD中,E、F分别为AB、CD 上的两点,且AD∥BC∥EF,AB=4BE,则DF与FC的关系是( )
A.DF=4FC B.DF=3FC C.DF= FC D.DF=2FC
9.在小孔成像问题中,如图所示,若为O到AB的距离是18cm,O到CD的距离是6cm,则像CD的长是物体AB长的( )
A. B. C.2倍 D.3倍
10.如图,在正方形ABCD中,H是对角线BD的中点,延长DC至E,使得DE=DB,连接BE,作DF⊥BE交BC于点G,交BE于点F,连接CH、FH,下列结论:(1)HC=HF;(2)DG=2EF;(3)BE·DF=2CD2;(4)S△BDE=4S△DFH;(5)HF∥DE,正确的个数是( )
A.5 B.4 C.3 D.2
二、填空题
11.如图,若点P是AB的黄金分割点,则线段AP,PB,AB满足关系式 ,即AP是 与 的比例中项.
12.如图,Rt△ABC的边BC在x轴上,点D为斜边AB的中点,AC=3,BC=4,若反比例函数y= 的图象过点A、D,则k的值为 .
13.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长
14.综合实践课上,小慧用两张如图①所示的直角三角形纸片:∠A=90°,AD=2cm,AB=3cm,斜边重合拼成四边形,接着在CB,CD上取点E,F,连AE,BF,使AE⊥BF.
(1)若拼成的四边形如图②所示,则的值为 ;
(2)若拼成的四边形如图③所示,则的值为 .
三、解答题
15.即则称A为a,b的等差中项.如果按一定次序排列的三个数a,G,b满足即=ab(a,b同号),则称G为a,b的等比中项.根据前面给出的概念,求和的等差中项和等比中项.
16.如图,矩形ABCD中,点E为AD上一点,∠BEC=90°,AB=2,DE=1,求BC的长.
17.已知:平行四边形ABCD,E是BA延长线上一点,CE与AD、BD交于G、F.
求证:CF2=GF EF.
18.要做两个形状相同的三角形框架,其中一个三角形的三边长分别为4,5,6,另一个三角形的一边长为2,怎样选料可使这两个三角形相似?请说明理由.
四、综合题
19.如图,已知 是 斜边 上的中线,过点 作 的平行线,过点 作 的垂线,两线相交于点 .
(1)求证: ;
(2)若 , ,求 的面积.
20.如图,在平行四边形 中, 为 上一点, .
(1)求证: ;
(2)若 ,求 的长.
21.在一次关于相似三角形的探究活动中,如图所示: ,老师让大家适当的添上辅助线,看看还能得到哪些相似三角形,小颖连接 、 ,且 、 相交于点 ,于是她得到了 .下面是她的证明过程的一部分,你能帮助她完成证明吗?
(1)证明:∵ ,
∴
∴
又∵
∴
(2)你还能得到图中哪些三角形是相似的?至少写出两对.
22.我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小亮站在距离墙壁1.60米处观察装饰画时的示意图,此时小亮的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直,已知装饰面的高度AD为0.66米.
(1)求证:;
(2)求装饰画顶部到墙壁的距离DC(精确到0.01米).
23.如图,在Rt△ABC中, C=90°,AB=5cm,BC=3cm,D为边AB的中点.P从点A出发,以2cm/s的速度沿A→C→A匀速运动,回到点A时停止运动,同时点Q
从点C出发,以1cm/s的速度沿C→B向终点B匀速运动,连结PQ、DP、DQ.设点P的运动时间为t(s).
(1)当点P沿A→C运动,且DP AB时,求t的值.
(2)当△CPQ与△ABC相似时,求t的值
答案解析部分
1.【答案】D
【解析】【解答】∵∠DAE=∠CAB,
∴当∠AED=∠B或∠ADE=∠C时,△ABC∽△AED;
当 时,△ABC∽△AED.
故答案为:D.
【分析】因为∠A是公共角,所以由∠ADE=∠C(或∠AED=∠B)都可以根据有两个角对应相等的两个三角形相似可得△ABC∽△AED;当时,根据有两边的比相等,且它们的夹角也相等的两个三角形相似可得△ABC∽△AED;当时,不能判断两个三角形相似。
2.【答案】D
【解析】【解答】解:∵ ,
∴3(a-1)=2a,
∴a=3.
故答案为:D.
【分析】根据两内项之积等于两外项之积变为等积式,再去括号、移项、合并同类项即可得出a的值.
3.【答案】D
【解析】【解答】解:A:等腰梯形不一定是相似,不符合题意;
B:矩形不一定相似,不符合题意;
C:直角三角形不一定相似,不符合题意;
D:等边三角形一定相似,符合题意.
故答案为:D
【分析】根据相似图形的定义即可求出答案.
4.【答案】A
【解析】【解答】解:设较小三角形的面积等于,
由题意得:,
解得,
即较小三角形的面积等于,
故答案为:A.
【分析】根据相似三角形的面积比等于相似比的平方即可解答.
5.【答案】D
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴BECD,
∴∠BEC=∠DCF,∠EBF=∠CDF,
∴△EBF∽△CDF,
∴,
△BEF和△BCF分别选择EF、CF为底,则高相同,
∴,
故答案为:D.
【分析】先证明△EBF∽△CDF,可得,再利用等高的三角形的面积关系可得。
6.【答案】C
【解析】【解答】解:∵△ABC∽△ADE,
∴ ,
∵AB=9,AC=6,AD=3,
∴AE=2,
即EC=AC-AE=6-2=4;
故答案为:C.
【分析】利用相似三角形的性质得,对应边的比相等,求出AE的长,EC=AC-AE,即可计算DE的长;
7.【答案】A
【解析】【分析】根据相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方计算即可.
【解答】两个相似多边形的面积比是9:16,
面积比是周长比的平方,
则大多边形与小多边形的相似比是4:3.
相似多边形周长的比等于相似比,
因而设大多边形的周长为xcm,
则有=,
解得:x=48.
大多边形的周长为48cm.
故答案为A.
【点评】本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方
8.【答案】B
【解析】【解答】解:∵ AD∥BC∥EF,
∴,
又∵AB=4BE,
∴DC=4CF,
又∵DC=DF+FC,
∴DF=3FC。
故答案为:B.
【分析】根据平行线分线段成比例定理可得,,结合AB=4BE,可知DC=4FC,据此即可判断。
9.【答案】A
【解析】【解答】解:如图,作OE⊥AB于E,EO的延长线交CD于F.
∵AB∥CD,
∴FO⊥CD,△AOB∽△DOC,
∴ = = = (相似三角形的对应高的比等于相似比),
∴CD= AB,
故选A.
【分析】如图,作OE⊥AB于E,EO的延长线交CD于F.由△AOB∽△DOC,推出 = = = (相似三角形的对应高的比等于相似比),由此即可解决问题.
10.【答案】B
【解析】【解答】解:∵BD=DE,DF⊥BE,
∴EF=BF,
∵H是正方形ABCD对角线BD的中点,
∴CH=DH=BH= BD,
∴HF是△BDE的中位线,
∴HF= DE= BD=CH,HF//DE,故①⑤正确,
∵∠CBE+∠E=90°,∠FDE+∠E=90°,
∴∠CBE=∠FDE,
又∵CD=BC,∠DCG=∠BCE=90°,
∴△BCE≌△DCG,
∴DG=BE,
∵BE=2EF,
∴DG=2EF,故②正确,
∵∠CBE=∠FDE,∠E=∠E,
∴△BCE∽△DFE,
∴ ,即BE·DF=DE·BC,
∵BD2=CD2+BC2=2CD2
∴DE2=2CD2,
∴DE·BC≠2CD2,
∴BE·DF≠2CD2,故③错误,
∵DH= BD,
∴S△DFH= S△DFB,
∵BF= BE,
∴S△DFB= S△BDE,
∴S△DFH= S△BDE,即S△BDE=4S△DFH,故④正确,
综上所述:正确的结论有①②④⑤,共4个,
故答案为:B.
【分析】由等腰三角形“三线合一”的性质可得EF=BF,根据H是正方形对角线BD的中点可得CH=DH=BH,即可证明HF是△BDE的中位线,可得HF= DE,HF//DE;由BD=DE即可得HC=HF;利用直角三角形两锐角互余的关系可得∠CBE=∠CDG,利用ASA可证明△BCE≌△DCG,可得DG=BE,可判定DG=2EF,由正方形的性质可得BD2=2CD2,根据∠CBE=∠CDG,∠E是公共角可证明△BCE∽△DFE,即可得 ,即BE·DF=DE·BC,可对③进行判定,根据等底等高的三角形面积相等可对④进行判定,综上即可得答案.
11.【答案】;PB;AB
【解析】【解答】解:若点P是AB的黄金分割点,则线段AP,PB,AB满足关系式 ,即AP是PB与 AB的比例中项.
故答案为: ,PB、AB.
【分析】根据黄金分割的定义进行填空即可.
12.【答案】6
【解析】【解答】解:作DE⊥x轴于E,如图:
∵∠ACB=90°,
∴DE∥AC,
∴ ,
∴ ,
∵点D为斜边AB的中点,
∴E是BC的中点,即 ,
∴DE= AC= ,
设A(m,3),则D(m+2, ),
∵反比例函数 的图象过点A、D,
∴k=3m=(m+2)× ,
∴m=2,
∴k=3m=6,
故答案为:6.
【分析】作DE⊥x轴于E,利用DE∥AC,可证得△BDE∽△BAC,利用相似三角形的对应边成比例得出 ,利用线段中点的定义求出BE,DE的长;设A(m,3),则D(m+2, ),利用反比例函数图象上的点的坐标特点建立关于m的方程,解方程求出m的值,然后求出k的值.
13.【答案】AD=4
【解析】【解答】
解:∵∠C=∠ADE=90°,∠A=∠A,
∴△ADE∽△ACB,
∴
∴ ,
∴AD=4.
【分析】先证明△ADE∽△ACB,可得,再将数据代入计算即可。
14.【答案】(1)
(2)
【解析】【解答】解:(1)∵, ,
∴.
∵,
∴,
∴.
故答案为: ;
(2)如图,连接AC、BD,且交于点H,设AE、BD交于点G.
由题意四边形ABCD是由两个完全一样的三角形拼成,即A点和C点关于BD对称,
∴, .
∵在 中, ,
∴.
∵,
∴,即
解得: ,
∴.
∵, ,
∴.
∵, , ,
∴,
即在 和 中, ,
∴,
∴.
故答案为: , .
【分析】(1)证明 ,利用相似三角形的性质即可求解;
(2)连接AC、BD,且交于点H,设AE、BD交于点G,先求出BD、AH、AC,再证 ,可得 ,继而得解.
15.【答案】解:和的等差中项为,
和的等比中项为.
【解析】【分析】若a,b,c三个数按这个顺序排列成等差数列,那么b叫a,c的等差中项,且a, b, c满足b-a=c-b;一般地,如果一个数列的首项不为0,且从第二项起,每一项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列;根据等差数列和等比数列定义计算即可求解.
16.【答案】解:∵四边形ABCD为矩形,
∴∠D=90°,DC=AB=2,AD∥BC,
∴∠BEC=∠D,
∵DE=1,
∴EC2=CD2+DE2=5,
∵AD∥BC,
∴∠DEC=∠ECB,
∴△DEC∽△ECB,
∴ ,
∴ .
【解析】【分析】先利用矩形性质得出∠D=90°,DC=AB=2,AD∥BC,然后进一步利用勾股定理得出EC2=CD2+DE2=5,最后证明△DEC∽△ECB,利用相似三角形性质进一步求解即可.
17.【答案】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴=,=,
∴=,
即CF2=GF EF.
【解析】【分析】根据平行四边形的性质得AD∥BC,AB∥CD,再根据平行线分线段成比例定理得=,=,利用等量代换得到=,然后根据比例的性质即可得到结论.
18.【答案】解:设另一个三角形的两条边为x,y,
∵两个三角形是相似三角形,
则,
解得:,;
则,
解得:,;
则,
解得:,;
综上,当三角形的三边为:2,,;或2,,或2,,时,两个三角形是相似三角形.
【解析】【分析】根据题意设另一个三角形的两条边为x,y,结合相似三角形的对应边成比例即可列出相似比的等式,求解即可得出答案.
19.【答案】(1)证明:∵ 为 斜边上的中线,
∴ ,
∴ ,
∵ ,
∴ ,
又∵ ,
∴
(2)解:在 中, , ,
∴ , ,
∵ 为 斜边上的中线,
∴ ,
∵ ,
∴ ,即 ,
∴ .
【解析】【分析】(1)由直角三角形斜边上的中线等于斜边的一半可得CD=AD=AB,根据等边对等角可得∠A=∠ACD,再由平行线的性质可得∠CDE=∠ACD=∠A,于是根据有两对角对应相等的两个三角形相似可得△ABC∽△DEC;
(2)在直角三角形DCE中,用勾股定理可求得DE的长,根据S△DEC=CD.CE可求得三角形的面积;由直角三角形斜边上的中线等于斜边的一半可得AB=2CD,由(1)知,△ABC∽△DEC,根据相似三角形的面积的比等于相似比的平方可得,把AB、DE、S△DEC的值的代入计算即可求解。
20.【答案】(1)证明:∵四边形 是平行四边形,
∴ ,
∴ ,
∵ ,
∴
又∵ ,
∴
(2)解:∵四边形 是平行四边形
∴ ,
由(1)知: ,
∴ ,
∴ ,
∴ ,
∴
【解析】【分析】(1)根据平行四边形的对边平行得出AD∥BC,根据平行线的性质可得 ,从而可得 ,又 ,根据有两组角对应相等的两个三角形相似可得出结论;
(2)根据相似三角形的对应边成比例建立方程,求解即可.
21.【答案】(1);∠A=∠A,
(2)解:△DFB∽△EFC,△BFC∽△DFE.
理由:∵△ACD∽△ABE,
∴∠BDF=∠FEC,
∵∠DFB=∠EFC,
∴△DFB∽△EFC,
∴ ,
∴ ,
∵∠BFC=∠EFD,
∴△BFC∽△DFE
【解析】【解答】解:证明:∵∠A=∠A,∠ACB=∠ADE
∴△ACB∽△ADE
∴
又∵∠A=∠A,
∴△ACD∽△ABE
【分析】(1)根据两边成比例夹角相等两个三角形相似证明即可;(2)相似三角形还有:△DFB∽△EFC,△BFC∽△DFE.
22.【答案】(1)解:由题意可知∠DCA=∠BEA=∠CAB=90°
∵∠CAD+∠BAE=∠EBA+∠BAE
∴∠CAD=∠ABE
∴
(2)解:由(1)可得
其中AE=
则CD=.
【解析】【分析】(1)利用已知可得到∠DCA=∠BEA=∠CAB=90°,利用同角的余角相等得∠CAD=∠ABE,利用有两组对应角分别相等的两三角形相似,可证得结论;
(2)利用相似三角形的对应边成比例,可得比列式,再结合已知条件可求出CD的长.
23.【答案】(1)解: ∵DP⊥AB,∠C=90°
∴∠C=∠ADP=90°
根据勾股定理可得,AC==4
∵∠A=∠A
∴△APD∽△ABC
∴
∴
∴t=
(2)解: 当△CPQ∽△CAB时,
∴
∴t=
当△CPQ∽△CBA时,
∴
∴t=
【解析】【分析】(1)根据题意,结合勾股定理证明三角形相似,继而由相似三角形的性质计算得到答案即可;
(2)根据相似三角形的对应边成比例,计算得到t的值即可。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
