2023—2024学年湘教版九年级数学上册第4章锐角三角函数单元达标测试卷(含解析)
文档属性
| 名称 | 2023—2024学年湘教版九年级数学上册第4章锐角三角函数单元达标测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 626.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 11:10:57 | ||
图片预览



文档简介
湘教版九年级数学上册第4章锐角三角函数单元达标测试卷
一、单选题
1.已知Rt△ABC∽Rt△A'B'C',∠C=∠C'=90°,且AB=2A'B',则sinA与sinA'的关系为( )
A.sinA=2sinA' B.sinA=sinA' C.2sinA=sinA' D.不能确定
2.在中,,则cosB的值为( )
A. B. C. D.
3.在 中, , , ,那么 的值是( )
A. B. C. D.
4.已知,在Rt△ABC中,∠C=90°,AC=3,BC=4,则sinA的值为( )
A. B. C. D.
5.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
A. B. C. D.
6.如图,某学校操场旗杆上高高飘扬着五星红旗,数学小组想测量旗杆的高度,在离旗杆底部4米的处,用高1.5米的测角仪测得旗杆顶点的仰角为,则旗杆的高度为( )米
A. B. C. D.
7.若规定sin(α﹣β)=sinαcosβ﹣cosαsinβ,则sin15°=( )
A. B. C. D.
8.已知∠α的顶点在原点,一条边在x轴的正半轴,另一条边经过点P(3,-4),则sinα的值是 ( )
A. B. C. D.
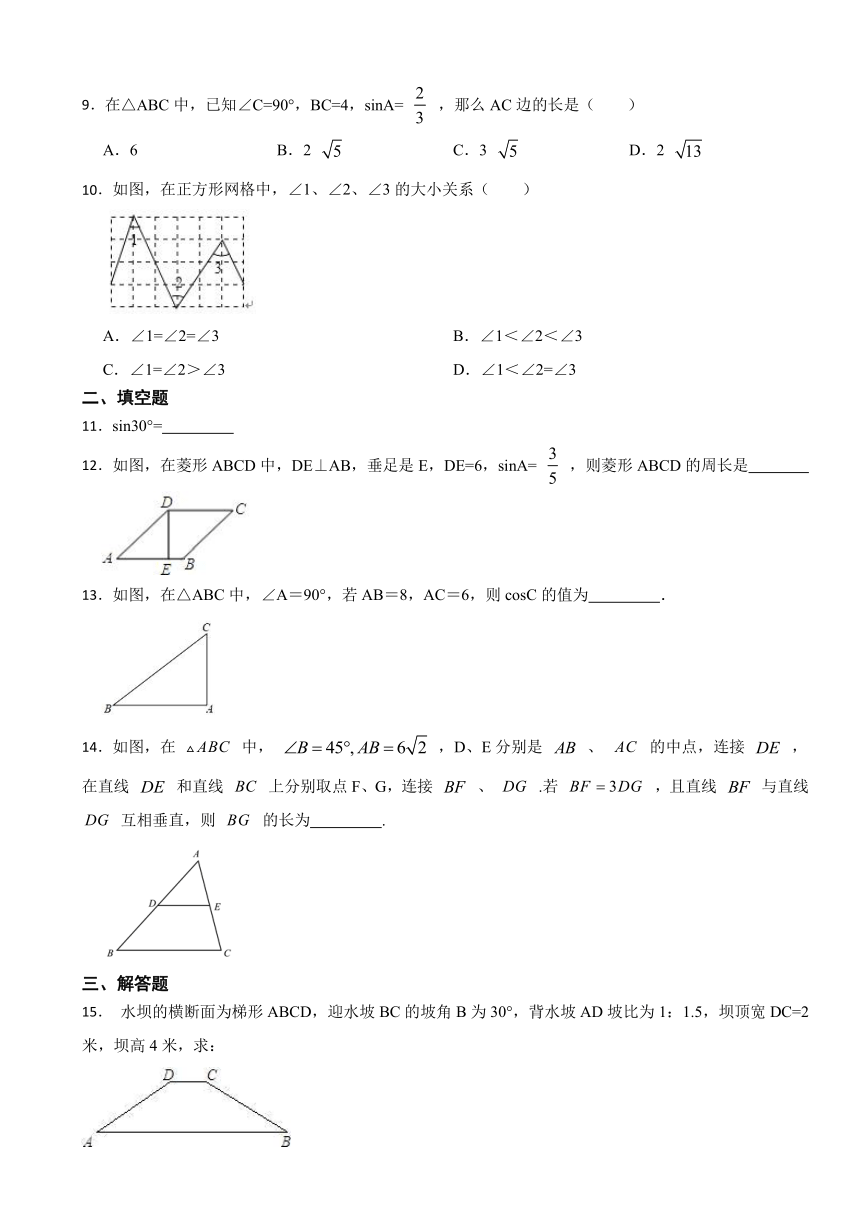
9.在△ABC中,已知∠C=90°,BC=4,sinA= ,那么AC边的长是( )
A.6 B.2 C.3 D.2
10.如图,在正方形网格中,∠1、∠2、∠3的大小关系( )
A.∠1=∠2=∠3 B.∠1<∠2<∠3
C.∠1=∠2>∠3 D.∠1<∠2=∠3
二、填空题
11.sin30°=
12.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sinA= ,则菱形ABCD的周长是
13.如图,在△ABC中,∠A=90°,若AB=8,AC=6,则cosC的值为 .
14.如图,在 中, ,D、E分别是 、 的中点,连接 ,在直线 和直线 上分别取点F、G,连接 、 .若 ,且直线 与直线 互相垂直,则 的长为 .
三、解答题
15. 水坝的横断面为梯形ABCD,迎水坡BC的坡角B为30°,背水坡AD坡比为1:1.5,坝顶宽DC=2米,坝高4米,求:
(1)坝底AB的长;
(2)迎水坡BC的坡比.
16.如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)
17.“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
18.嵩岳寺塔位于登封市区西北6千米嵩山南麓嵩岳寺院内,为北魏时期佛塔.该塔是我国现存最早的砖塔,反映了中外建筑文化交流融合创新的历程,在结构、造型等方面具有很大价值,对后世砖塔建筑有着巨大影响.某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.
课题 测量嵩岳寺塔的高度
测量工具 测量角度的仪器,皮尺等
测量方案 在点C处放置高为1.3米的测角仪CD,此时测得塔顶端A的仰角为45°,再沿BC方向走22米到达点E处,此时测得塔顶端A的仰角为32°. 说明:点E、C、B三点在同一水平线上.
请你根据表中信息结合示意图帮助该数学兴趣小组求嵩岳寺塔AB的高度.(精确到0.1米,参考数据:,,)
四、综合题
19.在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地.
(1)求A地与信号发射塔P之间的距离;
(2)求C地与信号发射塔P之间的距离.(计算结果保留根号)
20.如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求∠D的正切值.
21.身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根5米长的竹竿能否触到挂在树上的风筝?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
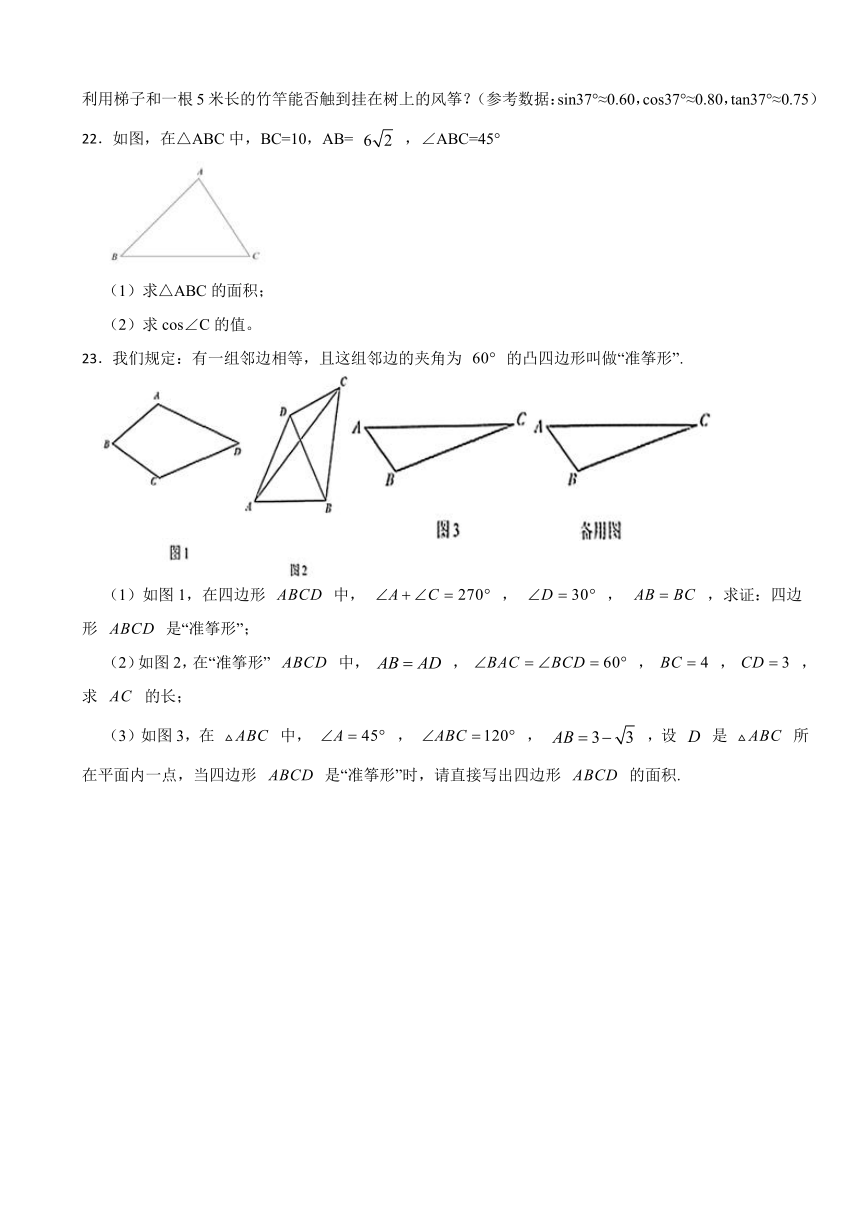
22.如图,在△ABC中,BC=10,AB= ,∠ABC=45°
(1)求△ABC的面积;
(2)求cos∠C的值。
23.我们规定:有一组邻边相等,且这组邻边的夹角为 的凸四边形叫做“准筝形”.
(1)如图1,在四边形 中, , , ,求证:四边形 是“准筝形”;
(2)如图2,在“准筝形” 中, , , , ,求 的长;
(3)如图3,在 中, , , ,设 是 所在平面内一点,当四边形 是“准筝形”时,请直接写出四边形 的面积.
答案解析部分
1.【答案】B
【解析】【解答】解:已知Rt△ABC∽Rt△A'B'C',∠C=∠C'=90°,
∴∠A=∠A',
则sinA=sinA'。
故答案为:B。
【分析】两个角相等,那么这两个角的正弦值是相等的。
2.【答案】C
【解析】【解答】解:在中,,
,
故答案为:C.
【分析】由∠A+∠B=90°,可得sinA=cosB,继而得解.
3.【答案】A
【解析】【解答】在Rt△ABC中,
∵∠C=90°,AB=5,BC=3,
∴AC=4,
∴tanA= .
故答案为:A.
【分析】先利用勾股定理计算出AC,然后根据正切的定义求tanA的值.
4.【答案】D
【解析】【解答】解:由勾股定理得:AB 5,sinA .
故答案为:D.
【分析】首先根据勾股定理算出AB的长,再根据正弦函数的定义,由 sinA=即可求出答案。
5.【答案】B
【解析】【解答】解:在Rt△ABC中,∠C=90°,AC=3,AB=5,由勾股定理,得:
BC= = =4.cosB= = ,
故答案为:B.
【分析】利用勾股定理先求出BC=4,再计算求解即可。
6.【答案】C
【解析】【解答】解:由图可知四边形ABED是矩形,则,,
,
,
=.
故答案为:C.
【分析】利用已知条件可证得四边形ABED是矩形,利用矩形的性质可证得DE=AB,AD=BE,利用解直角三角形表示出CE的长,然后根据BC=BE+CE,代入计算求出BC的长.
7.【答案】D
【解析】【解答】解:由题意得,sin15°=sin(45°﹣30°)
=sin45°cos30°﹣cos45°sin30°
= × ﹣ ×
= ,
故选:D.
【分析】根据题意把15°化为45°﹣30°,代入特殊角的三角函数值计算即可.
8.【答案】C
【解析】【分析】根据三角函数的定义:锐角的正弦为对边比斜边求解.注意先求出斜边.
【解答】设P(3,-4),则过点P向x轴引垂线,垂足为M.
得到Rt△POM,且OM=3,PM=4,
∴OP==5,
∴sinα==.
故选C.
【点评】本题考查锐角三角函数的定义:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比边
9.【答案】B
【解析】【解答】∵在△ABC中,∠C=90°,BC=4,
∴sinA= = = ,
∴AB=6.
∴AC= =2 .
故答案为:B.
【分析】根据在△ABC中的三角函数值,利用直角三角形的勾股定理求出AC的长度。
10.【答案】D
【解析】【解答】解:如图所示:
根据图形可知:
∠CBD=∠BDE,tan∠ABC=,tan∠EDF=,
∴∠ABC<∠EDF
∴∠ABC+∠CBD<∠EDF+∠BDE,即∠1<∠2.
根据图形可知:∠EDF=∠DFG,tan∠BDE=,tan∠GFH=,
∴∠BDE=∠GFH.
∴∠EDF+∠BDE=∠DFG+∠GFH,即:∠2=∠3.
故选:D.
【分析】由平行线的性质可知:∠CBD=∠BDE,∠EDF=∠DFG,然后根据锐角三角形函数的定义可知:tan∠ABC=,tan∠EDF=,tan∠BDE=tan∠GFH=,从而可判定出∠ABC<∠EDF,∠BDE=∠GFH.然后即可比较它们的大小.
11.【答案】
【解析】【解答】根据特殊角的三角函数值计算即可:sin30°= .
【分析】利用特殊角的三角函数值可求出sin30°的值.
12.【答案】40
【解析】【解答】 已知如图DE⊥AB,垂足是E,
所以△AED为直角三角形,
则得:sinA= ,即: = ∴AD=10,
∴菱形ABCD的周长为:10×4=40.
故答案为:40.
【分析】此题考查的知识点是解直角三角形和菱形的性质,解题的关键是先根据直角三角形的性质求出菱形ABCD的边长AD
13.【答案】
【解析】【解答】在△ABC中,∠A=90°,
∵AB=8,AC=6,
∴BC= = =10,
∴cosC= = = ,
故答案为: .
【分析】直接利用已知画出图形,进而利用锐角三角函数关系得出答案。
14.【答案】4或2
【解析】【解答】解:如图,当点F在点D右侧时,
过点F作FM∥DG,交直线BC于点M,过点B作BN⊥DE,交直线DE于点N,
∵D,E分别是AB和AC中点,AB= ,
∴DE∥BC,BD=AD= ,∠FBM=∠BFD,
∴四边形DGMF为平行四边形,
则DG=FM,
∵DG⊥BF,BF=3DG,
∴∠BFM=90°,
∴tan∠FBM= =tan∠BFD,
∴ ,
∵∠ABC=45°=∠BDN,
∴△BDN为等腰直角三角形,
∴BN=DN= ,
∴FN=3BN=9,DF=GM=6,
∵BF= = ,
∴FM= = ,
∴BM= ,
∴BG=10-6=4;
当点F在点D左侧时,过点B作BN⊥DE,交直线DE于N,过点B作BM∥DG,交直线DE于M,延长FB和DG,交点为H,
可知:∠H=∠FBM=90°,四边形BMDG为平行四边形,
∴BG=MD,BM=DG,
∵BF=3DG,
∴tan∠BFD= ,
同理可得:△BDN为等腰直角三角形,BN=DN=3,
∴FN=3BN=9,
∴BF= ,
设MN=x,则MD=3-x,FM=9+x,
在Rt△BFM和Rt△BMN中,
有 ,
即 ,
解得:x=1,即MN=1,
∴BG=MD=ND-MN=2.
综上:BG的值为4或2.
故答案为:4或2.
【分析】分当点F在点D右侧时,当点F在点D左侧时,两种情况,分别画出图形,结合三角函数,勾股定理以及平行四边形的性质求解即可.
15.【答案】解:(1)如图,作CF⊥AB,DE⊥AD,垂足分别为点F,E.∴四边形CDEF是矩形.∴CF=DE=4,EF=CD=2.∴BF=CFcot30°=,AE=1.5DE=6.∴AB=BF+EF+AE=+2+6=+8(2)∵CF=4,BF=,∴迎水坡BC的坡比为:CF/BF=.
【解析】【分析】
(1)作出两条高,得到两个直角三角形及一个矩形.利用勾股定理及坡比得到BF,AE长.
(2)利用坡比的定义,即可得出迎水坡BC的坡比的值.
16.【答案】解:过点A作AE⊥CD于点E,则四边形AEDB是矩形,
∴AB=DE,AE=DB=20米,
在Rt△ADE中,tan45°= ,
∴DE=AE=20,
在Rt△ACE中,tan60°= ,
∴CE=20 ,
∴CD=DE+CE=20+20 ≈55米,
答:大楼AB的高度是20米,大楼CD的高度约为55米.
【解析】【分析】过点A作AE⊥CD于点E,根据正切的定义分别求出DE、CE,结合图形计算即可.
17.【答案】解:∵BN∥ED,∴∠NBD=∠BDE=37°,∵AE⊥DE,∴∠E=90°,∴BE=DE tan∠BDE≈18.75(cm),如图,过C作AE的垂线,垂足为F,∵∠FCA=∠CAM=45°,∴AF=FC=25cm,∵CD∥AE,∴四边形CDEF为矩形,∴CD=EF,∵AE=AB+EB=35.75(cm),∴CD=EF=AE-AF≈10.8(cm),答:线段BE的长约等于18.8cm,线段CD的长约等于10.8cm
【解析】【分析】(1)由BN∥ED可得∠NBD=∠BDE=37°,在直角三角形BED中已知一边一角可求BE的长。(2)过C作AE的垂线,垂足为F,则四边形CDEF为矩形,根据矩形的性质可得CD=EF,CF=DE=25cm,由已知条件可得Rt△AFC是等腰直角三角形,再求出AE和AF的长,即可求出CD的长。
18.【答案】解:如图所示,延长FD到G与AB交于点G,
由题意得:,∠AGD=90°,
∵∠ADG=45°,
∴∠GAD=45°,
∴AG=GD,
设,则,
∵,
∴,
解得,
∴,
∴,
∴嵩岳寺塔的高度约为37.2m.
【解析】【分析】延长FD与AB交于点G, 由题意得BG=CD=EF=1.3m,∠AGD=90°,由∠ADG=45°,得∠GAD=45°,从而得AG=GD,设AG=GD=xm,则GF=(x+22)m,由锐角三角函数关系列出关于x的方程,解得x即AG的长度,再由AB=AG+BG,即可求得嵩岳寺塔的高度.
19.【答案】(1)解:依题意知: , ,
过点B作 于D点,
∵,
∴
∵,
∴
∵
∴
∴
(2)解:∵,
∴
过点P作 于E
∵,
∴
∵
∴,
∵
∴
∴
【解析】【分析】(1)先求出AD=BD=4,再求出PD的值,最后计算求解即可;
(2)先求出∠PBE=60°,再求出CE=8,最后求解即可。
20.【答案】(1)解:∵∠ACB=90°,
∴∠ACF=∠ACB=90°,∠B+∠BAC=90°,
∵AD⊥AB,
∴∠BAC+∠CAF=90°,
∴∠B=∠CAF,
∴△ABC∽△FAC, ∴ ,即 , 解得:CF
(2)解:如图,过点C作CH⊥AB于点H,则AD∥CH,即:∠D=∠ECH, ∵AC=3,BC=4,
∴AB=5,
∴CH ,
∴AH ,EH=AE﹣AH ,
∴tanD=tan∠ECH .
【解析】【分析】(1)由∠ACB=90°,AD⊥AB,易证:△ABC∽△FAC,得: ,即可得到答案;(2)过点C作CH⊥AB于点H,根据面积法,可得:CH ,进而得到:AH ,EH ,根据正切三角函数的定义,即可求解.
21.【答案】(1)解:过A作AP⊥GF于点P,
则AP=BF=12,AB=PF=1.4,∠GAP=37°,
在Rt△PAG中, ,
∴GP=AP tan37°≈12×0.75=9(米).
∴GF=9+1.4≈10.4(米).
(2)解:由题意可知MN=5,MF=3,
∴在直角△MNF中, .
∵10.4﹣5﹣1.65=3.75<4,∴能触到挂在树上的风筝.
【解析】【分析】(1)过A作AP⊥GF于点P.在Rt△PAG中利用三角函数求得GP的长,从而求得GF的长.(2)在Rt△MNF中,利用勾股定理求得NF的长度,NF的长加上身高再加上竹竿长,与GF比较大小即可.
22.【答案】(1)解:过点A作AD⊥BC于点D,则∠ADB=∠ADC=90°。
在Rt△ABD中,AD=AB·sin∠ABC=6×sin45°=6×=6
∴S△ABC的面积=BC·AD=×10×6=30;
(2)解: 在Rt△ABC中,∠ABC=45° ,∴BD=AD=6
∴CD=BC-BD=10-6=4
在Rt△ACD中,AC=
∴cos∠C=
【解析】【分析】(1)作AD⊥BC,则∠ADB=∠ADC=90°。先在Rt△ABD中,利用三角函数的定义求出AD的长,然后利用三角形的面积公式求解即可;
(2)先在Rt△ABC中,由∠ABC=45° 得BD=AD=6,进而求出CD的长,然后在Rt△ACD中,利用勾股定理求出AC的长,进而利用锐角三角函数的定义求出cos∠C即可。
23.【答案】(1)解:在四边形 中,
∵ ,
∴
∵
∴四边形 是“准筝形”
(2)解:如图,以 为边作等边 ,连结
过点E作EF⊥BC于F, 则DE=DC=CE=3,∠CDE=∠DCE=60°,
∵AB=AD,∠BAD=∠BCD=60°,
∴ 是等边三角形,
∴∠ADB=60°,AD=BD,
∴∠ADB+∠BDC=∠CDE+∠BDC,
即∠ADC=∠BDE,
在 和 中,
,
∴ (SAS),
∴AC=BE,
∵∠BCD=∠DCE=60°,
∴∠ECF=180°-60°-60°=60°,
∵∠EFC=90°,
∴∠CEF=30°,
∴CF= CE=
由勾股定理得:
BF=BC+CF=
在Rt 中,由勾股定理得:
∴AC=
(3)解:过点C作CH⊥AB,交AB延长线于H,如图所示: 设BH=x,
∵∠ABC=120°,CH是 的高线,
∴∠BCH=30°,
∴HC= ,BC=2BH=2x,
又∵∠A=45°,
∴ 是等腰直角三角形,
∴HA=HC,
∵AB=
∴ 解得:
∴HC= ,BC=
∴AC=
①当AB=AD= ∠BAD=60°时,
连接BD,过点C作CG⊥BD,交BD延长线于点G,过点A作AK⊥BD,如图所示:
则BD= ∠ABD=60°,BK= AB=
∵∠ABC=120°, ∴∠CBG=60°=∠CBH,
在 和 中,
,
∴ (AAS),
∴GC=HC=3,
在Rt 中,由勾股定理得:
∴
∴
②当BC=CD= ∠BCD=60°时,
连接BD,作CG⊥BD于点G,AK⊥BD于K,
如图所示: 则BD= ,CG=
AK= ,
∴
∴
③当AD=CD=AC= ,∠ADC=60°时, 作DM⊥AC于M,如图所示:
则DM=
∴
∴
综上所述,四边形ABCD的面积为 或 或 .
【解析】【分析】(1)由四边形内角和定理求出∠B=60°,由AB=BC,即可得出结论;(2)以CD为边作等边 ,连接BE,过点E作EF⊥BC于F,证 (SAS),得AC=BE,求出∠CEF=30°,由直角三角形的性质得出CF= 由勾股定理求出EF= 再由勾股定理即可得出答案;(3)过点C作CH⊥AB,交AB延长线于H,设BH=x,求出∠BCH=30°,由直角三角形的性质得出HC= ,BC=2BH=2x,证 是等腰直角三角形,则HA=HC, ,解得 ,进而得出AC的长,分三种情况,①当AB=AD= ∠BAD=60°时,②当BC=CD= ∠BCD=60°时, ③当AD=CD=AC= ,∠ADC=60°时,分别求解即可.
一、单选题
1.已知Rt△ABC∽Rt△A'B'C',∠C=∠C'=90°,且AB=2A'B',则sinA与sinA'的关系为( )
A.sinA=2sinA' B.sinA=sinA' C.2sinA=sinA' D.不能确定
2.在中,,则cosB的值为( )
A. B. C. D.
3.在 中, , , ,那么 的值是( )
A. B. C. D.
4.已知,在Rt△ABC中,∠C=90°,AC=3,BC=4,则sinA的值为( )
A. B. C. D.
5.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
A. B. C. D.
6.如图,某学校操场旗杆上高高飘扬着五星红旗,数学小组想测量旗杆的高度,在离旗杆底部4米的处,用高1.5米的测角仪测得旗杆顶点的仰角为,则旗杆的高度为( )米
A. B. C. D.
7.若规定sin(α﹣β)=sinαcosβ﹣cosαsinβ,则sin15°=( )
A. B. C. D.
8.已知∠α的顶点在原点,一条边在x轴的正半轴,另一条边经过点P(3,-4),则sinα的值是 ( )
A. B. C. D.
9.在△ABC中,已知∠C=90°,BC=4,sinA= ,那么AC边的长是( )
A.6 B.2 C.3 D.2
10.如图,在正方形网格中,∠1、∠2、∠3的大小关系( )
A.∠1=∠2=∠3 B.∠1<∠2<∠3
C.∠1=∠2>∠3 D.∠1<∠2=∠3
二、填空题
11.sin30°=
12.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sinA= ,则菱形ABCD的周长是
13.如图,在△ABC中,∠A=90°,若AB=8,AC=6,则cosC的值为 .
14.如图,在 中, ,D、E分别是 、 的中点,连接 ,在直线 和直线 上分别取点F、G,连接 、 .若 ,且直线 与直线 互相垂直,则 的长为 .
三、解答题
15. 水坝的横断面为梯形ABCD,迎水坡BC的坡角B为30°,背水坡AD坡比为1:1.5,坝顶宽DC=2米,坝高4米,求:
(1)坝底AB的长;
(2)迎水坡BC的坡比.
16.如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)
17.“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
18.嵩岳寺塔位于登封市区西北6千米嵩山南麓嵩岳寺院内,为北魏时期佛塔.该塔是我国现存最早的砖塔,反映了中外建筑文化交流融合创新的历程,在结构、造型等方面具有很大价值,对后世砖塔建筑有着巨大影响.某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.
课题 测量嵩岳寺塔的高度
测量工具 测量角度的仪器,皮尺等
测量方案 在点C处放置高为1.3米的测角仪CD,此时测得塔顶端A的仰角为45°,再沿BC方向走22米到达点E处,此时测得塔顶端A的仰角为32°. 说明:点E、C、B三点在同一水平线上.
请你根据表中信息结合示意图帮助该数学兴趣小组求嵩岳寺塔AB的高度.(精确到0.1米,参考数据:,,)
四、综合题
19.在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地.
(1)求A地与信号发射塔P之间的距离;
(2)求C地与信号发射塔P之间的距离.(计算结果保留根号)
20.如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求∠D的正切值.
21.身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根5米长的竹竿能否触到挂在树上的风筝?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
22.如图,在△ABC中,BC=10,AB= ,∠ABC=45°
(1)求△ABC的面积;
(2)求cos∠C的值。
23.我们规定:有一组邻边相等,且这组邻边的夹角为 的凸四边形叫做“准筝形”.
(1)如图1,在四边形 中, , , ,求证:四边形 是“准筝形”;
(2)如图2,在“准筝形” 中, , , , ,求 的长;
(3)如图3,在 中, , , ,设 是 所在平面内一点,当四边形 是“准筝形”时,请直接写出四边形 的面积.
答案解析部分
1.【答案】B
【解析】【解答】解:已知Rt△ABC∽Rt△A'B'C',∠C=∠C'=90°,
∴∠A=∠A',
则sinA=sinA'。
故答案为:B。
【分析】两个角相等,那么这两个角的正弦值是相等的。
2.【答案】C
【解析】【解答】解:在中,,
,
故答案为:C.
【分析】由∠A+∠B=90°,可得sinA=cosB,继而得解.
3.【答案】A
【解析】【解答】在Rt△ABC中,
∵∠C=90°,AB=5,BC=3,
∴AC=4,
∴tanA= .
故答案为:A.
【分析】先利用勾股定理计算出AC,然后根据正切的定义求tanA的值.
4.【答案】D
【解析】【解答】解:由勾股定理得:AB 5,sinA .
故答案为:D.
【分析】首先根据勾股定理算出AB的长,再根据正弦函数的定义,由 sinA=即可求出答案。
5.【答案】B
【解析】【解答】解:在Rt△ABC中,∠C=90°,AC=3,AB=5,由勾股定理,得:
BC= = =4.cosB= = ,
故答案为:B.
【分析】利用勾股定理先求出BC=4,再计算求解即可。
6.【答案】C
【解析】【解答】解:由图可知四边形ABED是矩形,则,,
,
,
=.
故答案为:C.
【分析】利用已知条件可证得四边形ABED是矩形,利用矩形的性质可证得DE=AB,AD=BE,利用解直角三角形表示出CE的长,然后根据BC=BE+CE,代入计算求出BC的长.
7.【答案】D
【解析】【解答】解:由题意得,sin15°=sin(45°﹣30°)
=sin45°cos30°﹣cos45°sin30°
= × ﹣ ×
= ,
故选:D.
【分析】根据题意把15°化为45°﹣30°,代入特殊角的三角函数值计算即可.
8.【答案】C
【解析】【分析】根据三角函数的定义:锐角的正弦为对边比斜边求解.注意先求出斜边.
【解答】设P(3,-4),则过点P向x轴引垂线,垂足为M.
得到Rt△POM,且OM=3,PM=4,
∴OP==5,
∴sinα==.
故选C.
【点评】本题考查锐角三角函数的定义:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比边
9.【答案】B
【解析】【解答】∵在△ABC中,∠C=90°,BC=4,
∴sinA= = = ,
∴AB=6.
∴AC= =2 .
故答案为:B.
【分析】根据在△ABC中的三角函数值,利用直角三角形的勾股定理求出AC的长度。
10.【答案】D
【解析】【解答】解:如图所示:
根据图形可知:
∠CBD=∠BDE,tan∠ABC=,tan∠EDF=,
∴∠ABC<∠EDF
∴∠ABC+∠CBD<∠EDF+∠BDE,即∠1<∠2.
根据图形可知:∠EDF=∠DFG,tan∠BDE=,tan∠GFH=,
∴∠BDE=∠GFH.
∴∠EDF+∠BDE=∠DFG+∠GFH,即:∠2=∠3.
故选:D.
【分析】由平行线的性质可知:∠CBD=∠BDE,∠EDF=∠DFG,然后根据锐角三角形函数的定义可知:tan∠ABC=,tan∠EDF=,tan∠BDE=tan∠GFH=,从而可判定出∠ABC<∠EDF,∠BDE=∠GFH.然后即可比较它们的大小.
11.【答案】
【解析】【解答】根据特殊角的三角函数值计算即可:sin30°= .
【分析】利用特殊角的三角函数值可求出sin30°的值.
12.【答案】40
【解析】【解答】 已知如图DE⊥AB,垂足是E,
所以△AED为直角三角形,
则得:sinA= ,即: = ∴AD=10,
∴菱形ABCD的周长为:10×4=40.
故答案为:40.
【分析】此题考查的知识点是解直角三角形和菱形的性质,解题的关键是先根据直角三角形的性质求出菱形ABCD的边长AD
13.【答案】
【解析】【解答】在△ABC中,∠A=90°,
∵AB=8,AC=6,
∴BC= = =10,
∴cosC= = = ,
故答案为: .
【分析】直接利用已知画出图形,进而利用锐角三角函数关系得出答案。
14.【答案】4或2
【解析】【解答】解:如图,当点F在点D右侧时,
过点F作FM∥DG,交直线BC于点M,过点B作BN⊥DE,交直线DE于点N,
∵D,E分别是AB和AC中点,AB= ,
∴DE∥BC,BD=AD= ,∠FBM=∠BFD,
∴四边形DGMF为平行四边形,
则DG=FM,
∵DG⊥BF,BF=3DG,
∴∠BFM=90°,
∴tan∠FBM= =tan∠BFD,
∴ ,
∵∠ABC=45°=∠BDN,
∴△BDN为等腰直角三角形,
∴BN=DN= ,
∴FN=3BN=9,DF=GM=6,
∵BF= = ,
∴FM= = ,
∴BM= ,
∴BG=10-6=4;
当点F在点D左侧时,过点B作BN⊥DE,交直线DE于N,过点B作BM∥DG,交直线DE于M,延长FB和DG,交点为H,
可知:∠H=∠FBM=90°,四边形BMDG为平行四边形,
∴BG=MD,BM=DG,
∵BF=3DG,
∴tan∠BFD= ,
同理可得:△BDN为等腰直角三角形,BN=DN=3,
∴FN=3BN=9,
∴BF= ,
设MN=x,则MD=3-x,FM=9+x,
在Rt△BFM和Rt△BMN中,
有 ,
即 ,
解得:x=1,即MN=1,
∴BG=MD=ND-MN=2.
综上:BG的值为4或2.
故答案为:4或2.
【分析】分当点F在点D右侧时,当点F在点D左侧时,两种情况,分别画出图形,结合三角函数,勾股定理以及平行四边形的性质求解即可.
15.【答案】解:(1)如图,作CF⊥AB,DE⊥AD,垂足分别为点F,E.∴四边形CDEF是矩形.∴CF=DE=4,EF=CD=2.∴BF=CFcot30°=,AE=1.5DE=6.∴AB=BF+EF+AE=+2+6=+8(2)∵CF=4,BF=,∴迎水坡BC的坡比为:CF/BF=.
【解析】【分析】
(1)作出两条高,得到两个直角三角形及一个矩形.利用勾股定理及坡比得到BF,AE长.
(2)利用坡比的定义,即可得出迎水坡BC的坡比的值.
16.【答案】解:过点A作AE⊥CD于点E,则四边形AEDB是矩形,
∴AB=DE,AE=DB=20米,
在Rt△ADE中,tan45°= ,
∴DE=AE=20,
在Rt△ACE中,tan60°= ,
∴CE=20 ,
∴CD=DE+CE=20+20 ≈55米,
答:大楼AB的高度是20米,大楼CD的高度约为55米.
【解析】【分析】过点A作AE⊥CD于点E,根据正切的定义分别求出DE、CE,结合图形计算即可.
17.【答案】解:∵BN∥ED,∴∠NBD=∠BDE=37°,∵AE⊥DE,∴∠E=90°,∴BE=DE tan∠BDE≈18.75(cm),如图,过C作AE的垂线,垂足为F,∵∠FCA=∠CAM=45°,∴AF=FC=25cm,∵CD∥AE,∴四边形CDEF为矩形,∴CD=EF,∵AE=AB+EB=35.75(cm),∴CD=EF=AE-AF≈10.8(cm),答:线段BE的长约等于18.8cm,线段CD的长约等于10.8cm
【解析】【分析】(1)由BN∥ED可得∠NBD=∠BDE=37°,在直角三角形BED中已知一边一角可求BE的长。(2)过C作AE的垂线,垂足为F,则四边形CDEF为矩形,根据矩形的性质可得CD=EF,CF=DE=25cm,由已知条件可得Rt△AFC是等腰直角三角形,再求出AE和AF的长,即可求出CD的长。
18.【答案】解:如图所示,延长FD到G与AB交于点G,
由题意得:,∠AGD=90°,
∵∠ADG=45°,
∴∠GAD=45°,
∴AG=GD,
设,则,
∵,
∴,
解得,
∴,
∴,
∴嵩岳寺塔的高度约为37.2m.
【解析】【分析】延长FD与AB交于点G, 由题意得BG=CD=EF=1.3m,∠AGD=90°,由∠ADG=45°,得∠GAD=45°,从而得AG=GD,设AG=GD=xm,则GF=(x+22)m,由锐角三角函数关系列出关于x的方程,解得x即AG的长度,再由AB=AG+BG,即可求得嵩岳寺塔的高度.
19.【答案】(1)解:依题意知: , ,
过点B作 于D点,
∵,
∴
∵,
∴
∵
∴
∴
(2)解:∵,
∴
过点P作 于E
∵,
∴
∵
∴,
∵
∴
∴
【解析】【分析】(1)先求出AD=BD=4,再求出PD的值,最后计算求解即可;
(2)先求出∠PBE=60°,再求出CE=8,最后求解即可。
20.【答案】(1)解:∵∠ACB=90°,
∴∠ACF=∠ACB=90°,∠B+∠BAC=90°,
∵AD⊥AB,
∴∠BAC+∠CAF=90°,
∴∠B=∠CAF,
∴△ABC∽△FAC, ∴ ,即 , 解得:CF
(2)解:如图,过点C作CH⊥AB于点H,则AD∥CH,即:∠D=∠ECH, ∵AC=3,BC=4,
∴AB=5,
∴CH ,
∴AH ,EH=AE﹣AH ,
∴tanD=tan∠ECH .
【解析】【分析】(1)由∠ACB=90°,AD⊥AB,易证:△ABC∽△FAC,得: ,即可得到答案;(2)过点C作CH⊥AB于点H,根据面积法,可得:CH ,进而得到:AH ,EH ,根据正切三角函数的定义,即可求解.
21.【答案】(1)解:过A作AP⊥GF于点P,
则AP=BF=12,AB=PF=1.4,∠GAP=37°,
在Rt△PAG中, ,
∴GP=AP tan37°≈12×0.75=9(米).
∴GF=9+1.4≈10.4(米).
(2)解:由题意可知MN=5,MF=3,
∴在直角△MNF中, .
∵10.4﹣5﹣1.65=3.75<4,∴能触到挂在树上的风筝.
【解析】【分析】(1)过A作AP⊥GF于点P.在Rt△PAG中利用三角函数求得GP的长,从而求得GF的长.(2)在Rt△MNF中,利用勾股定理求得NF的长度,NF的长加上身高再加上竹竿长,与GF比较大小即可.
22.【答案】(1)解:过点A作AD⊥BC于点D,则∠ADB=∠ADC=90°。
在Rt△ABD中,AD=AB·sin∠ABC=6×sin45°=6×=6
∴S△ABC的面积=BC·AD=×10×6=30;
(2)解: 在Rt△ABC中,∠ABC=45° ,∴BD=AD=6
∴CD=BC-BD=10-6=4
在Rt△ACD中,AC=
∴cos∠C=
【解析】【分析】(1)作AD⊥BC,则∠ADB=∠ADC=90°。先在Rt△ABD中,利用三角函数的定义求出AD的长,然后利用三角形的面积公式求解即可;
(2)先在Rt△ABC中,由∠ABC=45° 得BD=AD=6,进而求出CD的长,然后在Rt△ACD中,利用勾股定理求出AC的长,进而利用锐角三角函数的定义求出cos∠C即可。
23.【答案】(1)解:在四边形 中,
∵ ,
∴
∵
∴四边形 是“准筝形”
(2)解:如图,以 为边作等边 ,连结
过点E作EF⊥BC于F, 则DE=DC=CE=3,∠CDE=∠DCE=60°,
∵AB=AD,∠BAD=∠BCD=60°,
∴ 是等边三角形,
∴∠ADB=60°,AD=BD,
∴∠ADB+∠BDC=∠CDE+∠BDC,
即∠ADC=∠BDE,
在 和 中,
,
∴ (SAS),
∴AC=BE,
∵∠BCD=∠DCE=60°,
∴∠ECF=180°-60°-60°=60°,
∵∠EFC=90°,
∴∠CEF=30°,
∴CF= CE=
由勾股定理得:
BF=BC+CF=
在Rt 中,由勾股定理得:
∴AC=
(3)解:过点C作CH⊥AB,交AB延长线于H,如图所示: 设BH=x,
∵∠ABC=120°,CH是 的高线,
∴∠BCH=30°,
∴HC= ,BC=2BH=2x,
又∵∠A=45°,
∴ 是等腰直角三角形,
∴HA=HC,
∵AB=
∴ 解得:
∴HC= ,BC=
∴AC=
①当AB=AD= ∠BAD=60°时,
连接BD,过点C作CG⊥BD,交BD延长线于点G,过点A作AK⊥BD,如图所示:
则BD= ∠ABD=60°,BK= AB=
∵∠ABC=120°, ∴∠CBG=60°=∠CBH,
在 和 中,
,
∴ (AAS),
∴GC=HC=3,
在Rt 中,由勾股定理得:
∴
∴
②当BC=CD= ∠BCD=60°时,
连接BD,作CG⊥BD于点G,AK⊥BD于K,
如图所示: 则BD= ,CG=
AK= ,
∴
∴
③当AD=CD=AC= ,∠ADC=60°时, 作DM⊥AC于M,如图所示:
则DM=
∴
∴
综上所述,四边形ABCD的面积为 或 或 .
【解析】【分析】(1)由四边形内角和定理求出∠B=60°,由AB=BC,即可得出结论;(2)以CD为边作等边 ,连接BE,过点E作EF⊥BC于F,证 (SAS),得AC=BE,求出∠CEF=30°,由直角三角形的性质得出CF= 由勾股定理求出EF= 再由勾股定理即可得出答案;(3)过点C作CH⊥AB,交AB延长线于H,设BH=x,求出∠BCH=30°,由直角三角形的性质得出HC= ,BC=2BH=2x,证 是等腰直角三角形,则HA=HC, ,解得 ,进而得出AC的长,分三种情况,①当AB=AD= ∠BAD=60°时,②当BC=CD= ∠BCD=60°时, ③当AD=CD=AC= ,∠ADC=60°时,分别求解即可.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
