期末复习巩固提升练习(直线与圆的位置关系问题专题巩固)2023~2024学年苏科版数学九年级上册(无答案)
文档属性
| 名称 | 期末复习巩固提升练习(直线与圆的位置关系问题专题巩固)2023~2024学年苏科版数学九年级上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 533.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 12:38:51 | ||
图片预览

文档简介
2023-2024学年苏科版数学九年级上册
期末复习巩固提升练习
(直线与圆的位置关系问题专题巩固)
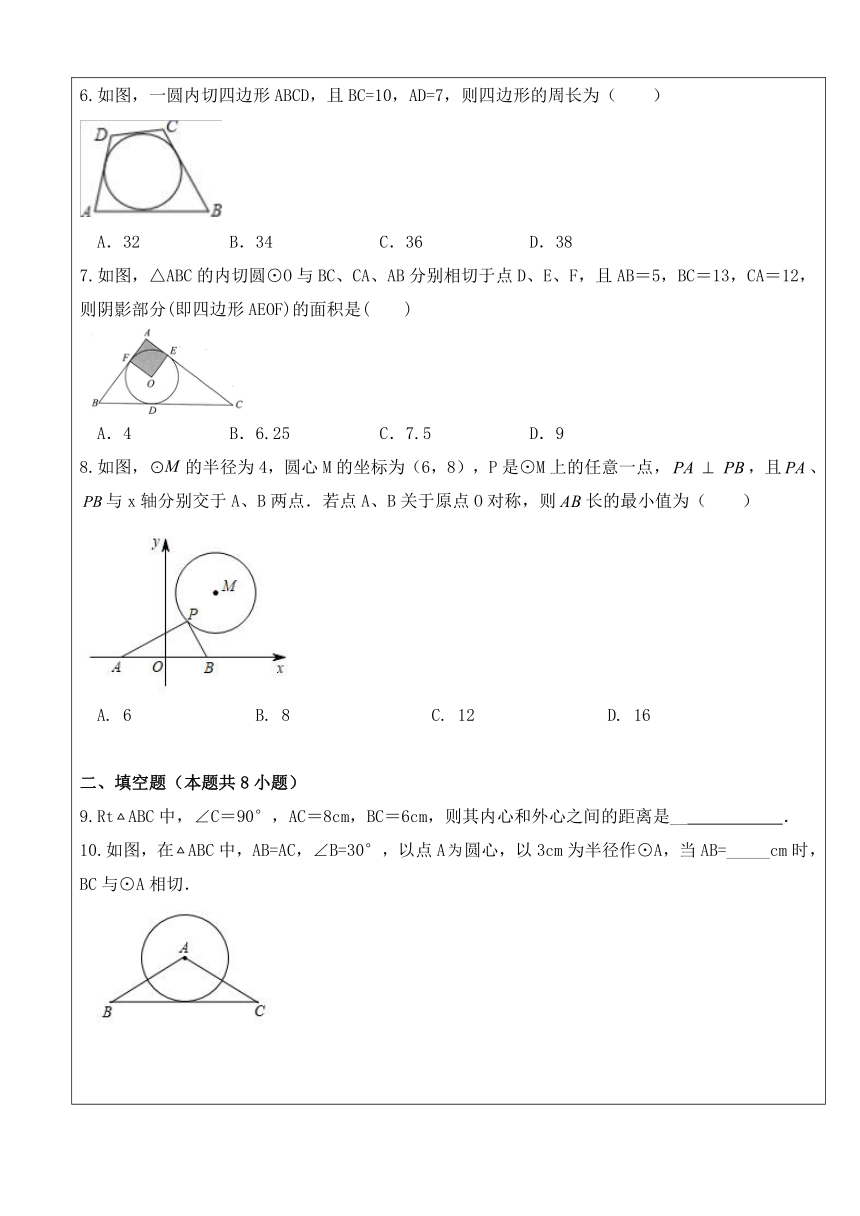
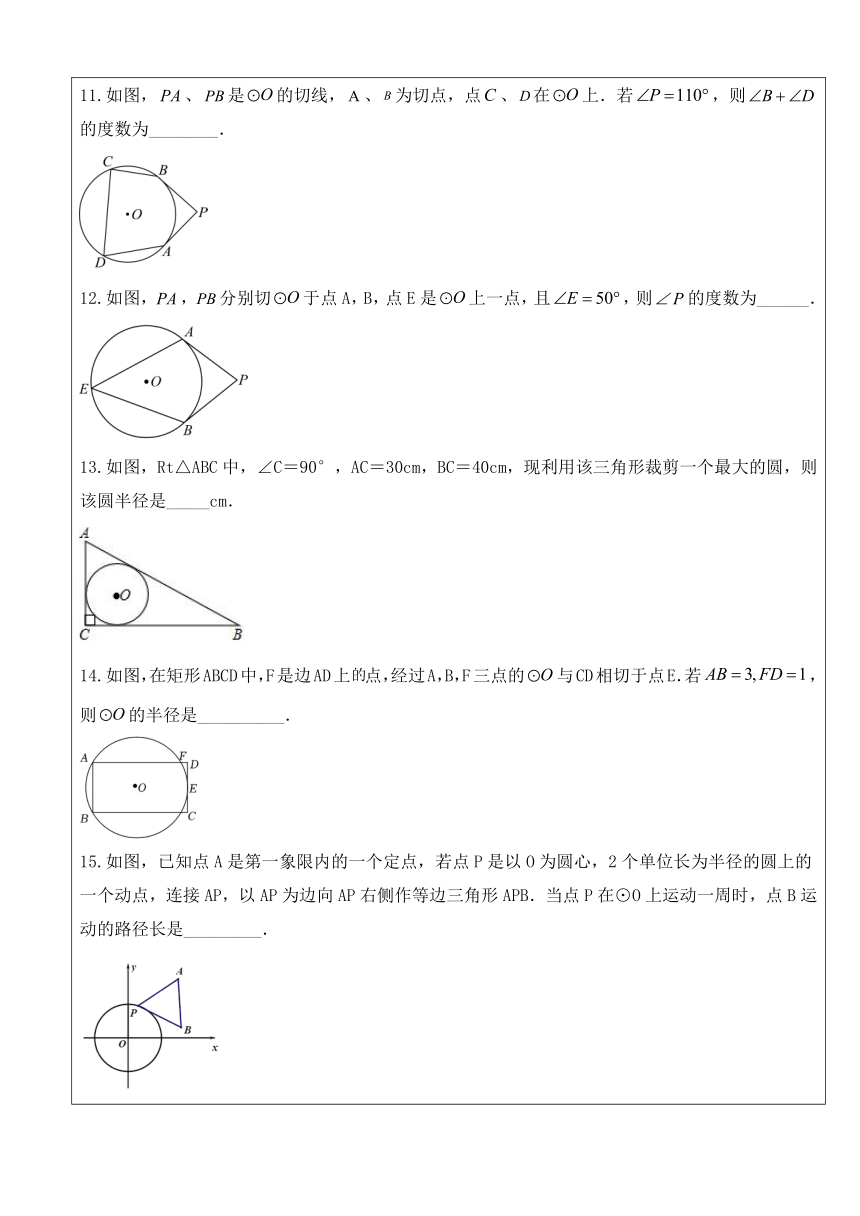
选择题(本题共8小题) 1.已知⊙O直径为4,点O到直线m的距离为2,则直线m与⊙O的位置关系是( ) A.相交 B. 相切 C. 相离 D. 无法判断 2.的半径为5,点A到圆心O的距离为d,已知点A在的外部,则( ) A. B. C. D. 3.如图,PA、PB是⊙O的两条切线, A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于( ) A. B.1 C.2 D. 4.如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( ) A. 35° B. 40° C. 45° D. 50° 5.如图,AB、AC是圆O的两条切线,切点为B、C且∠BAC=50°,D是优弧BDC上一动点(不与B、C重合),则∠BDC的度数为( ) A. 130° B. 65° C. 50°或130° D. 65°或115° 6.如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为( ) A.32 B.34 C.36 D.38 7.如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( ) A.4 B.6.25 C.7.5 D.9 8.如图,的半径为4,圆心M的坐标为(6,8),P是⊙M上的任意一点,,且、与x轴分别交于A、B两点.若点A、B关于原点O对称,则长的最小值为( ) A. 6 B. 8 C. 12 D. 16 填空题(本题共8小题) 9.RtABC中,∠C=90°,AC=8cm,BC=6cm,则其内心和外心之间的距离是__ . 10.如图,在ABC中,AB=AC,∠B=30°,以点A圆心,以3cm为半径作⊙A,当AB=_____cm时,BC与⊙A相切. 11.如图,、是的切线,、为切点,点、在上.若,则的度数为________. 12.如图,,分别切于点A,B,点E是上一点,且,则的度数为______. 13.如图,Rt△ABC中,∠C=90°,AC=30cm,BC=40cm,现利用该三角形裁剪一个最大的圆,则该圆半径是_____cm. 14.如图,在矩形ABCD中,F是边AD上点,经过A,B,F三点的与CD相切于点E.若,则的半径是__________. 15.如图,已知点A是第一象限内的一个定点,若点P是以O为圆心,2个单位长为半径的圆上的一个动点,连接AP,以AP为边向AP右侧作等边三角形APB.当点P在⊙O上运动一周时,点B运动的路径长是_________. 16.如图,直线、相交于点O,,半径为的的圆心在直线上,且与点O的距离为.如果以的速度,沿由A向B的方向移动,那么 _____秒钟后与直线相切. 解答题(本题共8小题) 17.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB. (1)求证:DC为⊙O的切线; (2)若∠DAB=60°,⊙O的半径为3,求线段AC的长. 18.如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA. (1)求∠DOA的度数; (2)求证:直线ED与⊙O相切. 19.如图,是圆的弦,是圆外一点,,交于点,交圆于点,且. (1)判断直线与圆的位置关系,并说明理由; (2)若,,求图中阴影部分的面积. 20.已知是的直径,点是圆上一点,点为外一点,为的切线,. (1)求证:; (2)如果,求图中阴影部分面积. 21.如图,为的直径,,为弦,,为延长线上的点,. (1)求证:是的切线; (2)若的半径为6,求图中阴影部分的面积. 22. 如图,在中,,点D在上,,过A、D两点的圆的圆心O在上. (1)判断所在直线与位置关系,并证明你的结论; (2)若,,求图中阴影部分面积. 23.已知,分别与相切于点,,,为上一点. (1)如图①,求的大小; (2)如图②,为的直径,与相交于点,若,求的大小. 24.如图,以的边上一点为圆心的圆,经过,两点,且与边交于点,为的下半圆弧的中点,连接交于,若. (1)求证:是的切线; (2)若,,求的半径; (3)过点B作的切线交的延长线于,如果连接,将线段以直线为对称轴作对称线段,点正好落在上,连接,请直接写出四边形的形状.
期末复习巩固提升练习
(直线与圆的位置关系问题专题巩固)
选择题(本题共8小题) 1.已知⊙O直径为4,点O到直线m的距离为2,则直线m与⊙O的位置关系是( ) A.相交 B. 相切 C. 相离 D. 无法判断 2.的半径为5,点A到圆心O的距离为d,已知点A在的外部,则( ) A. B. C. D. 3.如图,PA、PB是⊙O的两条切线, A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于( ) A. B.1 C.2 D. 4.如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( ) A. 35° B. 40° C. 45° D. 50° 5.如图,AB、AC是圆O的两条切线,切点为B、C且∠BAC=50°,D是优弧BDC上一动点(不与B、C重合),则∠BDC的度数为( ) A. 130° B. 65° C. 50°或130° D. 65°或115° 6.如图,一圆内切四边形ABCD,且BC=10,AD=7,则四边形的周长为( ) A.32 B.34 C.36 D.38 7.如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( ) A.4 B.6.25 C.7.5 D.9 8.如图,的半径为4,圆心M的坐标为(6,8),P是⊙M上的任意一点,,且、与x轴分别交于A、B两点.若点A、B关于原点O对称,则长的最小值为( ) A. 6 B. 8 C. 12 D. 16 填空题(本题共8小题) 9.RtABC中,∠C=90°,AC=8cm,BC=6cm,则其内心和外心之间的距离是__ . 10.如图,在ABC中,AB=AC,∠B=30°,以点A圆心,以3cm为半径作⊙A,当AB=_____cm时,BC与⊙A相切. 11.如图,、是的切线,、为切点,点、在上.若,则的度数为________. 12.如图,,分别切于点A,B,点E是上一点,且,则的度数为______. 13.如图,Rt△ABC中,∠C=90°,AC=30cm,BC=40cm,现利用该三角形裁剪一个最大的圆,则该圆半径是_____cm. 14.如图,在矩形ABCD中,F是边AD上点,经过A,B,F三点的与CD相切于点E.若,则的半径是__________. 15.如图,已知点A是第一象限内的一个定点,若点P是以O为圆心,2个单位长为半径的圆上的一个动点,连接AP,以AP为边向AP右侧作等边三角形APB.当点P在⊙O上运动一周时,点B运动的路径长是_________. 16.如图,直线、相交于点O,,半径为的的圆心在直线上,且与点O的距离为.如果以的速度,沿由A向B的方向移动,那么 _____秒钟后与直线相切. 解答题(本题共8小题) 17.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB. (1)求证:DC为⊙O的切线; (2)若∠DAB=60°,⊙O的半径为3,求线段AC的长. 18.如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA. (1)求∠DOA的度数; (2)求证:直线ED与⊙O相切. 19.如图,是圆的弦,是圆外一点,,交于点,交圆于点,且. (1)判断直线与圆的位置关系,并说明理由; (2)若,,求图中阴影部分的面积. 20.已知是的直径,点是圆上一点,点为外一点,为的切线,. (1)求证:; (2)如果,求图中阴影部分面积. 21.如图,为的直径,,为弦,,为延长线上的点,. (1)求证:是的切线; (2)若的半径为6,求图中阴影部分的面积. 22. 如图,在中,,点D在上,,过A、D两点的圆的圆心O在上. (1)判断所在直线与位置关系,并证明你的结论; (2)若,,求图中阴影部分面积. 23.已知,分别与相切于点,,,为上一点. (1)如图①,求的大小; (2)如图②,为的直径,与相交于点,若,求的大小. 24.如图,以的边上一点为圆心的圆,经过,两点,且与边交于点,为的下半圆弧的中点,连接交于,若. (1)求证:是的切线; (2)若,,求的半径; (3)过点B作的切线交的延长线于,如果连接,将线段以直线为对称轴作对称线段,点正好落在上,连接,请直接写出四边形的形状.
同课章节目录
