北师大版八年级数学上册 7.5三角形内角和定理 课后专题练习(无答案)
文档属性
| 名称 | 北师大版八年级数学上册 7.5三角形内角和定理 课后专题练习(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 586.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 11:48:54 | ||
图片预览



文档简介
北师大版八年级数学上册 7.5三角形内角和定理课后专题练习
班级:________ 姓名:________
一、单选题(共 10 小题)
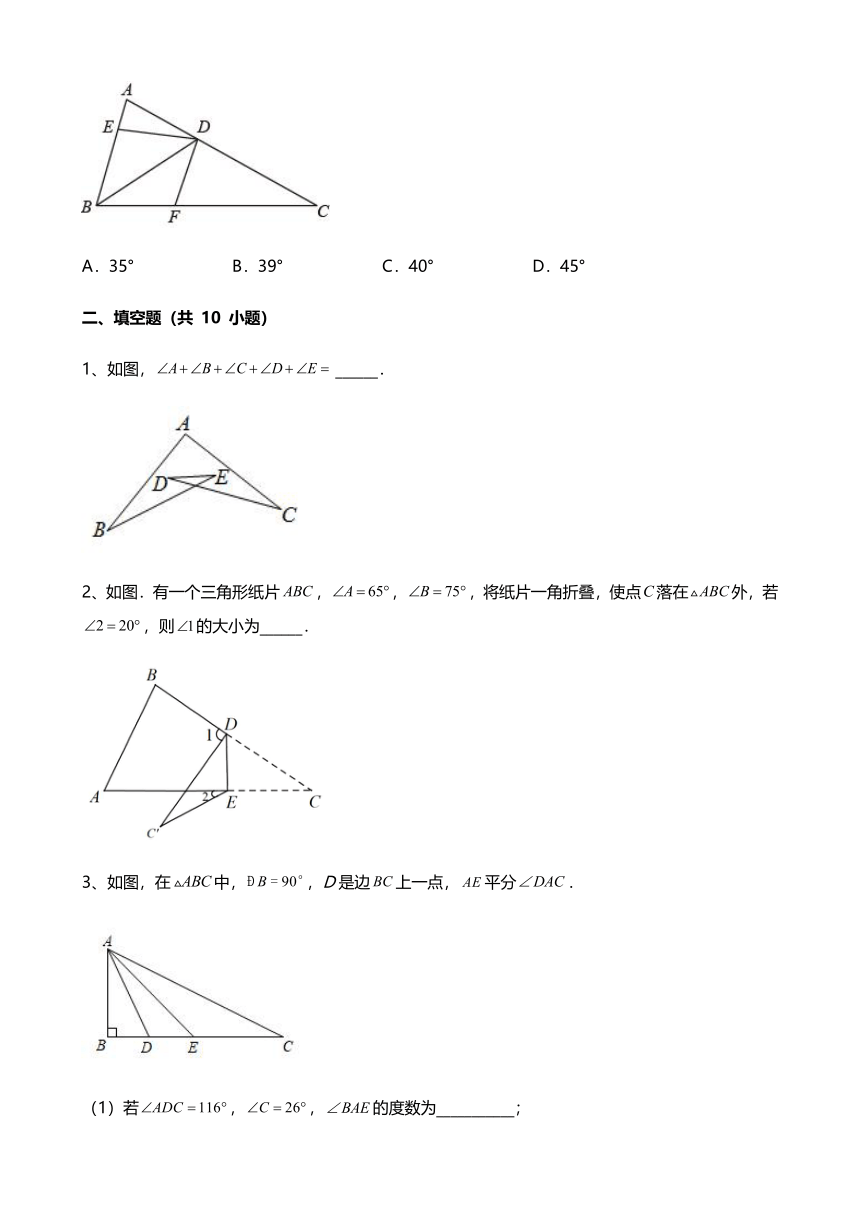
1、如图,中,分别是边上的点,连接,将沿着者折叠,得到,当的三边与的三边有一组边平行时,的度数不可能是( )
A. B. C. D.
2、如图,△ABC中∠A=40°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,点C恰好落在BE上的点G处,此时∠BDC=82°,则原三角形的∠B的度数为( )
A.57° B.60° C.63° D.70°
3、若△ABC三个角的大小满足条件∠A:∠B:∠C=1:3:4,则∠C的大小为( )
A.22.5° B.45° C.67.5° D.90°
4、如图,,,则、和的关系是( )
B.
C. D.
5、如图,把沿线段折叠,使点落在点处;若,,,则的度数为( )
A. B. C. D.
6、如图,在三角形ABC中,,,D是BC上一点,将三角形ABD沿AD翻折后得到三角形AED,边AE交射线BC于点F,若,则( )
A.120° B.135° C.110° D.150°
7、如图,把△ABC沿EF对折,折叠后的图形如图所示,,,则 的度数为( )
A. B. C. D.
8、如图7,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F=135°,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9、如图,的两条角平分线,交于点,若,则为( )
A.112° B.115° C.120° D.125°
10、如图,在△ABC中,∠A=78°,∠EBD=∠EDB,DF平分∠EDC,则∠BDF的度数为( )
A.35° B.39° C.40° D.45°
二、填空题(共 10 小题)
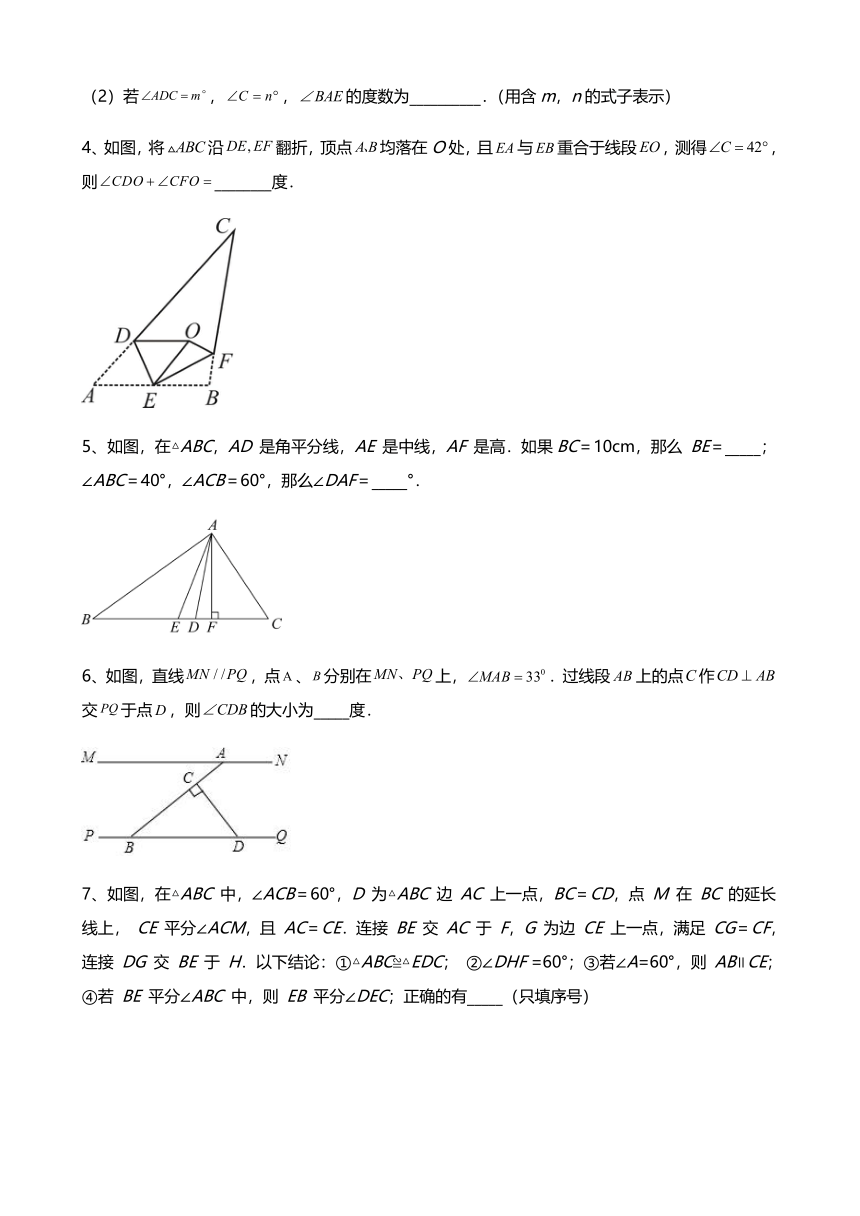
1、如图,______.
2、如图.有一个三角形纸片,,,将纸片一角折叠,使点落在外,若,则的大小为______.
3、如图,在中,,D是边上一点,平分.
(1)若,,的度数为___________;
(2)若,,的度数为__________.(用含m,n的式子表示)
4、如图,将沿翻折,顶点均落在O处,且与重合于线段,测得,则________度.
5、如图,在△ABC,AD 是角平分线,AE 是中线,AF 是高.如果BC=10cm,那么 BE=_____;∠ABC=40°,∠ACB=60°,那么∠DAF=_____°.
6、如图,直线,点、分别在上,.过线段上的点作交于点,则的大小为_____度.
7、如图,在△ABC 中,∠ACB=60°,D 为△ABC 边 AC 上一点,BC=CD,点 M 在 BC 的延长线上, CE 平分∠ACM,且 AC=CE.连接 BE 交 AC 于 F,G 为边 CE 上一点,满足 CG=CF,连接 DG 交 BE 于 H.以下结论:①△ABC≌△EDC; ②∠DHF =60°;③若∠A=60°,则 AB∥CE;④若 BE 平分∠ABC 中,则 EB 平分∠DEC;正确的有_____(只填序号)
8、如图,在四边形ABCD中,∠BCD=50°,∠B=∠D=90°,在BC、CD上分别取一点M、N,使△AMN的周长最小,则∠MAN=_____°.
9、如图所示,△中,,BP,CP,BM,CM分别是∠ABC,∠ACD,∠PBC,∠PCB的平分线,则∠M的度数为______.
10、如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′,BE,CD交于点F.若∠BAC=40°,则∠BFC的度数为 _____.
三、解答题(共 6 小题)
1、小明在学习中遇到这样一个问题:如图,在△ABC 中,AD 平分∠BAC,点 P 为线段 AD 上的一个动点,PE⊥AD 交 BC 的延长线于点 E.猜想∠B、∠ACB、∠E 的数量关系.
(1)小明阅读题目后,没有发现数量关系与解题思路,于是尝试从具体的情况开始探索,若∠B=35°,∠ACB=85°,则∠E= .
(2)小明继续探究,设∠B=α,∠ACB=β(β>α),当点 P 在线段 AD 上运动时,求∠E 的大小.(用含α、β的代数式表示)
2、在△ABC中,AD是角平分线..
(1)如图(1),AE是高,,,求∠DAE的度数;
(2)如图(2),点E在AD上,于F,试探究∠DEF与∠B、∠C的大小关系,并证明你的结论;
(3)如图(3),点E在AD的延长线上.于F,试探究∠DEF与∠B、∠C的大小关系是___(直接写出结论,不需证明).
3、如图,在△ABC中,∠ABC=40°, ∠ACB=90°,AE平分∠BAC交BC于点E.P是边BC上的动点(不与B,C重合),连结AP,将△APC沿AP翻折得△APD,连结DC,记∠BCD=α.
(1)如图,当P与E重合时,求α的度数.
(2)当P与E不重合时,记∠BAD=β,探究α与β的数量关系.
4、【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【简单应用】
(2)如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=46°,∠ADC=26°,求∠P的度数;
【问题探究】
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
【拓展延伸】
(4) ①在图4中,若设∠C=α,∠B=β,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C、∠B之间的数量关系为: (用α、β表示∠P);
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE, 猜想∠P与∠B、∠D的关系,直接写出结论.
5、小明在学习中遇到这样一个问题:如图1,在△ABC中,∠C>∠B,AE平分∠BAC,AD⊥BC于D.猜想∠B、∠C、∠EAD的数量关系.
(1)小明阅读题目后,没有发现数量关系与解题思路,于是尝试代入∠B、∠C的值求∠EAD值,得到下面几组对应值:
∠B/度 10 30 30 20 20
∠C/度 70 70 60 60 80
∠EAD/度 30 a 15 20 30
上表中a= ,于是得到∠B、∠C、∠EAD的数量关系为 .
(2)小明继续探究,在线段AE上任取一点P,过点P作PD⊥BC于点D,请尝试写出∠B、∠C、∠EPD之间的数量关系,并说明理由.
(3)小明突发奇想,交换B、C两个字母位置,如图2,过EA的延长线是一点F作FD⊥BC交CB的延长线于D,当∠ABC=80°,∠C=24°时,∠F度数为 °.
6、实践与探究
材料:锐角三角形卡纸ABC,正方形卡纸DEFG.
操作一:如图①,将放置在正方形卡纸DEFG上,使点D在内,点B、C分别在边DG和边DE上.
(1)若,则∠ABC+∠ACB=_________°,∠DBC+∠DCB=_________°,∠ABD+∠ACD=_________°.
(2)请你探究∠ABD+∠ACD与∠A之间的数量关系,并说明理由.
操作二:如图②,改变正方形卡纸DEFG的位置,使点D在外,且在AB边的左侧,点B、C分别在边DG和边DE上,则∠ABD、∠ACD与∠A的数量关系为_________
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,中,分别是边上的点,连接,将沿着者折叠,得到,当的三边与的三边有一组边平行时,的度数不可能是( )
A. B. C. D.
2、如图,△ABC中∠A=40°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,点C恰好落在BE上的点G处,此时∠BDC=82°,则原三角形的∠B的度数为( )
A.57° B.60° C.63° D.70°
3、若△ABC三个角的大小满足条件∠A:∠B:∠C=1:3:4,则∠C的大小为( )
A.22.5° B.45° C.67.5° D.90°
4、如图,,,则、和的关系是( )
B.
C. D.
5、如图,把沿线段折叠,使点落在点处;若,,,则的度数为( )
A. B. C. D.
6、如图,在三角形ABC中,,,D是BC上一点,将三角形ABD沿AD翻折后得到三角形AED,边AE交射线BC于点F,若,则( )
A.120° B.135° C.110° D.150°
7、如图,把△ABC沿EF对折,折叠后的图形如图所示,,,则 的度数为( )
A. B. C. D.
8、如图7,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F=135°,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9、如图,的两条角平分线,交于点,若,则为( )
A.112° B.115° C.120° D.125°
10、如图,在△ABC中,∠A=78°,∠EBD=∠EDB,DF平分∠EDC,则∠BDF的度数为( )
A.35° B.39° C.40° D.45°
二、填空题(共 10 小题)
1、如图,______.
2、如图.有一个三角形纸片,,,将纸片一角折叠,使点落在外,若,则的大小为______.
3、如图,在中,,D是边上一点,平分.
(1)若,,的度数为___________;
(2)若,,的度数为__________.(用含m,n的式子表示)
4、如图,将沿翻折,顶点均落在O处,且与重合于线段,测得,则________度.
5、如图,在△ABC,AD 是角平分线,AE 是中线,AF 是高.如果BC=10cm,那么 BE=_____;∠ABC=40°,∠ACB=60°,那么∠DAF=_____°.
6、如图,直线,点、分别在上,.过线段上的点作交于点,则的大小为_____度.
7、如图,在△ABC 中,∠ACB=60°,D 为△ABC 边 AC 上一点,BC=CD,点 M 在 BC 的延长线上, CE 平分∠ACM,且 AC=CE.连接 BE 交 AC 于 F,G 为边 CE 上一点,满足 CG=CF,连接 DG 交 BE 于 H.以下结论:①△ABC≌△EDC; ②∠DHF =60°;③若∠A=60°,则 AB∥CE;④若 BE 平分∠ABC 中,则 EB 平分∠DEC;正确的有_____(只填序号)
8、如图,在四边形ABCD中,∠BCD=50°,∠B=∠D=90°,在BC、CD上分别取一点M、N,使△AMN的周长最小,则∠MAN=_____°.
9、如图所示,△中,,BP,CP,BM,CM分别是∠ABC,∠ACD,∠PBC,∠PCB的平分线,则∠M的度数为______.
10、如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′,BE,CD交于点F.若∠BAC=40°,则∠BFC的度数为 _____.
三、解答题(共 6 小题)
1、小明在学习中遇到这样一个问题:如图,在△ABC 中,AD 平分∠BAC,点 P 为线段 AD 上的一个动点,PE⊥AD 交 BC 的延长线于点 E.猜想∠B、∠ACB、∠E 的数量关系.
(1)小明阅读题目后,没有发现数量关系与解题思路,于是尝试从具体的情况开始探索,若∠B=35°,∠ACB=85°,则∠E= .
(2)小明继续探究,设∠B=α,∠ACB=β(β>α),当点 P 在线段 AD 上运动时,求∠E 的大小.(用含α、β的代数式表示)
2、在△ABC中,AD是角平分线..
(1)如图(1),AE是高,,,求∠DAE的度数;
(2)如图(2),点E在AD上,于F,试探究∠DEF与∠B、∠C的大小关系,并证明你的结论;
(3)如图(3),点E在AD的延长线上.于F,试探究∠DEF与∠B、∠C的大小关系是___(直接写出结论,不需证明).
3、如图,在△ABC中,∠ABC=40°, ∠ACB=90°,AE平分∠BAC交BC于点E.P是边BC上的动点(不与B,C重合),连结AP,将△APC沿AP翻折得△APD,连结DC,记∠BCD=α.
(1)如图,当P与E重合时,求α的度数.
(2)当P与E不重合时,记∠BAD=β,探究α与β的数量关系.
4、【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【简单应用】
(2)如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=46°,∠ADC=26°,求∠P的度数;
【问题探究】
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
【拓展延伸】
(4) ①在图4中,若设∠C=α,∠B=β,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C、∠B之间的数量关系为: (用α、β表示∠P);
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE, 猜想∠P与∠B、∠D的关系,直接写出结论.
5、小明在学习中遇到这样一个问题:如图1,在△ABC中,∠C>∠B,AE平分∠BAC,AD⊥BC于D.猜想∠B、∠C、∠EAD的数量关系.
(1)小明阅读题目后,没有发现数量关系与解题思路,于是尝试代入∠B、∠C的值求∠EAD值,得到下面几组对应值:
∠B/度 10 30 30 20 20
∠C/度 70 70 60 60 80
∠EAD/度 30 a 15 20 30
上表中a= ,于是得到∠B、∠C、∠EAD的数量关系为 .
(2)小明继续探究,在线段AE上任取一点P,过点P作PD⊥BC于点D,请尝试写出∠B、∠C、∠EPD之间的数量关系,并说明理由.
(3)小明突发奇想,交换B、C两个字母位置,如图2,过EA的延长线是一点F作FD⊥BC交CB的延长线于D,当∠ABC=80°,∠C=24°时,∠F度数为 °.
6、实践与探究
材料:锐角三角形卡纸ABC,正方形卡纸DEFG.
操作一:如图①,将放置在正方形卡纸DEFG上,使点D在内,点B、C分别在边DG和边DE上.
(1)若,则∠ABC+∠ACB=_________°,∠DBC+∠DCB=_________°,∠ABD+∠ACD=_________°.
(2)请你探究∠ABD+∠ACD与∠A之间的数量关系,并说明理由.
操作二:如图②,改变正方形卡纸DEFG的位置,使点D在外,且在AB边的左侧,点B、C分别在边DG和边DE上,则∠ABD、∠ACD与∠A的数量关系为_________
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
