湘教版2023-2024学年度上学期八年级期末模拟数学试题2(含解析)
文档属性
| 名称 | 湘教版2023-2024学年度上学期八年级期末模拟数学试题2(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 13:07:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版2023-2024八年级上期末模拟试题2
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
的算术平方根是( )
A. B. C.±2 D.2
计算的结果为( )
A.1 B. C. D.
对于任意三角形的高,下列说法不正确的是( )
A. 锐角三角形有三条高
B. 直角三角形只有一条高
C. 任意三角形都有三条高
D. 钝角三角形有两条高在三角形的外部
如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕点O自由转动,就做成了一个测量工件,则A′B′的长等于内槽宽AB,则判定△OAB≌△OA′B′的理由是( )
A. 边边边 B. 角边角 C. 边角边 D. 角角边
四边形ABCD的边长如图所示,对角线AC的长度随四边形形状的改变而变化.当△ABC为等腰三角形时,对角线AC的长为( )
A.2 B.3 C.4 D.5
不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
下列运算正确的是( )
A. B.
C. D.
学校为了丰富学生的知识,需要购买一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多8元,已知学校用15000元购买科普类图书的本数与用12000元购买文学书的本数相等,设文学类图书平均每本x元,则列方程正确的是( )
A.
C.
如图,BD是∠ABC的角平分线,AD⊥AB,AD=3,BC=5,则△BCD的面积为( )
A.7.5 B.8 C.10 D.15
已知,作的平分线,在射线上截取线段,分别以O、C为圆心,大于的长为半径画弧,两弧相交于E,F.画直线,分别交于D,交于G.那么,一定是( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.直角三角形
1 、填空题(本大题共8小题,每小题3分,共24分)
设n为正整数,若n<<n+1,则n的值为 .
如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是
关于x的方程=﹣1的解是正数,则a的取值范围是 .
不等式组的解集是 .
若计算的结果为正整数,则无理数的值可以是__________.(写出一个符合条件的即可)
等腰三角形的周长为17cm,其中一边长为4cm,则该等腰三角形的腰长为 cm.
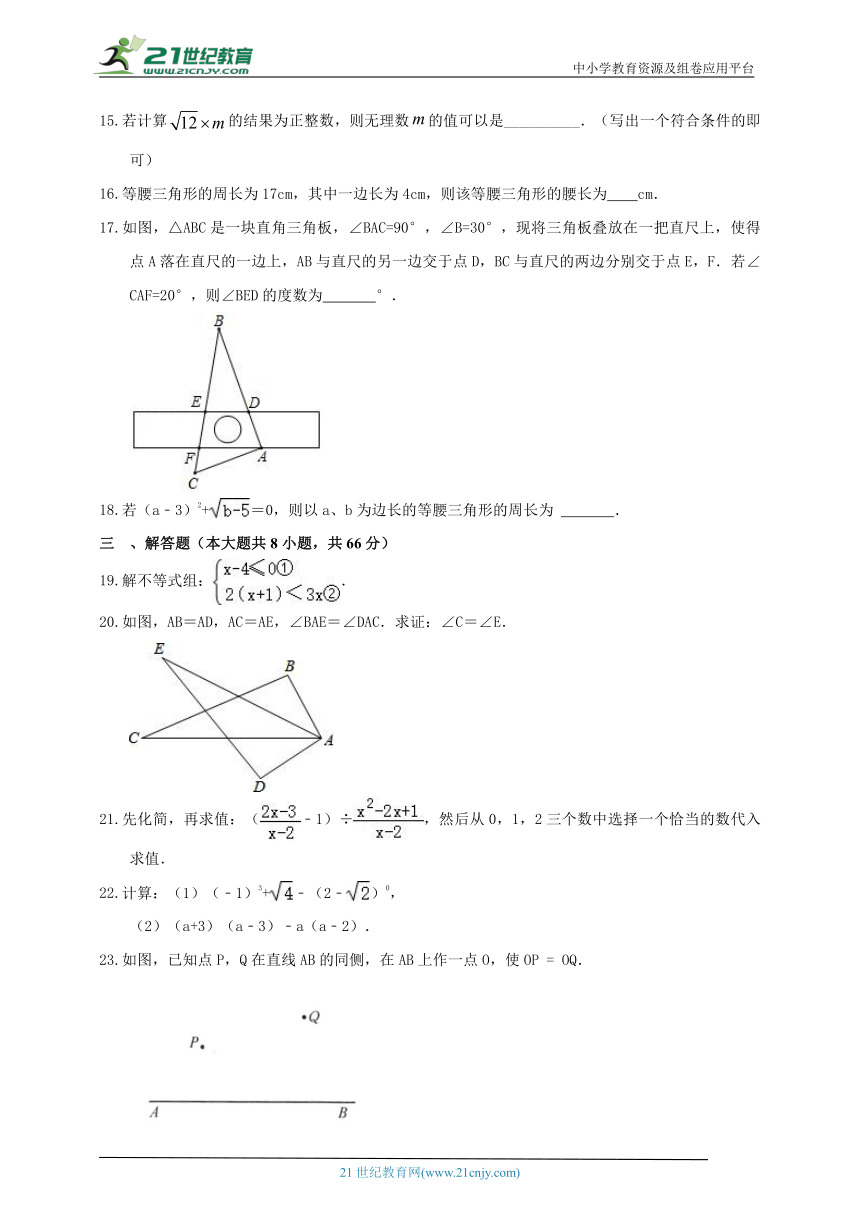
如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°,现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为 °.
若(a﹣3)2+=0,则以a、b为边长的等腰三角形的周长为 .
1 、解答题(本大题共8小题,共66分)
解不等式组:.
如图,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
先化简,再求值:(﹣1)÷,然后从0,1,2三个数中选择一个恰当的数代入求值.
计算:(1)(﹣1)3+﹣(2﹣)0,
(2)(a+3)(a﹣3)﹣a(a﹣2).
如图,已知点P,Q在直线AB的同侧,在AB上作一点O,使OP = OQ.
为了提高广大职工对消防知识的学习热情,增强职工的消防意识,某单位工会决定组织消防知识竞赛活动,本次活动拟设一、二等奖若干名,并购买相应奖品.现有经费1275元用于购买奖品,且经费全部用完,已知一等奖奖品单价与二等奖奖品单价之比为4∶3.当用600元购买一等奖奖品时,共可购买一、二等奖奖品25件.
(1)求一、二等奖奖品的单价;
(2)若购买一等奖奖品的数量不少于4件且不超过10件,则共有哪几种购买方式?
为庆祝伟大的中国共产党成立100周年,发扬红色传统,传承红色精神,某学校举行了主题为“学史明理,学史增信,学史崇德,学史力行”的党史知识竞赛,一共有25道题,满分100分,每一题答对得4分,答错扣1分,不答得0分.
(1)若某参赛同学只有一道题没有作答,最后他的总得分为86分,则该参赛同学一共答对了多少道题?
(2)若规定参赛者每道题都必须作答且总得分大于或等于90分才可以被评为“学党史小达人”,则参赛者至少需答对多少道题才能被评为“学党史小达人”?
问题发现:
如图①,△ABC与△ADE是等边三角形,且点B,D,E在同一直线上,连接CE,求∠BEC的度数,并确定线段BD与CE的数量关系.
拓展探究:
如图②,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,且点B,D,E在同一直线上,AF⊥BE于F,连接CE,求∠BEC的度数,并确定线段AF,BF,CE之间的数量关系.
答案解析
1 、选择题
【考点】算术平方根
【分析】直接利用算术平方根的定义得出即可.
解:=2,2的算术平方根是.
故选:B.
【点评】此题主要考查了算术平方根的定义,利用算术平方根即为正平方根求出是解题关键.
【考点】同分母分式的减法
【分析】直接利用同分母分式的减法法则计算即可.
解:.
故选:A.
【点评】本题考查了同分母分式的减法,熟练掌握运算法则是解题的关键.
【考点】三角形的角平分线、中线和高.
【分析】 根据三角形的高的概念,通过具体作高,发现:任意一个三角形都有三条高,其中锐角三角形的三条高都在三角形的内部;直角三角形有两条高即三角形的两条直角边,一条在内部;钝角三角形有两条高在三角形的外部,一条在内部,据此解答即可.
解:A.锐角三角形有三条高,说法正确,故本选项不符合题意;
B、直角三角形有三条高,说法错误,故本选项符合题意;
C、任意三角形都有三条高,说法正确,故本选项不符合题意;
D、钝角三角形有两条高在三角形的外部,说法正确,故本选项不符合题意;
故选B.
【点评】本题考查了三角形的高:从三角形的一个顶点向它的对边作垂线,垂足与顶点之间的线段叫做三角形的高,注意不同形状的三角形的高的位置.
【考点】全等三角形的应用.
【分析】 因为AA′、BB′的中点O连在一起,因此OA=OA′,OB=OB′,还有对顶角相等,所以用的判定定理是边角边.
解:∵AA′、BB′的中点O连在一起,
∴OA=OA′,OB=OB′,
在△OAB和△OA′B′中,
,
∴△OAB≌△OA′B′(SAS).
所以用的判定定理是边角边.
故选:C.
【点评】本题考查全等三角形的判定定理,关键知道是怎么证明的全等,然后找到用的是哪个判定定理.
【考点】等腰三角形的性质,三角形三边关系.
【分析】分两种情况,由三角形的三边关系定理:三角形两边的和大于第三边,即可解决问题.
解:∵△ABC为等腰三角形,
∴AB=AC或AC=BC,
当AC=BC=4时,AD+CD=AC=4,此时不满足三角形三边关系定理,
当AC=AB=3时.满足三角形三边关系定理,
∴AC=3.
故选:B.
【点评】本题考查等腰三角形的性质,三角形的三边关系定理,关键是掌握三角形的三边关系定理.
【考点】解一元一次不等式,并在数轴上表示不等式的解集
【分析】求出不等式的解集,将解集在数轴上表示出来.
解:∵,
∴,
∴,
解得:,
∴不等式的解集为:,
表示在数轴上如图:
故选B.
【点评】本题主要考查了解一元一次不等式,并在数轴上表示不等式的解集,解题的关键在于能够熟练掌握相关知识进行求解.
【考点】二次根式的混合运算,分母有理化.
【分析】直接利用二次根式的混合运算法则分别计算,进而判断得出答案.
解:A.+无法合并,故此选项不合题意,
B.=5,故此选项不合题意,
C.(3﹣)2=11﹣6,故此选项符合题意,
D.6÷×=9,故此选项不合题意.
故选:C.
【点评】此题主要考查了二次根式的混合运算,正确掌握相关运算法则是解题关键.
【考点】由实际问题抽象出分式方程
【分析】设文学类图书平均每本x元,根据购买的书本数相等即可列出方程.
解:设文学类图书平均每本x元,依题意可得
故选B.
【点评】此题主要考查分式方程的应用,解题的关键是根据题意找到等量关系列方程.
【考点】角平分线的性质.
【分析】作DE⊥BC于E,根据角平分线的性质求出DE的长,根据三角形面积公式计算即可.
解:作DE⊥BC于E,
∵BD是∠ABC的角平分线,AD⊥AB,DE⊥BC,
∴DE=DA=3,
∴△BCD=×BC×DE=7.5,
故选:A.
【点评】本题主要考查了角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
【考点】等腰三角形的判定,作图—基本作图
【分析】根据题意知EF垂直平分OC,由此证明△OMD≌△ONG,即可得到OD=OG得到答案.
解:如图,连接CD、CG,
∵分别以O、C为圆心,大于的长为半径画弧,两弧相交于E,F
∴EF垂直平分OC,
设EF交OC于点N,
∴∠ONE=∠ONF=90°,
∵OM平分,
∴∠NOD=∠NOG,
又∵ON=ON,
∴△OMD≌△ONG,
∴OD=OG,
∴△ODG是等腰三角形,
故选:C.
【点评】此题考查基本作图能力:角平分线的做法及线段垂直平分线的做法,还考查了全等三角形的判定定理及性质定理,由此解答问题,根据题意得到EF垂直平分OC是解题的关键.
1 、填空题
【考点】估算无理数的大小.
【分析】先估算出的范围,再得出选项即可.
解:∵1<<2,
∴n=1,
故答案为:1.
【点评】本题考查了估算无理数的大小,能估算出的大小是解此题的关键.
【考点】角平分线的性质.
【分析】过D作DE⊥AB于E,则DE的长度就是D到AB边的距离.
解:∵AD平分∠CAB,∠ACD=90°,DE⊥AB,
∴DC=DE=2(角平分线性质).
【点评】本题主要考查了角平分线上的点到角的两边的距离相等的性质,熟记性质是解题的关键.
【考点】分式方程的解;解一元一次不等式
【分析】先解分式方程,求出x的值,再根据方程的解是正数,确定a的范围即可.
解:=﹣1,解得x=,
=﹣1的解是正数,
0
a>﹣1,
故答案为:a>﹣1.
【点评】本题考查了分式方程的解,解一元一次不等式,熟练掌握解一元一次不等式,解分式方程是解题的关键
【考点】解一元一次不等式组.
【分析】先求出不等式的解集,再求出不等式解集的公共部分.
解:
解不等式①得:x≤2,
解不等式②得:x>﹣1,
∴不等式组的解集是﹣1<x≤2,
故答案为﹣1<x≤2.
【点评】此题主要考查了一元一次不等式组的解法,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
【考点】二次根式的性质与化简
【分析】根据为12,即可得到一个无理数的值.
解:∵,
∴时的结果为正整数,
故答案为:(答案不唯一).
【点评】本题考查了二次根式,注意是解题的关键.
【考点】等腰三角形的性质;三角形三边关系.
【分析】分别从腰长为4cm或底边长为4cm去分析求解即可求得答案.
解:①若腰长为4cm,则底边长委:17﹣4×2=9cm;
②若底边长为4cm,则腰长为:(17﹣4)=6.5cm;
综上可得:该等腰三角形的腰长为4cm或6.5cm.
故答案为:4或6.5.
【点评】此题考查了等腰三角形的性质.注意掌握分类讨论思想的应用是解此题的关键.
【考点】平行线的性质,三角形外角性质
【分析】依据DE∥AF,可得∠BED=∠BFA,再根据三角形外角性质,即可得到∠BFA=20°+60°=80°,进而得出∠BED=80°.
解:如图所示,∵DE∥AF,
∴∠BED=∠BFA,
又∵∠CAF=20°,∠C=60°,
∴∠BFA=20°+60°=80°,
∴∠BED=80°,
故答案为:80.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,同位角相等.
【考点】等腰三角形的性质,非负数的性质:偶次方,非负数的性质:算术平方根,三角形三边关系.
【分析】先求a,b.再求第三边c即可.
解:∵(a﹣3)2+=0,(a﹣3)2≥0,≥0,
∴a﹣3=0,b﹣5=0,
∴a=3,b=5,
设三角形的第三边为c,
当a=c=3时,三角形的周长=a+b+c=3+5+3=11,
当b=c=5时,三角形的周长=3+5+5=13,
故答案为:11或13.
【点评】本题考查等腰三角形周长计算,求出a,b后确定腰和底是求解本题的关键.
1 、解答题
【考点】解一元一次不等式组.
【分析】按照解一元一次不等式组的步骤,进行计算即可解答.
解:,
解不等式①得:x≤4,
解不等式②得:x>2,
∴原不等式组的解集为:2<x≤4.
【点评】本题考查了解一元一次不等式组,熟练掌握解一元一次不等式组的步骤是解题的关键.
【考点】全等三角形的判定与性质
【分析】由“SAS”可证△ABC≌△ADE,可得∠C=∠E.
证明:∵∠BAE=∠DAC
∴∠BAE+∠CAE=∠DAC+∠CAE
∴∠CAB=∠EAD,且AB=AD,AC=AE
∴△ABC≌△ADE(SAS)
∴∠C=∠E
【点评】本题考查了全等三角形的判定和性质,证明∠CAB=∠EAD是本题的关键.
【考点】分式的化简求值
【分析】先根据分式的混合运算顺序和运算法则化简原式,再选取使分式有意义的x的值代入计算可得.
解:原式=(﹣)÷
=
=,
当x=0时,原式=﹣1.
【点评】本题主要考查分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运算法则.
【考点】平方差公式,零指数幂,二次根式的性质与化简,实数的运算,单项式乘多项式.
【分析】(1)先计算负整数指数幂、二次根式、零指数幂,然后计算加减法,
(2)利用平方差公式和单项式乘多项式计算法则去括号,然后合并同类项.
解:(1)(﹣1)3+﹣(2﹣)0
=﹣1+2﹣1
=0,
(2)(a+3)(a﹣3)﹣a(a﹣2)
=a2﹣32﹣a2+2a
=2a﹣9.
【点评】本题主要考查了平方差公式、二次根式、实数的运算以及零指数幂,运用平方差公式计算时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.
【考点】线段垂直平分线的画法,线段垂直平分线的性质
【分析】根据垂直平分线的性质,作出PQ的垂直平分线,交AB于点O即可.
解:连接PQ,分别以P、Q为圆心,大于PQ的长为半径作弧,两弧分别交于M、N,作直线MN,交AB于点O,根据垂直平分线的性质可得OP=OQ,如图所示,点O即为所求.
【点评】此题考查的是尺规作图和垂直平分线的性质,掌握利用尺规作图作线段的垂直平分线是解题关键.
【考点】分式方程的应用,一元一次不等式组的应用
【分析】(1)设一、二等奖奖品的单价分别是4x,3x,根据等量关系,列出分式方程,即可求解;
(2)设购买一等奖品的数量为m件,则购买二等奖品的数量为件,根据4≤m≤10,且为整数,m为整数,即可得到答案.
解:(1)设一、二等奖奖品的单价分别是4x,3x,
由题意得:,解得:x=15,
经检验:x=15是方程的解,且符合题意,
∴15×4=60(元),15×3=45(元),
答:一、二等奖奖品的单价分别是60元,45元;
(2)设购买一等奖品的数量为m件,则购买二等奖品的数量为件,
∵4≤m≤10,且为整数,m为整数,
∴m=4,7,10,
答:共有3种购买方案,分别是:一等奖品数4件,二等奖品数23件;一等奖品数7件,二等奖品数19件;一等奖品数10件,二等奖品数15件.
【点评】本题主要考查分式方程和不等式组的实际应用,准确找出数量关系,列出分式方程或不等式,是解题的关键.
【考点】一元一次方程的应用,一元一次不等式的应用
【分析】(1)设该参赛同学一共答对了道题,从而可得该参赛同学一共答错了道题,再根据“每一题答对得4分,答错扣1分,不答得0分”、“他的总得分为86分”建立方程,解方程即可得;
(2)设参赛者需答对道题才能被评为“学党史小达人”,从而可得参赛者答错了道题,再根据“总得分大于或等于90分”建立不等式,解不等式即可得.
解:(1)设该参赛同学一共答对了道题,则该参赛同学一共答错了道题,
由题意得:,
解得,
答:该参赛同学一共答对了22道题;
(2)设参赛者需答对道题才能被评为“学党史小达人”,则参赛者答错了道题,
由题意得:,
解得,
答:参赛者至少需答对23道题才能被评为“学党史小达人”.
【点评】本题考查了一元一次方程和一元一次不等式的实际应用,正确列出方程和不等式是解题关键.
【考点】全等三角形的判定与性质;等边三角形的性质;等腰直角三角形.
【分析】(1)首先根据△ACB和△DAE均为等边三角形,可得AB=AC,AD=AE,∠BAC=∠DAE=60°,∠ADE=∠AED=60°,据此判断出∠BAD=∠CAE,然后根据全等三角形的判定方法,判断出△ABD≌△ACE,即可判断出BD=CE,∠BDA=∠CEA,进而判断出∠BEC的度数为60°即可;
(2)首先根据△ACB和△DAE均为等腰直角三角形,可得AB=AC,AD=AE,∠BAC=∠DAE=90°,∠ADE=∠AED=45°,据此判断出∠BAD=∠CAE,然后根据全等三角形的判定方法,判断出△ABD≌△ACE,即可判断出BD=CE,∠ADB=∠AEC,进而判断出∠BEC的度数为90°即可;最后根据∠DAE=90°,AD=AE,AF⊥DE,
得到AF=DF=EF,于是得到结论.
解:(1)∵△ACB和△ADE均为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∠ADE=∠AED=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△ACE,
∴BD=CE,∠BDA=∠CEA,
∵点B,D,E在同一直线上,
∴∠ADB=180﹣60=120°,
∴∠AEC=120°,
∴∠BEC=∠AEC﹣∠AED=120﹣60=60°,
综上,可得∠AEB的度数为60°;线段BE与AD之间的数量关系是:BE=AD.
(2)∵△ACB和△DAE均为等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,∠ADE=∠AED=45°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,,
∴△ABD≌△ACE,
∴BD=CE,∠ADB=∠AEC,
∵点A,D,E在同一直线上,
∴∠ADB=180﹣45=135°,
∴∠AEC=135°,
∴∠BEC=∠AEC﹣∠AED=135﹣45=90°;
∵∠DAE=90°,AD=AE,AF⊥DE,
∴AF=DF=EF,
∴DE=DF+EF=2AF,
∴BF=BD+DF=CE+AF.
【点评】此题主要考查了全等三角形的判定方法和性质,要熟练掌握,解答此题的关键是要明确:在判定三角形全等时,关键是选择恰当的判定条件;
此题还考查了等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版2023-2024八年级上期末模拟试题2
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
的算术平方根是( )
A. B. C.±2 D.2
计算的结果为( )
A.1 B. C. D.
对于任意三角形的高,下列说法不正确的是( )
A. 锐角三角形有三条高
B. 直角三角形只有一条高
C. 任意三角形都有三条高
D. 钝角三角形有两条高在三角形的外部
如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕点O自由转动,就做成了一个测量工件,则A′B′的长等于内槽宽AB,则判定△OAB≌△OA′B′的理由是( )
A. 边边边 B. 角边角 C. 边角边 D. 角角边
四边形ABCD的边长如图所示,对角线AC的长度随四边形形状的改变而变化.当△ABC为等腰三角形时,对角线AC的长为( )
A.2 B.3 C.4 D.5
不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
下列运算正确的是( )
A. B.
C. D.
学校为了丰富学生的知识,需要购买一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多8元,已知学校用15000元购买科普类图书的本数与用12000元购买文学书的本数相等,设文学类图书平均每本x元,则列方程正确的是( )
A.
C.
如图,BD是∠ABC的角平分线,AD⊥AB,AD=3,BC=5,则△BCD的面积为( )
A.7.5 B.8 C.10 D.15
已知,作的平分线,在射线上截取线段,分别以O、C为圆心,大于的长为半径画弧,两弧相交于E,F.画直线,分别交于D,交于G.那么,一定是( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.直角三角形
1 、填空题(本大题共8小题,每小题3分,共24分)
设n为正整数,若n<<n+1,则n的值为 .
如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是
关于x的方程=﹣1的解是正数,则a的取值范围是 .
不等式组的解集是 .
若计算的结果为正整数,则无理数的值可以是__________.(写出一个符合条件的即可)
等腰三角形的周长为17cm,其中一边长为4cm,则该等腰三角形的腰长为 cm.
如图,△ABC是一块直角三角板,∠BAC=90°,∠B=30°,现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若∠CAF=20°,则∠BED的度数为 °.
若(a﹣3)2+=0,则以a、b为边长的等腰三角形的周长为 .
1 、解答题(本大题共8小题,共66分)
解不等式组:.
如图,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
先化简,再求值:(﹣1)÷,然后从0,1,2三个数中选择一个恰当的数代入求值.
计算:(1)(﹣1)3+﹣(2﹣)0,
(2)(a+3)(a﹣3)﹣a(a﹣2).
如图,已知点P,Q在直线AB的同侧,在AB上作一点O,使OP = OQ.
为了提高广大职工对消防知识的学习热情,增强职工的消防意识,某单位工会决定组织消防知识竞赛活动,本次活动拟设一、二等奖若干名,并购买相应奖品.现有经费1275元用于购买奖品,且经费全部用完,已知一等奖奖品单价与二等奖奖品单价之比为4∶3.当用600元购买一等奖奖品时,共可购买一、二等奖奖品25件.
(1)求一、二等奖奖品的单价;
(2)若购买一等奖奖品的数量不少于4件且不超过10件,则共有哪几种购买方式?
为庆祝伟大的中国共产党成立100周年,发扬红色传统,传承红色精神,某学校举行了主题为“学史明理,学史增信,学史崇德,学史力行”的党史知识竞赛,一共有25道题,满分100分,每一题答对得4分,答错扣1分,不答得0分.
(1)若某参赛同学只有一道题没有作答,最后他的总得分为86分,则该参赛同学一共答对了多少道题?
(2)若规定参赛者每道题都必须作答且总得分大于或等于90分才可以被评为“学党史小达人”,则参赛者至少需答对多少道题才能被评为“学党史小达人”?
问题发现:
如图①,△ABC与△ADE是等边三角形,且点B,D,E在同一直线上,连接CE,求∠BEC的度数,并确定线段BD与CE的数量关系.
拓展探究:
如图②,△ABC与△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,且点B,D,E在同一直线上,AF⊥BE于F,连接CE,求∠BEC的度数,并确定线段AF,BF,CE之间的数量关系.
答案解析
1 、选择题
【考点】算术平方根
【分析】直接利用算术平方根的定义得出即可.
解:=2,2的算术平方根是.
故选:B.
【点评】此题主要考查了算术平方根的定义,利用算术平方根即为正平方根求出是解题关键.
【考点】同分母分式的减法
【分析】直接利用同分母分式的减法法则计算即可.
解:.
故选:A.
【点评】本题考查了同分母分式的减法,熟练掌握运算法则是解题的关键.
【考点】三角形的角平分线、中线和高.
【分析】 根据三角形的高的概念,通过具体作高,发现:任意一个三角形都有三条高,其中锐角三角形的三条高都在三角形的内部;直角三角形有两条高即三角形的两条直角边,一条在内部;钝角三角形有两条高在三角形的外部,一条在内部,据此解答即可.
解:A.锐角三角形有三条高,说法正确,故本选项不符合题意;
B、直角三角形有三条高,说法错误,故本选项符合题意;
C、任意三角形都有三条高,说法正确,故本选项不符合题意;
D、钝角三角形有两条高在三角形的外部,说法正确,故本选项不符合题意;
故选B.
【点评】本题考查了三角形的高:从三角形的一个顶点向它的对边作垂线,垂足与顶点之间的线段叫做三角形的高,注意不同形状的三角形的高的位置.
【考点】全等三角形的应用.
【分析】 因为AA′、BB′的中点O连在一起,因此OA=OA′,OB=OB′,还有对顶角相等,所以用的判定定理是边角边.
解:∵AA′、BB′的中点O连在一起,
∴OA=OA′,OB=OB′,
在△OAB和△OA′B′中,
,
∴△OAB≌△OA′B′(SAS).
所以用的判定定理是边角边.
故选:C.
【点评】本题考查全等三角形的判定定理,关键知道是怎么证明的全等,然后找到用的是哪个判定定理.
【考点】等腰三角形的性质,三角形三边关系.
【分析】分两种情况,由三角形的三边关系定理:三角形两边的和大于第三边,即可解决问题.
解:∵△ABC为等腰三角形,
∴AB=AC或AC=BC,
当AC=BC=4时,AD+CD=AC=4,此时不满足三角形三边关系定理,
当AC=AB=3时.满足三角形三边关系定理,
∴AC=3.
故选:B.
【点评】本题考查等腰三角形的性质,三角形的三边关系定理,关键是掌握三角形的三边关系定理.
【考点】解一元一次不等式,并在数轴上表示不等式的解集
【分析】求出不等式的解集,将解集在数轴上表示出来.
解:∵,
∴,
∴,
解得:,
∴不等式的解集为:,
表示在数轴上如图:
故选B.
【点评】本题主要考查了解一元一次不等式,并在数轴上表示不等式的解集,解题的关键在于能够熟练掌握相关知识进行求解.
【考点】二次根式的混合运算,分母有理化.
【分析】直接利用二次根式的混合运算法则分别计算,进而判断得出答案.
解:A.+无法合并,故此选项不合题意,
B.=5,故此选项不合题意,
C.(3﹣)2=11﹣6,故此选项符合题意,
D.6÷×=9,故此选项不合题意.
故选:C.
【点评】此题主要考查了二次根式的混合运算,正确掌握相关运算法则是解题关键.
【考点】由实际问题抽象出分式方程
【分析】设文学类图书平均每本x元,根据购买的书本数相等即可列出方程.
解:设文学类图书平均每本x元,依题意可得
故选B.
【点评】此题主要考查分式方程的应用,解题的关键是根据题意找到等量关系列方程.
【考点】角平分线的性质.
【分析】作DE⊥BC于E,根据角平分线的性质求出DE的长,根据三角形面积公式计算即可.
解:作DE⊥BC于E,
∵BD是∠ABC的角平分线,AD⊥AB,DE⊥BC,
∴DE=DA=3,
∴△BCD=×BC×DE=7.5,
故选:A.
【点评】本题主要考查了角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.
【考点】等腰三角形的判定,作图—基本作图
【分析】根据题意知EF垂直平分OC,由此证明△OMD≌△ONG,即可得到OD=OG得到答案.
解:如图,连接CD、CG,
∵分别以O、C为圆心,大于的长为半径画弧,两弧相交于E,F
∴EF垂直平分OC,
设EF交OC于点N,
∴∠ONE=∠ONF=90°,
∵OM平分,
∴∠NOD=∠NOG,
又∵ON=ON,
∴△OMD≌△ONG,
∴OD=OG,
∴△ODG是等腰三角形,
故选:C.
【点评】此题考查基本作图能力:角平分线的做法及线段垂直平分线的做法,还考查了全等三角形的判定定理及性质定理,由此解答问题,根据题意得到EF垂直平分OC是解题的关键.
1 、填空题
【考点】估算无理数的大小.
【分析】先估算出的范围,再得出选项即可.
解:∵1<<2,
∴n=1,
故答案为:1.
【点评】本题考查了估算无理数的大小,能估算出的大小是解此题的关键.
【考点】角平分线的性质.
【分析】过D作DE⊥AB于E,则DE的长度就是D到AB边的距离.
解:∵AD平分∠CAB,∠ACD=90°,DE⊥AB,
∴DC=DE=2(角平分线性质).
【点评】本题主要考查了角平分线上的点到角的两边的距离相等的性质,熟记性质是解题的关键.
【考点】分式方程的解;解一元一次不等式
【分析】先解分式方程,求出x的值,再根据方程的解是正数,确定a的范围即可.
解:=﹣1,解得x=,
=﹣1的解是正数,
0
a>﹣1,
故答案为:a>﹣1.
【点评】本题考查了分式方程的解,解一元一次不等式,熟练掌握解一元一次不等式,解分式方程是解题的关键
【考点】解一元一次不等式组.
【分析】先求出不等式的解集,再求出不等式解集的公共部分.
解:
解不等式①得:x≤2,
解不等式②得:x>﹣1,
∴不等式组的解集是﹣1<x≤2,
故答案为﹣1<x≤2.
【点评】此题主要考查了一元一次不等式组的解法,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
【考点】二次根式的性质与化简
【分析】根据为12,即可得到一个无理数的值.
解:∵,
∴时的结果为正整数,
故答案为:(答案不唯一).
【点评】本题考查了二次根式,注意是解题的关键.
【考点】等腰三角形的性质;三角形三边关系.
【分析】分别从腰长为4cm或底边长为4cm去分析求解即可求得答案.
解:①若腰长为4cm,则底边长委:17﹣4×2=9cm;
②若底边长为4cm,则腰长为:(17﹣4)=6.5cm;
综上可得:该等腰三角形的腰长为4cm或6.5cm.
故答案为:4或6.5.
【点评】此题考查了等腰三角形的性质.注意掌握分类讨论思想的应用是解此题的关键.
【考点】平行线的性质,三角形外角性质
【分析】依据DE∥AF,可得∠BED=∠BFA,再根据三角形外角性质,即可得到∠BFA=20°+60°=80°,进而得出∠BED=80°.
解:如图所示,∵DE∥AF,
∴∠BED=∠BFA,
又∵∠CAF=20°,∠C=60°,
∴∠BFA=20°+60°=80°,
∴∠BED=80°,
故答案为:80.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,同位角相等.
【考点】等腰三角形的性质,非负数的性质:偶次方,非负数的性质:算术平方根,三角形三边关系.
【分析】先求a,b.再求第三边c即可.
解:∵(a﹣3)2+=0,(a﹣3)2≥0,≥0,
∴a﹣3=0,b﹣5=0,
∴a=3,b=5,
设三角形的第三边为c,
当a=c=3时,三角形的周长=a+b+c=3+5+3=11,
当b=c=5时,三角形的周长=3+5+5=13,
故答案为:11或13.
【点评】本题考查等腰三角形周长计算,求出a,b后确定腰和底是求解本题的关键.
1 、解答题
【考点】解一元一次不等式组.
【分析】按照解一元一次不等式组的步骤,进行计算即可解答.
解:,
解不等式①得:x≤4,
解不等式②得:x>2,
∴原不等式组的解集为:2<x≤4.
【点评】本题考查了解一元一次不等式组,熟练掌握解一元一次不等式组的步骤是解题的关键.
【考点】全等三角形的判定与性质
【分析】由“SAS”可证△ABC≌△ADE,可得∠C=∠E.
证明:∵∠BAE=∠DAC
∴∠BAE+∠CAE=∠DAC+∠CAE
∴∠CAB=∠EAD,且AB=AD,AC=AE
∴△ABC≌△ADE(SAS)
∴∠C=∠E
【点评】本题考查了全等三角形的判定和性质,证明∠CAB=∠EAD是本题的关键.
【考点】分式的化简求值
【分析】先根据分式的混合运算顺序和运算法则化简原式,再选取使分式有意义的x的值代入计算可得.
解:原式=(﹣)÷
=
=,
当x=0时,原式=﹣1.
【点评】本题主要考查分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运算法则.
【考点】平方差公式,零指数幂,二次根式的性质与化简,实数的运算,单项式乘多项式.
【分析】(1)先计算负整数指数幂、二次根式、零指数幂,然后计算加减法,
(2)利用平方差公式和单项式乘多项式计算法则去括号,然后合并同类项.
解:(1)(﹣1)3+﹣(2﹣)0
=﹣1+2﹣1
=0,
(2)(a+3)(a﹣3)﹣a(a﹣2)
=a2﹣32﹣a2+2a
=2a﹣9.
【点评】本题主要考查了平方差公式、二次根式、实数的运算以及零指数幂,运用平方差公式计算时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.
【考点】线段垂直平分线的画法,线段垂直平分线的性质
【分析】根据垂直平分线的性质,作出PQ的垂直平分线,交AB于点O即可.
解:连接PQ,分别以P、Q为圆心,大于PQ的长为半径作弧,两弧分别交于M、N,作直线MN,交AB于点O,根据垂直平分线的性质可得OP=OQ,如图所示,点O即为所求.
【点评】此题考查的是尺规作图和垂直平分线的性质,掌握利用尺规作图作线段的垂直平分线是解题关键.
【考点】分式方程的应用,一元一次不等式组的应用
【分析】(1)设一、二等奖奖品的单价分别是4x,3x,根据等量关系,列出分式方程,即可求解;
(2)设购买一等奖品的数量为m件,则购买二等奖品的数量为件,根据4≤m≤10,且为整数,m为整数,即可得到答案.
解:(1)设一、二等奖奖品的单价分别是4x,3x,
由题意得:,解得:x=15,
经检验:x=15是方程的解,且符合题意,
∴15×4=60(元),15×3=45(元),
答:一、二等奖奖品的单价分别是60元,45元;
(2)设购买一等奖品的数量为m件,则购买二等奖品的数量为件,
∵4≤m≤10,且为整数,m为整数,
∴m=4,7,10,
答:共有3种购买方案,分别是:一等奖品数4件,二等奖品数23件;一等奖品数7件,二等奖品数19件;一等奖品数10件,二等奖品数15件.
【点评】本题主要考查分式方程和不等式组的实际应用,准确找出数量关系,列出分式方程或不等式,是解题的关键.
【考点】一元一次方程的应用,一元一次不等式的应用
【分析】(1)设该参赛同学一共答对了道题,从而可得该参赛同学一共答错了道题,再根据“每一题答对得4分,答错扣1分,不答得0分”、“他的总得分为86分”建立方程,解方程即可得;
(2)设参赛者需答对道题才能被评为“学党史小达人”,从而可得参赛者答错了道题,再根据“总得分大于或等于90分”建立不等式,解不等式即可得.
解:(1)设该参赛同学一共答对了道题,则该参赛同学一共答错了道题,
由题意得:,
解得,
答:该参赛同学一共答对了22道题;
(2)设参赛者需答对道题才能被评为“学党史小达人”,则参赛者答错了道题,
由题意得:,
解得,
答:参赛者至少需答对23道题才能被评为“学党史小达人”.
【点评】本题考查了一元一次方程和一元一次不等式的实际应用,正确列出方程和不等式是解题关键.
【考点】全等三角形的判定与性质;等边三角形的性质;等腰直角三角形.
【分析】(1)首先根据△ACB和△DAE均为等边三角形,可得AB=AC,AD=AE,∠BAC=∠DAE=60°,∠ADE=∠AED=60°,据此判断出∠BAD=∠CAE,然后根据全等三角形的判定方法,判断出△ABD≌△ACE,即可判断出BD=CE,∠BDA=∠CEA,进而判断出∠BEC的度数为60°即可;
(2)首先根据△ACB和△DAE均为等腰直角三角形,可得AB=AC,AD=AE,∠BAC=∠DAE=90°,∠ADE=∠AED=45°,据此判断出∠BAD=∠CAE,然后根据全等三角形的判定方法,判断出△ABD≌△ACE,即可判断出BD=CE,∠ADB=∠AEC,进而判断出∠BEC的度数为90°即可;最后根据∠DAE=90°,AD=AE,AF⊥DE,
得到AF=DF=EF,于是得到结论.
解:(1)∵△ACB和△ADE均为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,∠ADE=∠AED=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△ACE,
∴BD=CE,∠BDA=∠CEA,
∵点B,D,E在同一直线上,
∴∠ADB=180﹣60=120°,
∴∠AEC=120°,
∴∠BEC=∠AEC﹣∠AED=120﹣60=60°,
综上,可得∠AEB的度数为60°;线段BE与AD之间的数量关系是:BE=AD.
(2)∵△ACB和△DAE均为等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,∠ADE=∠AED=45°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD和△ACE中,,
∴△ABD≌△ACE,
∴BD=CE,∠ADB=∠AEC,
∵点A,D,E在同一直线上,
∴∠ADB=180﹣45=135°,
∴∠AEC=135°,
∴∠BEC=∠AEC﹣∠AED=135﹣45=90°;
∵∠DAE=90°,AD=AE,AF⊥DE,
∴AF=DF=EF,
∴DE=DF+EF=2AF,
∴BF=BD+DF=CE+AF.
【点评】此题主要考查了全等三角形的判定方法和性质,要熟练掌握,解答此题的关键是要明确:在判定三角形全等时,关键是选择恰当的判定条件;
此题还考查了等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
