湘教版2023-2024学年度上学期八年级期末模拟数学试题1(含解析)
文档属性
| 名称 | 湘教版2023-2024学年度上学期八年级期末模拟数学试题1(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教版2023-2024八年级上期末模拟试题1
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共10小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
下列结论正确的是( )
A.形状相同的两个图形是全等形
B.对应角相等的两个三角形是全等三角形
C.全等三角形的面积相等
D.两个等边三角形全等
计算,结果正确的是( )
A.1 B.x C. D.
如图,在△ABC中,D,E分别为BC上两点,且BD=DE=EC,则图中面积相等的三角形有( )对.
A. 4 B. 5 C. 6 D. 7
如图,在 Rt△ABC 中,∠C=90°,∠A=30°,若AB=8,则BC 等于 ( )
A.4 B.3 C.2 D.1
下列各数中比3大比4小的无理数是( )
A. B. C.3.1 D.
如图,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还添加一个条件才能使△ABC≌△DEF,下列不能添加的条件是( )
A.∠B=∠E B.BC=EF C.∠C=∠F D.AC=DF
如图,在△ABC中,∠A=50°,AD为∠A的平分线,DE⊥AB,DF⊥AC,则∠DEF=( )
A.15° B.25° C.35° D.20°
《九章算术》中记录的一道题目译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马速度的2倍,求规定时间.设规定时间为x天,所列方程正确的是( )
A.×2= B.=×2 C.×2= D.=×2
(﹣2)2008(+2)2007的值等于( )
A.2 B.﹣2 C. D.
如果不等式无解,则b的取值范围是( )
A.b>﹣2 B.b<﹣2 C.b≥﹣2 D.b≤﹣2
1 、填空题(本大题共8小题,每小题3分,共18分)
8的立方根等于 .
如图,∠A+∠B+∠C+∠D+∠E的度数为 度.
化简:(+) = .
数式的最大值为 ,此时x= .
如图,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹.
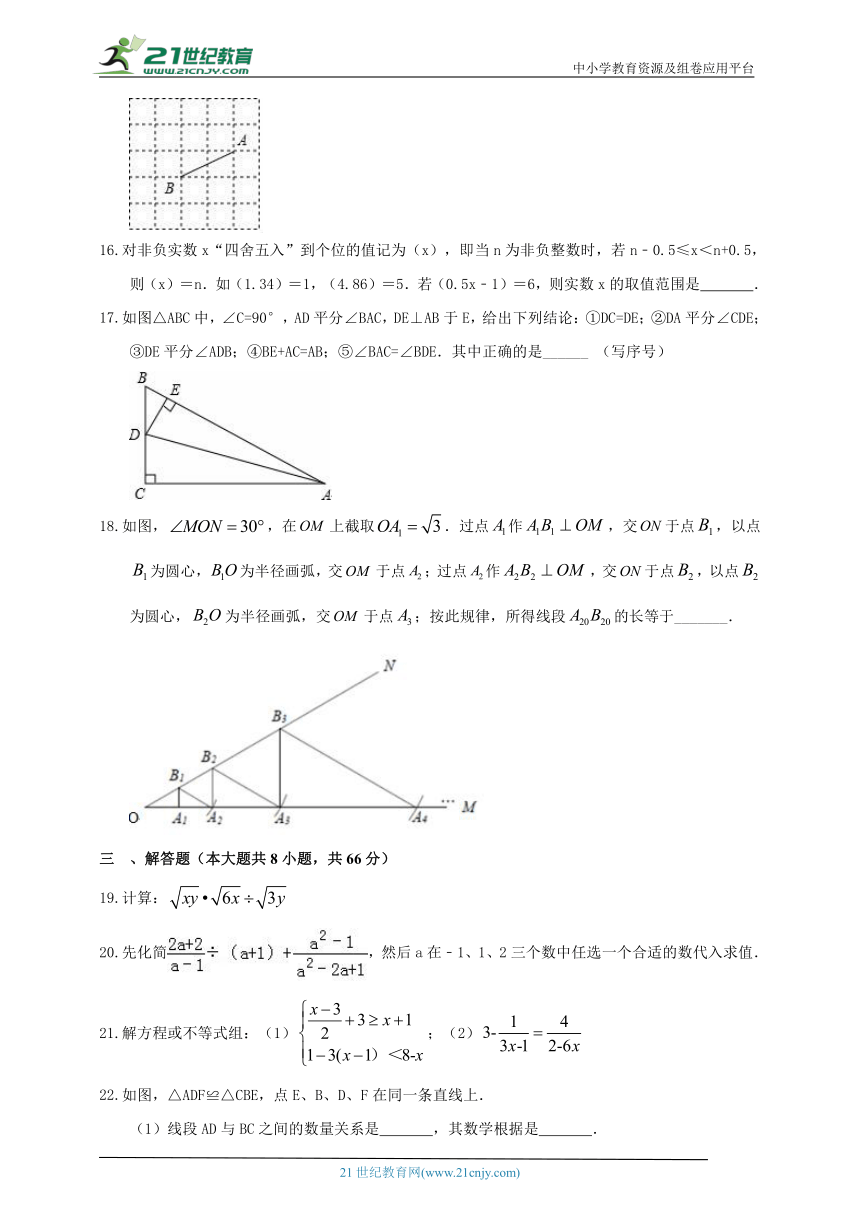
对非负实数x“四舍五入”到个位的值记为(x),即当n为非负整数时,若n﹣0.5≤x<n+0.5,则(x)=n.如(1.34)=1,(4.86)=5.若(0.5x﹣1)=6,则实数x的取值范围是 .
如图△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,给出下列结论:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正确的是______ (写序号)
如图,,在上截取.过点作,交于点,以点为圆心,为半径画弧,交于点;过点作,交于点,以点为圆心,为半径画弧,交于点;按此规律,所得线段的长等于_______.
1 、解答题(本大题共8小题,共66分)
计算:
先化简,然后a在﹣1、1、2三个数中任选一个合适的数代入求值.
解方程或不等式组:(1);(2)
如图,△ADF≌△CBE,点E、B、D、F在同一条直线上.
(1)线段AD与BC之间的数量关系是 ,其数学根据是 .
(2)判断AD与BC之间的位置关系,并说明理由.
小明和小莉在跑道上进行100m短跑比赛,两人从出发点同时起跑,小明到达终点时,小莉离终点还差6m,已知小明和小莉的平均速度分别为x m/s、y m/s.
(1)如果两人重新开始比赛,小明从起点向后退6m,两人同时起跑能否同时到达终点?若能,请求出两人到达终点的时间;若不能,请说明谁先到达终点.
(2)如果两人想同时到达终点,应如何安排两人起跑位置?请设计两种方案.
如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A.F的直线垂直平分线段BC.
现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂在A.B两种不同规格的货车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元.
(1)设运送这批货物的总费用为y万元,这列货车挂A型车厢x节,试定出用车厢节数x表示总费用y的公式.
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A.B两种车厢的节数,那么共有哪几种安排车厢的方案?
△ABC和△ADE都是等边三角形.
(1)将△ADE绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有PA+PB=PC(或PA+PC=PB)成立(不需证明),
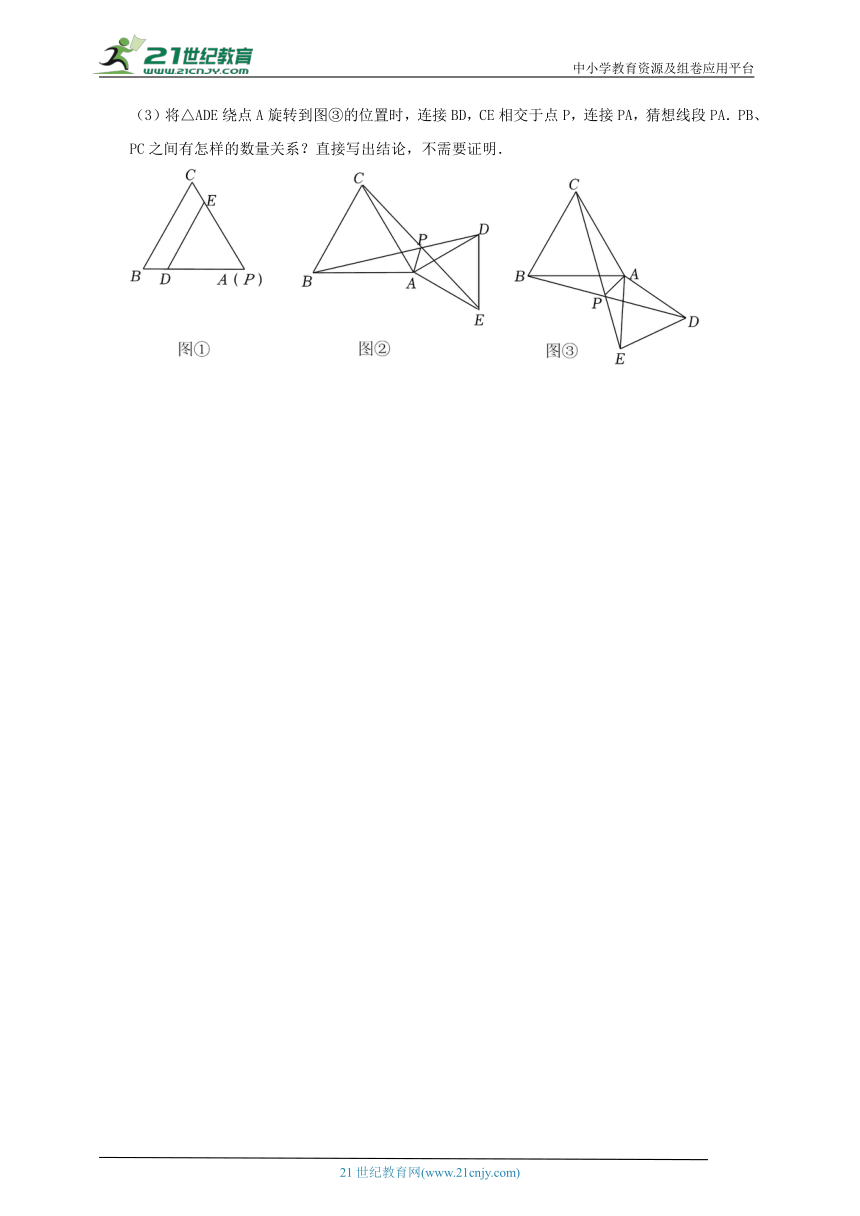
(2)将△ADE绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA.PB、PC之间有怎样的数量关系?并加以证明,
(3)将△ADE绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA.PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.
答案解析
1 、选择题
【考点】全等图形的定义与性质
【分析】根据全等图形的定义对各选项分析判断后利用排除法求解.
解:A.应为形状相同,大小相等的两个图形是全等形,故本选项错误;
B、应为对应角相等,对应边相等的两个三角形是全等三角形,故本选项错误;
C、全等三角形的面积相等,正确,故本选项正确;
D、应为两个边长相等的等边三角形全等,故本选项错误.
故选C.
【点评】本题考查了全等图形的定义,以及全等三角形的性质,要注意从形状和大小两个方面考虑求解.
【考点】分式的加减法
【分析】根据分式的运算法则即可求出答案.
解:原式=
=1
故选:A.
【点评】本题考查分式的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.
【考点】三角形的角平分线、中线和高
【分析】根据三角形的面积公式,知:只要同底等高,则两个三角形的面积相等,据此可得面积相等的三角形.
解:由已知条件,得△ABD,△ADE,△ACE,3个三角形的面积都相等,组成了3对,
还有△ABE和△ACD的面积相等,共4对.
故选A.
【点评】本题考查了三角形的相关知识,解题的关键是熟练的掌握三角形面积公式与运用.
【考点】含30度角的直角三角形
【分析】根据含30度角的直角三角形的性质解答即可
解:根据含30度角的直角三角形的性质可知:BC=AB=4cm.
故选A
【点评】本题考查了含30度角的直角三角形,记住含30度角的直角三角形的性质是解题的关键.
【考点】算术平方根,无理数,实数大小比较
【分析】由于带根号的要开不尽方是无理数,无限不循环小数为无理数,根据无理数的定义即可求解.
解:∵四个选项中是无理数的只有和,而>4,3<<4
∴选项中比3大比4小的无理数只有.
故选:A.
【点评】此题主要考查了无理数的定义,解题时注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.
【考点】全等三角形的判定.
【分析】利用判定两个三角形全等的方法SSS、SAS、ASA.AAS、HL进行分析.
解:A.添加∠B=∠E,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
B、添加BC=EF,不能判定△ABC≌△DEF,故此选项符合题意;
C、添加∠C=∠F,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
D、添加AC=DF,可利用SAS定理判定△ABC≌△DEF,故此选项不合题意;
故选:B.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA.AAS、HL.
注意:AAA.SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
【考点】角平分线的性质;等腰三角形的判定与性质.
【分析】根据角平分线性质得出DE=DF,求出∠AAED=∠AFD=90°,求出∠EDF,根据等腰三角形性质和三角形的内角和定理求出即可.
解:∵AD为∠A的平分线,DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,DE=DF,
∵∠EDF=360°﹣∠AED﹣∠AFD﹣∠BAC=360°﹣90°﹣90°﹣50°=130°,
∵DE=DF,
∴∠DEF=∠DFE=(180°﹣∠EDF)=×(180°﹣130°)=25°,
故选B.
【点评】本题考查了等腰三角形性质,多边形的内角和定理,等腰三角形的性质的应用,注意:角平分线上的点到角两边的距离相等.
【考点】由实际问题抽象出分式方程,数学常识.
【分析】根据用快、慢马送所需时间与规定时间之间的关系,可得出用慢马送需要(x+1)天,用快马送需要(x﹣3)天,利用速度=路程÷时间,结合快马的速度是慢马速度的2倍,即可列出关于x的分式方程,此题得解.
解:∵用慢马送,需要的时间比规定时间多一天,用快马送,所需的时间比规定时间少3天,且规定时间为x天,
∴用慢马送需要(x+1)天,用快马送需要(x﹣3)天.
根据题意得:×2=.
故选:A.
【点评】本题考查了由实际问题抽象出分式方程以及数学常识,找准等量关系,正确列出分式方程是解题的关键.
【考点】二次根式的乘除法
【分析】根据am bm=(ab)m,先把原式化简后再求值.
解:原式=(﹣2)(﹣2)2007(+2)2007
=(﹣2)×(﹣1)=2﹣.
故选D.
【点评】正确理解二次根式乘法、积的乘方法则是解答问题的关键.
【考点】解一元一次不等式组.
【分析】不等式组无解就是两个不等式的解集没有公共部分,可利用数轴进行求解.
解:x>﹣2在数轴上表示点﹣2右边的部分,x<b表示点b左边的部分.
当点b在﹣2这点或这点的左边时,两个不等式没有公共部分,即不等式组无解,
则b≤﹣2.
故选D.
【点评】本题考查不等式组中不等式的未知字母的取值,利用数轴能直观的得到,易于理解.
1 、填空题
【考点】立方根
【分析】根据立方根的定义得出,求出即可.
解:8的立方根是=2,
故答案为:2.
【点评】本题考查了对立方根的应用,注意:a的立方根是,其中a可以为正数、负数和0.
【考点】三角形的外角性质;三角形内角和定理.
【分析】如图连接CE,根据三角形的一个外角等于和它不相邻的两个内角和∠1=∠A+∠B=∠2+∠3,在△DCE中有∠D+∠2+∠DCB+∠3+∠AED=180°,即可得∠D+∠A+∠DCB+∠B+∠AED=180°.
解:如图连接CE,
根据三角形的外角性质得∠1=∠A+∠B=∠2+∠3,
在△DCE中有,∠D+∠2+∠DCB+∠3+∠AED=180°,
∴∠D+∠A+∠DCB+∠B+∠AED=180°.
【点评】 本题运用三角形的一个外角等于和它不相邻的两个内角和,将已知角转化在同一个三角形中,再根据三角形内角和定理求解.
【考点】分式的混合运算.
【分析】首先计算括号內的加法,然后计算乘法即可化简.
解:原式=(﹣)
=
=1.
故答案为1.
【考点】二次根式的定义
【分析】根据算术平方根的性质可以得到≥0,即最小值是0,据此即可确定原式的最大值.
解:≥0,
∴当x=±2时,有最小值0,
则当x=±2,3-有最大值是3.
故答案是:3,±2.
【点评】本题考查了二次根式性质,理解≥0是关键.
【考点】 作图—应用与设计作图; 线段垂直平分线的性质.
【分析】以AB为边作正方形ABCD,正方形ABEF,连接AC,BD交于O,连接AE,BF交于O′,过O,O′作直线OO′于是得到结论.
解:如图所示,直线OO′即为所求.
【点评】本题考查了作图-应用与设计作图,正方形的性质,线段的垂直平分线的性质,正确的作出图形是解题的关键.
【考点】一元一次不等式组的应用
【分析】根据题意得到:6﹣0.5≤0.5x﹣1<6+0.5,据此求得x的取值范围.
解:依题意得:6﹣0.5≤0.5x﹣1<6+0.5
解得13≤x<15.
故答案是:13≤x<15.
【点评】考查了一元一次不等式组的应用,解题的关键是得到关于x的不等式组6﹣0.5≤0.5x﹣1<6+0.5.
【考点】角平分线的性质;全等三角形的判定与性质
【分析】根据角平分线上的点到角的两边的距离相等可得DC=DE,判断①正确,然后利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应角相等可得∠ADC=∠ADE,判断②正确;全等三角形对应边相等可得AC=AE,然后求出BE+AC=AB,判断④正确;根据同角的余角相等求出∠BAC=∠BDE,判断⑤正确,并得到③错误.
解:∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴DC=DE,故①正确;
在Rt△ACD和Rt△AED中,,
∴Rt△ACD≌Rt△AED(HL),
∴∠ADC=∠ADE,AC=AE,
∴DA平分∠CDE,故②正确;
BE+AC=BE+AE=AB,故④正确;
∵∠BAC+∠B=90°,
∠BDE+∠B=90°,
∴∠BAC=∠BDE,故⑤正确;
∵∠ADE+∠BAD=90°,而∠BAD≠∠B,
∴∠BDE≠∠ADE,
∴DE平分∠ADB错误,故③错误;
综上所述,正确的有①②④⑤.
故答案为:①②④⑤.
【点评】本题考查了角平分线的性质的运用,全等三角形的判定与性质的运用;熟记角平分线的性质定理,证明三角形全等是解决问题的关键.
【考点】等边三角形的性质
【分析】根据已知条件先求出的长,再根据外角,直角算出△是等边三角形,同理可得出其他等边三角形,即可求出答案.
解:∵,,
∴
∵
∴
∴
∵
∴
∴△是等边三角形
∴
∴是等边三角形
∴
同理可得 是等边三角形
∴
【点评】本题考查了直角三角形计算,等腰三角形性质等知识点,发现线段之间的规律是解题关键.
1 、解答题
【考点】二次根式的混合运算
【分析】利用二次根式的乘法和除法法则即可求解.
解:
=
=.
【点评】本题考查二次根式的乘除法,解题的关键是掌握二次根式的乘法法则和除法法则.
【考点】分式的化简求值
【分析】根据分式的减法法则把原式化简,根据分式有意义的条件确定a的值,代入计算即可
解:原式=×+
=+
=,
当a=2时,原式==5.
【点评】本题考查的是分式的化简求值、分式有意义的条件,掌握分式的加减混合运算法则是解题的关键.
【考点】解分式方程,解一元一次不等式组
【分析】(1)先求出各不等式的解集,再求其公共解集即
(2)观察可得最简公分母是2(3x-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解
解:(1)解不等式
解不等式①得:x≤1
解不等式②,得:x>-2,
所以原不等式组的解集为-2(2)方程的两边同乘2(3x-1),得6(3x-1)-2=-4
解得x=
检验:把x=代入2(3x-1)≠0
所以原方程的解为:x=
【点评】此题考查解一元一次不等式组,解分式方程,解题关键在于熟练掌握运算法则
【考点】平行线的判定,全等三角形的性质
【分析】(1)利用全等三角形的性质即可判断;
(2)结论:AD=BC.只要证明∠ADB=∠CBD即可;
解:(1)∵△ADF≌△CBE,
∴AD=BC(全等三角形的对应边相等),
故答案为AD=BC,全等三角形的对应边相等;
(2)结论:AD∥BC.
理由:∵△ADF≌△CBE,
∴∠ADF=CBE,
∴∠ADB=∠CBD,
∴AD∥BC.
【点评】本题考查全等三角形的性质、平行线的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【考点】分式方程的应用.
【分析】(1)首先得出两人之间的速度之间关系,进而利用小明从起点向后退6m,得出两人的速度差,求出即可;
(2)利用两人的速度关系得出符合题意的方案.
解:(1)根据题意,得=,则y=x.
因为﹣=﹣=﹣<0,
所以<
所以小明先到达终点.
(2)方案一:小明在起点,小莉在起点前6米处,两人同时起跑,同时到达;
方案二:设小莉在起点,小明在起点后a米处,两人同时起跑,同时到达.
则=,
即=,
解得a=.
所以小莉在起点,小明在起点后米处,两人同时起跑,同时到达.
【点评】此题主要考查了分式方程的应用以及行程问题的相关的知识点;判断出两人的速度之比是解决本题的突破点.
【考点】等腰三角形的性质;线段垂直平分线的性质.
【分析】(1)证得△ABE≌△ACD后利用全等三角形的对应角相等即可证得结论;
(2)利用垂直平分线段的性质即可证得结论.
解:(1)∠ABE=∠ACD;
在△ABE和△ACD中,
,
∴△ABE≌△ACD,
∴∠ABE=∠ACD;
(2)∵AB=AC,
∴∠ABC=∠ACB,
由(1)可知∠ABE=∠ACD,
∴∠FBC=∠FCB,
∴FB=FC,
∵AB=AC,
∴点A.F均在线段BC的垂直平分线上,
即直线AF垂直平分线段BC.
【点评】本题考查了等腰三角形的性质及垂直平分线段的性质的知识,解题的关键是能够从题目中整理出全等三角形,难度不大.
【考点】一元一次不等式组的应用.
【分析】(1)这列货车挂A型车厢x节,则挂B型车厢(40﹣x)节,从而可得出y与x的表达式;
(2)设A型车厢x节,则挂B型车厢(40﹣x)节,根据所装的甲货物不少于1240吨,乙货物不少于880吨,可得出不等式组,解出即可.
解:(1)y=0.6x+0.8(40﹣x)=﹣0.2x+32;
(2)设A型车厢x,节,则挂B型车厢(40﹣x)节,
由题意得:,
解得:24≤x≤26,
故有三种方案:①A.B两种车厢的节数分别为24节、16节;
②A型车厢25节,B型车厢15节;
③A型车厢26节,B型车厢14节.
【点评】本题考查了一元一次不等式的应用,解答本题的关键是仔细审题,根据所装货物的不等关系,列出不等式组,难度一般.
【考点】全等三角形的判定与性质,等边三角形的判定与性质.
【分析】(2)证明△ABD≌△ACE(SAS)和△BAF≌△CAP(SAS),得AF=AP,∠BAF=∠CAP,再证明△AFP是等边三角形,最后由线段的和可得结论,
(3)如图③,在PC上截取CM=PB,连接AM,同理可得结论.
解:(2)PB=PA+PC,理由如下:
如图②,在BP上截取BF=PC,连接AF,
∵△ABC、△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠CAD+∠DAE,
即∠DAB=∠EAC,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,BF=CP,
∴△BAF≌△CAP(SAS),
∴AF=AP,∠BAF=∠CAP,
∴∠BAC=∠PAF=90°,
∴△AFP是等边三角形,
∴PF=PA,
∴PB=BF+PF=PC+PA,
(3)PC=PA+PB,理由如下:
如图③,在PC上截取CM=PB,连接AM,
同理得:△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,PB=CM,
∴△AMC≌△APB(SAS),
∴AM=AP,∠BAP=∠CAM,
∴∠BAC=∠PAM=60°,
∴△AMP是等边三角形,
∴PM=PA,
∴PC=PM+CM=PA+PB.
【点评】本题考查了等边三角形的性质、全等三角形的判定与性质等知识,熟练掌握等边三角形的性质,证明△ABD≌△ACE是解题的关键,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版2023-2024八年级上期末模拟试题1
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共10小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
下列结论正确的是( )
A.形状相同的两个图形是全等形
B.对应角相等的两个三角形是全等三角形
C.全等三角形的面积相等
D.两个等边三角形全等
计算,结果正确的是( )
A.1 B.x C. D.
如图,在△ABC中,D,E分别为BC上两点,且BD=DE=EC,则图中面积相等的三角形有( )对.
A. 4 B. 5 C. 6 D. 7
如图,在 Rt△ABC 中,∠C=90°,∠A=30°,若AB=8,则BC 等于 ( )
A.4 B.3 C.2 D.1
下列各数中比3大比4小的无理数是( )
A. B. C.3.1 D.
如图,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还添加一个条件才能使△ABC≌△DEF,下列不能添加的条件是( )
A.∠B=∠E B.BC=EF C.∠C=∠F D.AC=DF
如图,在△ABC中,∠A=50°,AD为∠A的平分线,DE⊥AB,DF⊥AC,则∠DEF=( )
A.15° B.25° C.35° D.20°
《九章算术》中记录的一道题目译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马速度的2倍,求规定时间.设规定时间为x天,所列方程正确的是( )
A.×2= B.=×2 C.×2= D.=×2
(﹣2)2008(+2)2007的值等于( )
A.2 B.﹣2 C. D.
如果不等式无解,则b的取值范围是( )
A.b>﹣2 B.b<﹣2 C.b≥﹣2 D.b≤﹣2
1 、填空题(本大题共8小题,每小题3分,共18分)
8的立方根等于 .
如图,∠A+∠B+∠C+∠D+∠E的度数为 度.
化简:(+) = .
数式的最大值为 ,此时x= .
如图,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上.请在这个网格中作线段AB的垂直平分线.要求:①仅用无刻度直尺,且不能用直尺中的直角;②保留必要的作图痕迹.
对非负实数x“四舍五入”到个位的值记为(x),即当n为非负整数时,若n﹣0.5≤x<n+0.5,则(x)=n.如(1.34)=1,(4.86)=5.若(0.5x﹣1)=6,则实数x的取值范围是 .
如图△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,给出下列结论:①DC=DE;②DA平分∠CDE;③DE平分∠ADB;④BE+AC=AB;⑤∠BAC=∠BDE.其中正确的是______ (写序号)
如图,,在上截取.过点作,交于点,以点为圆心,为半径画弧,交于点;过点作,交于点,以点为圆心,为半径画弧,交于点;按此规律,所得线段的长等于_______.
1 、解答题(本大题共8小题,共66分)
计算:
先化简,然后a在﹣1、1、2三个数中任选一个合适的数代入求值.
解方程或不等式组:(1);(2)
如图,△ADF≌△CBE,点E、B、D、F在同一条直线上.
(1)线段AD与BC之间的数量关系是 ,其数学根据是 .
(2)判断AD与BC之间的位置关系,并说明理由.
小明和小莉在跑道上进行100m短跑比赛,两人从出发点同时起跑,小明到达终点时,小莉离终点还差6m,已知小明和小莉的平均速度分别为x m/s、y m/s.
(1)如果两人重新开始比赛,小明从起点向后退6m,两人同时起跑能否同时到达终点?若能,请求出两人到达终点的时间;若不能,请说明谁先到达终点.
(2)如果两人想同时到达终点,应如何安排两人起跑位置?请设计两种方案.
如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A.F的直线垂直平分线段BC.
现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂在A.B两种不同规格的货车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元.
(1)设运送这批货物的总费用为y万元,这列货车挂A型车厢x节,试定出用车厢节数x表示总费用y的公式.
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A.B两种车厢的节数,那么共有哪几种安排车厢的方案?
△ABC和△ADE都是等边三角形.
(1)将△ADE绕点A旋转到图①的位置时,连接BD,CE并延长相交于点P(点P与点A重合),有PA+PB=PC(或PA+PC=PB)成立(不需证明),
(2)将△ADE绕点A旋转到图②的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA.PB、PC之间有怎样的数量关系?并加以证明,
(3)将△ADE绕点A旋转到图③的位置时,连接BD,CE相交于点P,连接PA,猜想线段PA.PB、PC之间有怎样的数量关系?直接写出结论,不需要证明.
答案解析
1 、选择题
【考点】全等图形的定义与性质
【分析】根据全等图形的定义对各选项分析判断后利用排除法求解.
解:A.应为形状相同,大小相等的两个图形是全等形,故本选项错误;
B、应为对应角相等,对应边相等的两个三角形是全等三角形,故本选项错误;
C、全等三角形的面积相等,正确,故本选项正确;
D、应为两个边长相等的等边三角形全等,故本选项错误.
故选C.
【点评】本题考查了全等图形的定义,以及全等三角形的性质,要注意从形状和大小两个方面考虑求解.
【考点】分式的加减法
【分析】根据分式的运算法则即可求出答案.
解:原式=
=1
故选:A.
【点评】本题考查分式的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.
【考点】三角形的角平分线、中线和高
【分析】根据三角形的面积公式,知:只要同底等高,则两个三角形的面积相等,据此可得面积相等的三角形.
解:由已知条件,得△ABD,△ADE,△ACE,3个三角形的面积都相等,组成了3对,
还有△ABE和△ACD的面积相等,共4对.
故选A.
【点评】本题考查了三角形的相关知识,解题的关键是熟练的掌握三角形面积公式与运用.
【考点】含30度角的直角三角形
【分析】根据含30度角的直角三角形的性质解答即可
解:根据含30度角的直角三角形的性质可知:BC=AB=4cm.
故选A
【点评】本题考查了含30度角的直角三角形,记住含30度角的直角三角形的性质是解题的关键.
【考点】算术平方根,无理数,实数大小比较
【分析】由于带根号的要开不尽方是无理数,无限不循环小数为无理数,根据无理数的定义即可求解.
解:∵四个选项中是无理数的只有和,而>4,3<<4
∴选项中比3大比4小的无理数只有.
故选:A.
【点评】此题主要考查了无理数的定义,解题时注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.
【考点】全等三角形的判定.
【分析】利用判定两个三角形全等的方法SSS、SAS、ASA.AAS、HL进行分析.
解:A.添加∠B=∠E,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
B、添加BC=EF,不能判定△ABC≌△DEF,故此选项符合题意;
C、添加∠C=∠F,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
D、添加AC=DF,可利用SAS定理判定△ABC≌△DEF,故此选项不合题意;
故选:B.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA.AAS、HL.
注意:AAA.SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
【考点】角平分线的性质;等腰三角形的判定与性质.
【分析】根据角平分线性质得出DE=DF,求出∠AAED=∠AFD=90°,求出∠EDF,根据等腰三角形性质和三角形的内角和定理求出即可.
解:∵AD为∠A的平分线,DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,DE=DF,
∵∠EDF=360°﹣∠AED﹣∠AFD﹣∠BAC=360°﹣90°﹣90°﹣50°=130°,
∵DE=DF,
∴∠DEF=∠DFE=(180°﹣∠EDF)=×(180°﹣130°)=25°,
故选B.
【点评】本题考查了等腰三角形性质,多边形的内角和定理,等腰三角形的性质的应用,注意:角平分线上的点到角两边的距离相等.
【考点】由实际问题抽象出分式方程,数学常识.
【分析】根据用快、慢马送所需时间与规定时间之间的关系,可得出用慢马送需要(x+1)天,用快马送需要(x﹣3)天,利用速度=路程÷时间,结合快马的速度是慢马速度的2倍,即可列出关于x的分式方程,此题得解.
解:∵用慢马送,需要的时间比规定时间多一天,用快马送,所需的时间比规定时间少3天,且规定时间为x天,
∴用慢马送需要(x+1)天,用快马送需要(x﹣3)天.
根据题意得:×2=.
故选:A.
【点评】本题考查了由实际问题抽象出分式方程以及数学常识,找准等量关系,正确列出分式方程是解题的关键.
【考点】二次根式的乘除法
【分析】根据am bm=(ab)m,先把原式化简后再求值.
解:原式=(﹣2)(﹣2)2007(+2)2007
=(﹣2)×(﹣1)=2﹣.
故选D.
【点评】正确理解二次根式乘法、积的乘方法则是解答问题的关键.
【考点】解一元一次不等式组.
【分析】不等式组无解就是两个不等式的解集没有公共部分,可利用数轴进行求解.
解:x>﹣2在数轴上表示点﹣2右边的部分,x<b表示点b左边的部分.
当点b在﹣2这点或这点的左边时,两个不等式没有公共部分,即不等式组无解,
则b≤﹣2.
故选D.
【点评】本题考查不等式组中不等式的未知字母的取值,利用数轴能直观的得到,易于理解.
1 、填空题
【考点】立方根
【分析】根据立方根的定义得出,求出即可.
解:8的立方根是=2,
故答案为:2.
【点评】本题考查了对立方根的应用,注意:a的立方根是,其中a可以为正数、负数和0.
【考点】三角形的外角性质;三角形内角和定理.
【分析】如图连接CE,根据三角形的一个外角等于和它不相邻的两个内角和∠1=∠A+∠B=∠2+∠3,在△DCE中有∠D+∠2+∠DCB+∠3+∠AED=180°,即可得∠D+∠A+∠DCB+∠B+∠AED=180°.
解:如图连接CE,
根据三角形的外角性质得∠1=∠A+∠B=∠2+∠3,
在△DCE中有,∠D+∠2+∠DCB+∠3+∠AED=180°,
∴∠D+∠A+∠DCB+∠B+∠AED=180°.
【点评】 本题运用三角形的一个外角等于和它不相邻的两个内角和,将已知角转化在同一个三角形中,再根据三角形内角和定理求解.
【考点】分式的混合运算.
【分析】首先计算括号內的加法,然后计算乘法即可化简.
解:原式=(﹣)
=
=1.
故答案为1.
【考点】二次根式的定义
【分析】根据算术平方根的性质可以得到≥0,即最小值是0,据此即可确定原式的最大值.
解:≥0,
∴当x=±2时,有最小值0,
则当x=±2,3-有最大值是3.
故答案是:3,±2.
【点评】本题考查了二次根式性质,理解≥0是关键.
【考点】 作图—应用与设计作图; 线段垂直平分线的性质.
【分析】以AB为边作正方形ABCD,正方形ABEF,连接AC,BD交于O,连接AE,BF交于O′,过O,O′作直线OO′于是得到结论.
解:如图所示,直线OO′即为所求.
【点评】本题考查了作图-应用与设计作图,正方形的性质,线段的垂直平分线的性质,正确的作出图形是解题的关键.
【考点】一元一次不等式组的应用
【分析】根据题意得到:6﹣0.5≤0.5x﹣1<6+0.5,据此求得x的取值范围.
解:依题意得:6﹣0.5≤0.5x﹣1<6+0.5
解得13≤x<15.
故答案是:13≤x<15.
【点评】考查了一元一次不等式组的应用,解题的关键是得到关于x的不等式组6﹣0.5≤0.5x﹣1<6+0.5.
【考点】角平分线的性质;全等三角形的判定与性质
【分析】根据角平分线上的点到角的两边的距离相等可得DC=DE,判断①正确,然后利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应角相等可得∠ADC=∠ADE,判断②正确;全等三角形对应边相等可得AC=AE,然后求出BE+AC=AB,判断④正确;根据同角的余角相等求出∠BAC=∠BDE,判断⑤正确,并得到③错误.
解:∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴DC=DE,故①正确;
在Rt△ACD和Rt△AED中,,
∴Rt△ACD≌Rt△AED(HL),
∴∠ADC=∠ADE,AC=AE,
∴DA平分∠CDE,故②正确;
BE+AC=BE+AE=AB,故④正确;
∵∠BAC+∠B=90°,
∠BDE+∠B=90°,
∴∠BAC=∠BDE,故⑤正确;
∵∠ADE+∠BAD=90°,而∠BAD≠∠B,
∴∠BDE≠∠ADE,
∴DE平分∠ADB错误,故③错误;
综上所述,正确的有①②④⑤.
故答案为:①②④⑤.
【点评】本题考查了角平分线的性质的运用,全等三角形的判定与性质的运用;熟记角平分线的性质定理,证明三角形全等是解决问题的关键.
【考点】等边三角形的性质
【分析】根据已知条件先求出的长,再根据外角,直角算出△是等边三角形,同理可得出其他等边三角形,即可求出答案.
解:∵,,
∴
∵
∴
∴
∵
∴
∴△是等边三角形
∴
∴是等边三角形
∴
同理可得 是等边三角形
∴
【点评】本题考查了直角三角形计算,等腰三角形性质等知识点,发现线段之间的规律是解题关键.
1 、解答题
【考点】二次根式的混合运算
【分析】利用二次根式的乘法和除法法则即可求解.
解:
=
=.
【点评】本题考查二次根式的乘除法,解题的关键是掌握二次根式的乘法法则和除法法则.
【考点】分式的化简求值
【分析】根据分式的减法法则把原式化简,根据分式有意义的条件确定a的值,代入计算即可
解:原式=×+
=+
=,
当a=2时,原式==5.
【点评】本题考查的是分式的化简求值、分式有意义的条件,掌握分式的加减混合运算法则是解题的关键.
【考点】解分式方程,解一元一次不等式组
【分析】(1)先求出各不等式的解集,再求其公共解集即
(2)观察可得最简公分母是2(3x-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解
解:(1)解不等式
解不等式①得:x≤1
解不等式②,得:x>-2,
所以原不等式组的解集为-2
解得x=
检验:把x=代入2(3x-1)≠0
所以原方程的解为:x=
【点评】此题考查解一元一次不等式组,解分式方程,解题关键在于熟练掌握运算法则
【考点】平行线的判定,全等三角形的性质
【分析】(1)利用全等三角形的性质即可判断;
(2)结论:AD=BC.只要证明∠ADB=∠CBD即可;
解:(1)∵△ADF≌△CBE,
∴AD=BC(全等三角形的对应边相等),
故答案为AD=BC,全等三角形的对应边相等;
(2)结论:AD∥BC.
理由:∵△ADF≌△CBE,
∴∠ADF=CBE,
∴∠ADB=∠CBD,
∴AD∥BC.
【点评】本题考查全等三角形的性质、平行线的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【考点】分式方程的应用.
【分析】(1)首先得出两人之间的速度之间关系,进而利用小明从起点向后退6m,得出两人的速度差,求出即可;
(2)利用两人的速度关系得出符合题意的方案.
解:(1)根据题意,得=,则y=x.
因为﹣=﹣=﹣<0,
所以<
所以小明先到达终点.
(2)方案一:小明在起点,小莉在起点前6米处,两人同时起跑,同时到达;
方案二:设小莉在起点,小明在起点后a米处,两人同时起跑,同时到达.
则=,
即=,
解得a=.
所以小莉在起点,小明在起点后米处,两人同时起跑,同时到达.
【点评】此题主要考查了分式方程的应用以及行程问题的相关的知识点;判断出两人的速度之比是解决本题的突破点.
【考点】等腰三角形的性质;线段垂直平分线的性质.
【分析】(1)证得△ABE≌△ACD后利用全等三角形的对应角相等即可证得结论;
(2)利用垂直平分线段的性质即可证得结论.
解:(1)∠ABE=∠ACD;
在△ABE和△ACD中,
,
∴△ABE≌△ACD,
∴∠ABE=∠ACD;
(2)∵AB=AC,
∴∠ABC=∠ACB,
由(1)可知∠ABE=∠ACD,
∴∠FBC=∠FCB,
∴FB=FC,
∵AB=AC,
∴点A.F均在线段BC的垂直平分线上,
即直线AF垂直平分线段BC.
【点评】本题考查了等腰三角形的性质及垂直平分线段的性质的知识,解题的关键是能够从题目中整理出全等三角形,难度不大.
【考点】一元一次不等式组的应用.
【分析】(1)这列货车挂A型车厢x节,则挂B型车厢(40﹣x)节,从而可得出y与x的表达式;
(2)设A型车厢x节,则挂B型车厢(40﹣x)节,根据所装的甲货物不少于1240吨,乙货物不少于880吨,可得出不等式组,解出即可.
解:(1)y=0.6x+0.8(40﹣x)=﹣0.2x+32;
(2)设A型车厢x,节,则挂B型车厢(40﹣x)节,
由题意得:,
解得:24≤x≤26,
故有三种方案:①A.B两种车厢的节数分别为24节、16节;
②A型车厢25节,B型车厢15节;
③A型车厢26节,B型车厢14节.
【点评】本题考查了一元一次不等式的应用,解答本题的关键是仔细审题,根据所装货物的不等关系,列出不等式组,难度一般.
【考点】全等三角形的判定与性质,等边三角形的判定与性质.
【分析】(2)证明△ABD≌△ACE(SAS)和△BAF≌△CAP(SAS),得AF=AP,∠BAF=∠CAP,再证明△AFP是等边三角形,最后由线段的和可得结论,
(3)如图③,在PC上截取CM=PB,连接AM,同理可得结论.
解:(2)PB=PA+PC,理由如下:
如图②,在BP上截取BF=PC,连接AF,
∵△ABC、△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠CAD+∠DAE,
即∠DAB=∠EAC,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,BF=CP,
∴△BAF≌△CAP(SAS),
∴AF=AP,∠BAF=∠CAP,
∴∠BAC=∠PAF=90°,
∴△AFP是等边三角形,
∴PF=PA,
∴PB=BF+PF=PC+PA,
(3)PC=PA+PB,理由如下:
如图③,在PC上截取CM=PB,连接AM,
同理得:△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵AB=AC,PB=CM,
∴△AMC≌△APB(SAS),
∴AM=AP,∠BAP=∠CAM,
∴∠BAC=∠PAM=60°,
∴△AMP是等边三角形,
∴PM=PA,
∴PC=PM+CM=PA+PB.
【点评】本题考查了等边三角形的性质、全等三角形的判定与性质等知识,熟练掌握等边三角形的性质,证明△ABD≌△ACE是解题的关键,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
