等腰三角形第一课时
图片预览






文档简介
课件22张PPT。14.3.1
等腰三角形学习目标:
1、理解等腰三角形的有关概念
2、掌握等边对等角和等腰三角形三线合一的性质课前思考
什么是等腰三角形?
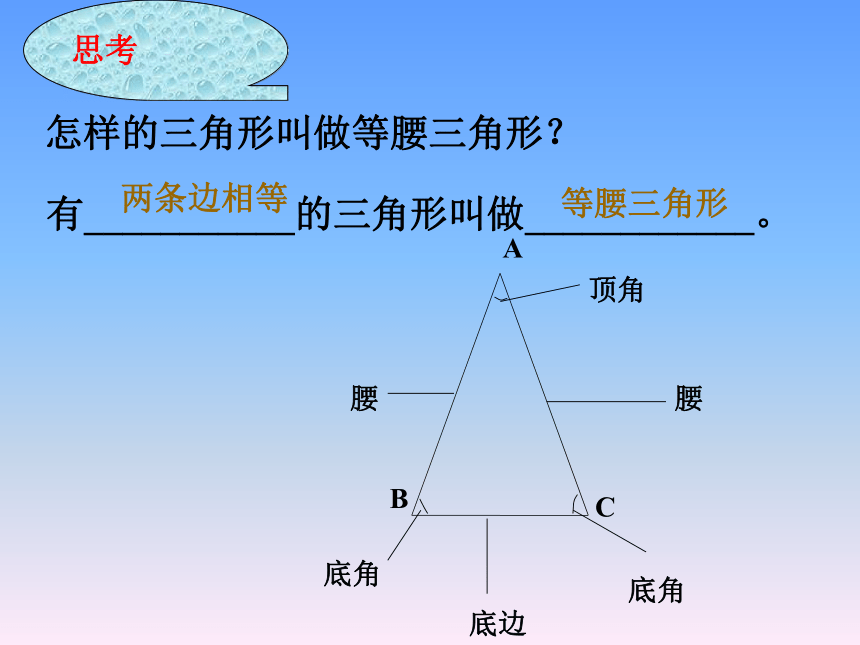
为什么我们要在轴对称这章里学习等腰三角形?怎样的三角形叫做等腰三角形?有___________的三角形叫做____________。思考两条边相等等腰三角形自学指导1
阅读课文:49页探究
自学要求:
1、按照探究要求,做出图形,并用字母标出相应的点
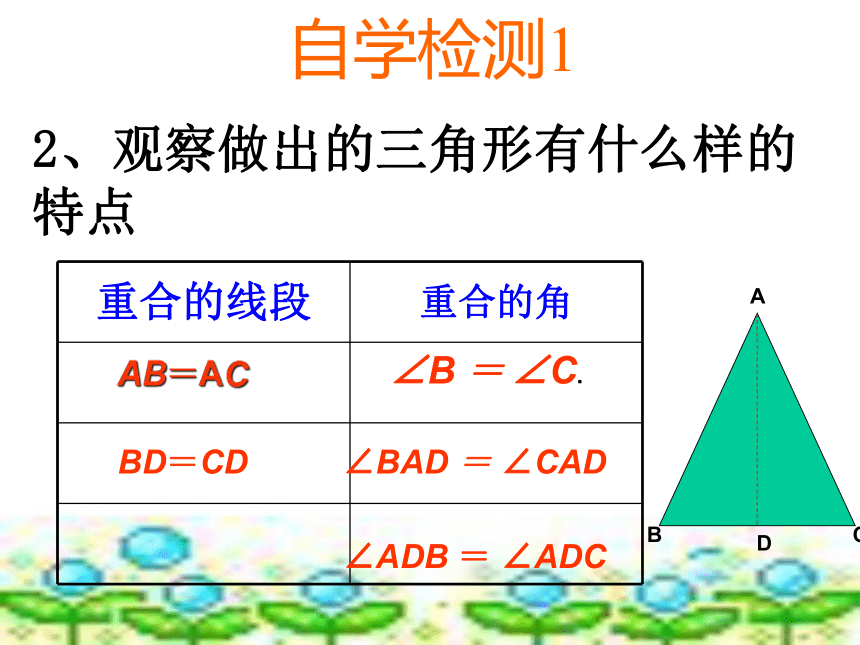
2、观察做出的三角形有什么样的特点(有哪些相等的线段和角) AC B D AB=AC BD=CD ∠B = ∠C.∠BAD = ∠CAD∠ADB = ∠ADC自学检测1
2、观察做出的三角形有什么样的特点自学指导2
阅读课文:50页
自学要求:细心观察书中是如何证明等腰三角形的两条性质。勾勒出你认为重要的语句。
3分钟后检测学习效果,板书证明过程。自学检测2
证明性质1:等腰三角形的两个底角相等(等边对等角)课本中是如何证明的?
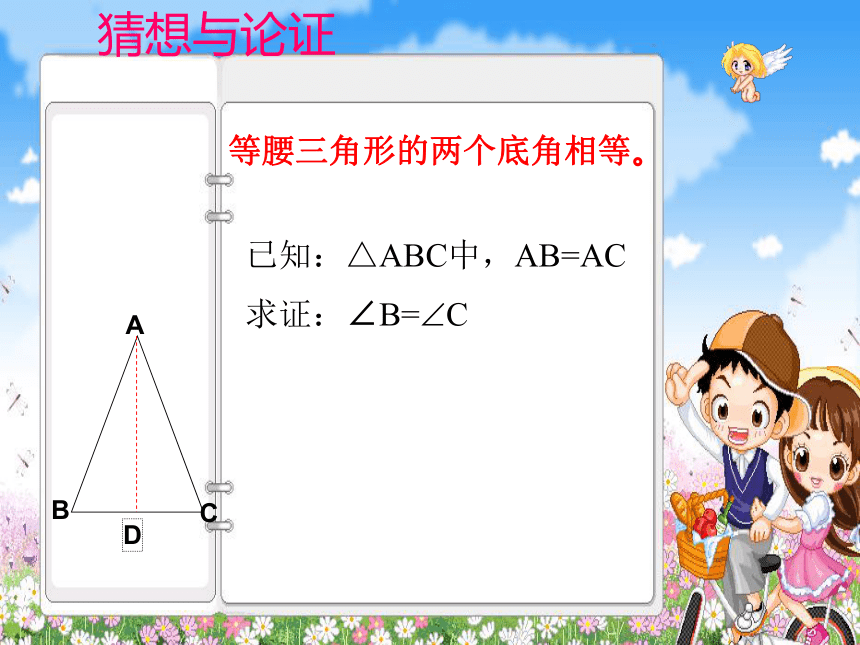
有没有其它办法?猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C则有 BD=CDD在△ABD和△ACD中证明: 作△ABC 的中线ADAB=AC BD=CDAD=AD (公共边) ∴ △ABD≌ △ACD (SSS) ∴ ∠B=∠C (全等三角形对应角相等) 方法一则有∠1=∠2D12在△ABD和△ACD中证明: 作顶角的平分线AD,AB=AC ∠1=∠2 AD=AD (公共边) ∴ △ABD≌ △ACD (SAS) ∴ ∠B=∠C (全等三角形对应角相等) 方法二则有 ∠ADB=∠ADC =90oD在Rt△ABD和Rt△ACD中证明: 作△ABC 的高线ADAB=AC AD=AD (公共边) ∴ Rt△ABD≌Rt△ACD (HL) ∴ ∠B=∠C (全等三角形对应角相等) 方法三自学检测2
证明性质2:等腰三角形顶角的平分线、底边的中线、底边上的高相互重合。(三线合一)等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练1 在三角形ABC中,已知AB=AC,且
∠ A=50° ,则∠B=——度,∠C=——度?∵AB=AC(已知)
∴∠B=∠C(等边对等角)又∵∠A+∠B+∠C=180° (三角形内角和为180° )
∠A=50° (已知)
∴∠B=65°
∠C=65°
等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练2 在等腰三角形ABC中,如果AB=AC,且一个角等于70° ,求另两个角的度数。解:若顶角即∠A=70° 则∠B=55 ° ∠C=55 °
若底角即∠B=70° 则∠C=70° ∠A=40°
若底角即∠C=70° 则∠B=70° ∠A=40°若改为90°呢?等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练3 :在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?∵AD ⊥BC(已知)
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线
合一)
∵BD=2cm(已知)
∴CD=2cm等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练5:在三角形ABC中,AB=AC,且AD ⊥BC,已知∠ 1=20°,求∠ 2=_____度。∵AD ⊥BC(已知)
∴ ∠ 1= ∠ 2 (等腰三角形的高与顶角的平分线重合)
即(等腰三角形三线
合一)
∵ ∠ 1=20° (已知)
∴ ∠ 2=20°等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)操练6 :已知AD⊥ BC,试找出等腰三角形ABC (AB=AC)中,存在相等关系的量。∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD小结:
本堂课主要学习了等腰三角形的两个性质:即等边对等角和等腰三角形三线合一。
只要知道等腰三角形的一个角的度数,我们就可以求出另外两个角的度数!
当堂作业P51练习1、2、3做到书上趣味数学:如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。选做题已知在等腰三角形ABC中,A=36° ,B=72° ,C=72° ,请同学们想一想,如何添一条线,将等腰三角形ABC分成两个等腰三角形?成功后,如何再添一条线,多得到一个等腰三角形?还可以继续吗?只要将做∠ B的角平分线即可!
只要再做∠ BDE的角平分线即可!
以下步骤重复下去即可!
等腰三角形学习目标:
1、理解等腰三角形的有关概念
2、掌握等边对等角和等腰三角形三线合一的性质课前思考
什么是等腰三角形?
为什么我们要在轴对称这章里学习等腰三角形?怎样的三角形叫做等腰三角形?有___________的三角形叫做____________。思考两条边相等等腰三角形自学指导1
阅读课文:49页探究
自学要求:
1、按照探究要求,做出图形,并用字母标出相应的点
2、观察做出的三角形有什么样的特点(有哪些相等的线段和角) AC B D AB=AC BD=CD ∠B = ∠C.∠BAD = ∠CAD∠ADB = ∠ADC自学检测1
2、观察做出的三角形有什么样的特点自学指导2
阅读课文:50页
自学要求:细心观察书中是如何证明等腰三角形的两条性质。勾勒出你认为重要的语句。
3分钟后检测学习效果,板书证明过程。自学检测2
证明性质1:等腰三角形的两个底角相等(等边对等角)课本中是如何证明的?
有没有其它办法?猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C则有 BD=CDD在△ABD和△ACD中证明: 作△ABC 的中线ADAB=AC BD=CDAD=AD (公共边) ∴ △ABD≌ △ACD (SSS) ∴ ∠B=∠C (全等三角形对应角相等) 方法一则有∠1=∠2D12在△ABD和△ACD中证明: 作顶角的平分线AD,AB=AC ∠1=∠2 AD=AD (公共边) ∴ △ABD≌ △ACD (SAS) ∴ ∠B=∠C (全等三角形对应角相等) 方法二则有 ∠ADB=∠ADC =90oD在Rt△ABD和Rt△ACD中证明: 作△ABC 的高线ADAB=AC AD=AD (公共边) ∴ Rt△ABD≌Rt△ACD (HL) ∴ ∠B=∠C (全等三角形对应角相等) 方法三自学检测2
证明性质2:等腰三角形顶角的平分线、底边的中线、底边上的高相互重合。(三线合一)等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练1 在三角形ABC中,已知AB=AC,且
∠ A=50° ,则∠B=——度,∠C=——度?∵AB=AC(已知)
∴∠B=∠C(等边对等角)又∵∠A+∠B+∠C=180° (三角形内角和为180° )
∠A=50° (已知)
∴∠B=65°
∠C=65°
等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练2 在等腰三角形ABC中,如果AB=AC,且一个角等于70° ,求另两个角的度数。解:若顶角即∠A=70° 则∠B=55 ° ∠C=55 °
若底角即∠B=70° 则∠C=70° ∠A=40°
若底角即∠C=70° 则∠B=70° ∠A=40°若改为90°呢?等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练3 :在三角形ABC中,AB=AC,且AD ⊥BC,已知BD=2cm,求DC=___cm, BC=___cm?∵AD ⊥BC(已知)
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线
合一)
∵BD=2cm(已知)
∴CD=2cm等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
操练5:在三角形ABC中,AB=AC,且AD ⊥BC,已知∠ 1=20°,求∠ 2=_____度。∵AD ⊥BC(已知)
∴ ∠ 1= ∠ 2 (等腰三角形的高与顶角的平分线重合)
即(等腰三角形三线
合一)
∵ ∠ 1=20° (已知)
∴ ∠ 2=20°等腰三角形的性质
1 等腰三角形的两个底角相等(等边对等角)
2等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)操练6 :已知AD⊥ BC,试找出等腰三角形ABC (AB=AC)中,存在相等关系的量。∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD小结:
本堂课主要学习了等腰三角形的两个性质:即等边对等角和等腰三角形三线合一。
只要知道等腰三角形的一个角的度数,我们就可以求出另外两个角的度数!
当堂作业P51练习1、2、3做到书上趣味数学:如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。选做题已知在等腰三角形ABC中,A=36° ,B=72° ,C=72° ,请同学们想一想,如何添一条线,将等腰三角形ABC分成两个等腰三角形?成功后,如何再添一条线,多得到一个等腰三角形?还可以继续吗?只要将做∠ B的角平分线即可!
只要再做∠ BDE的角平分线即可!
以下步骤重复下去即可!
