【新青岛版】八年级数学下册:10.6《一次函数的应用》导学案
文档属性
| 名称 | 【新青岛版】八年级数学下册:10.6《一次函数的应用》导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 24.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-30 00:00:00 | ||
图片预览


文档简介
10.6一次函数的应用
【学习目标】
1.体会应用一次函数的知识解决有关的实际问题的作用,增强应用函数知识解决实际问题的意识;
2.感知不等式、函数、方程的不同作用与内在联系,培养分析问题、解决问题的能力。
【课前预习】
阅读教材P154---P156的内容,与同学交流下列问题:
1.若直线y=kx+6与两坐标轴所围成的三角形面积是24,求常数k的值是多少?
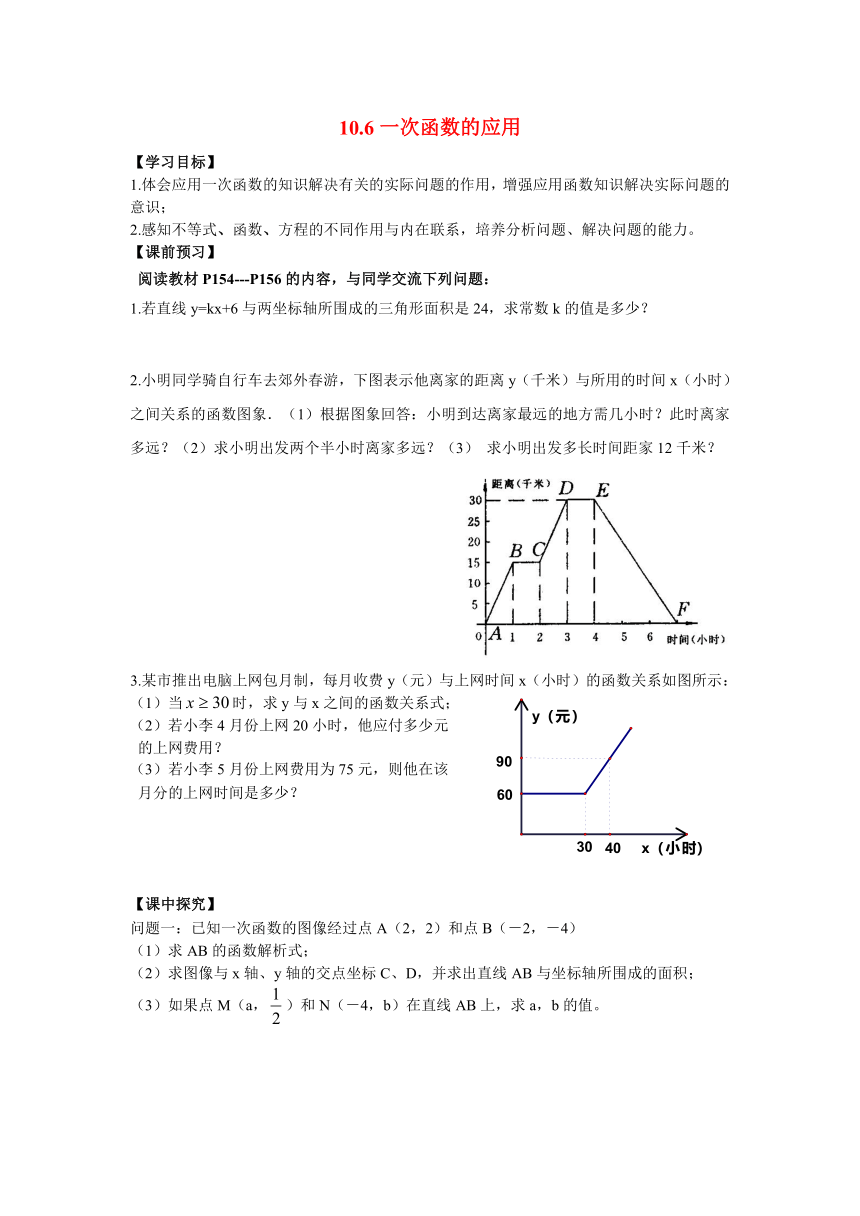
2.小明同学骑自行车去郊外春游,下图表示 ( http: / / www.21cnjy.com )他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?(2)求小明出发两个半小时离家多远?(3)求小明出发多长时间距家12千米?
( http: / / www.21cnjy.com )
3.某市推出电脑上网包月制,每月收费y(元)与上网时间x(小时)的函数关系如图所示:
(1)当时,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元
的上网费用?
若小李5月份上网费用为75元,则他在该
月分的上网时间是多少?
【课中探究】
问题一:已知一次函数的图像经过点A(2,2)和点B(-2,-4)
(1)求AB的函数解析式;
(2)求图像与x轴、y轴的交点坐标C、D,并求出直线AB与坐标轴所围成的面积;
(3)如果点M(a,)和N(-4,b)在直线AB上,求a,b的值。
问题二:大拇指与小拇指尽量张开时,两指尖的距离称为指距。某研究表明,一般人的身高h时指距d的一次函数,下表中是测得的指距与身高的一组数据:
指距d(cm) 20 21 22 23
身高h(cm) 160 169 178 187
求出h与d之间的函数关系式
某人身高为196cm,则一般情况下他的指距应为多少?
问题三:李晖到“宁泉牌”服装专卖店做社会调 ( http: / / www.21cnjy.com )查.了解到商店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员 小俐 小花
月销售件数(件) 200 150
月总收入(元) 1400 1250
假设月销售件数为x件,月总收入为y元,销售1件奖励a元,营业员月基本工资为b元.
(1)求a,b的值;
(2)若营业员小俐某月总收入不低于1800元,则小俐当月至少要卖服装多少件?
谈一谈:本节课你学得了哪些知识与方法?
【当堂检测】
1.兄弟俩赛跑,哥哥先让弟弟跑9 m,然后 ( http: / / www.21cnjy.com )自己才开始跑,已知弟弟每秒跑3 m,哥哥每秒跑4 m,列出函数关系式,画出函数图象,观察图象回答下列问题:
(1)当_________时,弟弟跑在哥哥前面;
(2)当________时,哥哥跑在弟弟前面;
(3)________先跑过20m,_______先跑过100m;
(4)你是怎样求解的?与同伴交流
2.商场某种毛笔每枝售价25元,书法练习本每本售价5元.该商场为促销,制定了两种优惠办法:
甲:买一枝毛笔赠送一本书法练习本;
乙:按购买金额打九折付款.
学校书法兴趣小组欲购买这种毛笔10枝,书法练习本本.
(1)分别写出每种优惠办法实际付款的金额(元)、(本)之间的函数解析式;
(2)比较购买同样多的书法练习本时,按哪种优惠办法更省钱?
3.某种铂金饰品在甲、乙两 ( http: / / www.21cnjy.com )个商店销售.甲店标价477元/克,按标价出售,不优惠.乙店标价530元/克,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.
⑴ 分别写出到甲、乙商店购买该种铂金饰品所需费用(元)和重量(克)之间的函数关系式;
⑵ 李阿姨要买一条重量不少于4克且不超过10克的此种铂金饰品,到哪个商店购买最合算?
【课后巩固】
1.直线y=kx+b经过一、二、四象限,则直线y=-bx+k不经过第____象限.
2.已知等腰三角形周长为20,写出底边长y关于腰长x的函数解析式(x为自变量),并写出自变量取值范围,画出函数图象.
3.已知A(8,0)及在第一象限的动点 ( http: / / www.21cnjy.com )P(x,y),且x+y=10,设△OPA的面积为S.(1)求S关于x的函数解析式;(2)求x的取值范围;(3)求S=12时P点坐标;。
4.某果品公司欲请汽车运输公司或火 ( http: / / www.21cnjy.com )车货运站将60吨水果从A地运到B地。已知汽车和火车从A地到B地的运输路程均为s千米。这两家运输单位在运输过程中,除都要收取运输途中每吨每小时5元的冷藏费外,要收取的其它费用及有关运输资料由下表给出:
运输工具 行驶速度(千米/小时) 运费单价(元/吨千米) 装卸总费用(元)
汽车 50 2 3000
火车 80 1.7 4620
说明:“1元/吨千米”表示“每吨每千米1元”
(1)请分别写出这两家运输单位运送这批水果所要收取的总费用y1(元)和y2(元)(用含s的式子表示);
(2)为减少费用,你认为果品公司应选择哪家运输单位运送这批水果更为合算?
5.在同一坐标系中画出一次函数y1=-2x+1与y2=2x-3的图象,并根据图象回答下列问题:
(1)直线y1=-2x+1、y2=2x-3与y轴分别交于点A、B,请写出A、B两点的坐标.
(2)写出直线y1=-2x+1与y2=2x-3的交点P的坐标.
(3)求△PAB的面积.
【学习目标】
1.体会应用一次函数的知识解决有关的实际问题的作用,增强应用函数知识解决实际问题的意识;
2.感知不等式、函数、方程的不同作用与内在联系,培养分析问题、解决问题的能力。
【课前预习】
阅读教材P154---P156的内容,与同学交流下列问题:
1.若直线y=kx+6与两坐标轴所围成的三角形面积是24,求常数k的值是多少?
2.小明同学骑自行车去郊外春游,下图表示 ( http: / / www.21cnjy.com )他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远?(2)求小明出发两个半小时离家多远?(3)求小明出发多长时间距家12千米?
( http: / / www.21cnjy.com )
3.某市推出电脑上网包月制,每月收费y(元)与上网时间x(小时)的函数关系如图所示:
(1)当时,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元
的上网费用?
若小李5月份上网费用为75元,则他在该
月分的上网时间是多少?
【课中探究】
问题一:已知一次函数的图像经过点A(2,2)和点B(-2,-4)
(1)求AB的函数解析式;
(2)求图像与x轴、y轴的交点坐标C、D,并求出直线AB与坐标轴所围成的面积;
(3)如果点M(a,)和N(-4,b)在直线AB上,求a,b的值。
问题二:大拇指与小拇指尽量张开时,两指尖的距离称为指距。某研究表明,一般人的身高h时指距d的一次函数,下表中是测得的指距与身高的一组数据:
指距d(cm) 20 21 22 23
身高h(cm) 160 169 178 187
求出h与d之间的函数关系式
某人身高为196cm,则一般情况下他的指距应为多少?
问题三:李晖到“宁泉牌”服装专卖店做社会调 ( http: / / www.21cnjy.com )查.了解到商店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员 小俐 小花
月销售件数(件) 200 150
月总收入(元) 1400 1250
假设月销售件数为x件,月总收入为y元,销售1件奖励a元,营业员月基本工资为b元.
(1)求a,b的值;
(2)若营业员小俐某月总收入不低于1800元,则小俐当月至少要卖服装多少件?
谈一谈:本节课你学得了哪些知识与方法?
【当堂检测】
1.兄弟俩赛跑,哥哥先让弟弟跑9 m,然后 ( http: / / www.21cnjy.com )自己才开始跑,已知弟弟每秒跑3 m,哥哥每秒跑4 m,列出函数关系式,画出函数图象,观察图象回答下列问题:
(1)当_________时,弟弟跑在哥哥前面;
(2)当________时,哥哥跑在弟弟前面;
(3)________先跑过20m,_______先跑过100m;
(4)你是怎样求解的?与同伴交流
2.商场某种毛笔每枝售价25元,书法练习本每本售价5元.该商场为促销,制定了两种优惠办法:
甲:买一枝毛笔赠送一本书法练习本;
乙:按购买金额打九折付款.
学校书法兴趣小组欲购买这种毛笔10枝,书法练习本本.
(1)分别写出每种优惠办法实际付款的金额(元)、(本)之间的函数解析式;
(2)比较购买同样多的书法练习本时,按哪种优惠办法更省钱?
3.某种铂金饰品在甲、乙两 ( http: / / www.21cnjy.com )个商店销售.甲店标价477元/克,按标价出售,不优惠.乙店标价530元/克,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.
⑴ 分别写出到甲、乙商店购买该种铂金饰品所需费用(元)和重量(克)之间的函数关系式;
⑵ 李阿姨要买一条重量不少于4克且不超过10克的此种铂金饰品,到哪个商店购买最合算?
【课后巩固】
1.直线y=kx+b经过一、二、四象限,则直线y=-bx+k不经过第____象限.
2.已知等腰三角形周长为20,写出底边长y关于腰长x的函数解析式(x为自变量),并写出自变量取值范围,画出函数图象.
3.已知A(8,0)及在第一象限的动点 ( http: / / www.21cnjy.com )P(x,y),且x+y=10,设△OPA的面积为S.(1)求S关于x的函数解析式;(2)求x的取值范围;(3)求S=12时P点坐标;。
4.某果品公司欲请汽车运输公司或火 ( http: / / www.21cnjy.com )车货运站将60吨水果从A地运到B地。已知汽车和火车从A地到B地的运输路程均为s千米。这两家运输单位在运输过程中,除都要收取运输途中每吨每小时5元的冷藏费外,要收取的其它费用及有关运输资料由下表给出:
运输工具 行驶速度(千米/小时) 运费单价(元/吨千米) 装卸总费用(元)
汽车 50 2 3000
火车 80 1.7 4620
说明:“1元/吨千米”表示“每吨每千米1元”
(1)请分别写出这两家运输单位运送这批水果所要收取的总费用y1(元)和y2(元)(用含s的式子表示);
(2)为减少费用,你认为果品公司应选择哪家运输单位运送这批水果更为合算?
5.在同一坐标系中画出一次函数y1=-2x+1与y2=2x-3的图象,并根据图象回答下列问题:
(1)直线y1=-2x+1、y2=2x-3与y轴分别交于点A、B,请写出A、B两点的坐标.
(2)写出直线y1=-2x+1与y2=2x-3的交点P的坐标.
(3)求△PAB的面积.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
