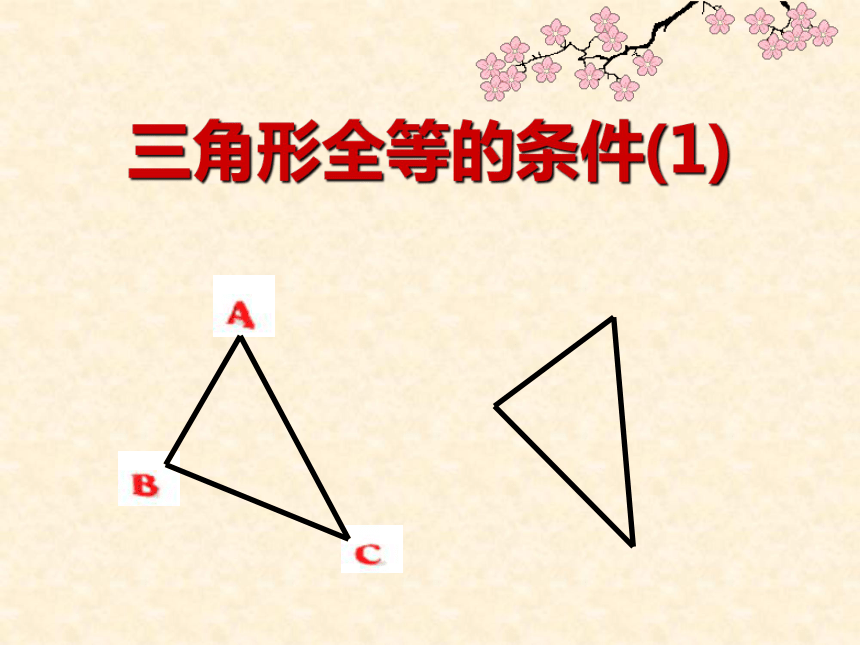
数学七年级下人教版(五四制)18.2三角形全等的条件课件
文档属性
| 名称 | 数学七年级下人教版(五四制)18.2三角形全等的条件课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 五四学制版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-30 00:00:00 | ||
图片预览

文档简介
课件78张PPT。三角形全等的条件(1) 1、全等三角形的 相等,
相等。
2、如图1,已知△AOC≌△BOD,
则∠A=∠B,∠C= ,
=∠2,
对应边有AC= , =OB,
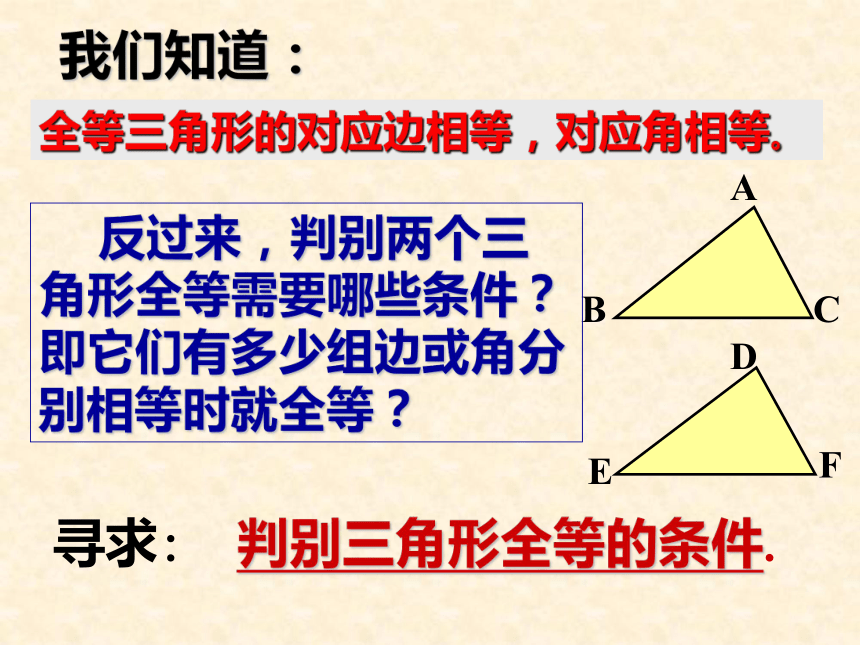
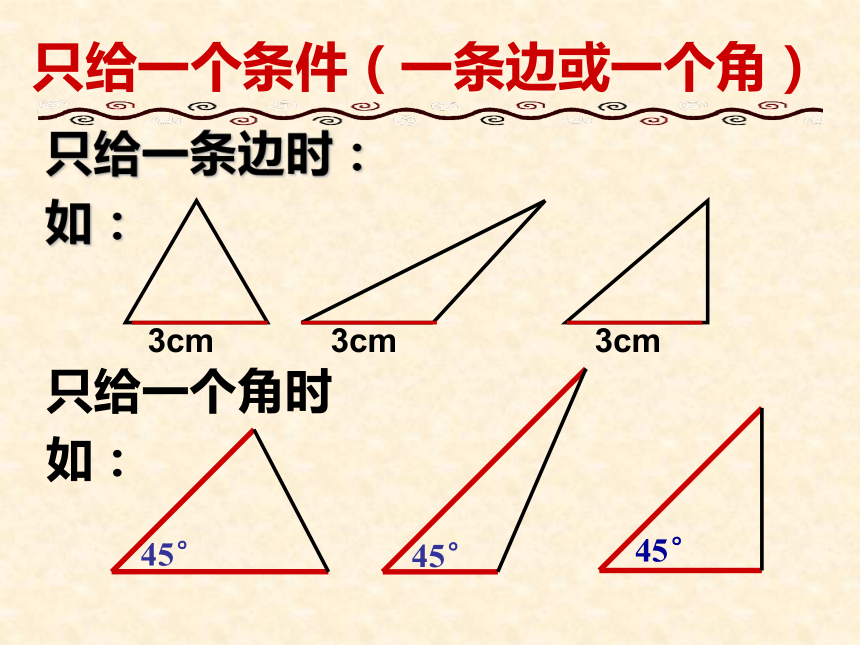
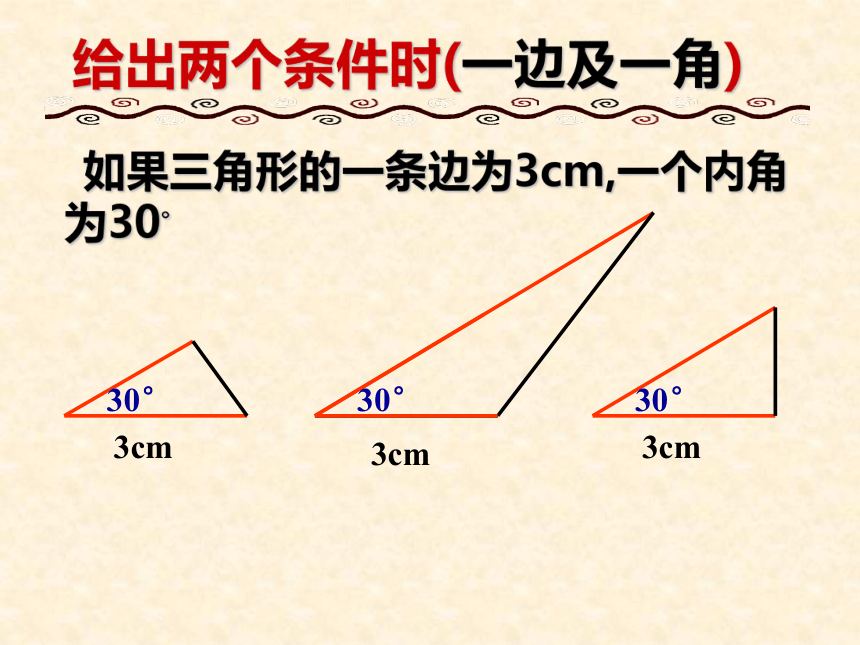
=OD。对应边对应角∠D∠1BDOAOC全等三角形的对应边相等,对应角相等。我们知道: 反过来,判别两个三角形全等需要哪些条件? 即它们有多少组边或角分别相等时就全等?寻求: 判别三角形全等的条件.只给一个条件(一条边或一个角)只给一条边时:
如:3cm3cm3cm只给一个角时
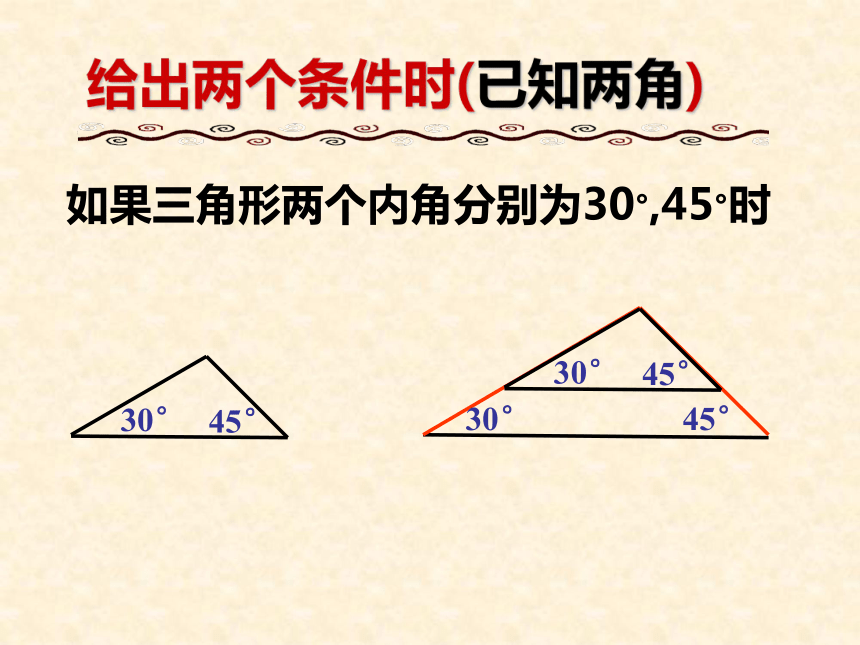
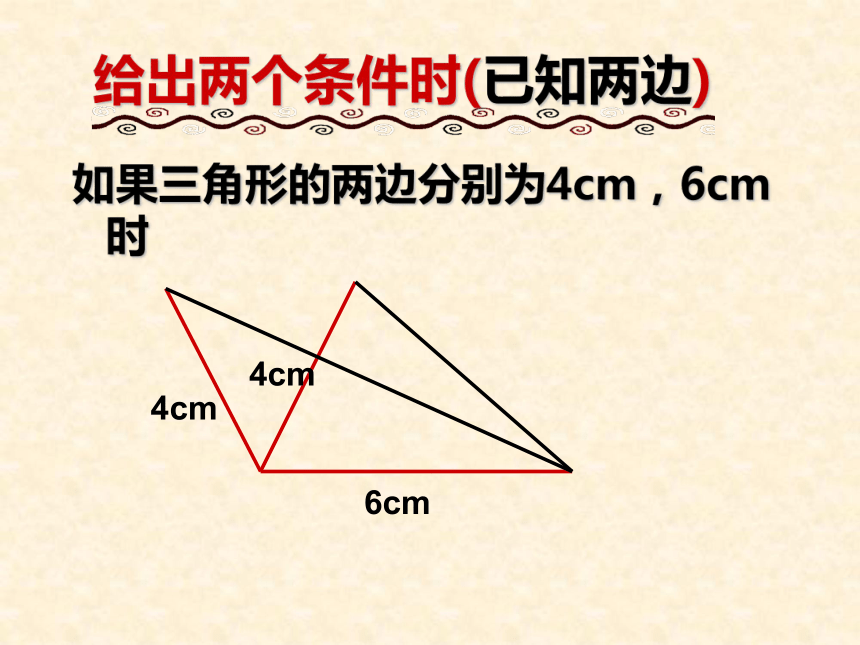
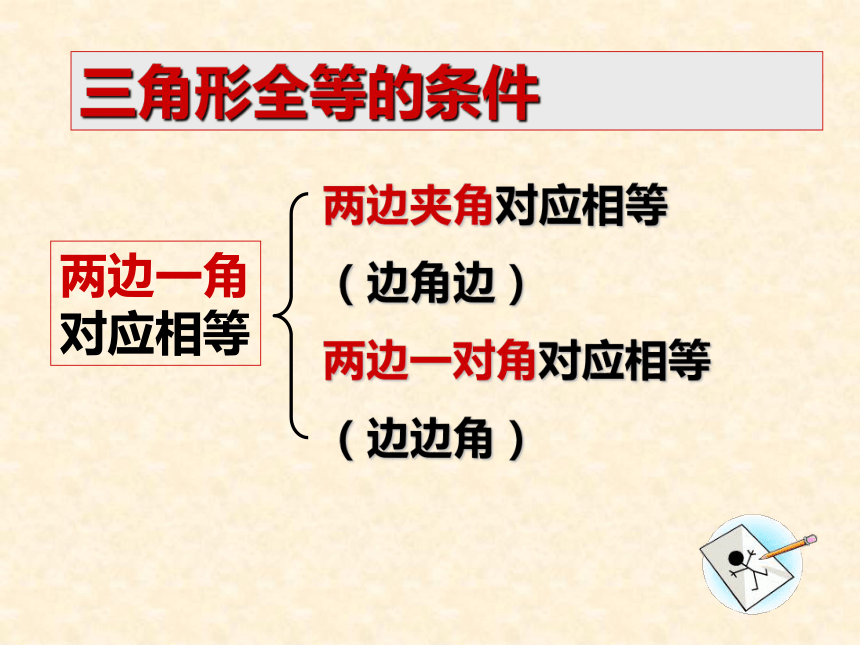
如:45°45°45° 如果三角形的一条边为3cm,一个内角为30°3cm3cm3cm30°30°30°给出两个条件时(一边及一角)给出两个条件时(已知两角)如果三角形两个内角分别为30°,45°时30°45°给出两个条件时(已知两边)如果三角形的两边分别为4cm,6cm 时6cm4cm4cm三角形全等的条件两边一角对应相等两边夹角对应相等
(边角边) 两边一对角对应相等
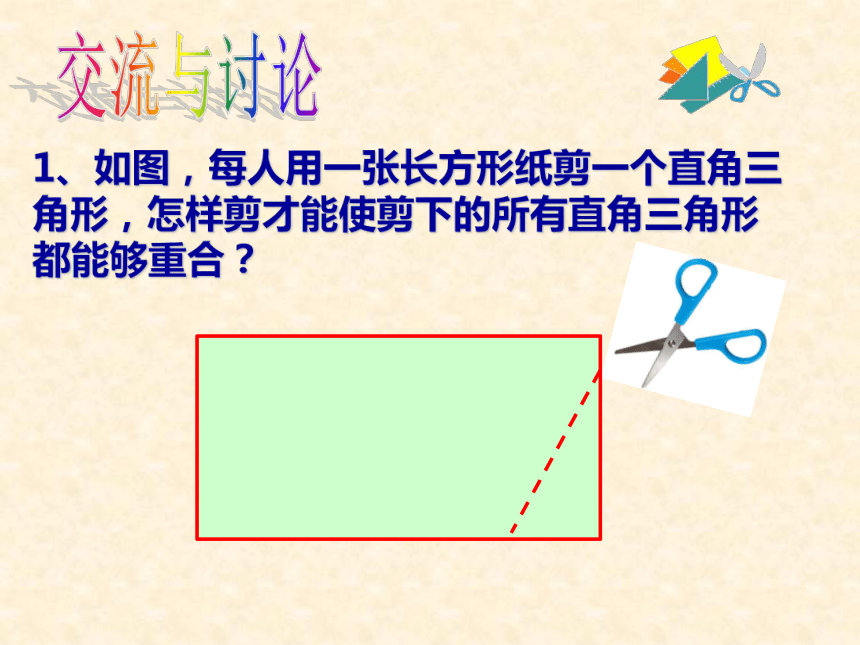
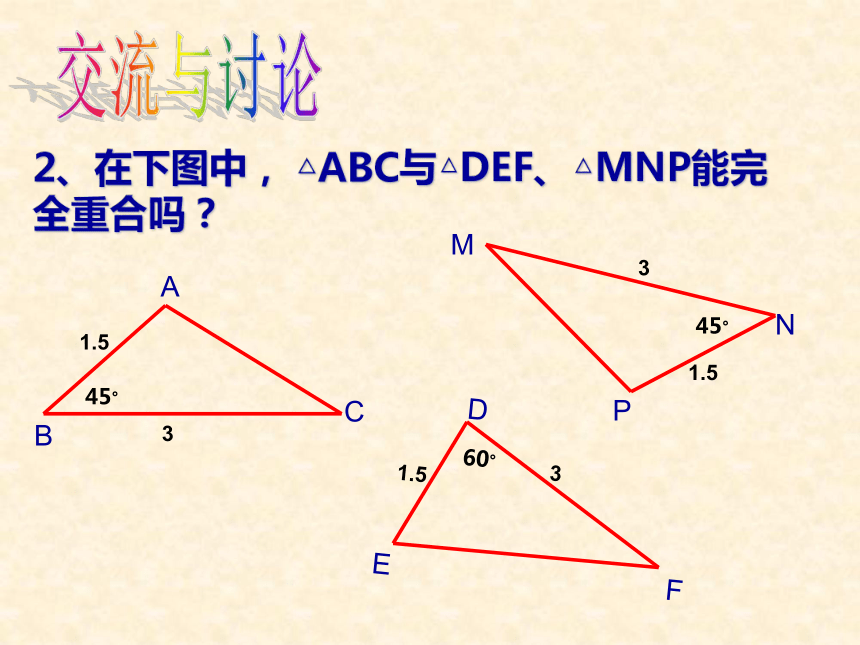
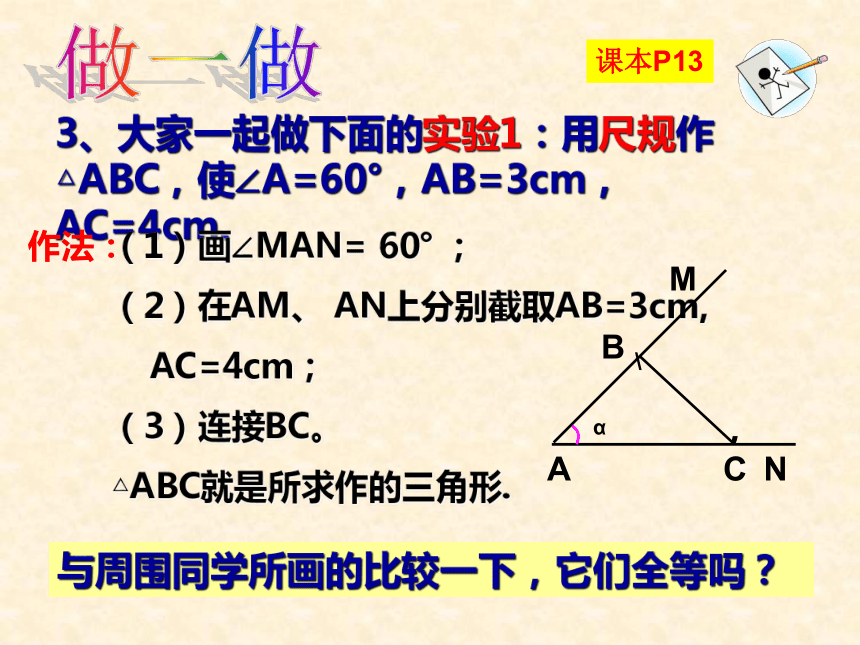
(边边角)交流与讨论1、如图,每人用一张长方形纸剪一个直角三角形,怎样剪才能使剪下的所有直角三角形都能够重合?交流与讨论2、在下图中, △ABC与△DEF、△MNP能完全重合吗?3、大家一起做下面的实验1:用尺规作△ABC,使∠A=60°,AB=3cm,AC=4cm. (1)画∠MAN= 60° ;
(2)在AM、 AN上分别截取AB=3cm,
AC=4cm;
(3)连接BC。
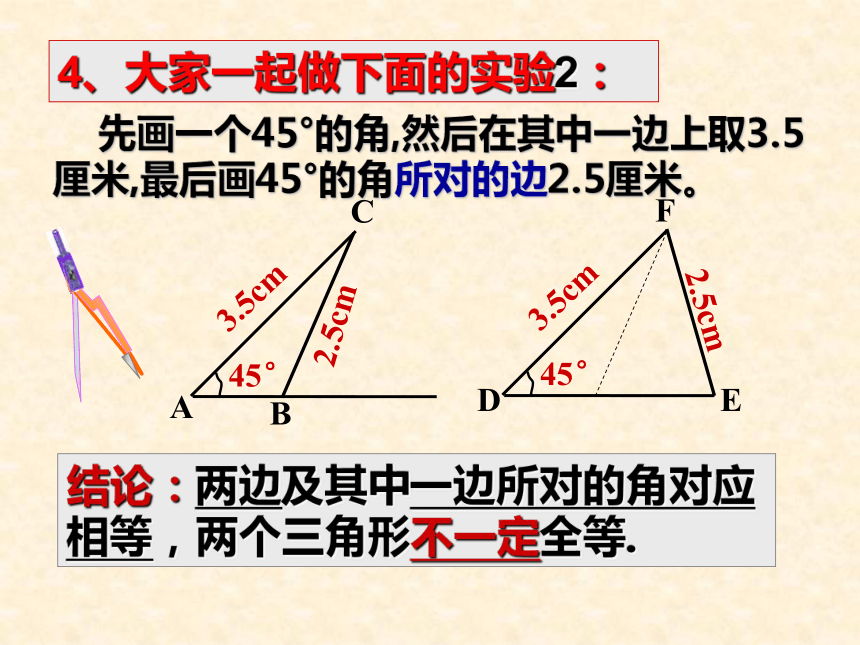
△ABC就是所求作的三角形.CB′做一做与周围同学所画的比较一下,它们全等吗?课本P13α作法:结论:两边及其中一边所对的角对应相等,两个三角形不一定全等. 先画一个45°的角,然后在其中一边上取3.5厘米,最后画45°的角所对的边2.5厘米。4、大家一起做下面的实验2:两边一角对应相等两边夹角对应相等
(边角边) 两边一对角对应相等
(边边角)(×)(√)再次明确实践告诉我们判定两个三角形全等的一个基本事实:两边及其夹角分别相等的两个三角形全等(可简写为“边角边”或“SAS”)在△ABC和△ DEF中,
AB = DE
∠B =∠E
BC = EF
∴ △ABC≌△DEF (SAS) 几何语言:两边及其夹角分别相等的两个三角形全等(可简写为“边角边”或“SAS”)已知:如图, AB=AD ,∠BAC=∠DAC
求证:△ABC≌△ADC .解:AB=AD (已知)∠BAC=∠DAC (已知)AC=AC(公共边)∵ 在△ABC 和△ADC中∴ △ABC ≌△ADC (SAS)注意:1、 要充分利用图形中“公共边”这个条件.
2、 △ABC沿直线AC翻折后能够与△ADC重合.归纳:判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。 现在例1的已知条件不改变, 而问题改变成: “DC与BC相等吗”, 如何作答?……
∴ △ABC ≌△ADC (SAS)
∴ DC=BC (全等三角形的对应边相等)证明三角形全等的步骤:?1.写出在哪两个三角形中证明全等。(注意把表示对应顶点的字母写在对应的位置上).
?2.按边、角、边的顺序列出三个条件,用大括号合在一起.
?3.写出结论.每步要有推理的依据.1、在下列三角形中,哪两个三角形全等?40°4430°444640°⑴⑵⑶⑷⑸⑹解: 全等的三角形有:⑴和⑷, ⑶和⑸.P14练一练:课堂练习2、已知:如图,AB=AC,点D、E分别在AB、AC上,且AD=AE.
求证:△ABE≌△ACD.注意: 要充分利用图形中“公共角”这个条件.你还能得到哪些相等的线段?说明理由.3、已知:如图,AC与BD相交于点O,且OA=OC,OB=OD,
求证:△AOB≌△COD注意: 要充分利用图形中“对顶角相等”这个条件. 小结:1 两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”2 两边以及其中一边的对角对应相等的两个三角形不一定全等.注意: 要充分利用图形中 “对顶角,公共角,公共边”这些条件.3 判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。1.3探索三角形全等的条件(2)习题课∵在△ABC和△ DEF中,
AB = DE
∠B =∠E
BC = EF
∴ △ABC≌△DEF (SAS) 几何语言:两边及其夹角分别相等的两个三角形全等(可简写为“边角边”或“SAS”)复习回顾例1、判断题:
(1)有2条边对应相等的2个三角形全等。( )
(2)有两边和1个角对应相等的2个三角形全等。( )
(3)2条直角边对应相等的2个直角三角形全等。( )
(4)边长相等的2个等边三角形全等。( ) √××√例题精讲已知:如图,AB、CD相交于点E,且点E是AB、CD的中点.
求证:△AEC≌△BED例题精讲例2思考:你能说明图中的AC∥DB吗?注意:△AEC绕点E旋转180°后可以与△BED重合。已知:如图,点E、F在CD上,且CE=DF,AE=BF,AE∥BF.
求证:△AEC≌△BFD例题精讲例3思考:
1、能够改变例3中△AEC的位置得到例2 的图形?
2、根据例3中的已知条件,你还能得到那些结论?1、课本P16 练习1、2、3
2、课本P29习题1.3 1、3
(作业:4、5给予提示)
课堂练习课本P29 习题1.33、如图,把两根钢条AA’、BB’的中点O连在一起,可以做成一个测量工件内槽宽的工具(这种工具叫做卡钳),只要量出A′B′的长度,就可以知道工件内径AB的长度是否符合标准。你能说出这样测量的理由吗? 先做P29第1题1、已知:如图,AD=AE,BD=CE,∠ADE=∠AED,
求证:△ADB≌△AEC. 思考:
若将条件“BD=CE”改成“BE=CD”能得到同样的结论吗?2、已知:如图,MP=MQ,MN=MG,
∠PMN=∠QMG.
求: 请在图中找出全等三角形,并说明理由。课堂小结通过本节课你学到了哪些知识?说一说你的收获吧!布置作业1、上本子:P30习题1.3 4、5
2、《评价手册》
3、《补充习题》三角形全等的条件(3)两角夹一边 ?两角及其中一角的对边 ?两角及一边两边及夹角 (SAS)判别三角形全等的三个条件:(已知两角及夹边)做一做 两角和它们的夹边对应相等的两个三角形全等.
简写成:“角边角”或“ASA”见书p17讨论 两角和它们的夹边对应相等的两个三角形全等.
简写成:“角边角”或“ASA”在△ABC和△ MNP中,
∠B =∠N
BC = NP
∠C=∠P
∴ △ABC≌△MNP (ASA) 几何语言:(已知两角和其中一角的对边)如图,在△ABC与△MNP中,∠A=∠M,∠B=∠N,BC=NP,△ABC与△MNP全等吗?为什么?想一想这里能将以上条件转化成“ASA”证明吗? 两角和其中一角的对边对应相等的两个三角形全等. 简写成:“角角边”或“AAS”几何语言:两角夹一边 (ASA)两角及其中一角的对边(AAS)两角及一边两边及夹角 (SAS)判别三角形全等的三个条件: (1) 如图,小明不慎将一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃吗? 如果可以,带哪块去合适? 你能说明其中理由吗?议一议①②两角和它们的夹边对应相等的两个三角形全等.○①②( )∵在 中例1: 如图,O是AB的中点,∠A=∠B, △AOD△BOC全等吗?
为什么?两角和夹边对应相等(已知)(对顶角相等)解:∵点O是AB的中点(已知)∴AO=BO(中点定义)(已证)≌1、 图中的两个三角形全等吗? 请说明理由.解:两个三角形全等.ABCD(已知)(已知)(公共边)=35°=110°练一练∵2、如图,点B,F,C,E在同一条直线上,∠B=
∠E,∠1=∠2,BF=EC.△ABC与△DEF全等
吗?为什么?解: △ABC≌△DEF ∵ BF=EC,FC=CF(已知)
∴ BF+FC=EC+CF(等式的基本性质)
即 BC=EF在△ABC和△DEF中,
∠1=∠2(已知)
BC=EF(已证)
∠B=∠E(已知)
∴ △ABC≌△DEF (ASA) 例2:如图,在△ABC中,AD是中线,
BE⊥AD于点E,CF⊥AD于点F,BE与CF相
等吗? 如图,OP是∠MON的角平分线,C是OP上的一点,CA⊥OM,CB⊥ON,垂足分别为A、B,△AOC与△BOC全等吗?为什么?AB.C例3:ABMNP 1、如果改变点C在OP上的位置,那么 △AOC与△BOC仍然全等吗?CA与CB有什么数量关系?BNP.C B议一议分析: △AOC≌△BOC,
CA=CB
∵ △AOC≌△BOC
∴ CA=CB
( ) 全等三角形的对应边相等CACO两角夹一边 (ASA)两角及其中一角的对边(AAS)两角及一边两边及夹角 (SAS)1 判别三角形全等的三个条件:小结 2 找三角形全等条件时,注意题目中的间接条件和图形中的隐含条件的正确使用.3 掌握证明三角形全等的规范格式;注意每步要有推理的依据。1. 如图 △ABC的角平分线AD、BE相交于点P.分别画出点P到边AB、BC、CA的垂线段PF、PG、PH,这3条线段相等吗? 为什么?解: 如图PF、PG、PH即为所求.PF=PG=PH ∵ P在△ABC的角平分线AD上
PF⊥AB,PH⊥AC(已知)
∴PF=PH(角平分线上的点到 角的两边距离相等)同理可得: PF=PG∴ PF=PG=PH(等量代换)2、如图,∠ABC的平分线与△ABC的外角∠ACD的平分线相交于点M。试画出点M到△ABC三边所在直线的垂线段。这三条垂线段的长度相等吗?为什么?NPQ解: 如图MP、MQ、MN即为所求作.MP=MQ=MN ∵ M是角平分线BM上一点,
且 MP⊥BA, MN⊥BC,
∴MP=MN(角平分线上的 点到角的两边距离相等)同理可得: MN=MQ∴ MP = MN = MQ(等量代换)○○××角平分线的性质:
角平分线上的点到角的两边的距离相等.ABONP.C B2、你能发现什么结论?∵ C是∠MON的角平分线OP上一点且 CA⊥OM于点A,CB⊥ON于点B∴ CA=CBC几何语言:(角平分线上的点到角的两边的距离相等.)(已知)
三角形全等的条件
(4)
三边对应相等的两个三角形全等,简写成 “边边边” 或 “SSS”在△ABC和△DEF中,
AB=DE(已知)
AC=DF(已知)
BC=EF(已知)
∴ △ABC≌△DEF (SSS) 几何语言:1 判定两个三角形全等必须具备三个条件:两边和它们的夹角(SAS)两角和它们的夹边(ASA)两角和其中一角的对边(AAS)三边 (SSS)回顾:2 找三角形全等条件时,
(1)常借助于图中的隐含条件.“ 对顶角相等,公共角,公共边 ”(2)先把图中的间接条件转化为直接条件。想一想:利用角尺平分一个任意角。如图 OA=OB,移动角尺,使角尺两边相同的刻度分别与点A、B重合,这时过角尺顶点M的射线OM就是∠COD的平分线。为什么?解:
∵ 在△ABC和△FED中,
OA=OB(已知)
OM=OM(公共边)
AM=BM(已知)
∴ △AOM≌△BOM (SSS)
∴∠AOM=∠BOM(全等三角形的对应角相等)
∴射线OM就是∠COD的角平分线。想一想: 用尺和圆规作一个角的平分线。如图,这时过角尺顶点M的射线OM就是∠AOB的平分线。为什么?OABC【例1】如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,AD=FC,∠B与∠E相等吗?为什么?解: ∠B=∠E∵ AD=FC(已知)
∴ AD-CD=FC-DC 即AC=FD ∴在△ABC和△FED中,
AB=FE(已知)
AC=FD(已证)
BC=ED(已知)
∴ △ABC≌△FED (SSS) ∴ ∠B=∠E(全等三角形的对应角相等)【变式】如图,点A、C、D、F在同一条直线上, ∠BCD= ∠CDE,BC=ED,AD=FC,线段AB与线段FE有怎样的关系?为什么?练一练:1、如图,△ABC中,AB=AC,AD是BC边上的中线,则∠BDA= 度,为什么?
90AD是△ABC的角平分线,为什么?例2: 如图, ,
AD、A1D1分别是△ABC和△A1B1C1的高,你能说明AD=A1D1吗? 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连接DC。(1)请找出图2中的全等三角形,并给予说明。
例3:图1图2 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连接DC。(2)说明:DC⊥BE
例3:图1图2 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于点D,BE⊥MN于点E。
(1)当直线MN
绕点C旋转到图①
的位置时,
DE=AD+BE吗?
说明理由。【例4】① 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于点D,BE⊥MN于点E。
(2)说明当直线
MN绕点C旋转到
图②的位置时,
DE=AD?BE。【例4】 ② 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于点D,BE⊥MN于点E。
(3)当直线MN
绕点C旋转到图③
的位置时,DE、
AD、BE具有怎样
的位置关系?【例4】③1 判定两个三角形全等必须具备三个条件:两边和它们的夹角(SAS)两角和它们的夹边(ASA)两角和其中一角的对边(AAS)三边 (SSS)回顾:2 找三角形全等条件时,
(1)常借助于图中的隐含条件.“ 对顶角相等,公共角,公共边 ”(2)先把图中的间接条件转化为间接条件。 直角三角形全等
的条件(5)
按下列要求作图。
1 画 ∠PCQ=90°, 2 在射线CP上取CB=3cm, 3 以B为圆心,5cm为半径画弧 交射线CQ于点A, 4 连接AB, △ABC为所求。尺规作图DCEBA 直角△ABC
记作:Rt△ABC 将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?直角三角形全等的条件 斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”.几何语言: 你现在能够用几种方法说明两个直角三角形全等? 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:
SAS、ASA、AAS、SSS,
还有直角三角形特殊的判定方法 —“HL”.三角形全等的条件(6) 习题课【例1】 如图,AB=AE,BC=ED,∠ABC=∠AED,点F是CD的中点,猜想线段AF和CD有怎样的位置关系?为什么?【例2】 如图,AD∥BC,AD=BC,
AE⊥AD,AF⊥AB,且AE=AD,AF=
AB,AC与EF是否相等?为什么?P AC与EF有什么位置关系?延长CA交EF于点P【例3】 如图,正方形ABCD的对角线相交于点O,点O是正方形A`B`C`O的一个顶点,如果两个正方形的边长均为a,
那么正方形A`B`C`O绕点O无
论怎么转动,两个正方形
的重叠部分(即阴影部分)
的面积,总等于一个定值。
猜想一下,这个定值是多少?
为什么?【例4】 如图,已知BE、CF是△ABC
的高,且BP=AC,CQ=AB,则AP与AQ
有什么关系?为什么?数量关系位置关系关系【例5】 如图,已 知
DC∥AB,∠BAD和∠ADC
的平分线相交于点E,过
点E的直线分别交DC、
AB于点C、B两点,试
说明AD=AB+CD。 【例6】 如图,已知AC
⊥BC,AC=10,BC=5,
AD⊥AC,点P、Q分别为
AC、AD 上的动点,当AP
为何值时△ABC与△APQ
全等?
相等。
2、如图1,已知△AOC≌△BOD,
则∠A=∠B,∠C= ,
=∠2,
对应边有AC= , =OB,
=OD。对应边对应角∠D∠1BDOAOC全等三角形的对应边相等,对应角相等。我们知道: 反过来,判别两个三角形全等需要哪些条件? 即它们有多少组边或角分别相等时就全等?寻求: 判别三角形全等的条件.只给一个条件(一条边或一个角)只给一条边时:
如:3cm3cm3cm只给一个角时
如:45°45°45° 如果三角形的一条边为3cm,一个内角为30°3cm3cm3cm30°30°30°给出两个条件时(一边及一角)给出两个条件时(已知两角)如果三角形两个内角分别为30°,45°时30°45°给出两个条件时(已知两边)如果三角形的两边分别为4cm,6cm 时6cm4cm4cm三角形全等的条件两边一角对应相等两边夹角对应相等
(边角边) 两边一对角对应相等
(边边角)交流与讨论1、如图,每人用一张长方形纸剪一个直角三角形,怎样剪才能使剪下的所有直角三角形都能够重合?交流与讨论2、在下图中, △ABC与△DEF、△MNP能完全重合吗?3、大家一起做下面的实验1:用尺规作△ABC,使∠A=60°,AB=3cm,AC=4cm. (1)画∠MAN= 60° ;
(2)在AM、 AN上分别截取AB=3cm,
AC=4cm;
(3)连接BC。
△ABC就是所求作的三角形.CB′做一做与周围同学所画的比较一下,它们全等吗?课本P13α作法:结论:两边及其中一边所对的角对应相等,两个三角形不一定全等. 先画一个45°的角,然后在其中一边上取3.5厘米,最后画45°的角所对的边2.5厘米。4、大家一起做下面的实验2:两边一角对应相等两边夹角对应相等
(边角边) 两边一对角对应相等
(边边角)(×)(√)再次明确实践告诉我们判定两个三角形全等的一个基本事实:两边及其夹角分别相等的两个三角形全等(可简写为“边角边”或“SAS”)在△ABC和△ DEF中,
AB = DE
∠B =∠E
BC = EF
∴ △ABC≌△DEF (SAS) 几何语言:两边及其夹角分别相等的两个三角形全等(可简写为“边角边”或“SAS”)已知:如图, AB=AD ,∠BAC=∠DAC
求证:△ABC≌△ADC .解:AB=AD (已知)∠BAC=∠DAC (已知)AC=AC(公共边)∵ 在△ABC 和△ADC中∴ △ABC ≌△ADC (SAS)注意:1、 要充分利用图形中“公共边”这个条件.
2、 △ABC沿直线AC翻折后能够与△ADC重合.归纳:判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。 现在例1的已知条件不改变, 而问题改变成: “DC与BC相等吗”, 如何作答?……
∴ △ABC ≌△ADC (SAS)
∴ DC=BC (全等三角形的对应边相等)证明三角形全等的步骤:?1.写出在哪两个三角形中证明全等。(注意把表示对应顶点的字母写在对应的位置上).
?2.按边、角、边的顺序列出三个条件,用大括号合在一起.
?3.写出结论.每步要有推理的依据.1、在下列三角形中,哪两个三角形全等?40°4430°444640°⑴⑵⑶⑷⑸⑹解: 全等的三角形有:⑴和⑷, ⑶和⑸.P14练一练:课堂练习2、已知:如图,AB=AC,点D、E分别在AB、AC上,且AD=AE.
求证:△ABE≌△ACD.注意: 要充分利用图形中“公共角”这个条件.你还能得到哪些相等的线段?说明理由.3、已知:如图,AC与BD相交于点O,且OA=OC,OB=OD,
求证:△AOB≌△COD注意: 要充分利用图形中“对顶角相等”这个条件. 小结:1 两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”2 两边以及其中一边的对角对应相等的两个三角形不一定全等.注意: 要充分利用图形中 “对顶角,公共角,公共边”这些条件.3 判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。1.3探索三角形全等的条件(2)习题课∵在△ABC和△ DEF中,
AB = DE
∠B =∠E
BC = EF
∴ △ABC≌△DEF (SAS) 几何语言:两边及其夹角分别相等的两个三角形全等(可简写为“边角边”或“SAS”)复习回顾例1、判断题:
(1)有2条边对应相等的2个三角形全等。( )
(2)有两边和1个角对应相等的2个三角形全等。( )
(3)2条直角边对应相等的2个直角三角形全等。( )
(4)边长相等的2个等边三角形全等。( ) √××√例题精讲已知:如图,AB、CD相交于点E,且点E是AB、CD的中点.
求证:△AEC≌△BED例题精讲例2思考:你能说明图中的AC∥DB吗?注意:△AEC绕点E旋转180°后可以与△BED重合。已知:如图,点E、F在CD上,且CE=DF,AE=BF,AE∥BF.
求证:△AEC≌△BFD例题精讲例3思考:
1、能够改变例3中△AEC的位置得到例2 的图形?
2、根据例3中的已知条件,你还能得到那些结论?1、课本P16 练习1、2、3
2、课本P29习题1.3 1、3
(作业:4、5给予提示)
课堂练习课本P29 习题1.33、如图,把两根钢条AA’、BB’的中点O连在一起,可以做成一个测量工件内槽宽的工具(这种工具叫做卡钳),只要量出A′B′的长度,就可以知道工件内径AB的长度是否符合标准。你能说出这样测量的理由吗? 先做P29第1题1、已知:如图,AD=AE,BD=CE,∠ADE=∠AED,
求证:△ADB≌△AEC. 思考:
若将条件“BD=CE”改成“BE=CD”能得到同样的结论吗?2、已知:如图,MP=MQ,MN=MG,
∠PMN=∠QMG.
求: 请在图中找出全等三角形,并说明理由。课堂小结通过本节课你学到了哪些知识?说一说你的收获吧!布置作业1、上本子:P30习题1.3 4、5
2、《评价手册》
3、《补充习题》三角形全等的条件(3)两角夹一边 ?两角及其中一角的对边 ?两角及一边两边及夹角 (SAS)判别三角形全等的三个条件:(已知两角及夹边)做一做 两角和它们的夹边对应相等的两个三角形全等.
简写成:“角边角”或“ASA”见书p17讨论 两角和它们的夹边对应相等的两个三角形全等.
简写成:“角边角”或“ASA”在△ABC和△ MNP中,
∠B =∠N
BC = NP
∠C=∠P
∴ △ABC≌△MNP (ASA) 几何语言:(已知两角和其中一角的对边)如图,在△ABC与△MNP中,∠A=∠M,∠B=∠N,BC=NP,△ABC与△MNP全等吗?为什么?想一想这里能将以上条件转化成“ASA”证明吗? 两角和其中一角的对边对应相等的两个三角形全等. 简写成:“角角边”或“AAS”几何语言:两角夹一边 (ASA)两角及其中一角的对边(AAS)两角及一边两边及夹角 (SAS)判别三角形全等的三个条件: (1) 如图,小明不慎将一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃吗? 如果可以,带哪块去合适? 你能说明其中理由吗?议一议①②两角和它们的夹边对应相等的两个三角形全等.○①②( )∵在 中例1: 如图,O是AB的中点,∠A=∠B, △AOD△BOC全等吗?
为什么?两角和夹边对应相等(已知)(对顶角相等)解:∵点O是AB的中点(已知)∴AO=BO(中点定义)(已证)≌1、 图中的两个三角形全等吗? 请说明理由.解:两个三角形全等.ABCD(已知)(已知)(公共边)=35°=110°练一练∵2、如图,点B,F,C,E在同一条直线上,∠B=
∠E,∠1=∠2,BF=EC.△ABC与△DEF全等
吗?为什么?解: △ABC≌△DEF ∵ BF=EC,FC=CF(已知)
∴ BF+FC=EC+CF(等式的基本性质)
即 BC=EF在△ABC和△DEF中,
∠1=∠2(已知)
BC=EF(已证)
∠B=∠E(已知)
∴ △ABC≌△DEF (ASA) 例2:如图,在△ABC中,AD是中线,
BE⊥AD于点E,CF⊥AD于点F,BE与CF相
等吗? 如图,OP是∠MON的角平分线,C是OP上的一点,CA⊥OM,CB⊥ON,垂足分别为A、B,△AOC与△BOC全等吗?为什么?AB.C例3:ABMNP 1、如果改变点C在OP上的位置,那么 △AOC与△BOC仍然全等吗?CA与CB有什么数量关系?BNP.C B议一议分析: △AOC≌△BOC,
CA=CB
∵ △AOC≌△BOC
∴ CA=CB
( ) 全等三角形的对应边相等CACO两角夹一边 (ASA)两角及其中一角的对边(AAS)两角及一边两边及夹角 (SAS)1 判别三角形全等的三个条件:小结 2 找三角形全等条件时,注意题目中的间接条件和图形中的隐含条件的正确使用.3 掌握证明三角形全等的规范格式;注意每步要有推理的依据。1. 如图 △ABC的角平分线AD、BE相交于点P.分别画出点P到边AB、BC、CA的垂线段PF、PG、PH,这3条线段相等吗? 为什么?解: 如图PF、PG、PH即为所求.PF=PG=PH ∵ P在△ABC的角平分线AD上
PF⊥AB,PH⊥AC(已知)
∴PF=PH(角平分线上的点到 角的两边距离相等)同理可得: PF=PG∴ PF=PG=PH(等量代换)2、如图,∠ABC的平分线与△ABC的外角∠ACD的平分线相交于点M。试画出点M到△ABC三边所在直线的垂线段。这三条垂线段的长度相等吗?为什么?NPQ解: 如图MP、MQ、MN即为所求作.MP=MQ=MN ∵ M是角平分线BM上一点,
且 MP⊥BA, MN⊥BC,
∴MP=MN(角平分线上的 点到角的两边距离相等)同理可得: MN=MQ∴ MP = MN = MQ(等量代换)○○××角平分线的性质:
角平分线上的点到角的两边的距离相等.ABONP.C B2、你能发现什么结论?∵ C是∠MON的角平分线OP上一点且 CA⊥OM于点A,CB⊥ON于点B∴ CA=CBC几何语言:(角平分线上的点到角的两边的距离相等.)(已知)
三角形全等的条件
(4)
三边对应相等的两个三角形全等,简写成 “边边边” 或 “SSS”在△ABC和△DEF中,
AB=DE(已知)
AC=DF(已知)
BC=EF(已知)
∴ △ABC≌△DEF (SSS) 几何语言:1 判定两个三角形全等必须具备三个条件:两边和它们的夹角(SAS)两角和它们的夹边(ASA)两角和其中一角的对边(AAS)三边 (SSS)回顾:2 找三角形全等条件时,
(1)常借助于图中的隐含条件.“ 对顶角相等,公共角,公共边 ”(2)先把图中的间接条件转化为直接条件。想一想:利用角尺平分一个任意角。如图 OA=OB,移动角尺,使角尺两边相同的刻度分别与点A、B重合,这时过角尺顶点M的射线OM就是∠COD的平分线。为什么?解:
∵ 在△ABC和△FED中,
OA=OB(已知)
OM=OM(公共边)
AM=BM(已知)
∴ △AOM≌△BOM (SSS)
∴∠AOM=∠BOM(全等三角形的对应角相等)
∴射线OM就是∠COD的角平分线。想一想: 用尺和圆规作一个角的平分线。如图,这时过角尺顶点M的射线OM就是∠AOB的平分线。为什么?OABC【例1】如图,点A、C、D、F在同一条直线上,AB=FE,BC=ED,AD=FC,∠B与∠E相等吗?为什么?解: ∠B=∠E∵ AD=FC(已知)
∴ AD-CD=FC-DC 即AC=FD ∴在△ABC和△FED中,
AB=FE(已知)
AC=FD(已证)
BC=ED(已知)
∴ △ABC≌△FED (SSS) ∴ ∠B=∠E(全等三角形的对应角相等)【变式】如图,点A、C、D、F在同一条直线上, ∠BCD= ∠CDE,BC=ED,AD=FC,线段AB与线段FE有怎样的关系?为什么?练一练:1、如图,△ABC中,AB=AC,AD是BC边上的中线,则∠BDA= 度,为什么?
90AD是△ABC的角平分线,为什么?例2: 如图, ,
AD、A1D1分别是△ABC和△A1B1C1的高,你能说明AD=A1D1吗? 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连接DC。(1)请找出图2中的全等三角形,并给予说明。
例3:图1图2 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连接DC。(2)说明:DC⊥BE
例3:图1图2 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于点D,BE⊥MN于点E。
(1)当直线MN
绕点C旋转到图①
的位置时,
DE=AD+BE吗?
说明理由。【例4】① 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于点D,BE⊥MN于点E。
(2)说明当直线
MN绕点C旋转到
图②的位置时,
DE=AD?BE。【例4】 ② 在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于点D,BE⊥MN于点E。
(3)当直线MN
绕点C旋转到图③
的位置时,DE、
AD、BE具有怎样
的位置关系?【例4】③1 判定两个三角形全等必须具备三个条件:两边和它们的夹角(SAS)两角和它们的夹边(ASA)两角和其中一角的对边(AAS)三边 (SSS)回顾:2 找三角形全等条件时,
(1)常借助于图中的隐含条件.“ 对顶角相等,公共角,公共边 ”(2)先把图中的间接条件转化为间接条件。 直角三角形全等
的条件(5)
按下列要求作图。
1 画 ∠PCQ=90°, 2 在射线CP上取CB=3cm, 3 以B为圆心,5cm为半径画弧 交射线CQ于点A, 4 连接AB, △ABC为所求。尺规作图DCEBA 直角△ABC
记作:Rt△ABC 将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?直角三角形全等的条件 斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”.几何语言: 你现在能够用几种方法说明两个直角三角形全等? 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:
SAS、ASA、AAS、SSS,
还有直角三角形特殊的判定方法 —“HL”.三角形全等的条件(6) 习题课【例1】 如图,AB=AE,BC=ED,∠ABC=∠AED,点F是CD的中点,猜想线段AF和CD有怎样的位置关系?为什么?【例2】 如图,AD∥BC,AD=BC,
AE⊥AD,AF⊥AB,且AE=AD,AF=
AB,AC与EF是否相等?为什么?P AC与EF有什么位置关系?延长CA交EF于点P【例3】 如图,正方形ABCD的对角线相交于点O,点O是正方形A`B`C`O的一个顶点,如果两个正方形的边长均为a,
那么正方形A`B`C`O绕点O无
论怎么转动,两个正方形
的重叠部分(即阴影部分)
的面积,总等于一个定值。
猜想一下,这个定值是多少?
为什么?【例4】 如图,已知BE、CF是△ABC
的高,且BP=AC,CQ=AB,则AP与AQ
有什么关系?为什么?数量关系位置关系关系【例5】 如图,已 知
DC∥AB,∠BAD和∠ADC
的平分线相交于点E,过
点E的直线分别交DC、
AB于点C、B两点,试
说明AD=AB+CD。 【例6】 如图,已知AC
⊥BC,AC=10,BC=5,
AD⊥AC,点P、Q分别为
AC、AD 上的动点,当AP
为何值时△ABC与△APQ
全等?
