柱锥台球的体积推导全过程
图片预览




文档简介
课件14张PPT。1.1.7柱、锥、台和球的体积几何体占有空间部分的大小叫做它的体积一、复习巩固:1、体积的概念:从小学到初中
你学过哪些几何体的体积公式?
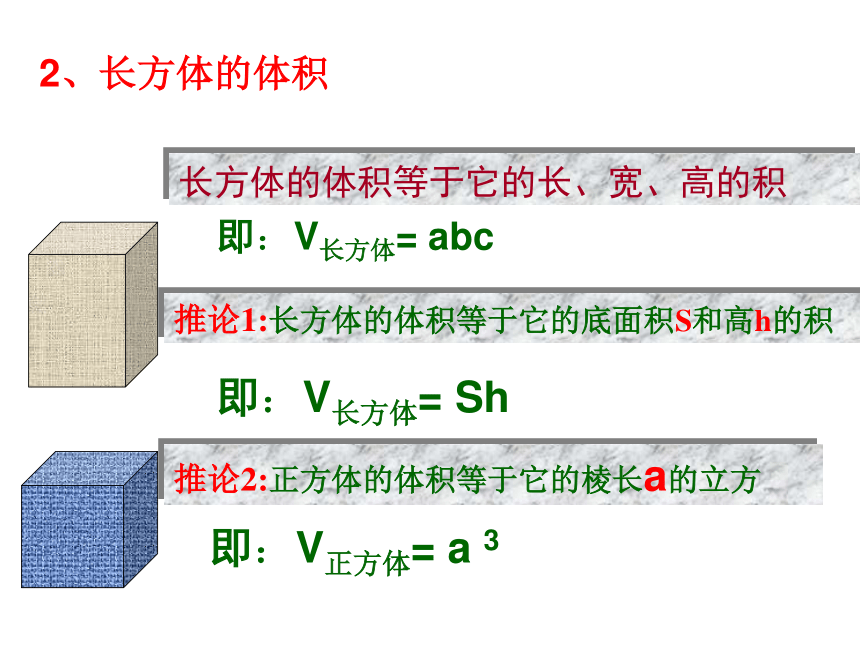
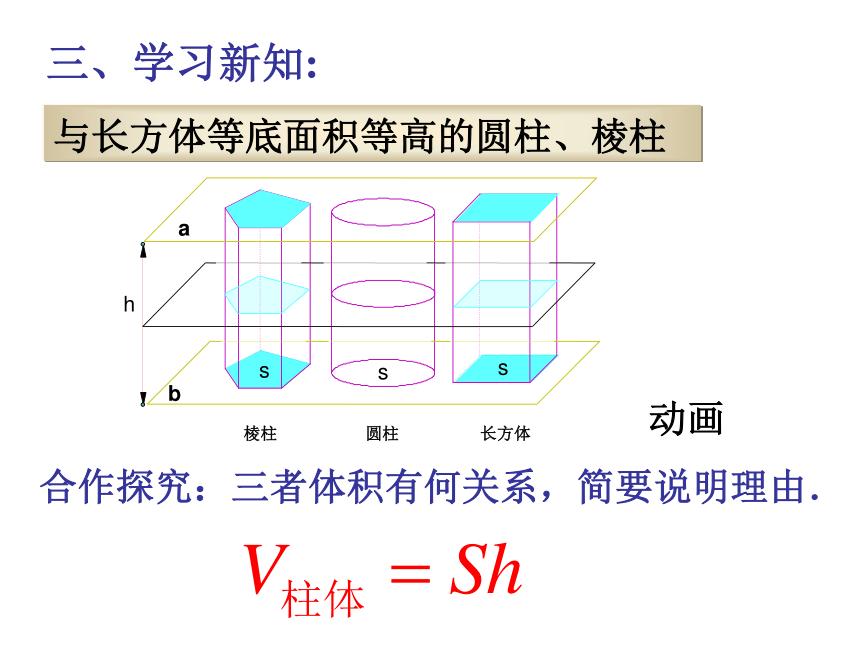
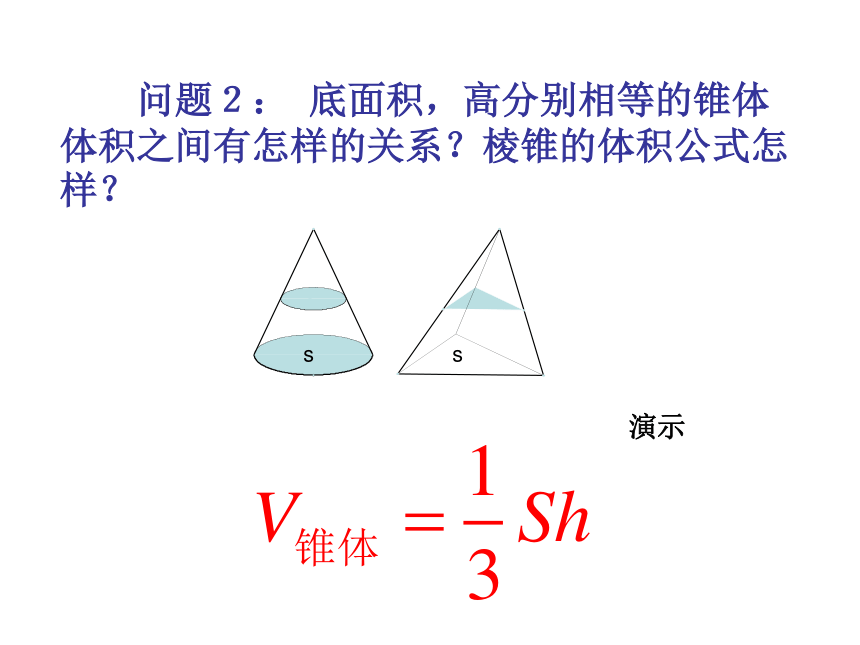
还记得吗?长方体的体积等于它的长、宽、高的积即:V长方体= abc即:V长方体= Sh即:V正方体= a 3推论2:正方体的体积等于它的棱长a的立方推论1:长方体的体积等于它的底面积S和高h的积2、长方体的体积二、讲授新课: 取一摞书放在桌面上,并改变它们的形状,观察改变前后的体积是否发生变化? 两等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.祖暅原理:三、学习新知:长方体圆柱棱柱与长方体等底面积等高的圆柱、棱柱sss合作探究:三者体积有何关系,简要说明理由. 动画 问题2: 底面积,高分别相等的锥体体积之间有怎样的关系?棱锥的体积公式怎样? ss演示 台体与锥体之间的联系如何?ssxhsss 合作探究:观察柱、锥、台的联系,指出三者体积公式的联系实践感悟:结论:倒米实验:将一个底面半径和高都为R的圆锥放入一个底面
半径和高都为R的圆柱内,使圆锥的底和圆柱的
底重合,并给这个模型内装满米,然后把这个模
型中的米全倒进半径为R的半球内,你会发现……. =演示例1、如图所示,在长方体ABCD-A‘B’C‘D’中,用截面截下一个棱锥C-A’DD’,求棱锥C-A‘DD’的体积与剩余部分的体积之比。 若球的半径变为原来的2倍,则表面积变为
原来的_______倍,体积变为原来的_______倍. 若两球表面积之比为1:2,则其体积之比是
_______.48例: 有一堆相同规格的六角螺帽毛坯共重5.8kg. 已知底面六边形的边长是12mm,高是10mm,内孔直径是10mm. 问约有毛坯多少个?(铁的比重是7.8g/cm3)解:六角螺帽的体积是一个正六棱柱的体积与一个圆柱的体积的差。一个毛坯的体积为答:共251个.四、数学运用:练习:
1、已知一个铜质的五棱柱的底面积为16平方厘米,高为4厘米,现将它融化后铸成一个正方体的铜块,那么铸成的铜块的棱长为多少?2、某一沙堆是一正四棱锥形,测得底面边长为2米,侧棱长为3米,那么这个沙堆的体积是多少? 变式:过各侧棱中点的平面与棱锥相交所得的截面与底面之间的部分是一个正四棱台,求此四棱台的体积.
你学过哪些几何体的体积公式?
还记得吗?长方体的体积等于它的长、宽、高的积即:V长方体= abc即:V长方体= Sh即:V正方体= a 3推论2:正方体的体积等于它的棱长a的立方推论1:长方体的体积等于它的底面积S和高h的积2、长方体的体积二、讲授新课: 取一摞书放在桌面上,并改变它们的形状,观察改变前后的体积是否发生变化? 两等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.祖暅原理:三、学习新知:长方体圆柱棱柱与长方体等底面积等高的圆柱、棱柱sss合作探究:三者体积有何关系,简要说明理由. 动画 问题2: 底面积,高分别相等的锥体体积之间有怎样的关系?棱锥的体积公式怎样? ss演示 台体与锥体之间的联系如何?ssxhsss 合作探究:观察柱、锥、台的联系,指出三者体积公式的联系实践感悟:结论:倒米实验:将一个底面半径和高都为R的圆锥放入一个底面
半径和高都为R的圆柱内,使圆锥的底和圆柱的
底重合,并给这个模型内装满米,然后把这个模
型中的米全倒进半径为R的半球内,你会发现……. =演示例1、如图所示,在长方体ABCD-A‘B’C‘D’中,用截面截下一个棱锥C-A’DD’,求棱锥C-A‘DD’的体积与剩余部分的体积之比。 若球的半径变为原来的2倍,则表面积变为
原来的_______倍,体积变为原来的_______倍. 若两球表面积之比为1:2,则其体积之比是
_______.48例: 有一堆相同规格的六角螺帽毛坯共重5.8kg. 已知底面六边形的边长是12mm,高是10mm,内孔直径是10mm. 问约有毛坯多少个?(铁的比重是7.8g/cm3)解:六角螺帽的体积是一个正六棱柱的体积与一个圆柱的体积的差。一个毛坯的体积为答:共251个.四、数学运用:练习:
1、已知一个铜质的五棱柱的底面积为16平方厘米,高为4厘米,现将它融化后铸成一个正方体的铜块,那么铸成的铜块的棱长为多少?2、某一沙堆是一正四棱锥形,测得底面边长为2米,侧棱长为3米,那么这个沙堆的体积是多少? 变式:过各侧棱中点的平面与棱锥相交所得的截面与底面之间的部分是一个正四棱台,求此四棱台的体积.
