最新人教版八年级数学下册19.2.2一次函数3课件
文档属性
| 名称 | 最新人教版八年级数学下册19.2.2一次函数3课件 |  | |
| 格式 | zip | ||
| 文件大小 | 345.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-30 14:33:56 | ||
图片预览





文档简介
课件29张PPT。人教版八年级(下册)第十九章一次函数19.2.2一次函数
(第3课时)高于铺二中 张涛1.学会用待定系数法求一次函数解析式;
2.了解分段函数的表示及其图象;能初步应用一次函数模型解决现实生活中的问题,体会一次函数的应用价值.
学习重点:
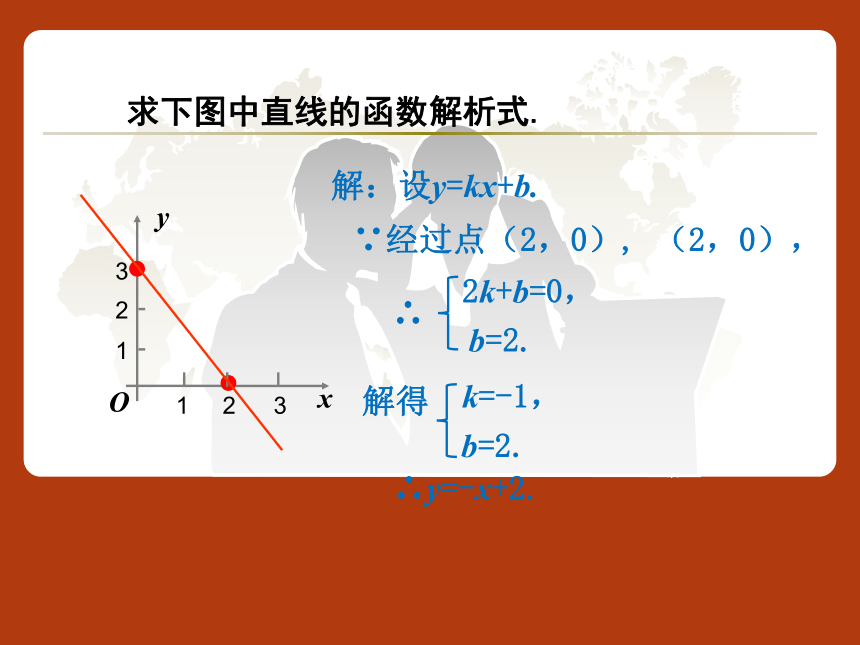
用待定系数法求一次函数解析式,初步了解分段函数.学习目标:1.画出函数y= x与y=3x-1的图象. 2.你在画这两个函数图象时,分别描了几个点?你为何选取这几个点?可以有不同取法吗?一、复习与反思求下图中直线的函数解析式.二、提出问题,形成思路O2x12-2-11解:设y=kx.∵经过点(1,2),∴ k=2.∴y=2x.y求下图中直线的函数解析式.O1xy12332解:设y=kx+b.∵经过点(2,0), (2,0), 2k+b=0,∴y=-x+2.b=2.解得k=-1,b=2.∴反思小结: 确定正比例函数的解析式需要一个条件,确定一次函数的解析式需要两个条件. 已知一次函数的图象过点 (3,5) 与 (-4,-9),
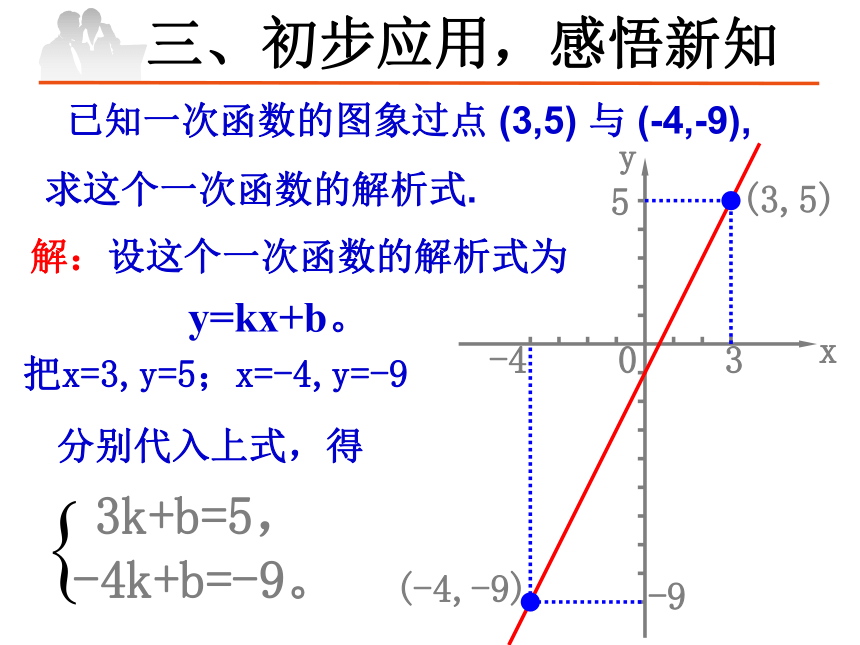
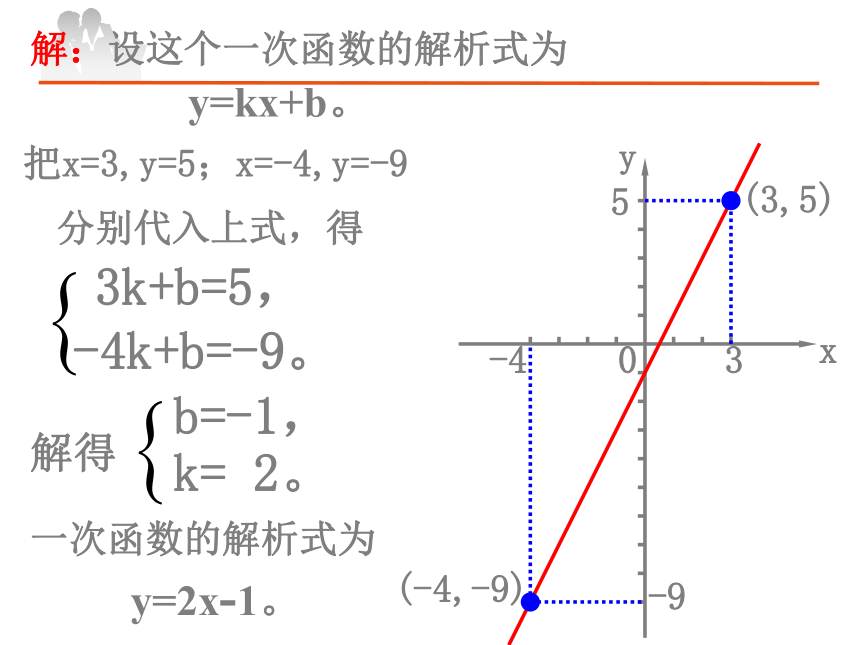
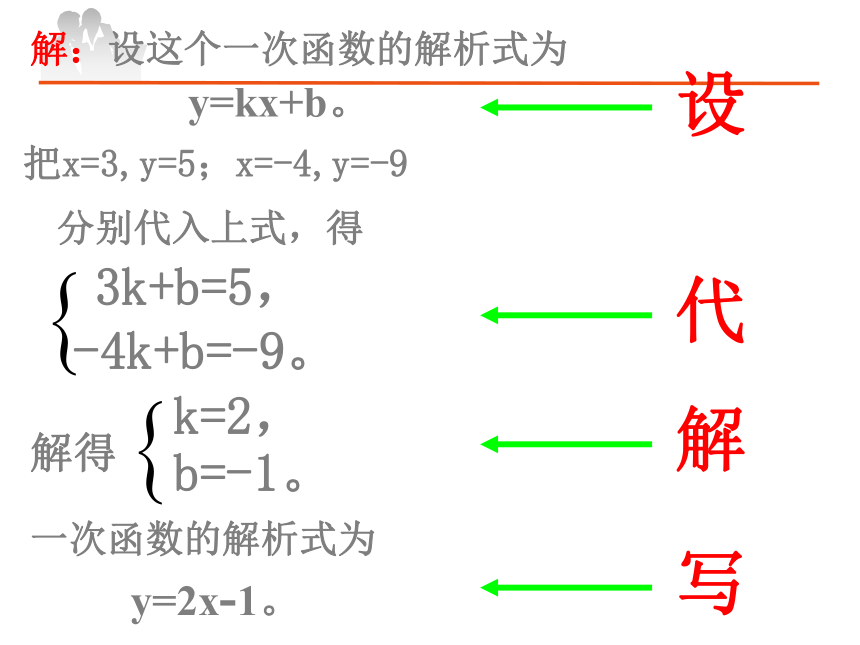
求这个一次函数的解析式.35-4-9解:设这个一次函数的解析式为y=kx+b。把x=3,y=5;x=-4,y=-93k+b=5, 分别代入上式,得-4k+b=-9。三、初步应用,感悟新知解:设这个一次函数的解析式为y=kx+b。把x=3,y=5;x=-4,y=-93k+b=5, 分别代入上式,得-4k+b=-9。解得b=-1,k= 2。一次函数的解析式为y=2x-1。解:设这个一次函数的解析式为y=kx+b。把x=3,y=5;x=-4,y=-93k+b=5, 分别代入上式,得-4k+b=-9。解得一次函数的解析式为y=2x-1。设代解写 像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法. 在前面的学习过程中我们发现数与形之间是怎样结合互化的?函数解析式y=kx+b一次函数的图象直线l满足条件的两定点(x1,y1)(x2,y2)解出选取选取解出解题的四个步骤:第一步:设,设出函数的一般形式。(称一次函数的通式)第二步:代,代入解析式得出方程或方程组。第三步:解,通过列方程或方程组解出待定系数k,b的值。第四步:写,写出该函数的解析式。整理归纳从数到形从形到数数学的基本思想方法:数形结合练习:
(1)已知一次函数的图象经过点(1,-1)和点(-1,2)。求这个函数的解析式。
(2)已知一次函数y=kx+b中,当x=1时,y=3,当x=-1时,y=7。求这个函数的解析式。且求当x=3时,y的值。
(3)师:已知直线上两点坐标,能求出这条直线的解析式,若不直接告诉两点的坐标,已知这条直线的图象,能否求出它的解析式?
如:
1)已知一次函数的图象经过点(1,-1)和点(-1,2)。求这个函数的解析式。
解:设这个一次函数的解析式为y=kx+b。
把x=1,y=-1;x=-1,y=2,分别代入上式,得
﹛K+b=-1,
-k+b=2。
解得﹛K= ,b= 。一次函数的解析式为y= x 。(2)解:把x=1,y=3;x=-1,y=7,分别代入y=kx+b,得
﹛K+b=3,-k+b=7。解得﹛K=-2,b=5。一次函数的解析式为y=-2x+5。
当x=3时 ,y=-1。(3)由题意已知一次函数的图象经过点(2,0)和点(0,-3),设这个一次函数的解析为y=kx+b。
把x=2,y=0;x=0,y=-3分别代入上式,得
﹛2k+b=0,b=-3。解得﹛K= ,b=-3。一次函数的解析式为y= x-3。一次函数图像经过点(9,0)和点(24,20),写出函数解析式.解:练一练 设这个一次函数的解析式为y=kx+b.把点(9,0)与(24,20)分别代入y=kx+b,得:
已知一次函数的图象经过点(-4,9)和点(6,3),求这个函数的解析式.
解: 设这个一次函数的解析式为y=kx+b.把点(-4,9)与(6,3)分别代入y=kx+b,得:
练一练1、选择题CADD尝试练习3.一次函数y=kx+5与直线y=2x-1交于点P(2,m),求k、m的值.4.一次函数y=3x-b过A(-2,1)则b= ,该图象经过点B( ,-1)和点C(0, ).5.已知函数y=kx+b的图象与另一个一次函数y=-2x-1的图象相交于y轴上的点A,且x轴下方的一点B(3,n)在一次函数y=kx+b的图象上,n满足关系n2=9.求这个函数的解析式. 1.写出两个一次函数,使它们的图象都经过点(-2,3). 2.生物学家研究表明,某种蛇的长度y(cm)是其尾长x(cm)的一次函数,当蛇的尾长为6 cm时,蛇长为45.5 cm;当尾长为14 cm时,蛇长为105.5 cm.当蛇的尾长为10 cm时,这条蛇的长度是多少?四、综合应用y=7.5x+0.575.5 cm 3.一个函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,-3a)与点(a,6),求这个函数的解析式. 4.小明将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数x(月)之间的关系如图所示,根据下图回答下列问题: (1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经过几个月才能存够200元?O40xy123120804y=20x+408个月1.用待定系数法求函数解析式的一般步骤.2.数形结合解决问题的一般思路.五、回顾反思1.必做题:
教材第95页练习第1题,第99页习题19.2第6、7题.六、作业2.备选题: (1)若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过( )
A.A(-1,1) B.B(2,2)
C.C(-2,2) D.D(2,-2)
(2)老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质:
甲:函数的图象经过第一象限;
乙:函数的图象经过第二象限;
丙:在每个象限内,y随x的增大而减小.
请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数解析式: .
C (3)如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据: ①求出h与d之间的函数解析式(不要求写出自变量d的取值范围).
②某人身高为196 cm,一般情况下他的指距应是多少?解:(1)设h与d之间的函数关系式为:
h=kd+b. 把d=20,h=160,d=21,h=169,
分别代入得,
20k+b=160,
21k+b=169. 解得k=9,b=-20,
即h=9d-20. (2)当h=196时,196=9d-20,解得d=24(cm).再见!
(第3课时)高于铺二中 张涛1.学会用待定系数法求一次函数解析式;
2.了解分段函数的表示及其图象;能初步应用一次函数模型解决现实生活中的问题,体会一次函数的应用价值.
学习重点:
用待定系数法求一次函数解析式,初步了解分段函数.学习目标:1.画出函数y= x与y=3x-1的图象. 2.你在画这两个函数图象时,分别描了几个点?你为何选取这几个点?可以有不同取法吗?一、复习与反思求下图中直线的函数解析式.二、提出问题,形成思路O2x12-2-11解:设y=kx.∵经过点(1,2),∴ k=2.∴y=2x.y求下图中直线的函数解析式.O1xy12332解:设y=kx+b.∵经过点(2,0), (2,0), 2k+b=0,∴y=-x+2.b=2.解得k=-1,b=2.∴反思小结: 确定正比例函数的解析式需要一个条件,确定一次函数的解析式需要两个条件. 已知一次函数的图象过点 (3,5) 与 (-4,-9),
求这个一次函数的解析式.35-4-9解:设这个一次函数的解析式为y=kx+b。把x=3,y=5;x=-4,y=-93k+b=5, 分别代入上式,得-4k+b=-9。三、初步应用,感悟新知解:设这个一次函数的解析式为y=kx+b。把x=3,y=5;x=-4,y=-93k+b=5, 分别代入上式,得-4k+b=-9。解得b=-1,k= 2。一次函数的解析式为y=2x-1。解:设这个一次函数的解析式为y=kx+b。把x=3,y=5;x=-4,y=-93k+b=5, 分别代入上式,得-4k+b=-9。解得一次函数的解析式为y=2x-1。设代解写 像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法. 在前面的学习过程中我们发现数与形之间是怎样结合互化的?函数解析式y=kx+b一次函数的图象直线l满足条件的两定点(x1,y1)(x2,y2)解出选取选取解出解题的四个步骤:第一步:设,设出函数的一般形式。(称一次函数的通式)第二步:代,代入解析式得出方程或方程组。第三步:解,通过列方程或方程组解出待定系数k,b的值。第四步:写,写出该函数的解析式。整理归纳从数到形从形到数数学的基本思想方法:数形结合练习:
(1)已知一次函数的图象经过点(1,-1)和点(-1,2)。求这个函数的解析式。
(2)已知一次函数y=kx+b中,当x=1时,y=3,当x=-1时,y=7。求这个函数的解析式。且求当x=3时,y的值。
(3)师:已知直线上两点坐标,能求出这条直线的解析式,若不直接告诉两点的坐标,已知这条直线的图象,能否求出它的解析式?
如:
1)已知一次函数的图象经过点(1,-1)和点(-1,2)。求这个函数的解析式。
解:设这个一次函数的解析式为y=kx+b。
把x=1,y=-1;x=-1,y=2,分别代入上式,得
﹛K+b=-1,
-k+b=2。
解得﹛K= ,b= 。一次函数的解析式为y= x 。(2)解:把x=1,y=3;x=-1,y=7,分别代入y=kx+b,得
﹛K+b=3,-k+b=7。解得﹛K=-2,b=5。一次函数的解析式为y=-2x+5。
当x=3时 ,y=-1。(3)由题意已知一次函数的图象经过点(2,0)和点(0,-3),设这个一次函数的解析为y=kx+b。
把x=2,y=0;x=0,y=-3分别代入上式,得
﹛2k+b=0,b=-3。解得﹛K= ,b=-3。一次函数的解析式为y= x-3。一次函数图像经过点(9,0)和点(24,20),写出函数解析式.解:练一练 设这个一次函数的解析式为y=kx+b.把点(9,0)与(24,20)分别代入y=kx+b,得:
已知一次函数的图象经过点(-4,9)和点(6,3),求这个函数的解析式.
解: 设这个一次函数的解析式为y=kx+b.把点(-4,9)与(6,3)分别代入y=kx+b,得:
练一练1、选择题CADD尝试练习3.一次函数y=kx+5与直线y=2x-1交于点P(2,m),求k、m的值.4.一次函数y=3x-b过A(-2,1)则b= ,该图象经过点B( ,-1)和点C(0, ).5.已知函数y=kx+b的图象与另一个一次函数y=-2x-1的图象相交于y轴上的点A,且x轴下方的一点B(3,n)在一次函数y=kx+b的图象上,n满足关系n2=9.求这个函数的解析式. 1.写出两个一次函数,使它们的图象都经过点(-2,3). 2.生物学家研究表明,某种蛇的长度y(cm)是其尾长x(cm)的一次函数,当蛇的尾长为6 cm时,蛇长为45.5 cm;当尾长为14 cm时,蛇长为105.5 cm.当蛇的尾长为10 cm时,这条蛇的长度是多少?四、综合应用y=7.5x+0.575.5 cm 3.一个函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,-3a)与点(a,6),求这个函数的解析式. 4.小明将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数x(月)之间的关系如图所示,根据下图回答下列问题: (1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经过几个月才能存够200元?O40xy123120804y=20x+408个月1.用待定系数法求函数解析式的一般步骤.2.数形结合解决问题的一般思路.五、回顾反思1.必做题:
教材第95页练习第1题,第99页习题19.2第6、7题.六、作业2.备选题: (1)若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过( )
A.A(-1,1) B.B(2,2)
C.C(-2,2) D.D(2,-2)
(2)老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质:
甲:函数的图象经过第一象限;
乙:函数的图象经过第二象限;
丙:在每个象限内,y随x的增大而减小.
请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数解析式: .
C (3)如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据: ①求出h与d之间的函数解析式(不要求写出自变量d的取值范围).
②某人身高为196 cm,一般情况下他的指距应是多少?解:(1)设h与d之间的函数关系式为:
h=kd+b. 把d=20,h=160,d=21,h=169,
分别代入得,
20k+b=160,
21k+b=169. 解得k=9,b=-20,
即h=9d-20. (2)当h=196时,196=9d-20,解得d=24(cm).再见!
