河北省满城中学2014-2015学年高一下学期第二次月考(期中)数学(文)试题
文档属性
| 名称 | 河北省满城中学2014-2015学年高一下学期第二次月考(期中)数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 346.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-30 00:00:00 | ||
图片预览



文档简介
2014—2015学年满城中学高一第二学期第二次月考
数学试题(文科生卷)
(时间120分钟,满分150分)
一、选择题:本大题共12小题,每小题5分。在每小题给出的四个选项中,只有一项是符合题目要求的。请把答案涂在客观题答题卡上。
1、已知三点在同一条直线上, 则的值为( )
、 、 、 、
2、设是不同的直线,是不重合的平面,则下列命题不正确的是( )
A、若,则 B、若,则
C、则
D、若且,则
3、已知是不同的直线,是不重合的平面,下列命题中正确的个数为( )
①若则 ②若则
③若则 ④则
、1 、2 、3 、4
4、若图,直线的斜率分别为,则( )
、 、
、 、
5、已知是不重合的平面,是不同的直线,则下列命题不正确的个数是( )
①若,则 ②若则
③若,则 ④若,则
、0 、1 、2 、3
6、设是不重合的平面,是不同的直线,下列命题不能推导出线面垂直的是( )
A.若,则 B.若,则
C.若,则
D.若,则
7、平面截球所得截面的面积为,球心到截面的距离为,此球的体积为( )
A、 B、 C、 D、
8、下列命题正确的是( )
①过平面外一点有且只有一条直线和已知平面垂直
②过直线外一点有且只有一个平面和已知直线垂直
③过平面外一点有且只有一条直线与已知平面平行
④过平面外一点有且只有一个平面与已知平面垂直
A.①②③?? B.①②???? ?C. ①④???? D.②③④
9、一个几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
10、直线经过点,且倾斜角范围是,
则的范围是( )
A、 B、
C、 D、
11、已知若平面内存在一点满足:且,则点坐标为( )
A、 B、 C、 D、
12、如图,网格纸上小正方形的边长为,粗实线画出的是某多面体的三视图,则
该多面体的各面中,面积最小的是( )
. . . .
二、填空题:本大题共4个小题,每小题5分。把答案填写在答题纸的相应位置。
13、直线经过点,则直线的倾斜角为 ;
14、已知为球的半径,过的中点且垂直于的平面截球面得到圆,若圆 的面积为,则球的表面积为____ ____;
15、已知三点,若过点的直线与线段总有公共点,则
直线的斜率的取值范围是 ;
16、如图是棱长为的正方体的平面展开图,则在原正方体中,
①平面; ②平面;
③CN与BM成角; ④DM与BN垂直.
以上四个命题中,正确命题的序号是____ ____。
(写出所有正确命题的序号)
三、解答题 :本大题共6个小题,合计 70分。解答应写出必要的文字说明和推理过程,
特别说明:立体几何题作辅助线时,要求在答题纸上先用铅笔画,再用碳素笔描。
17、(本小题满分10分)
已知线段的两个端点,直线,且直线的倾斜角为。求的值。
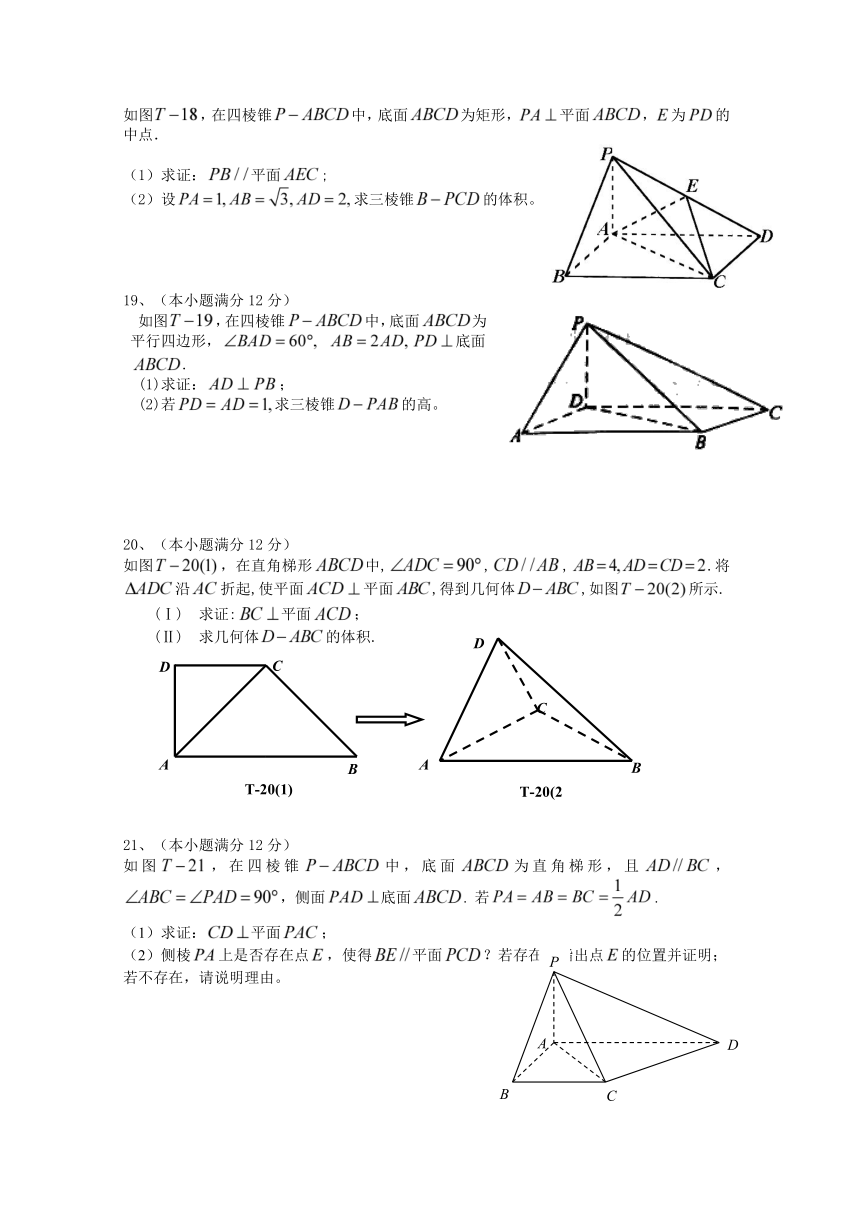
18、(本小题满分12分)
如图,在四棱锥中,底面为矩形,平面,为的中点.
(1)求证:平面;
(2)设求三棱锥的体积。
19、(本小题满分12分)
如图,在四棱锥中,底面为平行四边形, 底面.
(1)求证:;
(2)若求三棱锥的高。
20、(本小题满分12分)
如图,在直角梯形中,,,.将沿折起,使平面平面,得到几何体,如图所示.
(Ⅰ) 求证:平面;
(Ⅱ) 求几何体的体积.
21、(本小题满分12分)
如图,在四棱锥中,底面为直角梯形,且,,侧面底面. 若.
(1)求证:平面;
(2)侧棱上是否存在点,使得平面?若存在,指出点的位置并证明;
若不存在,请说明理由。
22、(本小题满分12分)
如图,在三棱柱中,侧面为菱形,
(1)求证:平面平面;
(2)若,,求四棱锥的体积。
2014—2015学年满城中学高一第二学期第二次月考
数学试题(文科生卷)
一、选择题:CDACBD CBCCAB
二、填空题: (也可以); ; ; .
三、解答题 :
17、(本小题满分10分)
解:∵直线的倾斜角为 ∴ ............................2分
∵ ∴ ..............................4分
∴ 即.解之得或. .................8分
经检验,时,与重合,不合题意,舍去。∴...............10分
18、(本小题满分12分)
(1)证明:连接,交于点,连接.
∵四边形为矩形
∴为的中点。
又∵为的中点.
∴.
∵平面,平面
∴平面 ..............................7分
(2)解:∵四边形为矩形,。
∴
∴ .................................12分
19、(本小题满分12分)
(1)证明:令则。
∵
∴
∴
即. ...........................3分
∵底面
∴
∵
∴底面.
∴. ..............................5分
(2)解:∵则。
过点作垂足为,连接。过点作垂足为
∵底面 ∴.
∵. ∴平面。
∴ ...............................9分
又∵
∴平面
∴线段的长就是三棱锥的高。
在中,由得
∵
∴
由得
∴三棱锥的高为。 ..................................12分
备注:等体积法酌情给分!
20、(本小题满分12分)
(1)证明:(法一)在直角梯形中,
∴, ∴ 即
∵平面底面,且交线为,平面
∴平面. ........................6分
(法二) 取的中点,连接.根据已知条件得.因此.
∵平面底面,且交线为,平面.
∴平面.
∴.
在直角梯形中,
∴, ∴ 即
∵
∴平面. ..........................6分
(2)解:在中,
由(1)可知平面,且则
∴
∴几何体的体积为 ..........................12分
21、(本小题满分12分)
证明:令则。
在直角梯形中,
∴, ∴ 即
又∵,∴
∵侧面底面,且交线为,平面
∴平面,
∵平面。 ........................6分
∴平面。
(2)解:存在侧棱的中点,使得平面。证明如下:
取的中点,的中点,连接可知
又 ∴
∴四边形为平行四边形。
∴ ∵平面,平面。
∴平面。
∴存在侧棱的中点,使得平面。. .......................12分
注:其他方法酌情给分。
22、(本小题满分12分)
(1)证明:∵四边形为菱形。
∴
∴平面
∴底面
∵平面.
∴平面平面 ..........................5分
(2)解:连接。
∵四边形为菱形。
∴为的中点。
∵
∴
在菱形中,
∴为等边三角形,
∴
∴即.
∵平面平面
∴面.
∴.
∴四棱锥的体积为。 ..........................12分
注:由底面得到,也可以得到面.
数学试题(文科生卷)
(时间120分钟,满分150分)
一、选择题:本大题共12小题,每小题5分。在每小题给出的四个选项中,只有一项是符合题目要求的。请把答案涂在客观题答题卡上。
1、已知三点在同一条直线上, 则的值为( )
、 、 、 、
2、设是不同的直线,是不重合的平面,则下列命题不正确的是( )
A、若,则 B、若,则
C、则
D、若且,则
3、已知是不同的直线,是不重合的平面,下列命题中正确的个数为( )
①若则 ②若则
③若则 ④则
、1 、2 、3 、4
4、若图,直线的斜率分别为,则( )
、 、
、 、
5、已知是不重合的平面,是不同的直线,则下列命题不正确的个数是( )
①若,则 ②若则
③若,则 ④若,则
、0 、1 、2 、3
6、设是不重合的平面,是不同的直线,下列命题不能推导出线面垂直的是( )
A.若,则 B.若,则
C.若,则
D.若,则
7、平面截球所得截面的面积为,球心到截面的距离为,此球的体积为( )
A、 B、 C、 D、
8、下列命题正确的是( )
①过平面外一点有且只有一条直线和已知平面垂直
②过直线外一点有且只有一个平面和已知直线垂直
③过平面外一点有且只有一条直线与已知平面平行
④过平面外一点有且只有一个平面与已知平面垂直
A.①②③?? B.①②???? ?C. ①④???? D.②③④
9、一个几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
10、直线经过点,且倾斜角范围是,
则的范围是( )
A、 B、
C、 D、
11、已知若平面内存在一点满足:且,则点坐标为( )
A、 B、 C、 D、
12、如图,网格纸上小正方形的边长为,粗实线画出的是某多面体的三视图,则
该多面体的各面中,面积最小的是( )
. . . .
二、填空题:本大题共4个小题,每小题5分。把答案填写在答题纸的相应位置。
13、直线经过点,则直线的倾斜角为 ;
14、已知为球的半径,过的中点且垂直于的平面截球面得到圆,若圆 的面积为,则球的表面积为____ ____;
15、已知三点,若过点的直线与线段总有公共点,则
直线的斜率的取值范围是 ;
16、如图是棱长为的正方体的平面展开图,则在原正方体中,
①平面; ②平面;
③CN与BM成角; ④DM与BN垂直.
以上四个命题中,正确命题的序号是____ ____。
(写出所有正确命题的序号)
三、解答题 :本大题共6个小题,合计 70分。解答应写出必要的文字说明和推理过程,
特别说明:立体几何题作辅助线时,要求在答题纸上先用铅笔画,再用碳素笔描。
17、(本小题满分10分)
已知线段的两个端点,直线,且直线的倾斜角为。求的值。
18、(本小题满分12分)
如图,在四棱锥中,底面为矩形,平面,为的中点.
(1)求证:平面;
(2)设求三棱锥的体积。
19、(本小题满分12分)
如图,在四棱锥中,底面为平行四边形, 底面.
(1)求证:;
(2)若求三棱锥的高。
20、(本小题满分12分)
如图,在直角梯形中,,,.将沿折起,使平面平面,得到几何体,如图所示.
(Ⅰ) 求证:平面;
(Ⅱ) 求几何体的体积.
21、(本小题满分12分)
如图,在四棱锥中,底面为直角梯形,且,,侧面底面. 若.
(1)求证:平面;
(2)侧棱上是否存在点,使得平面?若存在,指出点的位置并证明;
若不存在,请说明理由。
22、(本小题满分12分)
如图,在三棱柱中,侧面为菱形,
(1)求证:平面平面;
(2)若,,求四棱锥的体积。
2014—2015学年满城中学高一第二学期第二次月考
数学试题(文科生卷)
一、选择题:CDACBD CBCCAB
二、填空题: (也可以); ; ; .
三、解答题 :
17、(本小题满分10分)
解:∵直线的倾斜角为 ∴ ............................2分
∵ ∴ ..............................4分
∴ 即.解之得或. .................8分
经检验,时,与重合,不合题意,舍去。∴...............10分
18、(本小题满分12分)
(1)证明:连接,交于点,连接.
∵四边形为矩形
∴为的中点。
又∵为的中点.
∴.
∵平面,平面
∴平面 ..............................7分
(2)解:∵四边形为矩形,。
∴
∴ .................................12分
19、(本小题满分12分)
(1)证明:令则。
∵
∴
∴
即. ...........................3分
∵底面
∴
∵
∴底面.
∴. ..............................5分
(2)解:∵则。
过点作垂足为,连接。过点作垂足为
∵底面 ∴.
∵. ∴平面。
∴ ...............................9分
又∵
∴平面
∴线段的长就是三棱锥的高。
在中,由得
∵
∴
由得
∴三棱锥的高为。 ..................................12分
备注:等体积法酌情给分!
20、(本小题满分12分)
(1)证明:(法一)在直角梯形中,
∴, ∴ 即
∵平面底面,且交线为,平面
∴平面. ........................6分
(法二) 取的中点,连接.根据已知条件得.因此.
∵平面底面,且交线为,平面.
∴平面.
∴.
在直角梯形中,
∴, ∴ 即
∵
∴平面. ..........................6分
(2)解:在中,
由(1)可知平面,且则
∴
∴几何体的体积为 ..........................12分
21、(本小题满分12分)
证明:令则。
在直角梯形中,
∴, ∴ 即
又∵,∴
∵侧面底面,且交线为,平面
∴平面,
∵平面。 ........................6分
∴平面。
(2)解:存在侧棱的中点,使得平面。证明如下:
取的中点,的中点,连接可知
又 ∴
∴四边形为平行四边形。
∴ ∵平面,平面。
∴平面。
∴存在侧棱的中点,使得平面。. .......................12分
注:其他方法酌情给分。
22、(本小题满分12分)
(1)证明:∵四边形为菱形。
∴
∴平面
∴底面
∵平面.
∴平面平面 ..........................5分
(2)解:连接。
∵四边形为菱形。
∴为的中点。
∵
∴
在菱形中,
∴为等边三角形,
∴
∴即.
∵平面平面
∴面.
∴.
∴四棱锥的体积为。 ..........................12分
注:由底面得到,也可以得到面.
同课章节目录
